2019-2020学年八年级数学下册 第一部分 基础知识篇 第17课 归纳猜想型问题(B组)瞄准中考
- 格式:ppt
- 大小:426.00 KB
- 文档页数:13





八年级下册知识点归纳总结数学数学作为一门重要的学科,对于学生的学习和发展具有十分重要的作用。
八年级下册数学内容丰富,其中涵盖了许多重要的知识点。
为了帮助同学们更好地复习和总结这些知识点,下面对八年级下册的数学知识进行归纳总结。
一、代数与函数1. 初步认识函数(1)函数的概念:函数是一种特殊的关系。
(2)函数的表示方法:函数的三要素是输入、输出和对应关系,可以用表格、图象和公式等形式来表示函数。
(3)函数的性质:单调性、奇偶性、周期性等。
2. 一次函数(1)一次函数的概念:一次函数是指次数为1的函数。
(2)一次函数的性质:一次函数的图象是一条直线,可以通过两个点来确定一条一次函数。
(3)一次函数的表达式:函数的表达式通常为y=kx+b,其中k 和b为常数。
3. 二次函数(1)二次函数的概念:二次函数是指次数为2的函数。
(2)二次函数的性质:二次函数的图象是一个抛物线,可以通过顶点、对称轴和焦点等来确定二次函数。
(3)二次函数的表达式:函数的表达式通常为y=ax²+bx+c,其中a、b、c为常数。
4. 等差数列(1)等差数列的概念:等差数列是指数之间的差值相等的数列。
(2)等差数列的通项公式:通项公式为an=a1+(n-1)d,其中a1为首项,d为公差。
二、图形与尺度1. 平行线与三角形(1)平行线的判定:根据平行线的性质,可通过角的对应关系和直线之间的交错性质来判定平行线。
(2)三角形内部角的性质:三角形内部的角和为180°,其中等腰三角形、直角三角形有一些特殊的性质。
2. 四边形(1)四边形的分类:四边形可分为平行四边形、矩形、菱形、正方形等。
(2)四边形内角的性质:四边形的内角和为360°,不同类型的四边形有不同的内角性质。
3. 相似与全等(1)相似的概念:相似是指两个图形形状相同但大小可以不同。
(2)相似三角形的性质与判定:相似三角形的对应角相等,对应边成比例。




第十七章 勾股定理17.1 勾股定理1、勾股定理:如果直角三角形两直角边长分别为a 、b ,斜边长为c ,那么222a b c += 勾股定理的证明:方法一:4EFGH S S S ∆+=正方形正方形ABCD ,2214()2ab b a c ⨯+-=,化简可证.方法二:四个直角三角形的面积与小正方形面积的和等于大正方形的面积.四个直角三角形的面积与小正方形面积的和为221422S ab c ab c =⨯+=+大正方形面积为222()2S a b a ab b =+=++ ∴222a b c +=方法三:1()()2S a b a b =+⋅+梯形,2112S 222ADE ABE S S ab c ∆∆=+=⋅+梯形,化简得证17.2 勾股定理的逆定理2、勾股定理的逆定理:如果三角形的三边长a 、b 、c 满足222a b c +=,那么这个三角形是直角三角形.3、互逆命题的概念如果一个命题的题设和结论分别是另一个命题的结论和题设,这样的两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另一个叫做它的逆命题.4、勾股数:能够构成直角三角形的三边长的三个正整数称为勾股数,即222a b c +=中,a ,b ,c 为正整数时,称a ,b ,c 为一组勾股数常见的勾股数有:3、4、5;6、8、10;5、12、13;7、24、25等 例、在Rt △ABC 中,a=3,b=4,求c .错解由勾股定理,得bacbac cabcab cbaHG F EDCBAa bccbaE D CBA诊断这里默认了∠C为直角.其实,题目中没有明确哪个角为直角,当b>a时,∠B可以为直角,故本题解答遗漏了这一种情况.当∠B为直角时,例、已知Rt△ABC中,∠B=RT∠,,c= b.错解由勾股定理,得诊断这里错在盲目地套用勾股定理“a2+b2=c2”.殊不知,只有当∠C=Rt∠时,a2+b2=c2才能成立,而当∠B=Rt∠时,则勾股定理的表达式应为a2+c2=b2.正确解答∵∠B=Rt∠,由勾股定理知a2+c2=b2.∴例、若直角三角形的两条边长为6cm、8cm,则第三边长为________.错解设第三边长为xcm.由勾股定理,得x2=62+82.=10即第三边长为10cm.诊断这里在利用勾股定理计算时,误认为第三边为斜边,其实题设中并没有说明已知的两边为直角边,∴第三边可能是斜边,也可能是直角边.正确解法设第三边长为xcm.若第三边长为斜边,由勾股定理,得=10(cm)若第三边长为直角边,则8cm长的边必为斜边,由勾股定理,得=(cm)因此,第三边的长度是10cm或者例、如图,已知Rt △ABC 中,∠BAC=90°,AD 是高,AM 是中线,且AM=12BC=233AD.又RT △ABC的周长是(6+23)cm.求AD .错解 ∵△ABC 是直角三角形, ∴AC:AB:BC=3:4:5 ∴AC ∶AB ∶BC=3∶4∶5.∴AC=312(6+23)=332+,AB=412(6+23)=6233+,BC=512(6+23)=15536+又∵12AC AB •=12BC AD • ∴AD=AC AB BC •=336232315536++⨯+ =(33)2(33)5(33)+•++=25(3+3)(cm) 诊断 我们知道,“勾三股四弦五”是直角三角形中三边关系的一种特殊情形,并不能代表一般的直角三角形的三边关系.上述解法犯了以特殊代替一般的错误.正确解法∵AM=233AD ∴MD=222(3)3AD AD -=33AD 又∵MC=MA ,∴CD=MD . ∵点C 与点M 关于AD 成轴对称. ∴AC=AM ,∴∠AMD=60°=∠C .∴∠B=30°,AC=12BC ,AB=32BC∴AC+AB+BC=12BC+32BC+BC=6+23.∴BC=4.∵12BC=233AD,∴AD=12233BC=3(cm)例、在△ABC中,a∶b∶c=9∶15∶12,试判定△ABC是不是直角三角形.错解依题意,设a=9k,b=15k,c=12k(k>0).∵a2+b2=(9k)2+(15k)2=306k2,c2=(12k)2=144k2,∴a2+b2≠c2.∴△ABC不是直角三角形.诊断我们知道“如果一个三角形最长边的平方等于另外两边的平方和,那么这个三角形是直角三角形”.而上面解答错在没有分辨清楚最长边的情况下,就盲目套用勾股定理的逆定理.正确解法由题意知b是最长边.设a=9k,b=15k,c=12k(k>0).∵a2+c2=(9k)2+(12k)2=81k2+144k2=225k2.b2=(15k)2=225k2,∴a2+c2=b2.∴△ABC是直角三角形.例、已知在△ABC中,AB>AC,AD是中线,AE是高.求证:AB2-AC2=2BC·DE错证如图.∵AE⊥BC于E,∴AB2=BE2+AE2,AC2=EC2+AE2.∴AB2-AC2=BE2-EC2=(BE+EC)·(BE-EC)=BC·(BE-EC).∵BD=DC,∴BE=BC-EC=2DC-EC.∴AB2-AC2=BC·(2DC-EC-EC)=2BC·DE.诊断题设中既没明确指出△ABC的形状,又没给出图形,因此,这个三角形有可能是锐角三角形,也可能是直角三角形或钝角三角形.∴高AE既可以在形内,也可以与一边重合,还可以在形外,这三种情况都符合题意.而这里仅只证明了其中的一种情况,这就犯了以偏概全的错误.剩下的两种情况如图所示.正确证明由读者自己完成.例、已知在△ABC中,三条边长分别为a,b,c,a=n,b=24n-1,c=244n+(n是大于2的偶数).求证:△ABC是直角三角形.错证1∵n是大于2的偶数,∴取n=4,这时a=4,b=3,c=5.∵a2+b2=42+32=25=52=c2,∴△ABC是直角三角形(勾股定理的逆定理).由勾股定理知△ABC是直角三角形.正解∵a2+b2=n2+(24n-1)2=n2+416n-22n+1=416n+22n+1c2=(244n+)2=(214n+)2=416n+22n+1由勾股定理的逆定理知,△ABC是直角三角形. 诊断证明1错在以特殊取代一般.。

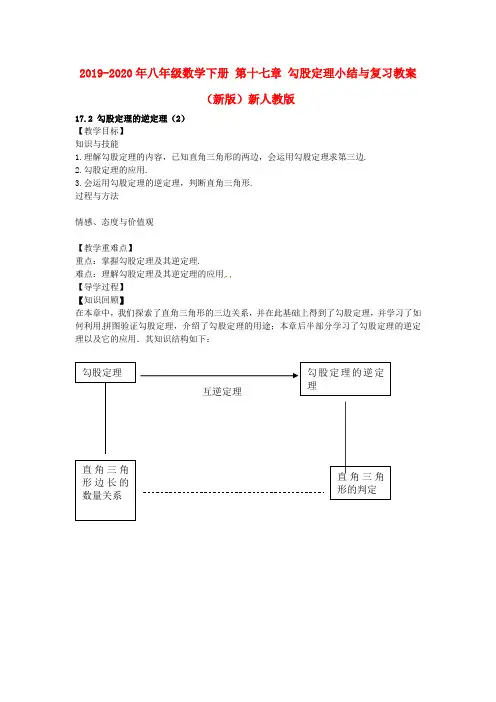
2019-2020年八年级数学下册第十七章勾股定理小结与复习教案(新版)新人教版17.2 勾股定理的逆定理(2)【教学目标】知识与技能1.理解勾股定理的内容,已知直角三角形的两边,会运用勾股定理求第三边.2.勾股定理的应用.3.会运用勾股定理的逆定理,判断直角三角形.过程与方法情感、态度与价值观【教学重难点】重点:掌握勾股定理及其逆定理.难点:理解勾股定理及其逆定理的应用.【导学过程】【知识回顾】在本章中,我们探索了直角三角形的三边关系,并在此基础上得到了勾股定理,并学习了如何利用拼图验证勾股定理,介绍了勾股定理的用途;本章后半部分学习了勾股定理的逆定理以及它的应用.其知识结构如下:1.勾股定理:(1)直角三角形两直角边的______和等于_______的平方.就是说,对于任意的直角三角形,如果它的两条直角边分别为a 、b ,斜边为c ,那么一定有:————————————.这就是勾股定理.(2)勾股定理揭示了直角三角形___之间的数量关系,是解决有关线段计算问题的重要依据. 22222222,,b a c a c b b c a +=-=-=,2222,a c b b c a -=-=.勾股定理的探索与验证,一般采用“构造法”.通过构造几何图形,并计算图形面积得出一个等式,从而得出或验证勾股定理.2.勾股定理逆定理“若三角形的两条边的平方和等于第三边的平方,则这个三角形为________.”这一命题是勾股定理的逆定理.它可以帮助我们判断三角形的形状.为根据边的关系解决角的有关问题提供了新的方法.定理的证明采用了构造法.利用已知三角形的边a,b,c(a 2+b 2=c 2),先构造一个直角边为a,b 的直角三角形,由勾股定理证明第三边为c,进而通过“SSS ”证明两个三角形全等,证明定理成立.3.勾股定理的作用:(1)已知直角三角形的两边,求第三边;(2)在数轴上作出表示n (n 为正整数)的点. 勾股定理的逆定理是用来判定一个三角形是否是直角三角形的.勾股定理的逆定理也可用来证明两直线是否垂直,勾股定理是直角三角形的性质定理,而勾股定理的逆定理是直角三角形的判定定理,它不仅可以判定三角形是否为直角三角形,还可以判定哪一个角是直角,从而产生了证明两直线互相垂直的新方法:利用勾股定理的逆定理,通过计算来证明,体现了数形结合的思想.(3)三角形的三边分别为a 、b 、c ,其中c 为最大边,若222c b a =+,则三角形是直角三角形;若222c b a >+,则三角形是锐角三角形;若2<+c b a 22,则三角形是钝角三角形.所以使用勾股定理的逆定理时首先要确定三角形的最大边.【经典例题】探究一、探究二、探究三、…….【知识梳理】【随堂练习】1:如果一个直角三角形的两条边长分别是6cm 和8cm ,那么这个三角形的周长和面积分别是多少?2:如图,在四边形ABCD 中,∠C=90°,AB=13,BC=4,CD=3,AD=12,求证:AD ⊥BD .1.如果下列各组数是三角形的三边,那么不能组成直角三角形的一组数是( )A .7,24,25B .321,421,521C .3,4,5D .4,721,821 2.如果把直角三角形的两条直角边同时扩大到原来的2倍,那么斜边扩大到原来的( )A .1倍B .2倍C .3倍D .4倍 3.三个正方形的面积如图1,正方形A 的面积为( )A . 6B . 36C . 64D . 8 4.直角三角形的两直角边分别为5cm ,12cm ,其中斜边上的高为( ) A .6cm B .8.5cm C .1330cm D .1360cm 5.在△ABC 中,三条边的长分别为a ,b ,c ,a =n 2-1,b =2n ,c =n 2+1(n >1,且为整数),这个三角形是直角三角形吗?若是,哪个角是直角。
勾股定理全章知识点归纳及典型题分类一.基础知识点: 1:勾股定理直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
(即:a 2+b 2=c 2) 要点诠释:勾股定理反映了直角三角形三边之间的关系,是直角三角形的重要性质之一,其主要应用:(1)已知直角三角形的两边求第三边(在ABC ∆中,90C ∠=︒,则c,b,a )(2)已知直角三角形的一边与另两边的关系,求直角三角形的另两边(3)利用勾股定理可以证明线段平方关系的问题 2:勾股定理的逆定理如果三角形的三边长:a 、b 、c ,则有关系a 2+b 2=c 2,那么这个三角形是直角三角形。
要点诠释:勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时应注意: (1)首先确定最大边,不妨设最长边长为:c ;(2)验证c 2与a 2+b 2是否具有相等关系,若c 2=a 2+b 2,则△ABC 是以∠C 为直角的直角三角形(若c 2>a 2+b 2,则△ABC 是以∠C 为钝角的钝角三角形;若c 2<a 2+b 2,则△ABC 为锐角三角形)。
(定理中a ,b ,c 及222a b c +=只是一种表现形式,不可认为是唯一的,如若三角形三边长a ,b ,c 满足222a c b +=,那么以a ,b ,c 为三边的三角形是直角三角形,但是b 为斜边)3:勾股定理与勾股定理逆定理的区别与联系区别:勾股定理是直角三角形的性质定理,而其逆定理是判定定理;联系:勾股定理与其逆定理的题设和结论正好相反,都与直角三角形有关。
4:互逆命题的概念如果一个命题的题设和结论分别是另一个命题的结论和题设,这样的两个命题叫做互逆命题。
如果把其中一个叫做原命题,那么另一个叫做它的逆命题。
5:勾股定理的证明勾股定理的证明方法很多,常见的是拼图的方法 用拼图的方法验证勾股定理的思路是①图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变 ②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理 6:勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数,即222a b c +=中,a ,b ,c 为正整数时,称a ,b ,c 为一组勾股数②记住常见的勾股数可以提高解题速度,如3,4,5;6,8,10;5,12,13;7,24,25等③用含字母的代数式表示n 组勾股数:221,2,1n n n -+(2,n ≥n 为正整数); 2221,22,221n n n n n ++++(n 为正整数)2222,2,m n mn m n -+(,m n >m ,n为正整数) 二、典型题归类 类型一:等面积法求高【例题】如图,△ABC 中,∠ACB=900,AC=7,BC=24,C D ⊥AB 于D 。
2019年人教版数学初二下学期第十七章知识点总结第十七章 勾股定理1.勾股定理:如果直角三角形的两直角边长分别为a ,b ,斜边长为c ,那么a 2+b 2=c 2。
2.勾股定理逆定理:如果三角形三边长a,b,c 满足a 2+b 2=c 2。
,那么这个三角形是直角三角形。
3.经过证明被确认正确的命题叫做定理。
我们把题设、结论正好相反的两个命题叫做互逆命题。
如果把其中一个叫做原命题,那么另一个叫做它的逆命题。
(例:勾股定理与勾股定理逆定理)4.直角三角形的性质(1)、直角三角形的两个锐角互余。
可表示如下:∠C=90°⇒∠A+∠B=90°(2)、在直角三角形中,30°角所对的直角边等于斜边的一半。
∠A=30°可表示如下: ⇒BC=21AB ∠C=90°(3)、直角三角形斜边上的中线等于斜边的一半∠ACB=90°可表示如下: ⇒CD=21AB=BD=AD D 为AB 的中点5、摄影定理 在直角三角形中,斜边上的高线是两直角边在斜边上的摄影的比例中项,每条直角边是它们在斜边上的摄影和斜边的比例中项∠ACB=90° BD AD CD •=2⇒ AB AD AC •=2CD ⊥AB AB BD BC •=26、常用关系式由三角形面积公式可得:AB •CD=AC •BC7、直角三角形的判定1、有一个角是直角的三角形是直角三角形。
2、如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
3、勾股定理的逆定理:如果三角形的三边长a ,b ,c 有关系222c b a =+,那么这个三角形是直角三角形。
8、命题、定理、证明1、命题的概念判断一件事情的语句,叫做命题。
理解:命题的定义包括两层含义:(1)命题必须是个完整的句子;(2)这个句子必须对某件事情做出判断。
2、命题的分类(按正确、错误与否分)真命题(正确的命题)命题假命题(错误的命题)所谓正确的命题就是:如果题设成立,那么结论一定成立的命题。