-动力学方程的建立实例

高质量的文章撰写需要精细的研究和深入的思考，以下是一篇对于二连杆机械臂的拉格朗日动力学推导式的文章：1. 介绍二连杆机械臂是工业自动化中常见的一种机械结构，其运动特点复杂，控制困难。

为了对二连杆机械臂的运动进行有效的控制和分析，需要建立其动力学模型。

拉格朗日方法是一种描述系统动力学行为的有效方法，本文将使用拉格朗日方法推导二连杆机械臂的动力学方程。

2. 机械臂建模为了推导二连杆机械臂的动力学方程，首先需要对机械臂进行建模。

假设两个连杆的长度分别为l1和l2，质量分别为m1和m2，重心到旋转轴的距离分别为r1和r2，角度分别为θ1和θ2，推导用于描述系统的广义坐标和广义速度。

3. 拉格朗日动力学一般来说，拉格朗日方程可以表示为T-V=Q，其中T为系统的动能，V为系统的势能，Q为系统的外力。

首先计算系统的动能和势能，进而得到系统的拉格朗日方程。

4. 系统的动能对于二连杆机械臂而言，系统的动能包括了两个连杆的动能以及它们之间的相对动能。

根据运动学关系和动能的定义，可以得到系统的动能表达式。

5. 系统的势能与系统的动能类似，系统的势能也需要考虑两个连杆的势能以及它们之间的相对势能。

根据重力势能的定义和相对位置关系，可以得到系统的势能表达式。

6. 系统的拉格朗日方程将系统的动能和势能代入拉格朗日方程中，可以得到描述系统动力学行为的拉格朗日方程。

在此过程中，需要注意计算各项的偏导，并且考虑到其中一些项可能是不显式的。

7. 系统的控制通过建立系统的动力学方程，可以对二连杆机械臂的控制进行分析和设计。

可以通过对拉格朗日方程进行求解，得到系统的运动方程，并设计合适的控制器实现对机械臂的控制。

8. 结论通过本文对二连杆机械臂的拉格朗日动力学推导式的分析，可以得到系统的动力学方程，这对于机械臂的控制和设计具有重要意义。

在未来的研究和应用中，可以在此基础上进行更深入的分析和探索。

总结：本文通过拉格朗日动力学的方法推导了二连杆机械臂的动力学方程，这为机械臂的控制和设计提供了重要的理论基础。

动力学中的动力学方程如何建立和求解物体的动力学方程动力学方程是描述物体运动状态变化的数学表达式，它是动力学研究的基础和核心。

本文将介绍动力学方程的建立和求解方法。

一、动力学方程的建立物体的动力学方程基于牛顿第二定律，根据物体所受的外力和运动状态的关系来描述物体的运动过程。

根据牛顿第二定律的表达式：F =m · a，其中F是物体所受的合外力，m是物体的质量，a是物体的加速度。

在建立动力学方程时，首先需要确定物体所受的合外力，包括重力、摩擦力、弹力等。

将这些力的合力代入牛顿第二定律的表达式中，即可得到物体的动力学方程。

以一个简单的例子来说明动力学方程的建立过程。

假设有一个质量为m的物体在水平面上受到一个恒定的外力F，摩擦系数为μ。

可以得到物体所受的合外力为：F - μmg = ma，其中，g是重力加速度。

根据上述方程可以求解物体的运动状态，进而揭示其运动规律。

但是，在实际情况下，动力学方程可能会比较复杂，需要采用数值方法或近似方法进行求解。

二、求解物体的动力学方程物体的动力学方程可以通过解析方法或数值方法来求解。

1. 解析方法解析方法是通过数学手段求得方程的解析解，即得到物体的运动规律的具体表达式。

这种方法适用于动力学方程较简单的情况，或具有某些特定形式的外力作用下。

例如，一个质量为m的物体，沿着带有弹性系数k的弹簧直线运动，受到外力F的作用。

可以求解得到物体的位移随时间的变化规律：mx'' + kx = F，其中，x为物体的位移，t为时间。

通过解方程，可以得到物体受力情况下的运动规律。

2. 数值方法对于复杂的动力学方程，通常采用数值方法进行求解。

数值方法通过将时间和位移分段离散化，将连续的动力学问题转化为离散的数值计算问题。

常用的数值方法有欧拉法、改进的欧拉法和龙格-库塔法等。

这些方法通过计算每个离散时间间隔的物体状态，逐步求解动力学方程，并获得物体的运动轨迹。

数值方法的优势在于它们可以处理非线性和复杂的动力学方程，适用于各种实际情况下的物体运动问题。

常用的建立机器人动力学方程的方法在机器人领域，动力学方程的建立是至关重要的。

它不仅能够描述机器人的运动状态，还能为控制算法提供依据。

下面，我们以一个简单的双轮机器人为例，探讨常用的建立机器人动力学方程的方法。

首先，我们请来我们的“机器人设计师”小张，他告诉我们：“建立动力学方程，首先要明确所研究的机器人系统的结构。

对于双轮机器人，我们主要关注其重心运动和轮子的滚动运动。

”接下来，我们请来“机器人力学专家”小李，他补充说：“建立动力学方程，通常采用拉格朗日方法和牛顿-欧拉方法。

下面，我就分别介绍一下这两种方法。

”小李继续说道：“拉格朗日方法是一种基于能量守恒原理的方法。

首先，我们要确定机器人系统的动能和势能。

对于双轮机器人，其动能主要来自于轮子的滚动和机器人的平移，势能主要来自于机器人的重力势能。

然后，我们根据能量守恒原理，列出拉格朗日方程。

对于双轮机器人，其拉格朗日方程可以表示为：L = T - V，其中L为拉格朗日函数，T为动能，V为势能。

”“那牛顿-欧拉方法呢？”小张好奇地问。

小李微笑着回答：“牛顿-欧拉方法是一种基于牛顿运动定律的方法。

它通过分析机器人各关节的运动，建立动力学方程。

对于双轮机器人，我们可以分别研究其轮子、机器人和地面的运动。

首先，我们确定各部分的运动方程，然后通过牛顿运动定律将它们联立起来。

对于双轮机器人，其牛顿-欧拉方程可以表示为：Mq''(t) + Cq'(t) +Kg(t) = τ(t)，其中M为质量矩阵，q''(t)为加速度向量，C为阻尼矩阵，q'(t)为速度向量，K为刚度矩阵，g(t)为广义重力向量，τ(t)为广义力向量。

”“听起来好复杂啊！”小张感慨地说。

小李笑着回答：“确实如此，但只要掌握好基本原理，建立动力学方程也不是那么困难。

此外，我们还可以借助计算机辅助设计软件来简化计算过程。

”经过一番探讨，我们终于明白了常用的建立机器人动力学方程的方法。

系统动力学模型介绍1.系统动力学的思想、方法系统动力学对实际系统的构模和模拟是从系统的结构和功能两方面同时进行的。

系统的结构是指系统所包含的各单元以及各单元之间的相互作用与相互关系。

而系统的功能是指系统中各单元本身及各单元之间相互作用的秩序、结构和功能，分别表征了系统的组织和系统的行为，它们是相对独立的，又可以在—定条件下互相转化。

所以在系统模拟时既要考虑到系统结构方面的要素又要考虑到系统功能方面的因素，才能比较准确地反映出实际系统的基本规律。

系统动力学方法从构造系统最基本的微观结构入手构造系统模型。

其中不仅要从功能方面考察模型的行为特性与实际系统中测量到的系统变量的各数据、图表的吻合程度，而且还要从结构方面考察模型中各单元相互联系和相互作用关系与实际系统结构的一致程度。

模拟过程中所需的系统功能方面的信息，可以通过收集，分析系统的历史数据资料来获得，是属定量方面的信息，而所需的系统结构方面的信息则依赖于模型构造者对实际系统运动机制的认识和理解程度，其中也包含着大量的实际工作经验，是属定性方面的信息。

因此，系统动力学对系统的结构和功能同时模拟的方法，实质上就是充分利用了实际系统定性和定量两方面的信息，并将它们有机地融合在一起，合理有效地构造出能较好地反映实际系统的模型。

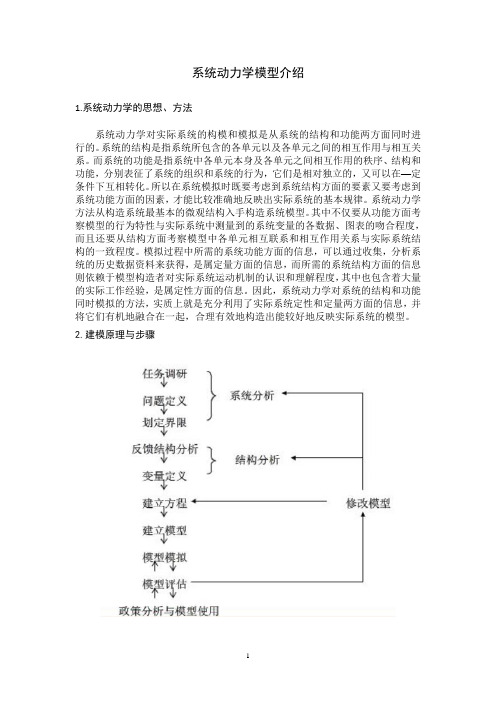
2.建模原理与步骤(1)建模原理用系统动力学方法进行建模最根本的指导思想就是系统动力学的系统观和方法论。

系统动力学认为系统具有整体性、相关性、等级性和相似性。

系统内部的反馈结构和机制决定了系统的行为特性，任何复杂的大系统都可以由多个系统最基本的信息反馈回路按某种方式联结而成。

系统动力学模型的系统目标就是针对实际应用情况，从变化和发展的角度去解决系统问题。

系统动力学构模和模拟的一个最主要的特点，就是实现结构和功能的双模拟，因此系统分解与系统综合原则的正确贯彻必须贯穿于系统构模、模拟与测试的整个过程中。

与其它模型一样，系统动力学模型也只是实际系统某些本质特征的简化和代表，而不是原原本本地翻译或复制。

能量守恒建立动力学方程
能量守恒原理是物理学中的一个基本原理，它指出在一个封闭系统内，能量总量是不变的。

能量可以从一种形式转换为另一种形式，但总能量始终保持不变，这是物理学中所说的能量守恒。

在动力学中，能量守恒原理是非常重要的。

动力学是研究物体运动的学科，它描述了物体的运动状态如何随时间而变化。

能量守恒原理可以被用来建立动力学方程，这些方程可以描述物体在运动中的能量变化。

以一个简单的例子来说明。

假设一个小球从一定高度自由落体，重力作用下它的动能将不断增加，而势能将不断减少。

根据能量守恒原理，球的总能量保持不变，因此动能和势能的减少总和等于总能量减少的量。

我们可以用数学方式来表示这个过程。

设小球的质量为m，高度为h，则小球的势能为mgh，其中g是重力加速度。

当球下落到高度h1时，它的势能为mgh1，动能为0。

当球下落到高度h2时，它的势能为mgh2，动能为(mv^2)/2，其中v是球的速度。

因此，球在下落的过程中，能量守恒原理可以表示为：
mgh1 = (mv^2)/2 + mgh2
这就是动力学方程，它描述了小球在下落过程中速度和高度如何随时间而变化。

这个方程可以用来计算球下落的速度和高度，以及球的动能和势能在不同高度下的大小。

总之，能量守恒原理是动力学中非常重要的概念，它可以被用来
建立动力学方程，描述物体在运动中的能量变化，从而帮助我们更好地理解物体的运动状态。

欧拉拉格朗日方法建立动力学方程下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢！本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注！Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!欧拉拉格朗日方法建立动力学方程动力学是研究物体运动规律的重要分支，而欧拉拉格朗日方法是解决动力学问题的一种强大工具。

化学反应动力学的数学模型建立化学反应动力学研究了化学反应的速率与反应条件、反应物浓度以及温度等因素之间的关系。

为了更好地理解和预测化学反应的行为，科学家们发展了各种数学模型来描述化学反应的动力学过程。

本文将介绍一些常见的化学反应动力学的数学模型以及它们的建立方法。

一、零阶反应动力学模型在零阶反应中，反应速率与反应物的浓度无关，即反应速率恒定。

这种反应动力学可以用一个简单的线性方程来描述：r = -k其中，r是反应速率，k是反应速率常数。

由于反应速率与反应物的浓度无关，因此反应速率始终保持不变。

二、一阶反应动力学模型一阶反应动力学是一种常见的反应类型，它的反应速率与反应物浓度成正比。

一阶反应的数学模型可以表示为：r = -k[A]其中，r为反应速率，k为反应速率常数，[A]为反应物A的浓度。

该方程反映了反应速率与反应物浓度之间的线性关系。

三、二阶反应动力学模型二阶反应是指反应速率与反应物浓度的平方成正比。

二阶反应的数学模型可以表示为：r = -k[A]^2其中，r为反应速率，k为反应速率常数，[A]为反应物A的浓度。

与一阶反应不同，二阶反应速率与反应物浓度的平方呈线性关系。

四、阿伦尼乌斯方程阿伦尼乌斯方程是一种综合考虑了反应物浓度和温度对反应速率影响的动力学模型。

该方程可以表示为：r = k[A]^m[B]^n * exp(-Ea/RT)其中，r为反应速率，k为反应速率常数，[A]和[B]分别为反应物A 和B的浓度，m和n为反应物的反应级别，Ea为活化能，R为气体常数，T为反应温度。

阿伦尼乌斯方程考虑了反应物浓度的影响以及温度对反应速率的影响，可以更准确地描述复杂的化学反应动力学过程。

五、科斯塔方程科斯塔方程是描述液相化学反应动力学的一种常用模型。

该方程可以表示为：r = k[C]/(1 + k'[C])其中，r为反应速率，k和k'为反应速率常数，[C]为反应物C的浓度。

科斯塔方程考虑了反应物浓度对反应速率的影响，并引入了两个反应速率常数以更好地拟合实验数据。