江苏省无锡市前洲中学苏科版七年级数学上册学案（无答案）：62角（2）

课题学习内容订正栏学习目标1．了解角平分线，并能够画出一个角的平分线；2．用量角器和直尺画一个角等于已知角的基础上，能够用圆规和直尺画一个角等于已知角；3．能够运用角平分线的知识，求简单的角的度数.一、课前预习1．利用一副三角板除了可直接作出30°、45°、60°和90°的角之外,还可以作出一些特殊的角,右图中作出的∠ABC的度数为A.55°B.65°C.75°D.105°思考：用一副三角板，可以画出多少种不同的角？2．画出∠AOB的角平分线.总结：从一个角的____点引出的一条____线，把这个角分成两个________的角，这条射线叫做这个角的________。

3．射线OC是∠AOB的角平分线，那么∠AOB、∠AOC、∠BOC之间有怎样的关系？二．合作探究例1. 已知︒=∠60AOB，其角平分线为OM，︒=∠20BOC，其角平分线为ON，则MON∠的大小为多少度？（自己画图）AB C例 2.如图，从平角POQ ∠的顶点出发画一条射线OB ，OC OA 、分别是BOP QOB ∠∠、的角平分线，求AOC ∠的度数.三．达标检测1.如图，_____________________++=∠AOB ，_____________________________-=+=∠AOD2.利用一副三角板上已知度数的角,不能画出的角是（ ）A .15°B .135°C .165°D .100°3.如图,∠COD 为平角,AO ⊥OE ,∠AOC = 2∠DOE ,则有∠AOC =____________.4.如图，直线a 、b 的夹角为90°,∠1=50°,则∠2=____________.5.如图，将书页斜折过去，使角的顶点A 落在F 处，BC 为折痕，BD 为EBF ∠的平分线，求CBD ∠的度数。

苏科版数学七年级上册6.2 角教教学设计一. 教材分析苏科版数学七年级上册6.2节主要介绍角的概念。

学生通过学习角的定义、分类（锐角、直角、钝角、周角）以及角的度量，进一步理解几何图形之间的关系。

本节课的内容是学生学习几何的基础，对于培养学生的空间观念和逻辑思维能力具有重要意义。

二. 学情分析七年级的学生已经掌握了初步的数学知识，具备一定的观察、思考和动手操作能力。

但部分学生对抽象的几何概念理解起来较为困难，因此，在教学过程中要注重引导学生通过实际操作来理解角的概念。

三. 教学目标1.知识与技能：掌握角的定义、分类，学会用度量工具测量角的大小。

2.过程与方法：通过观察、操作、交流等活动，培养学生的空间观念和逻辑思维能力。

3.情感态度与价值观：激发学生对数学的兴趣，培养合作意识，感受数学与生活的联系。

四. 教学重难点1.重点：角的定义、分类及度量。

2.难点：理解角的分类，学会用度量工具测量角的大小。

五. 教学方法采用“情境教学法”、“问题驱动法”和“合作学习法”等，引导学生主动探究，合作交流，培养学生的动手操作能力和思维能力。

六. 教学准备1.教具：直尺、量角器、三角板等。

2.学具：每人一套几何画板，用于操作和绘制图形。

七. 教学过程1.导入（5分钟）教师通过提问方式引导学生回顾以前学过的线段、射线等知识，为新课的学习做好铺垫。

接着，利用教具（如三角板）展示各种角，引发学生对角的兴趣。

2.呈现（10分钟）教师通过几何画板展示各种角，引导学生观察、思考，总结角的特征。

然后，介绍角的定义、分类及度量方法。

3.操练（10分钟）学生分组进行实践活动，使用几何画板和量角器测量各种角的大小，巩固对角的理解。

教师巡回指导，解答学生疑问。

4.巩固（10分钟）教师出示一些练习题，学生独立完成，检查对角的概念、分类和度量的掌握情况。

互相交流，巩固所学知识。

5.拓展（10分钟）教师引导学生思考：角在实际生活中的应用。

学生举例说明，如钟表、自行车等。

课 题：6．2角（2）姓名【学习目标】1．会利用三角板、量角器、圆规和直尺等画图工具画一个角等于已知角； 2．能画一个角的角平分线，并能了解角平分线的性质和方位角的表示． 【学习重点】明白得角平分线的意义,方位角的意义．【问题导学】问题1．如图，已知∠AOB，求作：∠A'O'B'，使∠A'O'B'=∠AOB．按要求画图： 作法：(1) 画射线O'A'．(2) 以点O 为圆心，以适当长为半径画弧，交OA 与C ，交OB 于D ． (3) 以点O'为圆心，以OC 长为半径画弧，交O'A'于C'． (4) 以点C'为圆心，以CD 长为半径圆弧，交前一条弧于D'． (5) 通过点D'画射线O'B'．∠A'O'B'即为所求的角．问题2．方位角以南北为基准，不以东西为基准．如“北偏东60°，南偏西50°．”等．偏45°时，说成“东南、西南、东北或西北方向”实践：如图（上左）：射线OA 表示方向 ；OA 的反向延长线表示 方向； 画表示南偏东30°方向的射线OC ； 画表示西北方向的射线OD问题3．阅读讲义P155．如图，OC 将∠AOB 分成相等的两部份，OC 确实是∠AOB 的角平分线． ∠AOC=∠ =21∠ ，或∠AOB=2∠ =2∠ ．问题1作图区西东AO【问题探讨】问题1．(1) 某测绘装置上一枚指针原先指向南偏西55︒,把这枚指针按逆时针方向旋转80︒, 那么结果指针的指向 ( ) A ．南偏东35º B．北偏西35º C．南偏东25º D．北偏西25º (2)8时30分时，钟表的时针与分针的夹角是多少度？问题2．如图，∠AOB=35°，∠BOC=50°，∠COD=21°，OE 平分∠AOD,求∠BOE 的度数．问题3．已知：一副三角板由一个等腰三角形和一个含30°角的直角三角形组成, 利用这副三角板组成15°角的方式很多,请你画出其中三种不同组成的示用意,并在图上作出必要的标注,不写作法．【问题评判】1．如图，三条直线AB ，CD ，EF 相交于O ，假设∠AOD=3∠FOD，∠AOE=120°，那么∠EOC 的度数为（ ） A ．30° B．40° C．20° D．15°FOED C B AAB D E F C3124 ODB CA（第1题图） （第2题图） （第3题图）2．如图，∠1=∠2，∠3=∠4，那么以下结论正确的个数为（）①AD平分∠BAF；②AF平分∠BAC；③AE平分∠DAF；④AF平分∠DAC；⑤AE平分∠BAC；A．4 B．3 C．2 D．13．如图，∠AOB=∠COD=90o，∠BOC=7∠BOD，那么∠BOD的度数为（）A．10° B．15° C．20° D．25°4．在海上，灯塔位于一艘船的北偏东40°方向，那么这艘船位于那个灯塔的（）A．南偏西50°方向 B．南偏西40°方向 C．北偏东50°方向 D．北偏东40°方向5．已知∠AOB=3∠BOC,假设∠BOC=30°，那么∠AOC等于_____________．6．如图，OM平分∠AOB，ON平分∠COD，假设∠MON=50°，∠BOC=10°，求∠AOD的度数．O DBCANM。

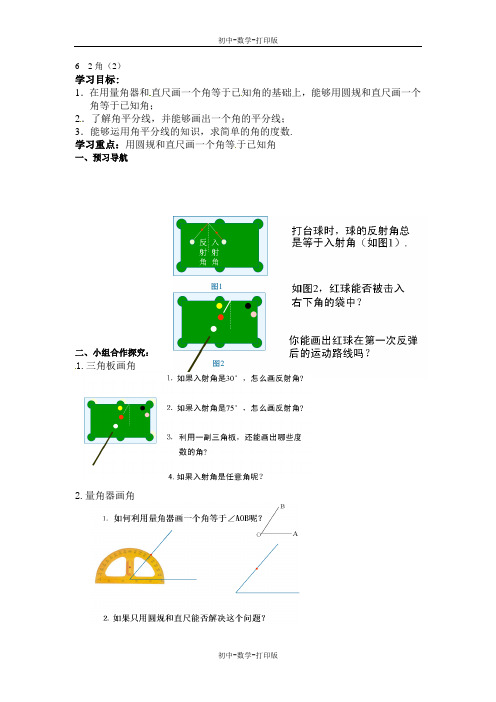
6 2角（2）学习目标:1．在用量角器和直尺画一个角等于已知角的基础上，能够用圆规和直尺画一个角等于已知角；2．了解角平分线，并能够画出一个角的平分线；3．能够运用角平分线的知识，求简单的角的度数.学习重点：用圆规和直尺画一个角等于已知角一、预习导航二、小组合作探究：1.三角板画角2.量角器画角3.尺规画角（1）明确探索关键.（2）“点”的确定.4.尺规作图总结5.角平分线定义6.∠AOC, ∠BOC, ∠AOB 这间有什么关系？7如图，如果∠AOD=80°，OC 是∠ AOD 内的一条射线，OB 是∠AOC 的平分线，∠AOB=30°.求∠AOC 与∠COD 的度数.三、自我总结，提出质疑：四、巩固拓展：1、 从一个角的____点引出的一条____线，把这个角分成两个________的角，这条射线叫做这个角的________。

如图，∵OC 平分AOB ∠，∴____________∠=∠ 或AOB AOC ∠=∠____或AOB BOC ∠=∠____ 或AOC AOB ∠=∠____或BOC AOB ∠=∠____2、 如上图，_________2=∠AOB ，则OC 为AOB ∠的角平分线。

3、 如图，_____________________++=∠AOB ，_____________________________-=+=∠AOD4、 如图，从平角POQ ∠的顶点出发画一条射线OB ，OC OA 、分别是BOPQOB ∠∠、的角平分线，求AOC ∠的度数。

五、作业：如图，将书页斜折过去，使角的顶点A落在F处，BC为折痕，BD为EBF∠的度数。

∠的平分线，求CBD六、回顾反思我的收获：。

角
【学习目标】
1．认识并会表示角，知道角的常用度量单位，会进行简单的换算。

2．会比较、估计角的大小。

【学习重难点】
1．角的表示方法。

2．根据图形写出有关角的和与差的关系式。

【学习过程】
一、新知学习
1．你知道哪些角的表示方法？
2．角与角之间的大小是怎么比较的呢？
3．角的概念是什么？
4．角它是怎么度量的呢？
5．请写出度、分、秒的换算。

二、达标检测
1．下列语句正确的是（）。

A．有两条射线组成的图形叫做角
B．角的大小与角的两边长短无关
C．角的两边是射线，所以角不可度量
2．把周角平均分成60份，平均每份是_____。

3．1度=_____分；1分=_____秒。

4．129'
︒=_____″
5．2347
'''
︒=_____″。

角（2）学习目标1．在用量角器和直尺画一个角等于已知角的基础上，能够用圆规和直尺画一个角等于已知角；2．了解角平分线，并能够画出一个角的平分线；3．能够运用角平分线的知识，求简单的角的度数.学习难点用圆规和直尺画一个角等于已知角教学进程一、情景导入二、数学活动1.三角板画角2.量角器画角3.尺规画角（1）明确探讨关键.（2）“点”的确信.三．数学化熟悉1.尺规作图总结2.角平分线概念3.已知，如图OC 是∠AOB 的平分线，则∠AOC, ∠BOC, ∠AOB 这间有什么关系？四、例题讲解例⒈如图，若是∠AOD=80°，OC 是∠ AOD 内的一条射线，OB 是∠AO C 的平分线，∠AOB=30°.求∠AOC 与∠COD 的度数.五.基础训练1.与角的平分线类似，还有角的三等分线等，如图，①是OB 、OC 是∠A OD 的三等分线 ，②是一块扇形的材料，其中∠AOB=69°.你能过点O 画两条射线，将这块材料分成相同的3块吗？① ②2.你能画出红球在第一次反弹后的运动线路吗？3.如图，_____________________++=∠AOB ，_____________________________-=+=∠AODO A B D CB A O4.利用一副三角板上已知度数的角,不能画出的角是（ ）° ° ° °5.如图,∠COD 为平角,AO⊥OE,∠AOC = 2∠DOE,那么有∠AOC =____________｡6.如图，直线a 、b 的夹角为90°,∠1=50°,那么∠2=____________｡E AD O C。

课题§6.2角课型新授教学目标1．用直尺和圆规画一个角等于已知角．2．利用三角尺画一些特殊角．3．角平分线的定义及表示方法．4．进行简单的角的和、差、倍、分的计算．教学重点1、作一角等于已知角2、角平分线及角的和、差、倍分教学难点角平分线的认识、简单图形中角的计算教具准备投影仪教学过程教学内容教师活动内容、方式学生活动方式设计意图一、情境引入1、请叙述角的描述性定义2、角有哪几种表示方法？3、角的单位有几种，它们之间是如何换算的？4、动动手：用纸片剪一个角，将角对折，折痕将角分成两个相等的角。

角平分线的定义。

如图，OC将∠AOB分成相等的两部分，OC就是∠AOB的角平分线。

如果OC是∠AOB的角平分线，那么，∠AO C、∠BO C、∠AOB之间有怎样的关系呢？（学生归纳，教师总结）。

二、应用举例动动手：用一付三角板，可以拼出多少种不同的角？你能用手中的三角板画出300、60°角的平分线吗？解答：150、300、450、60°、750、900、1050、1200、1350、1500、1650、1800学生动手操作得出角平分线的定义，进而让学生总结它们的数量关系。

培养学生的动手、知识的运用能力CBAO【例题解析】例1、已知∠AOD=800，OB是∠AOC的平分线，∠AOB=300。

试求∠AOC、∠COD的度数。

（课本例题）可将题目先不给出要求的角而设置下面几个小问题：⑴在已知条件下你能求出那些角，说说你的理由；⑵如果你是老师你将会出一些什么样的求解问题？⑶如果已知∠AOD=800，OB是∠AOC的平分线，OC平分∠BOD你能求∠AOB的度数？（第（3）小题是将一个角三等分，问题：给你一个角，你能用手中的画图工具将这个三等分吗？如能说说你操作步骤）例2、作一个角等于已知角。

画法一：(用量角器)画法二：用直尺与圆规例3、已知∠AOB是直角，在外部的∠BOC=300。

OM平分∠AOB，ON平分∠BOC，求∠MON的度数。