黑龙江科技大学2.1.材料力学题库：轴向拉压内力答案

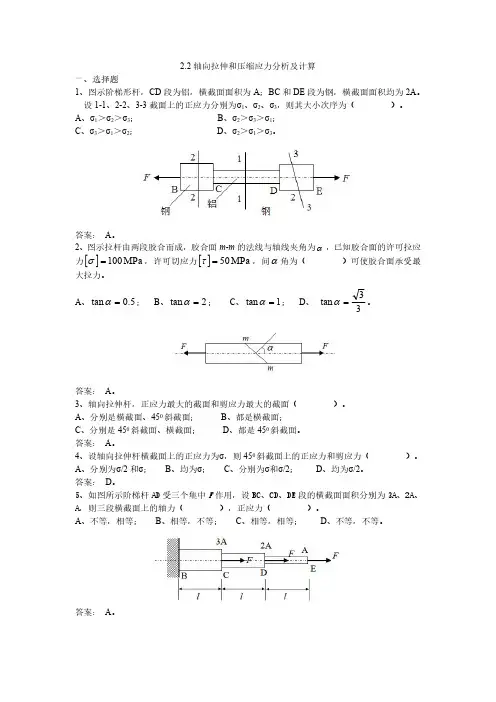
2.2轴向拉伸和压缩应力分析及计算一、选择题1、图示阶梯形杆，CD 段为铝，横截面面积为A ；BC 和DE 段为钢，横截面面积均为2A 。

设1-1、2-2、3-3截面上的正应力分别为σ1、σ2、σ3，则其大小次序为（）。

A 、σ1＞σ2＞σ3；B 、σ2＞σ3＞σ1；C 、σ3＞σ1＞σ2；D 、σ2＞σ1＞σ3。

答案：A 。

2、图示拉杆由两段胶合而成，胶合面m -m 的法线与轴线夹角为α，已知胶合面的许可拉应力[]100MPa σ=，许可切应力[]50MPa τ=，问α角为（）可使胶合面承受最大拉力。

A 、5.0tan =α；B 、2tan =α；C 、1tan =α；D 、33tan =α。

答案：A 。

3、轴向拉伸杆，正应力最大的截面和剪应力最大的截面（）。

A 、分别是横截面、450斜截面；B 、都是横截面；C 、分别是450斜截面、横截面；D 、都是450斜截面。

答案：A 。

4、设轴向拉伸杆横截面上的正应力为σ，则450斜截面上的正应力和剪应力（）。

A 、分别为σ/2和σ；B 、均为σ；C 、分别为σ和σ/2；D 、均为σ/2。

答案：D 。

5、如图所示阶梯杆AD 受三个集中F 作用，设BC、CD、DE 段的横截面面积分别为3A、2A、A，则三段横截面上的轴力（），正应力（）。

A 、不等，相等；B 、相等，不等；C 、相等，相等；D 、不等，不等。

答案：A 。

6、在A和B两点连接绳索ACB，绳索承受力为P，如图所示。

点A和B的距离保持不变，绳索的许用应力为[σ]。

当α角取（）度时，绳索用料最省。

A、0；B、30；C、45；D、60。

答案：C。

7、等直杆受力如图，横截面面积为100mm2，横截面m-m上的正应力为（）MPa。

A、50（拉应力）；B、40（压应力）；C、90（压应力）；D、90（拉应力）。

答案：D。

8、边长分别为100mm和50mm正方形截面杆，其两端作用相同的轴向载荷，两杆横截面上的正应力比为（）。

第2章 轴向拉伸和压缩主要知识点：（1）轴向拉伸（压缩）时杆的内力和应力；（2）轴向拉伸（压缩）时杆的变形；（3）材料在轴向拉伸和压缩时的力学性能；（4）轴向拉压杆的强度计算；（5）简单拉压超静定问题。

轴向拉伸（压缩）时杆的变形4. 一钢制阶梯杆如图所示。

已知沿轴线方向外力F 1=50kN ，F 2=20kN ，各段杆长l 1=100mm ，l 2=l 3=80mm ，横截面面积A 1=A 2=400mm 2，A 3=250mm 2，钢的弹性模量E=200GP a ，试求各段杆的纵向变形、杆的总变形量及各段杆的线应变。

解：（1）首先作出轴力图如图4-11所示，由图知kN F N 301-=，kN F F N N 2032==。

（2）计算各段杆的纵向变形m m EA l F l N 5693311111075.31040010200101001030---⨯-=⨯⨯⨯⨯⨯⨯-==∆ m m EA l F l N 569332222100.2104001020010801020---⨯=⨯⨯⨯⨯⨯⨯==∆(3)杆的总变形量m l l l l 53211045.1-⨯=∆+∆+∆=∆。

(4)计算各段杆的线应变 451111075.310.01075.3--⨯-=⨯-=∆=l l ε 45222105.208.0100.2--⨯=⨯=∆=l l ε 45333100.408.0102.3--⨯=⨯=∆=l l ε材料在轴向拉伸和压缩时的力学性能5. 试述低碳钢拉伸试验中的四个阶段，其应力—应变图上四个特征点的物理意义是什么？答：低碳钢拉伸试验中的四个阶段为弹性阶段、屈服阶段、强化阶段和颈缩阶段。

在弹性阶段，当应力小于比例极限σp 时，材料服从虎克定律；当应力小于弹性极限σe 时，材料的变形仍是弹性变形。

屈服阶段的最低点对应的应力称为屈服极限，以σs 表示。

强化阶段最高点所对应的应力称为材料的强度极限，以σb 表示，它是材料所能承受的最大应力。

轴向拉伸与压缩习题及解答Prepared on 22 November 2020轴向拉伸与压缩习题及解答一、判断改错1、构件内力的大小不但与外力大小有关，还与材料的截面形状有关。

答：错。

静定构件内力的大小之与外力的大小有关，与材料的截面无关。

2、杆件的某横截面上，若各点的正应力均为零，则该截面上的轴力为零。

答：对。

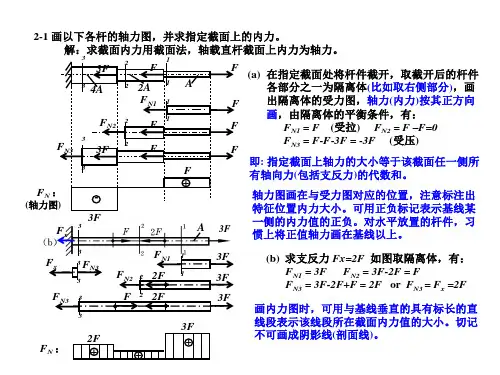
3、两根材料、长度都相同的等直柱子，一根的横截面积为1A ，另一根为2A ，且21A A >。

如图所示。

两杆都受自重作用。

则两杆最大压应力相等，最大压缩量也相等。

答：对。

自重作用时，最大压应力在两杆底端，即max max N All A Aνσν=== 也就是说，最大应力与面积无关，只与杆长有关。

所以两者的最大压应力相等。

最大压缩量为 2max max22N Al l l l A EA Eνν⋅∆===即最大压缩量与面积无关，只与杆长有关。

所以两杆的最大压缩量也相等。

A 1(a) (b)4、受集中力轴向拉伸的等直杆，在变形中任意两个横截面一定保持平行。

所以宗乡纤维的伸长量都相等，从而在横截面上的内力是均匀分布的。

答：错 。

在变形中，离开荷载作用处较远的两个横截面才保持平行，在荷载作用处，横截面不再保持平面，纵向纤维伸长不相等，应力分布复杂，不是均匀分布的。

5、若受力物体内某电测得x 和y 方向都有线应变x ε和y ε，则x 和y 方向肯定有正应力x σ和y σ。

答：错， 不一定。

由于横向效应作用，轴在x 方向受拉（压），则有x σ；y 方向不受力，但横向效应使y 方向产生线应变，y x εενε'==-。

二、填空题1、轴向拉伸的等直杆，杆内的任一点处最大剪应力的方向与轴线成（45）2、受轴向拉伸的等直杆，在变形后其体积将（增大）3、低碳钢经过冷做硬化处理后，它的（比例）极限得到了明显的提高。

4、工程上通常把延伸率δ>（5%）的材料成为塑性材料。

5、 一空心圆截面直杆，其内、外径之比为，两端承受力力作用，如将内外径增加一倍，则其抗拉刚度将是原来的（4）倍。

2.3轴向拉伸和压缩变形分析及计算一、选择题1、图示平板，两端受均布载荷q 作用，若变形前在板面上画两条平行线段AB 和CD ，则变形后（）。

A 、AB//CD ，α角减小；B 、AB//CD ，α角不变；C 、AB//CD ，α角增大；D 、AB 不平行于CD 。

答案：A 。

2、甲乙两杆，几何尺寸相同，轴向拉力相同，材料不同，它们的应力和变形有四种可能，下列（）是正确的。

A 、应力σ和变形l ∆相同；B 、应力σ不同和变形l ∆相同；C 、应力σ相同和变形l ∆不同；D 、应力σ不同和变形l ∆不同。

答案：C 。

3、图示结构中，杆①的材料是钢，GPa E 2061=；杆②的材料是铝，GPa E 702=；已知两杆的横截面积相等，则在力F 作用下，节点A （）。

A 、向左下方移动；B 、向右下方移动；C 、沿铅垂方向向下移动；D、不动。

答案：A 。

4、图示拉杆的外表面上有一斜线，当拉杆变形时，斜线将（）。

A 、平动；B 、转动；C 、不动；D 、平动加转动。

答案：D 。

5、有同一种材料组成的变截面杆的横截面面积分别为A2和A，受力如图所示，弹性模量E 为常数；以下结论（）是正确的。

A、D截面位移为2FlEA；B、D截面位移为2FlEA；C、C截面位移为2FlEA；D、C截面位移为2FlEA。

答案：A。

6、刚性杆AB由三根材料、横截面面积均相同的杆吊杆。

在结构中（）为零。

A、杆①的轴力；B、杆②的轴力；C、A点的水平位移；D、A点的垂直位移。

答案：B。

7、一圆杆受轴向拉力，在其弹性变形范围内，将直径增加一倍其他条件不变，则杆的相对变形与原变形的比值为（）。

A、1/4；B、1/2；C、1；D、4。

答案：A。

8、长度和横截面面积均相同的两杆，一为钢杆，另一为铝杆，在相同的轴向拉力作用下，下列关于两杆的应力与变形的描述，正确的是（）。

A、铝杆的应力和钢杆相同，变形大于钢杆；B、铝杆的应力和钢杆相同，变形小于钢杆；C、铝杆的应力和变形均大于钢杆；D、铝杆的应力和变形均小于钢杆。

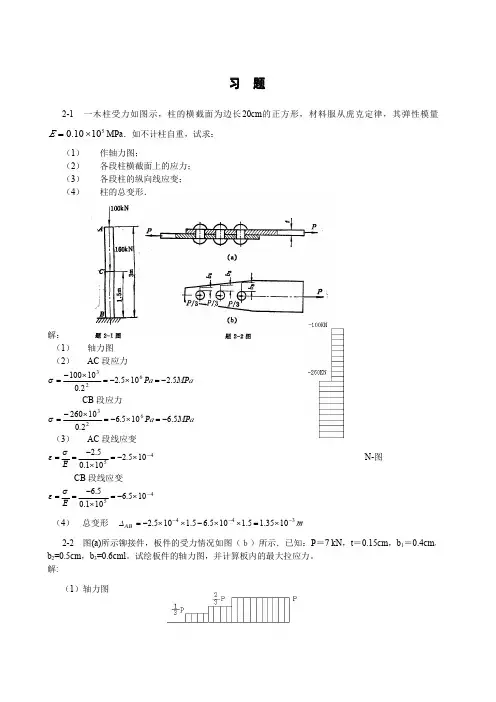
第二章轴向拉伸与压缩2- 1 试求图示直杆横截面1- 1、2- 2、3- 3上的轴力，并画出轴力图。

2- 2 图示中部对称开槽直杆，试求横截面1-1 和 2-2上的正应力。

12F.F=14kN..(a)1F1FFFF2F323F N1F N2F N32+F=2kNFF N1= - 2kN1220102044解：1．轴力F N (kN)F1=18kN (b)18kN18kNF N (kN)21 F 2=3kN2F3=25kN12F N1F N33kNF N21815F N2 = 0kNF N3= 2kN3F4=10kN310kN10+F N1= - 18kNF N2= - 15kNF N3= 10kN由截面法可求得，杆各横截面上的轴力为F N F14kN2．应力103F N14175MPa1 1A1 120MPa4F N14 103350 MPa2 2A220MPa210 42- 3 图示桅杆起重机， 起重杆 AB 的横截面是外径为 20 mm 、内径为 18 mm 的圆环， 钢丝绳 BC 的横截面面积为 10 mm 2。

试求起重杆AB 和钢丝绳 BC 横截面上的应力。

yBF N BCB. 45C30o15oxFFN AB. 15F=2kNA.解：1．轴力取节点 B 为研究对象，受力如图所示，F x 0 ： F NBC F NAB cos30 F cos 45F y0 ：F N AB sin 30F sin 45由此解得： FNAB2.83 kN ，FNBC1.04 kN2．应力起重杆横截面上的应力为ABFNAB2.83 103MPa47.4 MPaA AB2 220 184钢丝绳横截面上的应力为BC F N BC1.04 103MPa 104 MPaABC102- 4 图示由铜和钢两种材料组成的等直杆，铜和钢的弹性模量分别为E1100 GPa 和 E2210 GPa 。

若 杆 的 总 伸 长 为l 0.126 mm ，试求载荷 F 和杆横截面上的应力。

材料⼒学答案第⼆章轴向拉压应⼒与材料的⼒学性能2-1试画图⽰各杆的轴⼒图。

题2-1图解：各杆的轴⼒图如图2-1所⽰。

图2-12-2试画图⽰各杆的轴⼒图，并指出轴⼒的最⼤值。

图a与b所⽰分布载荷均沿杆轴均匀分布，集度为q。

题2-2图(a)解：由图2-2a(1)可知，轴⼒图如图2-2a(2)所⽰，图2-2a(b)解：由图2-2b(2)可知，轴⼒图如图2-2b(2)所⽰，图2-2b2-3图⽰轴向受拉等截⾯杆，横截⾯⾯积A=500mm2，载荷F=50kN。

试求图⽰斜截⾯m-m上的正应⼒与切应⼒，以及杆内的最⼤正应⼒与最⼤切应⼒。

题2-3图解：该拉杆横截⾯上的正应⼒为斜截⾯m-m的⽅位⾓，ο=α故有-50杆内的最⼤正应⼒与最⼤切应⼒分别为2-5某材料的应⼒-应变曲线如图所⽰，图中还同时画出了低应变区的详图。

试确定材料的弹性模量E、⽐例极限σ、屈服极限sσ、强度极限bσ与伸长率δ，p并判断该材料属于何种类型（塑性或脆性材料）。

题2-5解：由题图可以近似确定所求各量。

MPa 220p ≈σ, MPa 240s ≈σMPa 440b ≈σ, %7.29≈δ该材料属于塑性材料。

2-7 ⼀圆截⾯杆，材料的应⼒-应变曲线如题2-6图所⽰。

若杆径d =10mm ，杆长 l =200mm ，杆端承受轴向拉⼒F = 20kN 作⽤，试计算拉⼒作⽤时与卸去后杆的轴向变形。

题2-6图解：255MPa Pa 1055.2m0.010πN 102048223=?===A F σ查上述εσ-曲线，知此时的轴向应变为轴向变形为拉⼒卸去后，有00364.0e =ε， 00026.0p =ε故残留轴向变形为2-9 图⽰含圆孔板件，承受轴向载荷F 作⽤。

已知载荷F =32kN ，板宽b=100mm ，板厚=δ15mm ，孔径d =20mm 。

试求板件横截⾯上的最⼤拉应⼒（考虑应⼒集中）。

题2-9图解：根据查应⼒集中因数曲线,得根据δd b Fσ)(n -=， n max σσK =得2-10 图⽰板件，承受轴向载荷F 作⽤。

3、材料拉压力学性能一、选择题1、作为脆性材料的极限应力是（）。

A 、比例极限；B 、弹性极限；C 、屈服极限；D 、强度极限。

答案：B 。

2、材料的塑性指标有（）。

A 、σS 和δ；B 、σS 和ψ；C 、δ和ψ；D 、σS 、δ和ψ。

答案：C 。

3、用三种不同材料制成尺寸相同的试件，在相同的试验条件下进行拉伸实验，得到应力－应变曲线图。

比较三条曲线，可知拉伸强度最高、弹性模量最大、塑性最好的材料分别是（）。

A 、a 、b 、c ；B 、b 、c 、a ；C 、b 、a 、c ；D 、c 、b 、a 。

答案：A 。

4、一拉伸钢杆，弹性模量E ＝200GPa ，比例极限为200MPa ，今测得其轴向应变ε＝0.0015，则横截面上的正应力（）。

A 、σ＝Eε＝300MPa ；B 、σ＞300MPa ；C 、200MPa ＜σ＜300MPa ；D 、σ＜200MPa 。

答案：C 。

5、低碳钢拉伸经过冷作硬化后，以下四种指标中（）将得到提高。

A 、强度极限；B 、比例极限；C 、断面收缩率；D 、延伸率。

答案：C 。

6、当低碳钢试件的拉伸试验应力s σσ=时，试件将（）。

A 、完全失去承载能力；B 、断裂；C 、发生局部颈缩现象；D 、产生很大的塑性变形。

答案：D 。

7、对于拉伸曲线上没有明显屈服极限平台的一般塑性材料，工程上规定2.0σ作为名义屈服应力，此时对应的（）。

A 、应变量为0.2%ε=；B 、塑性应变量为0.2%ε=；C 、应变量为0.2ε=；D 、塑性应变量为0.2ε=。

答案：A 。

8、所有脆性材料，它与塑性材料相比，其拉伸力学性能的最大特点是（）。

A、强度低，对应力集中不敏感；B、相同拉力作用下变形小；C、断裂前几乎没有塑性变形；D、应力-应变关系严格遵循胡克定律。

答案：C。

9、现有钢、铸铁两种杆材，其直径相同。

从承载能力与经济效益两个方面考虑，如图示结构中两种合理选择方案是（）。

A、1杆为钢，2杆为铸铁；B、1杆为铸铁，2杆为钢；C、1、2杆均为钢；D、1、2杆均为铸铁。

材料力学轴向拉压题目+答案详解-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN2-4. 图示结构中，1、2两杆的横截面直径分别为10mm 和20mm ，试求两杆内的应力。

设两根横梁皆为刚体。

解：（1）以整体为研究对象，易见A 处的水平约束反力为零；（2）以AB 为研究对象由平衡方程知0===A B B R Y X（3）以杆BD 为研究对象由平衡方程求得1KNN N NY KNN N mC20010 01001101 021211==--===⨯-⨯=∑∑（4）杆内的应力为MPa A N MPa A N 7.63204102012710410102322223111=⨯⨯⨯===⨯⨯⨯==πσπσ2-19. 在图示结构中，设AB 和CD 为刚杆，重量不计。

铝杆EF 的l 1=1m ，A 1=500mm 2，E 1=70GPa 。

钢杆AC 的l 2=1.5m ，A 2=300mm 2，E 2=200GPa 。

若载荷作用点G 的垂直位移不得超过2.5mm 。

试求P 的数值。

解：（1）由平衡条件求出EF 和AC 杆的内力P N N N P N N AC EF AC 4332 2112=====（2）求G 处的位移22221111212243)ΔΔ23(21)ΔΔ(21Δ21ΔA E l N A E l N l l l l l l A C G +=+=+==（3）由题意kNP P P A E Pl A E Pl mml G 1125.2300102001500500107010009212143435.233222111≤∴≤⨯⨯⨯+⨯⨯⨯⨯=⨯⨯+⨯⨯≤ 2-27. 在图示简单杆系中，设AB 和AC 分别是直径 为20mm 和24mm 的圆截面杆，E=200GPa ，P=5kN ，试求A 点的垂直位移。

解：（1）以铰A 为研究对象，计算杆AB 和杆AC 的受力kN N kN N AC AB 66.3 48.4==（2）两杆的变形为()伸长mm πEA l N l ABAB AB AB 201.04201020045cos 20001048.42303=⨯⨯⨯⨯⨯==Δ ()缩短mm πEA l N l ACAC AC AC 0934.04241020030cos 20001066.32303=⨯⨯⨯⨯⨯==Δ（3）如图，A 点受力后将位移至A ’,所以A 点的垂直位移为AA ’’mmctg A A l A A AA A A mmA A ctg A A ctg A A A mm AA AA AA AA A A A A l l AB A AB AC 249.00355.0284.0 4545sin /Δ 035.0 4530A 0972.030sin /45sin /AΔΔAA ΔAA 00330043010243434321=-='''-=''-=''=∴='''∴'''+'''==-=-='==δ 又中在图中2-36. 在图示结构中，设AC 梁为刚杆，杆件1、2、3的横截面面积相等，材料相同。

第二章 轴向拉伸和压缩2-1 一圆截面直杆，其直径d ＝20mm, 长L =40m ，材料的弹性模量E =200GPa ，容重γ＝80kN/m 3, 杆的上端固定，下端作用有拉力F =4KN ，试求此杆的：⑴最大正应力； ⑵最大线应变； ⑶最大切应力；⑷下端处横截面的位移∆。

题 2 - 1 图+5004.8N4000N解：首先作直杆的轴力图⑴最大的轴向拉力为232N,max 80100.024*********.8N 44d F V F L F ππγγ=+=+=⨯⨯⨯⨯+=故最大正应力为：N,maxN,maxN,maxmax 222445004.8=15.94MPa 3.140.024F F F Addσππ⨯====⨯⑵最大线应变为:64maxmax915.94100.7971020010E σε-⨯===⨯⨯ ⑶当α（α为杆内斜截面与横截面的夹角）为45︒时，maxmax 7.97MPa 2ασττ===⑷取A 点为x 轴起点，2N (25.124000)N 4d F Vx F x F x πγγ=+=+=+故下端处横截面的位移为：240N 0025.1240001d d (12.564000)2.87mm LL F x x x x x EA EA EA+∆===⋅+=⎰⎰2-2 试求垂直悬挂且仅受自重作用的等截面直杆的总伸长△L 。

已知杆横截面面积为A ，长度为L ,材料的容重为γ。

AB题 2-2 图A B解：距离A 为x 处的轴力为N ()F x Ax γ=⋅ 所以总伸长 2N 00()L d d 2LL F x Ax L x x EA EA Eγγ∆===⎰⎰ 2-3 图示结构，已知两杆的横截面面积均为A =200mm 2,材料的弹性模量E =200GPa 。

在结点A 处受荷载F 作用，今通过试验测得两杆的纵向线应变分别为ε1＝4×10－4，ε2＝2×10－4，试确定荷载P 及其方位角θ的大小。

轴向拉伸与压缩习题及解答(总31页)-本页仅作为预览文档封面，使用时请删除本页-轴向拉伸与压缩习题及解答计算题1：利用截面法，求图2. 1所示简支梁m — m 面的内力分量。

解：（1）将外力F 分解为两个分量，垂直于梁轴线的分量F sin θ,沿梁轴线的分量F cos θ.(2)求支座A 的约束反力：xF∑=0，Ax F ∑=cos F θB M ∑=0, Ay F L=sin 3L F θAy F =sin 3Fθ (3)切开m — m ，抛去右半部分，右半部分对左半部分的作用力N F ，S F 合力偶M 代替 （图 ）。

图 图(a)以左半段为研究对象，由平衡条件可以得到xF∑=0， N F =—Ax F =—cos F θ（负号表示与假设方向相反）y F ∑=0， s F =Ay F =sin 3Fθ 左半段所有力对截面m-m 德形心C 的合力距为零sin θC M ∑=0， M=AyF 2L =6FLsin θ 讨论 对平面问题，杆件截面上的内力分量只有三个：和截面外法线重合的内力称为轴力，矢量与外法线垂直的力偶距称为弯矩。

这些内力分量根据截面法很容易求得。

在材料力学课程中主要讨论平面问题。

计算题2：试求题2-2图所示的各杆1-1和2-2横截面上的轴力，并作轴力图。

解 （a ）如图（a ）所示，解除约束，代之以约束反力，作受力图，如题2-2图（1a ）所示。

利用静力学平衡条件，确定约束反力的大小和方向，并标示在题2-2图（1a ）中。

作杆左端面的外法线n ，将受力图中各力标以正负号，凡与外法线指向一致的力标以正号，反之标以负号，轴力图是平行于杆轴线的直线。

轴力图在有轴力作用处，要发生突变，突变量等与该处轴力的数值，对于正的外力，轴力图向上突变，对于负的外力，轴力图向下突变，如题2-2图（2a ）所示，截面1和截面2上的轴力分别为1N F =F 和2N F =—F 。

(b)解题步骤与题2-2（a ）相同，杆受力图和轴力图如题2-2（1b ）、（2b ）所示。