下载文档原格式
execl函数经纬度计算距离
Excel函数可以方便地计算两个经纬度之间的距离。
这个功能可以在很多领域得到应用，比如航空、航海、城市规划等等。
使用Excel函数计算经纬度距离的方法如下：1. 在Excel 中打开一个新的工作表。
2. 在第一行输入两个经度和两个纬度的值，分别表示起点和终点的经纬度。
3. 在第二行输入以下公式：=ACOS(COS(RADIANS(90-起点纬度))*COS(RADIANS(90-终点纬度))+SIN(RADIANS(90-起点纬度))*SIN(RADIANS(90-终点纬度))*COS(RADIANS(起点经度-终点经度)))*6371.004
4. 按下回车键，Excel会自动计算出两个经纬度之间的距离，单位为公里。
需要注意的是，这个公式只适用于计算地球表面上两点之间的直线距离，不考虑地球的曲率和海拔高度等因素。
但是在大多数情况下，这个公式已经足够准确了。
使用Excel函数计算经纬度距离是一种简单而实用的方法，可以帮助我们在各种领域中更好地规划和安排。
通过经纬度坐标计算距离的方法宝子们，今天咱们来唠唠通过经纬度坐标计算距离这个超酷的事儿。
咱先得知道，地球呢是个近似球体的家伙。
经纬度就像是地球这个大球上的坐标网。
纬度呢，是用来表示南北方向的位置，赤道就是0°纬线，越往两极，纬度数值越大。
经度呢，是表示东西方向的位置，本初子午线是0°经线。
那怎么根据经纬度来算距离呢？这里面有个简单又有趣的小公式哦。
不过这个公式对于咱们日常聊天来说有点小复杂，但咱可以简单理解下原理。
在赤道附近，经度每相差1°，距离大概相差111千米，因为赤道周长大概是4万千米，360°一平分，就差不多是这个数啦。
但越往两极呢，这个经度之间的距离就会变小，因为纬线的长度在变小呀。
对于纬度来说，每相差1°，距离大概也是111千米。
不管是在北半球还是南半球，这个规律都差不多。
比如说，有个地方A是北纬30°，东经120°，另一个地方B是北纬31°，东经120°，那这两个地方大概就在同一条经线上，它们的距离就大概是111千米。
要是两个地方的经纬度都不一样呢？那就稍微复杂点啦。
不过咱不用太纠结那些超级复杂的数学计算。
现在有好多手机软件或者在线工具，只要输入经纬度，就能轻松算出距离。
宝子们，这经纬度算距离可不仅仅是个数学题哦。
它在好多地方都特别有用。
比如说航海的时候，船员们要知道自己离目的地还有多远，就可以根据经纬度来算。
还有那些喜欢野外探险的小伙伴，要是知道了自己的经纬度和营地的经纬度，就能大概算出距离，心里也能有个底。
咱就把这个经纬度算距离当成一个超有趣的小秘密。
下次跟朋友聊天的时候，就可以拿出来显摆一下。
比如说，你可以说“宝子，你知道不，根据经纬度能算出两个地方的距离呢，可神奇啦。
”然后再简单讲讲原理，保证你的朋友们都会对你刮目相看的呢。
这小小的经纬度里可是藏着大大的学问，就像生活中的小惊喜一样，等着咱们去发现。
经纬度定位计算距离在现代科技的帮助下，我们可以轻松获取到地球上任意两点之间的经纬度坐标。
然而，仅有经纬度坐标是无法直观地知道这两点之间的距离的。
因此，我们需要借助数学和计算机编程的力量来计算经纬度定位之间的距离。
在计算经纬度定位之间的距离之前，我们需要先了解一些背景知识。
经度和纬度是地球表面上的两个基本地理坐标系统。
经度用来表示地球上的东西方向，从-180度到180度。
纬度则用来表示地球上的南北方向，从-90度到90度。
当我们获得了两个点的经纬度坐标后，如何计算它们之间的距离呢？有许多算法可以用来计算经纬度定位之间的距离，其中最常用的是Haversine公式。
Haversine公式基于球面三角学来计算地球上任意两点之间的最短距离。
这个公式的原理是将球面上的两点与球心连线看作是一个圆锥台，然后计算两个圆锥台的体积之差，最后得到的结果即为两点之间的距离。
下面是一个用Python编程语言实现Haversine公式的例子：```python import mathdef calculate_distance(lat1, lon1, lat2, lon2): R = 6371 # 地球半径，单位为千米lat1_rad = math.radians(lat1)lon1_rad = math.radians(lon1)lat2_rad = math.radians(lat2)lon2_rad = math.radians(lon2)delta_lon = lon2_rad - lon1_raddelta_lat = lat2_rad - lat1_rada = math.sin(delta_lat/2)**2 + math.cos(lat1_rad) * math.cos(lat2_rad)* math.sin(delta_lon/2)**2c = 2 * math.atan2(math.sqrt(a), math.sqrt(1-a))distance = R * creturn distance示例坐标点lat1 = 39.9042 lon1 = 116.4074 lat2 = 31.2304 lon2 = 121.4737distance = calculate_distance(lat1, lon1, lat2, lon2) print(。
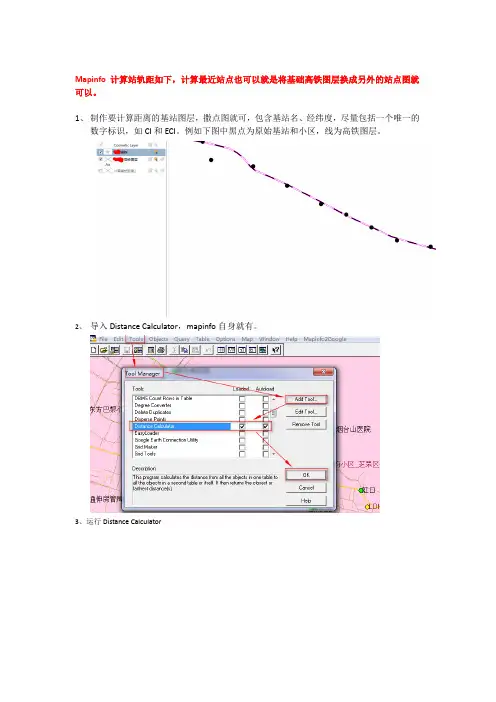
Mapinfo计算站轨距如下，计算最近站点也可以就是将基础高铁图层换成另外的站点图就可以。
1、制作要计算距离的基站图层，撒点图就可，包含基站名、经纬度，尽量包括一个唯一的
数字标识，如CI和ECI。
例如下图中黑点为原始基站和小区，线为高铁图层。
2、导入Distance Calculator，mapinfo自身就有。
3、运行Distance Calculator
4、根据界面进行选择（记得单位默认是miles英里，最好选择meters米），最后点Calculate Distance进行计算
5、保存计算的结果（tab格式文件）
6、MAPINFO打开保存的TAB文件
6、TABLE-EXPORT
然后选择对应的图层-export：
选择txt格式（或csv格式），保存：
7、最好打开保存的txt文件，里面包含有原始基站名、最近距离的目标基站名，以及两基站的距离。
注意！如果基站名太长（好像是23个字符，最好别超过20个），计算结果显示会出错：。
坐标算距离用什么软件在日常生活中，经常会遇到需要计算两个坐标之间距离的情况，例如寻找最近的餐馆、测量行车距离等。
为了解决这类问题，我们可以借助一些专门用于坐标距离计算的软件，以方便快捷地获取所需信息。
下面将介绍几种常见的软件工具，供大家参考选择。
1. Google 地图Google 地图是一款广泛使用的在线地图服务，除了提供详细的地图信息外，它还内置了坐标计算功能。
使用 Google 地图计算两个坐标之间的距离非常简单，只需要在地图上选择两个位置点，系统会自动显示它们之间的直线距离。
此外，Google 地图还可以提供基于路网的行车距离计算、交通状况估计等实用功能。
2. 百度地图百度地图是中国领先的在线地图服务平台，类似于 Google 地图，它也提供了坐标计算的功能。
用户可以在百度地图上标注两个位置点，系统会准确计算出它们之间的直线距离。
百度地图还有详细的公交、驾车、步行导航功能，能够给出基于实际路线的行车距离。
3. 高德地图高德地图是中国领先的综合导航、交通及地理位置大数据解决方案平台，除了提供地图和导航服务外，也具备坐标距离计算功能。
用户可以在高德地图上选择两个位置点，并通过使用内置的测量工具快速获取它们之间的直线距离。
高德地图还拥有优秀的路径规划和导航功能，可以帮助用户实现准确的行车距离计算。
4. GPS 测距（手机应用）除了利用在线地图服务外，还可以通过一些专门用于测量距离的手机应用来计算坐标之间的距离。
GPS 测距是其中一种常见的应用程序，可以通过手机的 GPS功能获取当前位置的经纬度，并测量距离。
用户可以手动输入坐标或使用地图界面选择位置点，并获取它们之间的直线距离。
GPS 测距还支持记录轨迹、计算面积等实用功能，方便用户做更多地理测量应用。
请注意：以上介绍的软件工具均是常见且免费的，用户可以根据自身需求和习惯选择合适的软件来计算坐标之间的距离。
值得一提的是，这些软件通常都需要联网才能正确使用定位功能，因此，在使用过程中，请确保网络连接畅通。
怎么用经纬度计算两地之间的距离经纬度是地球上一点的坐标表示方法，可以用来计算两个点之间的距离。
计算两地之间的距离可以使用多种方法，包括球面距离公式、大圆航线距离和Vincenty算法等。
下面将详细介绍这些方法。
1.球面距离公式球面距离公式是最简单且最常用的计算两点之间距离的方法。
它基于球面三角形的边长计算两点之间的距离，如下所示：d = R * arccos(sin(lat1) * sin(lat2) + cos(lat1) * cos(lat2) * cos(lon2 - lon1))其中，d是两点之间的球面距离，R是地球的平均半径，lat1和lat2是两点的纬度，lon1和lon2是两点的经度。
2.大圆航线距离大圆航线距离是计算两点之间最短距离的方法，它基于地球表面上连接两点的最短弧线，如下所示：d = R * arccos(sin(lat1) * sin(lat2) + cos(lat1) * cos(lat2) * cos(lon2 - lon1))其中，d是两点之间的大圆航线距离，R是地球的半径，lat1和lat2是两点的纬度，lon1和lon2是两点的经度。
3. Vincenty算法Vincenty算法是一种更精确的计算两点之间距离的方法，它基于椭球体模型而不是简单地球模型。
该算法能够考虑地球形状的扁平化，并且适用于短距离和长距离的计算。
具体实现需要迭代计算，公式略显繁琐，如下所示：a=R1,b=R2,f=(a-b)/aL = L2 - L1, U1 = atan((1 - f) * tan(lat1)), U2 = atan((1 - f) * tan(lat2))sinU1 = sin(U1), cosU1 = cos(U1), sinU2 = sin(U2), cosU2 = cos(U2)λ=L,λʹ=2πwhile (，λ - λʹ， > 10e-12):sinλ = sin(λ), cosλ = cos(λ), sinσ = sqrt((cosU2 *sinλ) * (cosU2 * sinλ) + (cosU1 * sinU2 - sinU1 * cosU2 *cosλ) * (cosU1 * sinU2 - sinU1 * cosU2 * cosλ))cosσ = sinU1 * sinU2 + cosU1 * cosU2 * cosλσ = atan2(sinσ, cosσ)sinα = cosU1 * cosU2 * sinλ / sinσcos²α = 1 - sinα * sinαcos2σm = cosσ - 2 * sinU1 * sinU2 / cos²αC = f / 16 * cos²α * (4 + f * (4 - 3 * cos²α))λʹ=λλ = L + (1 - C) * f * sinα * (σ + C * sinσ * (cos2σm + C * cosσ * (-1 + 2 * cos2σm * cos2σm)))u² = cos²α * (a*a - b*b) / (b*b)B=u²/1024*(256+u²*(-128+u²*(74-47*u²)))Δσ = B / 6 * (cosσ * (-1 + 2 * cos2σm * cos2σm) - B / 4 * (cos2σm * (-3 + 4 * sinσ * sinσ) - B / 6 * cosσ * (-3 + 4 * cos2σm * cos2σm) * (-3 + 4 * sinσ * sinσ)))s=b*A*(σ-Δσ)其中，a和b是地球的长半轴和短半轴，f是扁平度参数，R1和R2是两点的曲率半径，L1和L2是两点的经度差，lat1和lat2是两点的纬度。
根据经纬度算距离
经纬度距离计算简单方法：
1) 根据最长的纬线，即0度纬线，也就是赤道，计算经度的距离。
赤道周长：40075704m(约4万km），所以，1度经度最大距离等于40075704/360=111321m（约111km）。
0.0001度经度最大距离等于11.132m。
0.000001度经度最大距离是0.1113m。
2) 根据经线长度，计算纬度的距离。
子午线周长：40008548m(约4万km，所以，1度纬度最大距离等于40008548/360=111134m（约111km）。
0.0001度经度最大距离等于11.113m。
0.000001度经度最大距离等于0.1111m。
所以说，经纬度相差0.000001度时候，距离相差位0.111m。
这个精度已经满足了绝大部分GIS应用的需求，所以各大在线地图的坐标也都保留到了第6位。
结论：
相差1经度或者1纬度，球面距离约为111 千米
相差0.000001经度或者0.000001纬度，球面距离为0.11 米
1。
经纬测量距离操作方法经纬测量距离是一种基于球面几何原理的测量方法，用来确定地球上两点之间的直线距离。
这种方法的原理是利用经度和纬度的差异来计算两个点之间的距离。
首先，我们需要了解经度和纬度的概念。
经度是指以本初子午线为基准，沿着地球赤道周围的大圆线划分出来的线条，用来表示地球上一个点的东西方向位置。
纬度是指以地球自转轴为基准，沿着地球经度线圈划分出来的线条，用来表示地球上一个点的南北方向位置。
在经纬测量距离之前，需要明确两个点的经纬度坐标。
这可以通过地图或者GPS 定位系统来获取。
接下来，我们可以使用球面三角学公式来计算两个点之间的距离。
常用的方法包括大圆弧长公式和球面三角解算法。
下面我将对这两种方法分别进行介绍。
第一种方法是大圆弧长公式。
这个公式利用两点之间的经度和纬度差异以及地球的半径来计算两个点之间的最短距离。
这个公式的计算比较简单，可以使用以下公式进行计算：d = R * arccos(sin(φ1) * sin(φ2) + cos(φ1) * cos(φ2) * cos(Δλ))其中，d表示两点间距离，R表示地球的半径（一般取6371km），φ1和φ2分别为两点的纬度，Δλ为两点的经度差。
第二种方法是球面三角解算法。
这种方法通过计算两点间的球面三角形边长来确定距离。
这个方法的计算较为复杂，需要使用正弦定理和余弦定理等三角学原理。
具体的计算过程如下：1. 计算两点经纬度之差：Δφ= φ2 - φ1Δλ= λ2 - λ12. 将经纬度差转化为弧度：Δφ' = Δφ* π/ 180Δλ' = Δλ* π/ 1803. 计算两点间的球面角度距离：a = sin²(Δφ' / 2) + cos(φ1) * cos(φ2) * sin²(Δλ' / 2)4. 计算球面角度距离对应的弧长：c = 2 * atan2(√a, √(1-a))5. 将弧长转化为实际距离：d = R * c其中，d表示两点间距离，R表示地球的半径。
根据两点经纬度计算距离
明确了两点的经纬度，可以有多种方法计算这两点间的距离，下面将介绍两种方法：
一、Google地球中直接量算
这是最简单的方法。
打开Google地球，点击图钉标志，分别将两点坐标输入，你会在地图上看到你刚输入的两个点，这时你可以直接在工具栏中选择距离量算，起点是其中一个点，终点为另一个点，此时量算的结构就是两点间的距离。
二、变换直角坐标求距离
这个方法类似于在平面中求解，假设你的两点A1（e1，n1）、A2（e2，n2），可以利用坐标转换器将坐标首先转成直角坐标（注：任何一款GIS软件都可以实现坐标转换）得到A1（x1，y1）、A2（x2，y2），那么接下来的工作就比较简单了，利用高中时学过的两点间距离公式：
A1A2=x1−x22+y1−y22。
java 经纬度点到线段的最短距离在地理信息系统中，经纬度是一种常见的坐标表示方式。
在实际应用中，我们经常需要计算一个点到一条线段的最短距离。
这个问题在很多领域都有应用，比如地图导航、航空航海、城市规划等等。
本文将介绍如何使用Java语言计算经纬度点到线段的最短距离。
我们需要了解一些基本概念。
在地理信息系统中，经纬度是用来表示地球上某个点的坐标的。
经度表示东西方向，纬度表示南北方向。
经度的取值范围是-180到180度，纬度的取值范围是-90到90度。
一条线段可以用两个点来表示，每个点都有经度和纬度两个坐标。
计算一个点到一条线段的最短距离，可以分为以下几个步骤：1. 将经纬度转换为直角坐标系中的点。
这个可以使用球面坐标系转换公式来实现。
2. 将线段的两个点也转换为直角坐标系中的点。
3. 计算点到线段的垂线的交点。
这个可以使用向量的投影来实现。
4. 计算点到交点的距离，即为点到线段的最短距离。
下面是Java代码实现：```javapublic class PointToLineDistance {public static void main(String[] args) {// 点的经纬度坐标double lat1 = 39.9087;double lng1 = 116.3975;// 线段的两个点的经纬度坐标double lat2 = 39.9037;double lng2 = 116.3915;double lat3 = 39.9137;double lng3 = 116.4015;// 将经纬度转换为直角坐标系中的点double[] p1 = latLngToXYZ(lat1, lng1);double[] p2 = latLngToXYZ(lat2, lng2);double[] p3 = latLngToXYZ(lat3, lng3);// 计算点到线段的垂线的交点double[] p = projectPointOnLine(p1, p2, p3);// 计算点到交点的距离double distance = distance(p1, p);System.out.println("点到线段的最短距离为：" + distance); }// 经纬度转换为直角坐标系中的点public static double[] latLngToXYZ(double lat, double lng) {double[] xyz = new double[3];double r = 6371; // 地球半径xyz[0] = r * Math.cos(Math.toRadians(lat)) * Math.cos(Math.toRadians(lng));xyz[1] = r * Math.cos(Math.toRadians(lat)) * Math.sin(Math.toRadians(lng));xyz[2] = r * Math.sin(Math.toRadians(lat));return xyz;}// 计算点到线段的垂线的交点public static double[] projectPointOnLine(double[] p1, double[] p2, double[] p3) {double[] v1 = new double[3];double[] v2 = new double[3];for (int i = 0; i < 3; i++) {v1[i] = p3[i] - p1[i];v2[i] = p2[i] - p1[i];}double dot = dotProduct(v1, v2);double len2 = dotProduct(v2, v2);double[] p = new double[3];for (int i = 0; i < 3; i++) {p[i] = p1[i] + dot / len2 * v2[i];}return p;}// 计算两个向量的点积public static double dotProduct(double[] v1, double[] v2) { double dot = 0;for (int i = 0; i < 3; i++) {dot += v1[i] * v2[i];}return dot;}// 计算两个点之间的距离public static double distance(double[] p1, double[] p2) { double dx = p1[0] - p2[0];double dy = p1[1] - p2[1];double dz = p1[2] - p2[2];return Math.sqrt(dx * dx + dy * dy + dz * dz);}}```在上面的代码中，我们首先定义了一个`latLngToXYZ`方法，用来将经纬度转换为直角坐标系中的点。
java 经纬度点到线段的最短距离
在Java中，如何计算一个经纬度点到一条线段的最短距离呢？这是一个很常见的问题，在地理信息系统和地图应用中经常会遇到。
首先，需要将经纬度转换为平面坐标系，可以使用投影算法（如墨卡托投影、等角圆柱投影等）。
然后，可以使用向量运算来计算点到线段的垂线的长度，从而得到最短距离。
具体来说，可以将线段的两个端点分别表示为向量 a 和 b，将点表示为向量 p。
然后，计算向量 ap 和向量 ab 的夹角θ，如果θ大于 90 度，则点 p 到线段 ab 的最短距离为点 p 到线段端点 a 的距离；如果θ小于 90 度，则点 p 到线段 ab 的最短距离为向量 ap 在向量 ab 方向上的投影长度。
在 Java 中，可以使用 Math 库中的数学函数来计算向量的模、点积、距离等。
需要注意的是，在计算距离时，需要将平面坐标系中的距离转换为地球表面的距离，可以使用 Haversine 公式等方法来进行转换。
总之，计算经纬度点到线段的最短距离是一个涉及多个领域知识的复杂问题，需要综合运用地理信息、数学、计算机等方面的知识来解决。
- 1 -。
MapInfo给定经纬度圈距离内的坐标简介MapInfo是一款地理信息系统软件，用于管理、分析和展示地理空间数据。
在MapInfo中，我们可以通过给定的经纬度和距离，找到位于圆圈内的坐标点。
本文将介绍如何使用MapInfo来实现这个功能，并提供详细的步骤和示例。
步骤步骤1：准备数据在开始之前，我们需要准备一些地理空间数据。
这些数据可以是点、线或面的数据，其中每个要素都有一个对应的经纬度坐标。
我们可以使用MapInfo自带的示例数据，或者导入自己的地理数据。
步骤2：创建查询在MapInfo中，我们可以使用SQL查询来筛选出满足特定条件的要素。
为了找到位于给定经纬度圆圈内的坐标点，我们需要使用距离函数来计算每个要素与给定经纬度的距离，并将结果与给定的半径进行比较。
以下是一个示例查询语句：SELECT * FROM表名WHERE Distance(经度列, 纬度列, 给定经度, 给定纬度, "km") <=给定半径在上述查询语句中，我们使用了Distance函数来计算每个要素与给定经纬度的距离，并将结果以千米为单位进行比较。
我们还使用了WHERE子句来筛选出满足距离条件的要素。
步骤3：运行查询在编写完查询语句后，我们可以将其运行在MapInfo的查询工具中。
首先，打开查询工具，然后将查询语句粘贴到查询编辑器中，并点击运行按钮。
MapInfo将会在地图上显示满足条件的要素。
步骤4：结果展示一旦查询运行完毕，MapInfo会在地图上显示满足条件的要素。
我们可以使用不同的符号和颜色来区分不同的要素，以便更好地展示结果。
此外，MapInfo还提供了一些工具和选项，可以对结果进行进一步的分析和处理。
示例为了更好地理解上述步骤，我们将使用一个示例来演示如何在MapInfo中找到给定经纬度圆圈内的坐标点。
假设我们有一个地理数据表，其中包含了一些城市的经纬度信息。
我们想要找到离给定经纬度(31.23, 121.47)半径为10公里的城市。
文章主要分为以下几个部分：一、概述1. 介绍python是一种流行的编程语言，广泛应用于数据处理、数据分析等领域。
2. 说明经纬度点到多边形区域最短距离的问题，以及相关性和实际应用。
二、相关概念和原理1. 解释经纬度的含义和表示方法。
2. 讲解多边形区域的概念和特点。
3. 介绍最短距离的定义和计算方法。
三、python实现1. 说明python的优势和适用性。
2. 介绍python常用的地理信息处理库和相关函数。
3. 给出用python实现经纬度点到多边形区域最短距离的具体方法和步骤。
四、实际案例分析1. 给出一个具体的实际案例。
2. 运用python实现经纬度点到多边形区域最短距离的计算，并展示结果。
3. 分析结果的意义和价值。
五、总结1. 总结python实现经纬度点到多边形区域最短距离的方法和步骤。
2. 强调python在地理信息处理方面的优势和应用前景。
3. 展望未来python在地理信息处理方面的发展方向。
在文章的撰写过程中，需要结构清晰，逻辑严谨，在介绍相关概念和原理时要求言简意赅，不涉及复杂的数学和地理知识，而在python实现和实际案例分析时要求具体详细，以便读者能够清晰理解并复现。
文章的语言要求规范、准确，需要尽可能避免口语化和俚语，以保证文章的客观正式和易读性。
六、相关概念和原理1.1 经纬度的含义和表示方法经纬度是地球表面上用来标志位置的一种坐标系统。
经度是指地球表面上某点与本初子午线的夹角，以东、西两个方向表示；纬度是指地球表面上某点与赤道的夹角，以北、南两个方向表示。
在地理信息系统中，经度通常用字母"X"或"longitude"表示，纬度用字母"Y"或"latitude"表示。
经度的取值范围是-180°到+180°，纬度的取值范围是-90°到+90°。
已知经纬度，求两地的距离 - 附“两地距离计算器”2011-07-26 11:01式中：α和θ分别是两地的纬度，北纬记为正，南纬记为负；β是两地的经度差；r是地球半径。
忽略各地海拔高度差异，认为地球是理想的球面。
求出的L 是两地的直线距离（地球的一条弦长），l 是两地的球面距离（沿地球表面的弧长）。
线性文本：k=√((sinθ-sinα )^2+(cosθ-cosα cosβ )^2+(cos α sinβ )^2；L=rk，l=2r sin^(-1)〖k/2〗公式注：arcsin得弧度值公式是我自己推导的。
式中的α和θ地位等价。
公式应用举例：求北京和悉尼之间的距离。
北京：39°54′57″N , 116°23′26″E悉尼：33°51′35.9″S , 151°12′40″E则：α=39°54′57″θ=－33°51′35.9″β=116°23′26″－151°12′40″=－34°49′14″代入公式中，查三角函数表，r取地球平均半径6371.004 千米，即可求得L = 8231.403 km l = 8949.214 km注意经度差的算法。
116°E和151°E相差151°-116°=35°，116°E和151°W相差360°-151°-116°=93°经度差35°或－35°或325°是等价的。
附两地距离计算器：此UI延续我造某的一贯风格。
比较易懂，操作说明我就不写了；如有问题可在本文下留言或联系我li.zaodie@。
下载地址：Distance.exe /self.aspx/z aodiesoft/distance.exe。
坐标距离计算器软件有哪些在现代社会的日常生活中，我们经常需要计算地球上不同坐标之间的距离。
这种需求在旅行、物流、导航等领域非常常见。
为了满足这种需求，许多坐标距离计算器软件被开发出来。
这些软件通过输入坐标信息，可以帮助我们计算出两个坐标之间的距离。
以下是一些常见的坐标距离计算器软件。
1. Google 地图作为全球最受欢迎的地图服务之一，Google 地图不仅可以提供导航和定位功能，还可以帮助用户计算两个坐标之间的距离。
通过在 Google 地图上输入两个地点的经纬度信息，用户可以获取它们之间的直线距离。
2. 百度地图百度地图是中国最受欢迎的在线地图服务。
类似于 Google 地图，它也可以用于计算两个坐标之间的距离。
用户可以使用百度地图的导航工具，输入坐标信息并获取它们之间的直线距离。
3. 腾讯地图腾讯地图是另一个在中国广泛使用的地图服务。
它也提供了坐标距离计算器的功能，用户可以通过在腾讯地图中输入两个地点的经纬度来计算它们之间的距离。
4. GPS 距离测量器GPS 距离测量器是一款专门用于测量地球上两个坐标之间距离的应用程序。
该应用可以通过使用设备的 GPS 功能获取当前位置，并允许用户手动输入另一个位置的坐标。
它会立即计算和显示两个坐标之间的距离。
5. 科学计算器类应用程序除了专门用于计算坐标距离的软件，一些科学计算器类应用程序也提供了坐标距离计算的功能。
这些应用程序通常具有更多的功能，例如单位转换、数学运算等。
用户可以通过在这些应用程序中输入坐标信息，获取它们之间的距离。
6. 在线坐标距离计算器网站除了使用手机应用程序，用户还可以使用在线坐标距离计算器网站来计算两个坐标之间的距离。
这些网站通常提供一个简单的界面，允许用户输入经纬度，并在提交后显示距离。
一些常见的在线坐标距离计算器网站包括 geoJS、GPSVisualizer和 GPS 根据地。
总结起来，随着科技的不断发展，我们有了许多方便计算坐标距离的选择。
标题： 如何使用excel 表计算两个经纬度之间的距离
序号： S C0000511175
资料类别 ： 案例库
质量等级： C 更新时间： 2009-06-04 13:56:32
阅读次数： 179
作者： 黎瑶
产品族： 无线性能和网规网优
产品： 网规网优工具
故障类别： 其他
关键字： E xcel 经纬度 距离
现象描述： 某项目进行站点勘测的时候，发现分包商反馈的站点经纬度与客户提供的经纬度距离不一致，需要量化计算两个经纬度之间的距离
告警
信息：
无
原因分析： 根据几何原理，设两点A 、B 的经、纬度分别为(jA,wA)(jB,wB)，则半径为R 的球面上两点间的
最短距离(大圆弧)为：
弧
AB=R*arccos[sin(wA)sin(wB)+cos(wA)cos(wB)*cos(jA-jB)]=R*ACOS(COS(jA-jB)*COS(wA-wB))
处理过程： 1、 制作一个excel 表，输入A 点和B 点的经纬度（十进制）。
2、 地球半径取值6370公里。
3、 利用RADIANS()函数把十进制的经纬度转化弧度。
4、 所以在excel 表的经纬度计算公式应该为
d=6370*ACOS(COS(RADIANS(jA)-RADIANS(jB))*COS(RADIANS(wA)-RADIANS(wB)))。
单位：KM
5、 注意：输入经纬度格式必须为十进制，输出结果为公里，结算结果误差在20米之内，基本满足站点勘测的使用。
Excel中批量返回经纬度距离的最小差值在日常的工作中，我们经常会遇到需要计算多个地点之间的距离的情况。
在物流行业中需要计算不同仓库之间的距离，或者在旅行规划中需要计算不同景点之间的距离。
而在Excel中，我们可以利用公式来进行这样的计算。
本文将介绍如何在Excel中批量返回经纬度距离的最小差值，以及如何利用这个功能进行实际的数据分析。
1. 理解经纬度我们需要了解经纬度这个概念。
经纬度是地球上任意一点的准确坐标，用来表示地球表面的位置。
经度是指东西方向的角度，位于赤道以东的经度被定义为正值，位于赤道以西的经度被定义为负值。
纬度是指南北方向的角度，赤道被定义为0度，南纬为负值，北纬为正值。
在Excel中，我们通常将经度表示为X轴上的值，纬度表示为Y轴上的值。
2. 计算两点之间的距离在Excel中，我们可以利用haversine公式来计算两个地点之间的距离。
这个公式基于经纬度来计算地球上任意两点之间的最短距离，是一种精确而有效的方法。
通过将两个地点的经纬度作为输入，我们可以利用这个公式来计算它们之间的距离。
在Excel中，我们可以使用自定义函数或者VBA代码来实现这一计算。
3. 批量返回距离的最小差值接下来，我们需要批量处理多个地点之间的距离，并返回它们之间的最小差值。
在Excel中，我们可以利用数组公式来实现这一功能。
我们将多个地点的经纬度输入到Excel表格中，然后利用haversine公式计算它们之间的距离。
我们可以使用MIN函数来找到这些距离中的最小值，从而返回最小差值。
4. 实际数据分析通过以上步骤，我们可以在Excel中批量返回经纬度距离的最小差值。
这个功能在实际的数据分析中非常有用。
在物流行业中，我们可以利用这个功能来找到距离最近的仓库，以优化货物的配送路线；在旅行规划中，我们可以利用这个功能来找到距离最近的景点，从而节省旅行时间。
通过对多个地点之间的距离进行全面的计算和比较，我们可以更好地理解它们之间的空间关系，为实际的决策提供支持。
经纬度定位查询系统简介经纬度定位是一种通过经度和纬度来确定地理位置的方法。
经度表示位置在东西方向上的距离，纬度表示位置在南北方向上的距离。
经纬度定位查询系统是一种基于经纬度坐标信息的位置查询工具，可以根据经纬度坐标快速准确地确定位置信息。
功能经纬度定位查询系统提供以下功能：1.坐标转换：将经纬度坐标与其他坐标系进行转换，如将经纬度坐标转换为UTM坐标、墨卡托投影坐标等，以满足不同应用场景的需求。
2.地址解析：根据经纬度坐标获取对应的地理位置信息，包括国家、省份、城市、街道等详细地址信息。
3.反向地址解析：根据地址信息查询对应的经纬度坐标，可以通过输入具体的地址信息来获取其对应的经纬度坐标。
4.距离计算：根据给定的两组经纬度坐标，计算它们之间的直线距离或者经过地球表面计算的路径距离。
5.区域检索：根据给定的经纬度坐标和搜索半径，在指定范围内检索符合条件的地址或者地点，如周边的餐馆、商店等。
应用场景经纬度定位查询系统在以下场景中有广泛应用：1.地图应用：通过经纬度定位查询系统，地图应用可以根据用户提供的经纬度坐标，准确地展示用户所在位置以及周边的地标和服务设施。
2.物流配送：在物流配送过程中，经纬度定位查询系统可以用于确定货物的具体位置，帮助企业实时掌握货物的运输状况。
3.旅游出行：通过经纬度定位查询系统，旅游者可以方便地获取自己当前所在位置的详细地址信息，并根据所在地点搜索周边的景点、餐馆、住宿等。
4.天气预报：经纬度定位查询系统可以与天气数据进行结合，根据用户所在位置的经纬度坐标提供该位置的天气预报信息。
使用方式经纬度定位查询系统可以通过以下方式使用：1.API接口：系统提供API接口，开发者可以通过调用接口实现经纬度的转换、地址解析、反向地址解析、距离计算等功能。
2.网页应用：系统提供网页版查询工具，用户可以直接在网页上输入经纬度或地址信息进行查询。
3.移动应用：系统提供移动应用程序，用户可以通过手机或平板设备进行经纬度定位查询。
