西安交通大学 材料力学总复习与习题课

材料力学复习题（一）一、1． B 2． B 3． A 、C 4． D5． A 、B 、D 6． C 7． A 、B 8． A 、B 、D 二、3.43-=xy τMPa ，3.43-''y x τMPa ，50='y σMPa三、3.254=BC Cr FkN ，45][=F kN四、略， 五、1.14-=Hx σMPa ，6.0=Hxz τ MPa ，2.143=r σMPa六、EIQl Ql EIh v Cd 94)41811(33++=材料力学复习题（二）一、选择题1、D ；2、B ；3、D ；4、C ；5、D 。

二、填空1、3段；位移边界条件 0,0,0===D A A w w θ；光滑连续条件CD C BC C w w ,,=，CD C BC C ,,θθ=，BC B AB B w w ,,=。

2、h y c 32=3、连续性假设；均匀性假设；各向同性假设；线弹性；小变形。

4、< ；= 。

5、0.003；0.002；47.12kN 。

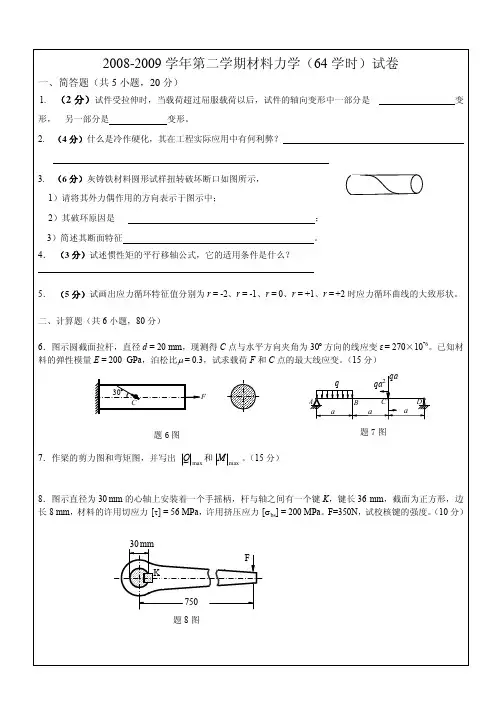
三、计算题1、图示为由五根直径50d mm =的圆形钢杆组成边长 为1a m =的正方形结构，材料为235Q 钢，比例极限aABC FaDF 题 3-1 图200p MPa σ=，屈服应力235s MPa σ=，弹性模量200E GPa =，中柔度杆的临界应力公式为304 1.12()cr MPa σλ=-。

试求该结构的许用载荷[]F 。

解：（1）求AB 、BD 和AD 杆的内力绘制节点A 和B 的受力图如图所示。

FF BAF DAA45ºF ABF BCF BDBAB 杆和AD 杆为受压杆，BD 杆受拉。

其内力分别为：2F F F AD AB ==，F F BD =（2）根据杆AB 和AD 的压杆稳定确定许可载荷圆杆4504mm d i ==，杆AB 和AD 的柔度均为805041000=⨯==mm i a μλ。

西安交通大学课程考试复习资料单选题1.设轴向拉伸杆横截面上的正应力为σ,则45o斜截面上的正应力和剪应力( )A.分别为σ/2和σB.均为σC.分别为σ和σ/2D.均为σ/2答案: D2.关于压杆临界力的大小,说法正确的答案是( )A.与压杆所承受的轴向压力大小有关B.与压杆的柔度大小有关C.与压杆所承受的轴向压力大小有关D.与压杆的柔度大小无关答案: B3.单位长度扭转角θ与( )无关A.杆的长度B.扭矩C.材料性质D.截面几何性质答案: A4.在以下措施中( )将会降低构件的持久极限A.增加构件表面光洁度B.增加构件表面硬度C.加大构件的几何尺寸D.减缓构件的应力集中答案: C5.在非对称循环应力下,材料的持久极限为σr=σa+σm,若构件的应力集中,表面质量和尺寸的综合影响系数为α,则构件的持久极限=( )A.σa+σmB.α(σa+σm)C.ασa+σmD.ασa+σm答案: C6.在相同的交变载荷作用下,构件的横向尺寸增大,其( )A.工作应力减小，持久极限提高B.工作应力增大，持久极限降低C.工作应力增大，持久极限提高D.工作应力减小，持久极限降低答案: D7.材料的持久极限与试件的( )无关A.材料B.变形形式C.循环特征D.最大应力答案: D8.关于理论应力集中系数α和有效应力集中系数Kσ有以下四个结论。

其中( )是正确的A.α与材料性质无关系，Kσ与材料性质有关系B.α与材料性质有关系，Kσ与材料性质无关系C.α和Kσ均与材料性质有关系D.α和Kσ均与材料性质无关系答案: A9.有效应力集中系数Kσ和尺寸系数εσ的数值范围分别为( )A.Kσ>1, εσ<1B.Kσ<1, εσ<1C.Kσ>1, εσ>1D.Kσ<1, εσ>1答案: A10.脆性材料的破坏应力是( )A.比例极限B.弹性极限C.屈服极限D.强度极限答案: D11.塑性材料的名义屈服应力使用( )A.σS表示B.σb表示C.σp表示D.σ0.2表示答案: D12.在冲击应力和变形实用计算的能量法中,因为不计被冲击物的质量,所以计算结果与实际情况相比,( )A.冲击应力偏大，冲击变形偏小B.冲击应力偏小，冲击变形偏大C.冲击应力和冲击变形均偏大D.冲击应力和冲击变形均偏小答案: C13.厚壁玻璃杯倒入开水发生破裂时,裂纹起始于( )A.内壁B.外壁C.壁厚的中间D.整个壁厚答案: B14.铸铁水管冬天结冰时会因冰膨胀而胀裂,而管内的冰不破碎,这是因为( )A.冰的强度比铸铁高B.冰的温度比铸铁高C.冰的应力相当小D.冰处于三向等压应力状态答案: D15.对于二向等拉的应力状态,除( )强度理论外,其他强度理论的相当应力都相等A.第一B.第二C.第三D.第四答案: B16.一受静水压力的小球,下列结论中错误的是( )A.球内各点的应力状态均为三向等压B.球内各点不存在切应力C.小球的体积应变为零D.小球的形状改变比能为零答案: C17.滚珠轴承中,滚珠和外圆接触点处的应力状态是( )应力状态A.单向B.二向C.三向D.纯剪切答案: C18.应用叠加原理求梁横截面的挠度、转角时,需要满足的条件有( )A.梁必须是等截面的B.梁必须是静定的C.变形必须是小变形D.梁的弯曲必须是平面弯曲答案: C19.非对称的薄壁截面梁承受横向力时,若要求梁只产生平面弯曲而不发生扭转,则横向力作用的条件是( )A.作用面与形心主惯性平面重合B.作用面与形心主惯性平面平行C.通过弯曲中心的任意平面D.通过弯曲中心，平行于主惯性平面答案: D20.梁发生平面弯曲时,其横截面绕( )旋转A.梁的轴线B.截面对称轴C.中性轴D.截面形心答案: C21.梁在某一段内作用有向下的分布力时,则在该段内M图是一条 ( )A.上凸曲线B.下凸曲线C.带有拐点的曲线D.斜直线答案: A22.梁在集中力偶作用的截面处,它的内力图为( )A.Q图有突变， M图无变化B.Q图有突变，M图有转折C.M图有突变，Q图无变化D.M图有突变，Q图有转折答案: C23.梁在集中力作用的截面处,它的内力图为( )A.Q图有突变， M图光滑连续B.Q图有突变，M图有转折C.M图有突变，Q图光滑连续D.M图有突变，Q图有转折24.描述构件上一截面变形前后的夹角叫( )A.线位移B.转角C.线应变D.角应变答案: B25.阶梯圆轴的最大切应力发生在( )A.扭矩最大截面B.直径最小的截面C.单位长度扭转角最大的截面D.不能确定答案: D26.应用拉压正应力公式σ=N/A的条件是( )A.应力小于比例极限B.外力的合力沿杆轴线C.应力小于弹性极限D.应力小于屈服极限答案: B27.滚珠轴承中,滚珠和外圆接触点处的应力状态是()应力状态。

材料力学复习题（一）一、1． B 2． B 3． A 、C 4． D5． A 、B 、D 6． C 7． A 、B 8． A 、B 、D二、3.43-=xy τMPa ，3.43-''y x τMPa ，50='y σMPa三、3.254=B C Cr F kN ，45][=F kN四、略， 五、1.14-=Hx σMPa ，6.0=Hxz τ MPa ，2.143=r σMPa六、EI Ql QlEIh v Cd 94)41811(33++=材料力学复习题（二）一、选择题1、D ；2、B ；3、D ；4、C ；5、D 。

二、填空1、3段；位移边界条件 0,0,0===D A A w w θ；光滑连续条件CD C BC C w w ,,=，CD C BC C ,,θθ=，BC B AB B w w ,,=。

2、h y c 32=3、连续性假设；均匀性假设；各向同性假设；线弹性；小变形。

4、< ；= 。

5、0.003；0.002；47.12kN 。

三、计算题1、图示为由五根直径50d mm =的圆形钢杆组成边长 为1a m =的正方形结构，材料为235Q 钢，比例极限aABC FaDF 题 3-1 图200p MPa σ=，屈服应力235s MPa σ=，弹性模量200E GPa =，中柔度杆的临界应力公式为304 1.12()cr MPa σλ=-。

试求该结构的许用载荷[]F 。

解：（1）求AB 、BD 和AD 杆的内力绘制节点A 和B 的受力图如图所示。

FF BAF DAA45ºF ABF BCF BDBAB 杆和AD 杆为受压杆，BD 杆受拉。

其内力分别为：2F F F AD AB ==，F F BD =（2）根据杆AB 和AD 的压杆稳定确定许可载荷圆杆4504mm d i ==，杆AB 和AD 的柔度均为805041000=⨯==mm i a μλ。

目录目录 (1)工程材料中原子排列 (2)参考答案 (4)固体中的相结构 (9)参考答案 (12)凝固 (16)参考答案 (19)相图 (25)参考答案 (38)固体中的扩散 (40)参考答案 (43)塑性变形 (45)参考答案 (48)回复与再结晶 (51)参考答案 (54)固体相变 (58)参考答案 (60)复合效应与界面 (64)参考答案 (66)工程材料中原子排列1. 作图表示立方晶体的()()()421,210,123晶面及[][][]346,112,021晶向。

2. 在六方晶体中，绘出以下常见晶向[][][][][]0121,0211,0110,0112,0001等。

3. 写出立方晶体中晶面族{100}，{110}，{111}，{112}等所包括的等价晶面。

4. 镁的原子堆积密度和所有hcp 金属一样，为0.74。

试求镁单位晶胞的体积。

已知Mg 的密度3Mg/m 74.1=m g ρ，相对原子质量为24.31，原子半径r=0.161nm 。

5. 当CN=6时+Na 离子半径为0.097nm ，试问：1) 当CN=4时，其半径为多少？2) 当CN=8时，其半径为多少？6. 试问：在铜（fcc,a=0.361nm ）的<100>方向及铁(bcc,a=0.286nm)的<100>方向,原子的线密度为多少？7. 镍为面心立方结构，其原子半径为nm 1246.0=Ni r 。

试确定在镍的（100），（110）及（111）平面上12mm 中各有多少个原子。

8. 石英()2SiO 的密度为2.653Mg/m 。

试问： 1) 13m 中有多少个硅原子（与氧原子）？2) 当硅与氧的半径分别为0.038nm 与0.114nm 时，其堆积密度为多少（假设原子是球形的）？9. 在800℃时1010个原子中有一个原子具有足够能量可在固体内移动，而在900℃时910个原子中则只有一个原子，试求其激活能（J/原子）。

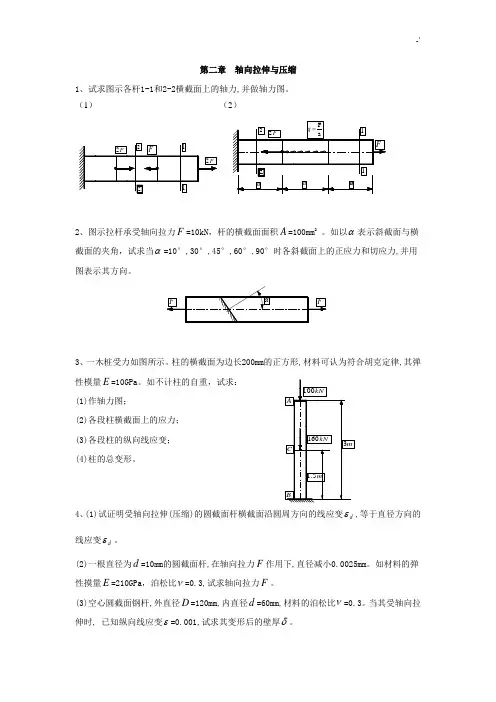
第二章 轴向拉伸与压缩1、试求图示各杆1-1和2-2横截面上的轴力,并做轴力图。

（1） （2）2、图示拉杆承受轴向拉力F =10kN ，杆的横截面面积A =100mm 2。

如以α表示斜截面与横截面的夹角，试求当α=10°,30°,45°,60°,90°时各斜截面上的正应力和切应力,并用图表示其方向。

3、一木桩受力如图所示。

柱的横截面为边长200mm 的正方形,材料可认为符合胡克定律,其弹性模量E =10GPa 。

如不计柱的自重，试求：(1)作轴力图；(2)各段柱横截面上的应力； (3)各段柱的纵向线应变；(4)柱的总变形。

4、(1)试证明受轴向拉伸(压缩)的圆截面杆横截面沿圆周方向的线应变d ε,等于直径方向的线应变d ε。

(2)一根直径为d =10mm 的圆截面杆,在轴向拉力F 作用下,直径减小0.0025mm 。

如材料的弹性摸量E =210GPa ，泊松比ν=0.3,试求轴向拉力F 。

(3)空心圆截面钢杆,外直径D =120mm,内直径d =60mm,材料的泊松比ν=0.3。

当其受轴向拉伸时, 已知纵向线应变ε=0.001,试求其变形后的壁厚δ。

5、图示A和B两点之间原有水平方向的一根直径d=1mm的钢丝,在钢丝的中点C加一竖直荷载F。

已知钢丝产生的线应变为ε=0.0035,其材料的弹性模量E=210GPa，钢丝的自重不计。

试求：(1) 钢丝横截面上的应力(假设钢丝经过冷拉,在断裂前可认为符合胡克定律)；(2) 钢丝在C点下降的距离∆；(3) 荷载F的值。

6、简易起重设备的计算简图如图所示.一直斜杆AB应用两根63mm×40mm×4mm不等边角钢组[σ=170MPa。

试问在提起重量为P=15kN的重物时,斜杆AB是否满足强度成,钢的许用应力]条件?7、一结构受力如图所示,杆件AB,AD均由两根等边角钢组成。

已知材料的许用应力[σ=170MPa，试选择杆AB,AD的角钢型号。

王奥运土木工程（10）班材料力学学习指导与练习第一章绪论1.1预备知识一、基本概念1、构件工程中遇到的各种建筑物或机械是由若干部件(零件)组成的。

这些部件(零件)称为构件，根据其几何特征可分为：杆件、板、块体和薄壁杆件等。

其中杆件是本课程的研究对象。

2、承载能力要保证建筑物或机械安全地工作，其组成的构件需安全地工作，即要有足够的承受载荷的能力，这种承受载荷的能力简称承载能力。

在材料力学中，构件承载能力分为三个方面：(1)强度：构件抵抗破坏的能力。

(2)刚度：构件抵抗变形的能力。

(3)稳定性：构件保持原有平衡形式的能力。

3、材料力学的任务在保证构件既安全适用又尽可能经济合理的前提下，为构件的设计提供理论依据和计算方法。

而且，还在基本概念、理论和方法等方面，为结构力学、弹性力学、钢筋混凝土、钢结构等后续课程提供基础。

4、变形固体的基本假设建筑物、机械等的各种构件都是由各种固体材料制成的，在载荷的作用下都会发生尺寸和形状的变化，因此在材料力学研究的构件都是变形固体。

而且为了简化计算，对变形固体作了如下假设：(1)连续性假设即认为物体在其整个体积内毫无空隙地充满了物质。

(2)均匀性假设即认为扬物体在其整个体积内材料的结构和性质相同。

(3)各向同性假没即认为物体在各个方向具有相同的性质。

5、内力、截面法和应力(1)材料力学研究的内力是外部因素(载荷作用、温度变化、支座沉降等)引起构件不同部分之间相互作用力的变化。

(2)用假想截面将构件截开为两部分，取其中任一部分利用静力平衡方程求解截面上内力的方法称为截面法，是材料力学求解内力的基本方法。

(3)内力的面积分布集度称为应力，单位是：N/m(Pa)、MN/m(MPa)。

应力是一个矢量，垂直于截面的分量称为正应力，用表示；切于截面的分量称为剪应力，同表示。

6、变形、位移及应变(1)构件在外力作用下会发生尺寸和形状的改变，称为变形。

(2)变形会使构件上各点、各线和各面的空间位置发生移动，称为位移。

材料⼒学学习指导与练习材料⼒学学习指导与练习第⼆章2.1预备知识⼀、基本概念1、轴向拉伸与压缩承受拉伸或压缩杆件的外⼒作⽤线与杆轴线重合，杆件沿杆轴线⽅向伸长或缩短，这种变形形式称为轴向拉伸或轴向压缩。

2、轴⼒和轴⼒图轴向拉压杆的内⼒称为轴⼒，⽤符号F N 表⽰。

当F N 的⽅向与截⾯外向法线⽅向⼀致时，规定为正，反之为负。

求轴⼒时仍然采⽤截⾯法。

求内⼒时，⼀般将所求截⾯的内⼒假设为正的数值，这⼀⽅法称为“设正法”。

如果结果为正，则说明假设正确，是拉⼒；如是负值，则说明假设错误，是压⼒。

设正法在以后求其他内⼒时还要到。

为了形象的表明各截⾯轴⼒的变化情况，通常将其绘成“轴⼒图”。

作法是：以杆的左端为坐标原点，取χ轴为横坐标轴，称为基线，其值代表截⾯位置，取F N 轴为纵坐标轴，其值代表对应截⾯的轴⼒值，正值绘在基线上⽅，负值绘在基线下⽅。

3、横截⾯上的应⼒根据圣维南(Saint-V enant)原理，在离杆⼀定距离之外，横截⾯上各点的变形是均匀的，各点的应⼒也是均匀的，并垂直于横截⾯，即为正应⼒，设杆的横截⾯⾯积为A ，则有AN =σ正应⼒的符号规则：拉应⼒为正，压应⼒为负。

4、斜截⾯上的应⼒与横截⾯成α⾓的任⼀斜截⾯上，通常有正应⼒和切应⼒存在，它们与横截⾯正应⼒σ的关系为：()=+=αστασσαα2sin 22cos 12α⾓的符号规则：杆轴线x 轴逆时针转到α截⾯的外法线时，α为正值；反之为负。

切应⼒的符号规则：截⾯外法线顺时针转发900后，其⽅向和切应⼒相同时，该切应⼒为正值；反之为负值。

当α=00时，正应⼒最⼤，即横截⾯上的正应⼒是所有截⾯上正应⼒中的最⼤值。

当α=±450时，切应⼒达到极值。

5、轴向拉伸与压缩时的变形计算与虎克定律（1）等直杆受轴向拉⼒F 作⽤，杆的原长为l ，⾯积为A ，变形后杆长由l 变为l +?l ，则杆的轴向伸长为EAFl l =⽤内⼒表⽰为EAl l N F =上式为杆件拉伸（压缩）时的虎克定律。

(单选题)1.关于压杆临界力的大小,说法正确的答案是( ) A: 与压杆所承受的轴向压力大小有关
B: 与压杆的柔度大小有关
C: 与压杆所承受的轴向压力大小有关
D: 与压杆的柔度大小无关
正确答案: B
(单选题)2.判断下列结论正确的是( )
A: 杆件某截面上的内力是该截面上应力的代数和
B: 杆件某截面上的应力是该截面上内力的平均值
C: 应力是内力的集度
D: 内力必大于应力
正确答案: C
(单选题)3.单位长度扭转角θ与( )无关
A: 杆的长度
B: 扭矩
C: 材料性质
D: 截面几何性质
正确答案: A
(单选题)4.扭转切应力公式适用于( )杆件
A: 任意截面
B: 任意实心截面
C: 任意材料的圆截面
D: 线弹性材料的圆截面
正确答案: D
(单选题)5.在以下措施中( )将会降低构件的持久极限A: 增加构件表面光洁度
B: 增加构件表面硬度
C: 加大构件的几何尺寸
D: 减缓构件的应力集中
正确答案: C
(单选题)6.材料的持久极限与试件的( )无关
A: 材料
B: 变形形式
C: 循环特征。