第七章 土坡稳定分析
- 格式:doc
- 大小:240.51 KB
- 文档页数:7


第七章土坡稳定分析土坡的稳定性是指土坡在自身重力和外部荷载作用下,能够保持不发生倾覆、滑动或坍塌的能力。
土坡的稳定性分析是土坡工程设计的关键步骤之一,它的目的是确定土体的最大稳定角,以及土坡所能承受的最大荷载。
土坡稳定性分析主要包括以下几个方面:1.荷载计算:首先需要确定土坡所受到的各种荷载,包括自重荷载、地震荷载、水压力荷载等。
这些荷载将直接影响土坡的稳定性。
2.土体力学参数:土坡的稳定性分析需要确定土体的力学参数,包括土体的内摩擦角、剪胀角、孔隙比等。
这些参数可以通过室内试验或现场试验来确定。
3.土体抗剪强度:土坡的稳定性分析需要确定土体的抗剪强度,包括黏聚力和内摩擦角。
一般可通过室内试验或相关经验公式来确定。
4.平衡条件:土坡的稳定性分析需要确定土坡的平衡条件,即坡面上的剪切力与抗剪强度之间的平衡关系。
通过平衡条件,可以计算出土坡的最大稳定角。
5.稳定性判据:土坡的稳定性分析需要选择适当的稳定性判据,以判断土坡是否稳定。
常用的稳定性判据包括平衡法、极限平衡法、有限元法等。
在进行土坡稳定性分析时,需要注意以下几个问题:1.考虑边界条件:土坡的稳定性分析需要考虑土坡周围的边界条件,包括土坡顶部的固结载荷、土坡脚部的支撑条件等。
2.考虑不同荷载组合:土坡的稳定性分析需要考虑不同荷载组合的影响,包括常规和临界荷载组合。
常规荷载组合是指常规工况下土坡所承受的荷载组合,临界荷载组合是指在其中一特定条件下土坡的最不利工况下所承受的荷载组合。
3.安全系数:土坡的稳定性分析需要根据土坡的设计要求和实际情况,确定相应的安全系数。
安全系数是指土坡的稳定强度与设计要求强度之间的比值,一般要求安全系数大于14.考虑时间因素:土坡的稳定性分析需要考虑土体的变形和固结过程。
在长期静荷载作用下,土体可能发生蠕变和沉降等变形。
因此,在进行土坡稳定性分析时,需要考虑时间因素的影响。
综上所述,土坡的稳定性分析是土坡工程设计中一个非常重要的环节。
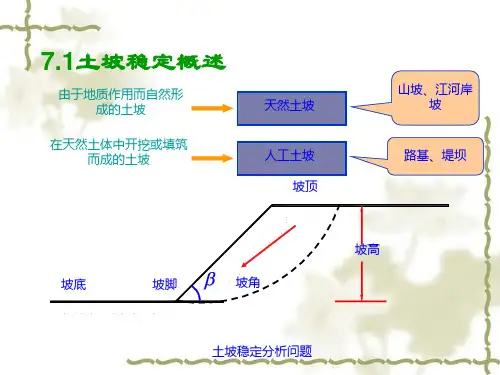

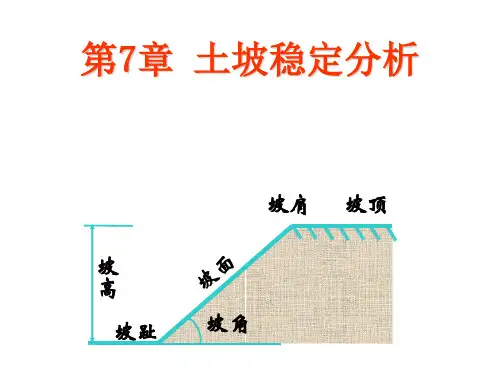
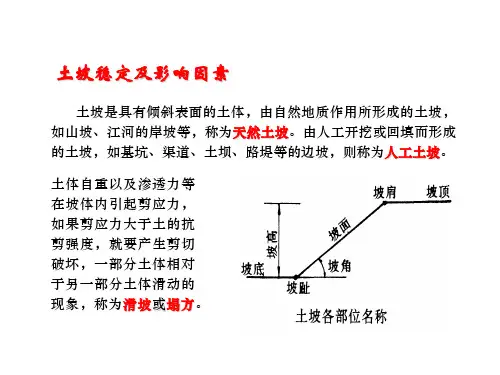
第七章土坡稳定性分析第一节概述土坡就是由土体构成、具有倾斜坡面的土体,它的简单外形如图7-1所示。
一般而言,土坡有两种类型。
由自然地质作用所形成的土坡称为天然土坡,如山坡、江河岸坡等;由人工开挖或回填而形成的土坡称为人工土(边)坡,如基坑、土坝、路堤等的边坡。
土坡在各种内力和外力的共同作用下,有可能产生剪图7-1 土坡各部位名称切破坏和土体的移动。
如果靠坡面处剪切破坏的面积很大,则将产生一部分土体相对于另一部分土体滑动的现象,称为滑坡。
土体的滑动一般系指土坡在一定范围内整体地沿某一滑动面向下和向外移动而丧失其稳定性。
除设计或施工不当可能导致土坡的失稳外,外界的不利因素影响也触发和加剧了土坡的失稳,一般有以下几种原因:1.土坡所受的作用力发生变化:例如,由于在土坡顶部堆放材料或建造建筑物而使坡顶受荷。
或由于打桩振动,车辆行驶、爆破、地震等引起的振动而改变了土坡原来的平衡状态;2.土体抗剪强度的降低:例如,土体中含水量或超静水压力的增加;3.静水压力的作用:例如,雨水或地面水流入土坡中的竖向裂缝,对土坡产生侧向压力,从而促进土坡产生滑动。
因此,粘性土坡发生裂缝常常是土坡稳定性的不利因素,也是滑坡的预兆之一。
在土木工程建筑中,如果土坡失去稳定造成塌方,不仅影响工程进度,有时还会危及人的生命安全,造成工程失事和巨大的经济损失。
因此,土坡稳定问题在工程设计和施工中应引起足够的重视。
天然的斜坡、填筑的堤坝以及基坑放坡开挖等问题,都要演算斜坡的稳定性,亦既比较可能滑动面上的剪应力与抗剪强度。
这种工作称为稳定性分析。
土坡稳定性分析是土力学中重要的稳定分析问题。
土坡失稳的类型比较复杂,大多是土体的塑性破坏。
而土体塑性破坏的分析方法有极限平衡法、极限分析法和有限元法等。
在边坡稳定性分析中,极限分析法和有限元法都还不够成熟。
因此,目前工程实践中基本上都是采用极限平衡法。
极限平衡方法分析的一般步骤是:假定斜坡破坏是沿着土体内某一确定的滑裂面滑动,根据滑裂土体的静力平衡条件和莫尔—库伦强度理论,可以计算出沿该滑裂面滑动的可能性,即土坡稳定安全系数的大小或破坏概率的高低,然后,再系统地选取许多个可能的滑动面,用同样的方法计算其稳定安全系数或破坏概率。



第七章:土坡的稳定性分析关于土坡分析时的几个名词砂性土的土坡稳定分析现有一砂性土土坡,剖面如图所示,其上有一个砂土粒,自重为W ,自重在垂直于坡面方向的分力为G .cos α,沿着坡面方向分力G . sin α,土粒在自重作用下沿坡面下滑,土粒与坡面之间的摩擦力阻止下滑;按力学概念抗滑移力:S=N.tan ϕ=W.cos α.tan ϕ滑移力:T=W.sin α两者的比值为滑移稳定安全系数。
K 稳定安全系数:当 K>1时 稳定 即ϕ>aK<1时 失稳 即ϕ<a K=1时 临界状态 即ϕ=a结论:也就是说,砂性土的土坡稳定与否与坡高H 无关,仅取决于土的内摩擦角ϕ和坡角α的比值。
粘性土土坡稳定分析——------瑞典条分法设有一粘性土土坡,按比例画出土坡剖面如图,任选一点o 为圆心,过坡脚A 作圆弧AC ,设土坡沿AC 弧滑动;将AC 弧上的土体分成n 个宽度相等的小土条。
取出其中的第i 个小土条,进行受力分析,第i 个小土条共受有: 1.土条自重Wi ,方向向下,作用在小土条形心处, 其值等于r*∆V ,其中的r 为第i 个小土条土的容重,∆Vi 为第i 个小土条体积,在该土条宽度内有外荷载Q i 时,还应加上外荷载Q i , 2.左右两个侧面上的作用力H i 、E i 、H i+1和E i+1。
3.滑动面上的力N i 和抗剪强度S i :其中N i = (W i +Q i )*cos i α,S i = N i * tan φi + c i *∆L i c i ~第i 个小土条土的内聚力,ΔL i ~第i 个小土条的弧长,αi ~第i 个小土条中点处切线的水平倾角当土条宽度较小时,可忽略土条侧面上的作用力H i 、E i 、H i+1和E i+1;此时,土条上各力对圆心点O的抗滑力矩Msi 和滑移力矩M i 分别为:Msi = R *S i = R *( N i * tanφi +c i ∆L i ),M i =R* W i *sin i α。
第七章土坡稳定性分析第一节概述土坡就是由土体构成、具有倾斜坡面的土体,它的简单外形如图7-1所示。
一般而言,土坡有两种类型。
由自然地质作用所形成的土坡称为天然土坡,如山坡、江河岸坡等;由人工开挖或回填而形成的土坡称为人工土(边)坡,如基坑、土坝、路堤等的边坡。
土坡在各种内力和外力的共同作用下,有可能产生剪图7-1 土坡各部位名称切破坏和土体的移动。
如果靠坡面处剪切破坏的面积很大,则将产生一部分土体相对于另一部分土体滑动的现象,称为滑坡。
土体的滑动一般系指土坡在一定范围内整体地沿某一滑动面向下和向外移动而丧失其稳定性。
除设计或施工不当可能导致土坡的失稳外,外界的不利因素影响也触发和加剧了土坡的失稳,一般有以下几种原因:1.土坡所受的作用力发生变化:例如,由于在土坡顶部堆放材料或建造建筑物而使坡顶受荷。
或由于打桩振动,车辆行驶、爆破、地震等引起的振动而改变了土坡原来的平衡状态;2.土体抗剪强度的降低:例如,土体中含水量或超静水压力的增加;3.静水压力的作用:例如,雨水或地面水流入土坡中的竖向裂缝,对土坡产生侧向压力,从而促进土坡产生滑动。
因此,粘性土坡发生裂缝常常是土坡稳定性的不利因素,也是滑坡的预兆之一。
在土木工程建筑中,如果土坡失去稳定造成塌方,不仅影响工程进度,有时还会危及人的生命安全,造成工程失事和巨大的经济损失。
因此,土坡稳定问题在工程设计和施工中应引起足够的重视。
天然的斜坡、填筑的堤坝以及基坑放坡开挖等问题,都要演算斜坡的稳定性,亦既比较可能滑动面上的剪应力与抗剪强度。
这种工作称为稳定性分析。
土坡稳定性分析是土力学中重要的稳定分析问题。
土坡失稳的类型比较复杂,大多是土体的塑性破坏。
而土体塑性破坏的分析方法有极限平衡法、极限分析法和有限元法等。
在边坡稳定性分析中,极限分析法和有限元法都还不够成熟。
因此,目前工程实践中基本上都是采用极限平衡法。
极限平衡方法分析的一般步骤是:假定斜坡破坏是沿着土体内某一确定的滑裂面滑动,根据滑裂土体的静力平衡条件和莫尔—库伦强度理论,可以计算出沿该滑裂面滑动的可能性,即土坡稳定安全系数的大小或破坏概率的高低,然后,再系统地选取许多个可能的滑动面,用同样的方法计算其稳定安全系数或破坏概率。
第七章土坡稳定分析第七章土坡稳定分析第一节概述土坡就是具有倾斜坡面的土体(图7-l )。
由自然地质作用所形成的土坡称为天然土坡。
由人工开挖或回填而形成的土坡则称为人工土坡。
土体重量以及渗透力等在坡体内引起剪应力,如果剪应力大于土的抗剪强度,就要产生剪切破坏。
如果靠坡面处剪切破坏的面积很大,则将产生一部分土体相对于另一部分土体滑动的现象,这一现象称为滑坡。
滑坡可分为半无限长滑坡和有限长滑坡。
半无限长滑坡是指滑动坡面的长度比滑坡深度大很多,成大平板形状的滑动(图7-2a ),而有限长滑坡是指滑动面的长度与滑坡深度的尺度相当(图7-2b )。
粗粒土中的滑坡,一般为深度较浅而形状接近于平面或者由两个以上平面组成的折线形滑动面。
粘性土中的滑坡深入坡体内,均质粘性土坡滑动面的形状为对数螺线曲面,在计算中通常以圆弧面代替(图7-3)。
土石坝是常见的大型人工土坡,它是近代坝工建筑中广泛应用的一种坝型。
目前土石坝的坝高已达到300m 以上。
高土石坝的土石方量巨大,因此选择安全可靠而又经济合理的断面就是一个十分重要的问题。
一座高100m 的土坝(图7-6),如果上、下游坝坡能从1:2.5减小到1:2.0,每一延米断面可节省土方量5000m 3。
一公里坝长就可节省土方500万rn 3,这是一个巨大的工程量。
然而能否节省取决于边坡是否能保持稳定。
因此,土坝边坡稳定分析是土石坝设计中的一项重要的内容。
在边坡稳定分析中,目前工程实践中基本上都是采用极限平衡法。
极限平衡法的一般步骤是先假定破坏是沿土体内某一确定的滑动面滑动,根据滑裂土体的静力平衡条件和摩尔-库伦破坏准则计算沿该滑裂面滑动的可能性,即安全系数的大小,然后系统地选取多个可能的滑动面,用同样方法计算稳定安全系数或破坏概率。
安全系数最低或破坏概率最高的滑动面就是可能性最大的滑动面。
第二节无粘性土坡的稳定分析一、均质干坡和水下坡均质干坡和水下坡指由一种土组成、完全在水位以上或完全在水位以下,没有渗透水流作用的无粘性土坡。
第七章 土坡稳定分析第一节 概述土坡就是具有倾斜坡面的土体(图7-l )。
由自然地质作用所形成的土坡称为天然土坡。
由人工开挖或回填而形成的土坡则称为人工土坡。
土体重量以及渗透力等在坡体内引起剪应力,如果剪应力大于土的抗剪强度,就要产生剪切破坏。
如果靠坡面处剪切破坏的面积很大,则将产生一部分土体相对于另一部分土体滑动的现象,这一现象称为滑坡。
滑坡可分为半无限长滑坡和有限长滑坡。
半无限长滑坡是指滑动坡面的长度比滑坡深度大很多,成大平板形状的滑动(图7-2a ),而有限长滑坡是指滑动面的长度与滑坡深度的尺度相当(图7-2b )。
粗粒土中的滑坡,一般为深度较浅而形状接近于平面或者由两个以上平面组成的折线形滑动面。
粘性土中的滑坡深入坡体内,均质粘性土坡滑动面的形状为对数螺线曲面,在计算中通常以圆弧面代替(图7-3)。
土石坝是常见的大型人工土坡,它是近代坝工建筑中广泛应用的一种坝型。
目前土石坝的坝高已达到300m 以上。
高土石坝的土石方量巨大,因此选择安全可靠而又经济合理的断面就是一个十分重要的问题。
一座高100m 的土坝(图7-6),如果上、下游坝坡能从1:2.5减小到1:2.0,每一延米断面可节省土方量5000m 3。
一公里坝长就可节省土方500万rn 3,这是一个巨大的工程量。
然而能否节省取决于边坡是否能保持稳定。
因此,土坝边坡稳定分析是土石坝设计中的一项重要的内容。
在边坡稳定分析中,目前工程实践中基本上都是采用极限平衡法。
极限平衡法的一般步骤是先假定破坏是沿土体内某一确定的滑动面滑动,根据滑裂土体的静力平衡条件和摩尔-库伦破坏准则计算沿该滑裂面滑动的可能性,即安全系数的大小,然后系统地选取多个可能的滑动面,用同样方法计算稳定安全系数或破坏概率。
安全系数最低或破坏概率最高的滑动面就是可能性最大的滑动面。
第二节 无粘性土坡的稳定分析一、均质干坡和水下坡均质干坡和水下坡指由一种土组成、完全在水位以上或完全在水位以下,没有渗透水流作用的无粘性土坡。
这两种情况只要坡面上的土颗粒在重力作用下能够保持稳定,整个土坡就处于稳定状态。
从砂堆坡面上取一小块土体来分析它的稳定条件图(7-7a )。
设小土体的重量为W ,W 沿坡面的滑动力αsin W T =。
垂直于坡面的正压力αcos W N =,正压力产生摩擦阻力,阻抗土体下滑,称抗滑力,其值为φαφtg W Ntg R ∙==cos (库伦定理)。
定义土体的稳定安全系数F s 为:1)-(7 sin cos tgatg a W tg a W T R F s φφ=∙===滑动力抗滑力 式中,φ—土的内摩擦角(0);α—土的坡度角(0)式(7-1)与土坡的高度无关,因此安全系数F s 代表整个边坡的安全度。
当Fs=1时,α=φ,α称为天然休止角,其值等于砂在松散状态时的内摩擦角。
如是经过压密后的无粘性土,内摩擦角增大,稳定坡角也随之增大。
二、有渗透水流的均质土坡挡水土堤内形成渗流场,如果浸润线在下游坡面逸出,这时在浸润线以下,下游坡内的土体除受重力作用外,还受渗透力的作用,因而会降低下游边坡的稳定性。
先分析浸润线逸出点以下部分边坡的稳定性(图7-8)。
如果水流的方向与水平面成夹角θ,则沿水流方向的渗透力i j w γ=。
在坡面上取土体V 中的土骨架为隔离体,其有效重量为V 'γ。
分析这块土骨架的稳定性,作用在土骨架上的总渗透力为iV jV J w γ==。
沿坡内的全部滑动力,包括重力和渗透力,为)cos(sin θαγαγ-+'=iV V T w坡面的正压力为)sin(cos θαγαγ--'=iV V N w土体沿坡面滑动的稳定安全系数2)-(7 )cos(sin )]sin(cos [θαγαγφθαγαγφ-+'--'==iV V tg iV V T Ntg F w w s 式中,i —渗透坡降;γ'—土体的浮容重;w γ—水的容重;φ—土的内摩擦角。
若水流在逸出段顺坡面流动,即αθ=。
这时,流经途径ds 的水头损失为dh ,故有3)-(7 sin sin αθ===dsdh i 将式(7-2)和0=-αθ条件代入式(7-2),得4)-(7 sin cos sin sin cos ''''αφγγαγφαγααγφαγtg tg tg V r V tg V F sat sat w s ∙=∙=+∙= 由此可见,当逸出段为顺坡渗流时,安全系数降低sat γγ'倍,通常satγγ'约为0.5,即安全系数降低一半。
因此要保持同样的安全度,有渗流逸出时的坡角比没有渗流逸出时(式(7-1))的要平缓得多。
为了使设计经济全理,工程上一般要在下游坝址处设置排水棱体,使渗透水流不直接从下游坡面逸出(图7-9)。
这时下游坡面虽然没有浸润线逸出,但下游坡内、浸润线以下的土体仍然受渗透力的作用。
这种渗透力是一种滑动力,它将降低从浸润线以下通过的滑动面的稳定性。
这时深层滑动面(如图7-9中虚线所示)的稳定性可能比下游坡面的稳定性差,即危险的滑动面向深层发展。
这种情况下,除了要按前述方法验算坡面的稳定性外,还应该用圆弧滑动法验算深层滑动的可能性。
三、部分浸水土坡当水库部分蓄水时,水位以上是干坡,水位以下则是浸水坡。
水位上下,土的容重从天然容量变成浮容重。
如果水位上下土的内摩擦角不变(式(7-1)),则整个坡面主体的稳定性相同。
但对于深入坡内的滑动面(图7-10a 中的ADC 面),由于滑动土体上部的容重大,滑动力大;下部的容重小,抗滑力小,显然稳定性比干坡或完全水下坡差,因此危险滑动面可能向坡内发展。
这种情况必需同时验算表面滑动和深层滑动。
这种部分浸水坡的稳定分析,在工程上常将滑动面假定为两段直线组成的折线形滑动面。
折点的高程常定在水位处(图7-10a )。
采用力平衡法分析折线形滑坡体的稳定性。
力平衡法是极限平衡法的一种,其特点是静力平衡条件中只考虑土体是否移滑而不考虑是否转动。
这时作用在滑动土体上的力系只须满足主向量等于0的平衡条件即∑∑==00z x F F 和,而不考虑是否满足力矩平衡条件。
假定作用在折线滑动面上的正压力分别为N 1、N 2(图7-10b )。
根据稳定安全系数的定义,滑动面上的抗剪力可分别表示为s F tg N T 111φ=和s F tg N T 222φ=。
滑动土体上待定的未知量为N 1、N 2和安全系数F s ,而滑动土体力的平衡方程只有两个,是一个超静定的课题。
将块体从折点处竖直切开(图7-10c ),变成两个块体,这样可以建立4个力的平衡方程。
但是原来DE 面上的内力P 1在块体切开后变成外力,因而又增加了两个未知量,即P 1和P 1的方向θ,仍然是超静定问题。
为使问题可解,必须做某种假定以减少未知量的数目。
通常的做法是假定P 1的方向:或者假定P 1的方向是水平向,或者是平行于内坡DC ,或者平行于外坡BE ;还可以假定ED 也是滑裂面,此时P 1与ED 的法线成夹角φ,φ为土的内摩擦角。
今假定P 1与内坡DC 平行。
考虑块体BCDE 的平衡,有 5)-(7 )cos (1sin 111111φααtg W F W P s ∙-= 式中,W 1—块体BCDE 的重量;1φ—水位以上土的内摩擦角。
然后分析块体EDA 沿AD 面滑动的稳定性,将P 1和重力W 2分别沿AD 面分解为切向力和法向力,算出滑动力和抗滑力,从而得到安全系数的表达式为6)-(7 sin )cos(]cos )sin([22211222211αααφαααW P tg W P F s +-+-= 式中2φ为水位以下土的内摩擦角。
用迭代法解式(7-5)和式(7-6),求得的安全系数Fs 就是沿CD 和DA 面滑动的安全系数。
但是滑动面CD 和DA 是任意假定的,因此得到的安全系数不能代表整个边坡的稳定性。
还必须假定各种不同的水位以及各种折角α1、α2进行多个滑动面计算,以确定最危险的水位高程和最不利的滑动面位置,得到最小的安全系数,才是真正的边坡稳定安全系数。
第三节 粘性土坡的稳定分析粘性土的抗剪强度由摩擦强度和粘聚强度两个组成部分。
由于粘聚力的存在,粘性土坡不会像无粘性土坡一样沿坡面表面滑动。
在粘性土坡坡面上选取一薄片土体进行稳定性分析。
如果这片土体有一定的面积,但厚度是一个微量,则重量和由此而产生的滑动力也是一个微量。
在抗滑力中,摩擦力虽然是微量,而粘聚力则因为有一定的面积因此较大。
稳定安全系数等于抗滑力除以滑动力,因此稳定安全系数很大,说明不会沿边坡表面滑动。
危险的滑动面必定深入土体内部。
根据土体极限平衡理论,可以推导出均质粘性土坡的滑动面为对数螺线曲面,形状近似于圆柱面,在断面上即为圆弧面。
现场滑坡体形态的观察也证明了这一理论推断。
因此,在工程设计中常假定滑动面为圆弧面。
建立在这一假定上的稳定分析方法称为圆弧滑动法,是极限平衡法的一种常用分析方法。
一、整体圆弧滑动法设一个均质的粘性土坡(图7-13),AC 为滑动圆弧,O 为圆心,R 为半径。
假定边坡失去稳定就是滑动土体绕圆心发生转动。
把滑动土体当成一个刚体,滑动土体的重量W 将使土体绕圆心O 旋转,转动力矩为M s =Wd ,d 为过滑动土体重心的竖直线与圆心O 的水平距离。
抗滑力矩M s 由两部分组成:一是滑动面AC 上粘聚力产生的抗滑力矩,其值为c ·AC ·R ,c 为土的粘聚力;另一项是滑动土体重量在滑动面上的反力所产生的抗滑力矩。
反力的大小和方向与土的内摩擦角φ值有关。
但是因为滑动面上反力的分布无法确定,因此对于φ>0的土,此处无法求得摩擦力所产生的抗滑力矩。
而对于φ=0的土,滑动面是一个光滑面,反力的方向必定垂直于滑动面,即通过圆心O ,不产生力矩,因此抗滑力矩只有c ·AC ·R 一项。
这时稳定安全系数可用下式定义:8)-(7 WdR AC c M M F s R s ∙∙===滑动力矩抗滑力矩 公式(7-8)只适用于φ=0的土。
二、条分法的基本概念为了将圆弧滑动法应用于φ>0的粘性土,通常采用条分法。
条分法就是将滑动土体竖直分成若干土条,把土条当成刚体,分别求作用于各土条上的力对圆心的滑动力矩和抗滑力矩,然后按式(7-8)求土坡的稳定安全系数。
把滑动土体分成若干土条后,土条的两个侧面存在着条块间的作用力(图7-14)。
作用在条块i 的力,除重力W i 外,条块侧面ac 和bd 作用有法向力P i 和P i+1、切向力H i 和H i+1以及法向力的作用点离弧面的高度h i 和h i+1。
滑弧段cd 的长度为l i ,其上作用着法向力N i 和切向力T i ,T i 中包括粘聚阻力c i l i 和摩擦阻力N i tg φi (库伦定理)。