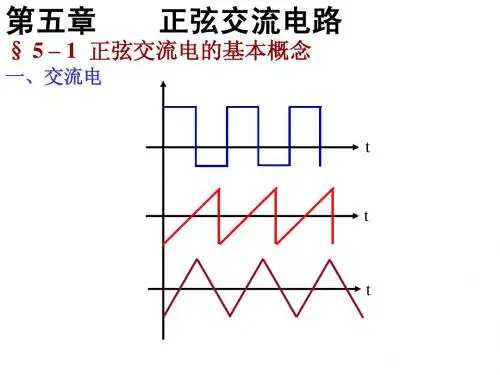
正弦交流电的基本概念
一、周期、频率与角频率
正弦交流电每重复变化一次所经历的时间称为周期，用T 表示，周期的单位为秒（s ）。
正弦交流电在单位时间内变化所完成的循环次数称为频率，用f 表示，频率的单位为赫兹（Hz ）。
例如，在一秒钟内完成三次循环，它的频率就是 3 Hz ，一次循环等于13秒。
由定义可知，频率等于周期的倒数，即1f T =或1
T f =
T 的单位为秒（S ）；
f 的单位为赫兹（Hz ）；
比较频率和周期的定义可知，二者互为倒数，显然1
Hz S =。
工业用电标准频率在不同的国家有不同
的规定。
我国和世界大多数国家规定，工业用电标准频率为50Hz 。
美国、日本和部分欧洲国家采用的工业用电标准频率为60Hz 。
周期和频率表示正弦交流电变化的快慢，周期愈长，正弦交流电变化愈慢；频率愈高，正弦交流电变化愈快。
正弦交流电变化的快慢除可用周期和频率来表示外，还可用角频率ω来表示。
所谓角频率是指正弦交流电在单位时间内变化的角度，即每秒变化的弧度数。
如每秒角度变化360°也就是一周，即为2π弧度。
如果在一秒内，旋转了四周，即转过了4×2π=8π弧度。
因为正弦量完成一个循环的变化，经历了2π弧度，所以角频率和频率之间的关系为2f ω
π=。
角频率的单位为弧度/秒
（rad/s ）。
角频率愈高，正弦交流电变化愈快。
二、幅值与有效值
正弦交流电在变化过程中出现的最大瞬时值称为正弦交流电的幅值或最大值。
用大写字母加下标m 来表示，如I m 和U m ，分别表示电流和电压的幅值。
然而，工程上一般所说的正弦交流电的大小不是指最大值，而是指有效值。
因为有效值能更确切地反映正弦交流电在电功率、电能和机械力等方面的效果。
电气设备铭牌上所标明的额定电压和额定电流都是有效值。
有效值是如何定义的呢？
我们以电流为例，如果一个周期性电流i 通过某一电阻R ，在一个周期内产生的热量与另一个直流电流I 通过电阻R 在相等时间内产生的热量相等，则将此直流电流的量值I 称为该周期性电流i 的有效值。
有效值用大写字母表示，如I 、U 、E 分别表示周期性电流、电压、电动势的有效值。
根据12Q Q =可得出下式
220T i Rdt I RT =⎰
由此公式可得交流电流的有效值为下式
I =同理也可得出以下2式：
U =
E =从以上公式可以看出，周期量的有效值等于它的瞬时值的平方在一个周期内的平均值的平方根，因此，有效值又称为方均根值。
当电流为正弦量时，其有效值与最大值的关系为I
=
同理可得正弦电压的有效值为U =
三、初相位与相位差
正弦交流电的表达式中的 (ωt+ψ)反映正弦交流电变化的进程，称为正弦交流电的相位角或相位。
当t=0时正弦交流电的相位角ψ称为初相位或初相。
初相反映正弦交流电在计时起点的状态。
初相与参考方向和计时起点的选择有关，参考方向和计时起点选择不同，正弦交流电的初相位不同，其初始值（t=0时的值）也不同。
幅值、角频率和初相位三个量能够完整的表达正弦量的特征，故将幅值、角频率和初相位称为正弦量的三要素。
已知这三个量就可以确定对应的正弦量。
例如，sin()m i i I t ωϕ=+，sin()m u u U t ωϕ=+。
在分析正弦交流电路的过程中，常常需要比较同频率的两个正弦量之间的相位关系。
例如，某一电路中电流i 和电压u 是同频率的正弦量，它们的波形如图所示。
它们的表达式分别为页面所列：i 和u 的相位之差为()()u i u i
t t ϕωψωψψψ=+-+=-
两个同频率的正弦量的相位角之差称为相位差，用ϕ表示。
可见，两个同频率的正弦量的相位差等于它们的初相位之差。
同频率的两个正弦量的相位差是一个与时间和计时起点无关的常数。
ϕ通常在ϕπ≤的范围内取值，即相位差ϕ不大于180°。
如果0u i ϕψψ=->，即ψu >ψi ，我们说，在相位上电压u 超前于电流i 的角度为ϕ，或者说，
电流i 滞后于电压u 的角度为
ϕ。
其物理意义是u 较i 先到达正的幅值（或负的幅值），u 到达正的幅值的时间要比i 到达正的幅值的时间早/t
ϕω=秒。
如果0u i ϕψψ=-<，即ψu <ψi ，这时电压u 与电流i 的相位关系刚好与上述情况相反。
那么，当0u i
ϕψψ=-=时呢？
如果，0u i ϕψψ=-=，即ψu =ψi ，则称电压u 与电流i 同相位，0ϕ=，简称同相。
如果u i
ϕψψπ=-=，则称电压u 与电流i 反相。
这时u 与i 的变化进程恰好相反，一个到达正的幅
值，而另一个到达负的幅值。
