当前位置：文档之家 › 7-5可降阶的高阶微分方程分解

7-5可降阶的高阶微分方程分解

  • 格式：ppt
  • 大小：3.48 MB
  • 文档页数：15

下载文档原格式

  / 15

合集下载

高数同济六版课件D75可降阶高阶微分方程

高数同济六版课件D75可降阶高阶微分方程
例题一
求解一阶线性微分方程$y' - 2xy = x^2e^{x^2}$，并给 出初始条件$y(0) = 1$下的特解
01
例题二
分析一阶线性微分方程$y'
+
frac{2}{x}y = x^2$的解的结构，并讨
论初始条件对解的影响
02
03
例题三
通过常数变易法求解一阶线性微分方 程$y' - y = xe^x$，并验证所得解的 正确性
物理应用
在物理学中，许多实际问题可以抽象为可降阶高阶微分方程的形式，如振动、 波动、电磁场等问题。通过求解这些方程，可以得到实际问题的解析解或近似 解。
解题方法概述
变量替换法
通过引入新的变量或函数，将原方程转化为低阶微分方程或易于求解 的形式。
积分法
利用积分公式或技巧，对方程进行逐次积分，从而降低微分方程的阶 数。
常用变量代换技巧
幂函数代换
将方程中的某一项或几项用幂函数代替，降 低方程阶数或化简方程。
三角函数代换
利用三角函数的性质进行代换，将方程转化 为三角函数方程进行求解。
指数函数与对数函数代换
根据指数函数与对数函数的性质进行代换， 简化方程形式。
通过变量代换化简复杂方程
分析方程结构，选择 合适的代换方法。
01
方程特点
方程中不显含未知数y，但可能 显含y的导数。
02
03
求解方法
示例
通过变量代换，将原方程转化为 新变量的微分方程，进而求解得 到通解。
x^2y'' + 3xy' = 0，通过变量代 换t = y'，可将其转化为一阶线 性微分方程。
显含未知数y但可化为不显含形式型微分方程

7-5可降阶高阶方程

7-5可降阶高阶方程

分离变量,得
1 P
d
P
1 x
d
x，积分得 ln
P
ln
x
ln C1
P C1 , 即 d y C1 ， x dx x
对它两端积分,得 y y C1 ln x C2 .
10
三、 y f ( y, y) 型的微分方程
特点： 不显含自变量 x.
解法： 令y dy P, 则y P d p ,
复习
1. 微分方程的概念
微分方程; 阶; 解; 通解; 特解; 定解条件.
2. 可分离变量方程 g( y)d y f ( x)dx 的求解方法:
分离变量法步骤: 1.分离变量;
2.两端积分-------隐式通解.
3.齐次方程
形如
dy dx
(
y x
)的微分方程.
解法：作变量代换u y , 即 y xu, 则 d y u x d u .
则:P 3(1 x2 ), 即y 3(1 x2 ), 两边积分得: y 3x x3 C1,
由y x0
1得：1 C1,
则所求的特解为:y 3x x3 1.
9
例3 求微分方程xy y 0的通解.
解 令y P(x), 则 y P d P , dx
代入原方程 xP P 0, 即x d P P, dx
一阶线性非齐次微分方程的通解为:
y e P(x)d x [ Q( x)e P( x)dx d x C]
Ce P( x)d x e P( x)d x Q( x)e P( x)d x d x
齐次通解
非齐次特解
即 非齐通解 = 齐通解 + 非齐特解 ——线性微分方程解的结构，是很优良的性质.
解法？

可降阶的高阶微分方程

可降阶的高阶微分方程
第七节 可降阶的高阶微分方程
一、 y(n) f ( x) 型
特点: 左端是未知函数 y 的n 阶导数, 右端是
自变量x 的一个已知函数,且不含未知函数 y 及其
导数 y.
两边积分 y(n1) f ( x)dx C1
再积分
y(n2) [ f ( x)dx C1]dx C2
……
接连积分n 次,得到含有n 个任意常数的通解.
例1 求微分方程 y e2x cos x 的通解.
解
y
(e 2 x
cos
x)dx
1 e2x 2
sin x
C1 ,
y
1 2
e2x
sin
x
C1
dx
1 4
e2x
cos
x
C1 x
C2,
通解为 y
1 4
e2x
cos
x
C1 x
C2
dx
1 8
e2x
sin
x
C1 x2
C2 x
C3 .
二、y f (x, y) 型
可得
p C1 y,
dy dx
C1
y,
即
dy y
C1dx,
原方程通解为 y C2ec1x .
F( x, p,, p(nk) ) 0
求出通解后, 再积分k次,即可求得原方程的通解.
例3 解方程 y(5) 1 y(4) 0. x
解 令 y(4) p( x), 则方程变为
p 1 p 0, 可分离变量方程 x
由分离变量法解得 p C1 x. 于是
y(4) C1 x,
所以原方程的通解为
解 设 y p,代入原方程, 得
dp 2 x dx p 1 x2

可降阶的高阶微分方程

可降阶的高阶微分方程

三、形如y″=f(y,y′)型的微分方程
【例4】
求微分方程yy″－y′2－y′=0的通解． 解方程不显含自变量x，设y′=p，则
，代入方程得
在y≠0,p≠0时，约去p并整理，得
这是关于p的一阶线性微分方程，利用公式解之得 p=C1y－1，即y′=C1y－1，再分离变量并两端积分，便得方程 的通解为
这是一阶方程，设其通解为
因y′=p(x)，于是
p=φ(x,C1)，
dydx=φ(x,C1)，
两端积分，得
y=∫φ(x,C1) dx+C2．
二、形如y″=f(x,y′)型的微分方程
【例2】
解方程xy″=y′lny′．
解设y′=p(x)，则
，方程化为
分离变量，得
为所求方程的通解．
二、形如y″=f(x,y′)型的微分方程
【例3】
三、形如y″=f(y,y′)型的微分方程
方程 y″=f(y,y′)（6-19）
中不显含自变量x．为了求出它的解，我们令y′=p，并利用复合函数 的求导法则把y″化为对y的导数，即
这样，方程（6-19）就成为
这是一个关于y,p变量的一阶微分方程．设它的通解为 y′=p=φ(y,C1)，
分离变量并积分，便得方程的通解为
可降阶的高阶 微分方程
一、形如y″=f(x)型的微分方程
对于微分方程
y″=f(x)，
其右端仅含自变量x，如分得
y′=∫f(x)dx+C1，
y=∫(∫f(x)dx)dx+C1x +C2． 以此类推，对于n阶微分方程，连续积分n次，便得含
有n个任意常数的通解．
一、形如y″=f(x)型的微分方程
【例1】

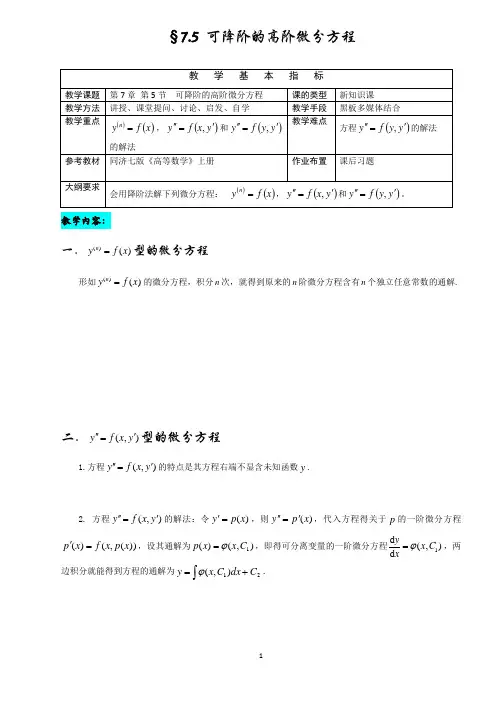
高等数学上7.5可降阶的高阶微分方程

高等数学上7.5可降阶的高阶微分方程
2
1 2、 y = − ln(ax + 1)； a
1 3、 y = ( x + 1)4. 2 1 1 y = x3 + x + 1. 三、 6 2
四、恰当导数方程
例 4
求方程 yy′′ + y′2 = 0的通解.
解 1 将方程写成 d ( yy′) = 0,
dx
故有 yy′ = C1 ,
即 ydy = C1dx,
.
五、变量代换降阶法
例 6 解
求方程 xyy′′ − xy′2 = yy′ 的通解.
∫ zdx , 设y=e
∫ zdx , y′ = z ⋅ e
∫ zdx + z ⋅ ze∫ zdx , y′′ = z′e
代入原方程, 代入原方程,得
解其通解为 z = C x,
z′x = z，
2
∫ Cxdx = C eC x . 原方程通解为 y = e 2
d2x m 2 = F（t） dt 由题设, 由题设 t = 0时，F(0) = F0 , 且力随时间的增大而均 匀地减小; 匀地减小 所以 F(t ) = F0 − kt;
又当t = T时, F(T ) = 0, 从而 t F(t ) = F0 (1 − ) T d 2 x F0 t 方程为 (1 − ) 2 = m T dt 初始条件为 x |t =0 = 0, dx |t =0 = 0 dt dx F0 t2 两端积分得 = (t − ) +C1 dt m 2T
′′ = ( y − xy′)2 的通解. 例 5 求方程 x yy
2
解
∫ zdx , 代入原方程 得 z′ + 2 z = 1 , 代入原方程,得 设y=e x x2

7-5 可降阶的高阶微分方程(高等数学)

7-5 可降阶的高阶微分方程(高等数学)

§7.5 可降阶的高阶微分方程教学内容：一．()()n y f x =型的微分方程 形如()()n y f x =的微分方程，积分n 次，就得到原来的n 阶微分方程含有n 个独立任意常数的通解.二．(,)y f x y '''=型的微分方程1.方程(,)y f x y '''=的特点是其方程右端不显含未知函数y .2. 方程(,)y f x y '''=的解法：令)(x p y ='，则)(x p y '=''，代入方程得关于p 的一阶微分方程))(,()(x p x f x p ='，设其通解为),()(1C x x p ϕ=，即得可分离变量的一阶微分方程1d (,)d =y x C x ϕ，两边积分就能得到方程的通解为⎰+=21),(C dx C x y ϕ.三．(,)y f y y '''=型的微分方程1．方程(,)y f y y '''=的特点是其方程右端不显含自变量x .2. 方程(,)y f y y '''=的解法：令d ()d y p y x=，利用复合函数的求导法则把y ''化为对y 的导数，则d d d d d d d d '''===y p y p y p x y x y,于是方程),(y y f y '=''可化为d (,)d =p p f y p y ,这是关于y 和p 的一阶微分方程，设其通解为),(1C y p ϕ=，即1d (,)d =y y C x ϕ，可求出原方程的通解21d (,)y x C y C ϕ=+⎰.四．例题讲解例1.求微分方程2e x y x '''=+的通解.例2.求微分方程x y x y +'=''1的通解.例3.求微分方程2221e 2()0y y y y y y ''''+-=满足初始条件12e |1x y =-=，12e|e x y =-'=的特解.。

7-5 可降阶的高阶微分方程-精品文档

7-5 可降阶的高阶微分方程-精品文档

解
f( 二、 y x ,y ) 型微分方程
其特点为： 二阶方程中不显含未知 函数 y.
dp 令 p y， 则 y ， 解法： dx
原方程可化为一阶方程
dy ( x ,C ) ， 如果其通解为 p 1 即有 ( x , C ) ， 1 dx 上式两端积分，可得原 方程的通解为 ：
5 3 2 y d x d x d x d x d . 1 2 3 4 5
返回
三、 y f ( y ,y ) 型微分方程
其特点为：二阶方程中不显含自变 量x. dp dp dy dp 则 y p ， 解法：令 p y， dy dx dy dx
2 2 故原方程的通解为 ： C y 1 ( C x C ) . 1 1 2
返回2 例 Fra bibliotek 求方程 y y y 0 的通解 .
d ) (y y 0 , 解 将方程改写成 dx y dy Cdx , 故有 y y C ,即
2 两边积分得通解 y C x C . 1 2
函数 y，一阶线性非齐 解 此二阶方程不显含未知 dp 次微分方程 令 y p， 则y ， dx dp p dp 2 x, x 0 , 即 原方程可化为 x p dx dx x dx dx 从而p y e x xexdx C 1 1 2 1 2 C1 xdx C 1 x x 3 x 13 y x C ln C x . 故原方程的通解为 ： 1 2 9
y ln C cos x 上式两端再积分一次得 2 1 ln 由yx 2 得 C 2 1 2 4 ln cos x . 故所求特解为 ： y

可降阶的高阶微分方程

可降阶的高阶微分方程
即 由
2 y c ( 1 x ) p c1 (1 x ) 1
2
y x0 3 得 c1 3
y 3(1 x 2 ) y x 3 3 x c2
由 y x 0 1 c2 1 故 y x 3x 1
3
例6 解方程 y 1 ( y )2 . 看成类型二的特例
再利用
得 C2 0, 故所求质点运动规律为
F0 2 t 3 x (t ) 2m 3T
二、 y f ( x , y ) 型
特点： 右端不显含未知函数 y 解法： 降阶 令ቤተ መጻሕፍቲ ባይዱ
y p y p
回代 y p 得
代入原方程得
dp f ( x , p) dx
若已求得其通解为 p ( x , c1 )
2 d P dP 2 2 y P P ( ) , , 2 dy dy
代入原方程得到新函数 P ( y )的 ( n 1)阶方程 ,
dy 求得其解为 P ( y ) ( y, C1 , , C n1 ) , dx
原方程通解为
dy x Cn ( y , C1 , , C n1 )
可降阶的高阶微分方程
前面介绍了几种标准类型的一阶方程及其求 解方法，但是能用初等解法求解的方程为数相当 有限，特别是高阶方程，除去一些特殊情况可用 降阶法求解，一般都没有初等解法， 本节介绍几种特殊的高阶方程，它们的共同 特点是经过适当的变量代换可将其化成较低阶的 方程来求解。
§4 可降阶的高阶微分方程
f ( x , z ,, z
( n k 1 )
).
求得 z ,
将 y ( k ) z 连续积分 k次, 可得通解.

常微分方程3.1 可降阶的高阶微分方程

常微分方程3.1 可降阶的高阶微分方程

参数法的基本思想 参数法的应用范围 参数法的求解步骤 参数法的优缺点
描述物理现象：可降阶的高阶微分方程可以用来描述复杂的物理现象，如振荡、波动、控制 等。
建立数学模型：通过可降阶的高阶微分方程，可以建立物理系统的数学模型，从而更好地理 解和分析物理现象。
数值模拟：可降阶的高阶微分方程可以用于数值模拟，通过计算机程序模拟物理系统的行为， 从而更好地预测和控制系统的行为。
定义和分类：介绍了可降阶的高阶微分方程的定义和分类，包括具有代表性的几种类型。
求解方法：总结了可降阶的高阶微分方程的求解方法，包括常用的数值方法和解析方法。
应用领域：列举了可降阶的高阶微分方程在各个领域的应用，如物理、化学、生物、工程等。
未来研究方向：展望了可降阶的高阶微分方程未来的研究方向，包括新的求解方法、应用领 域的拓展等。
分解法：将高阶微分方程分解为多个一阶微分方程，逐个求解，最后得到原方程的解。
降阶法：通过适当的变换，将高阶微分方程降为低阶微分方程，然后求解。 近似法：对于某些难以直接求解的高阶微分方程，可以采用近似法求解，如Runge-Kutta方法等。
数值解法：对于一些实际问题，可以采用数值解法求解高阶微分方程，如有限差分法、有限元法等。
优化设计：可降阶的高阶微分方程可以用于优化设计，通过调整系统的参数，使系统的性能 达到最优。
机械工程：可降 阶的高阶微分方 程可以用于描述 机械系统的动态 行为，例如弹簧阻尼系统、振荡 器等。
航空航天工程： 可降阶的高阶微 分方程可以用于 描述飞行器的动 态特性，例如空 气动力学、飞行 控制等。
电子工程：可降 阶的高阶微分方 程可以用于描述 电路系统的动态 行为，例如RC电 路、RLC电路等。
添加文档副标题

可降阶的高阶微分方程

可降阶的高阶微分方程
§10.3 可降阶的高阶微分方程
( n) y f ( x ) 型的微分方程 一.
二. y f ( x, y) 型的微分方程
三. y f ( y, y) 型的微分方程
教学目标
1. 掌握三种特殊高阶方程的求解方法.
机动
目录
上页
下页
返回
结束
从本节起，我们将讨论二阶及二阶以上的微分方程，即
y f ( x, y)
令 y p( x ), 则 y
dp dx
3.
y f ( y, y)
令 y p( y ),
dp 则 y p dy
16
机动 目录 上页 下页 返回 结束
2018/7/27
思考练习
1. 方程 y f ( y) 如何代换求解 ? 答: 令 y p( x ) 或 y p( y ) 均可. 一般说, 用前者方便些. 有时用后者方便 . 例如, y e
1 3 C1 ( x x ) C 2 3
以条件 y x0 1 ， y x0 3 代入得 C1 3 ， C2 1
故所求特解为 y x 3 3 x 1
19
机动 目录 上页 下页 返回 结束
则
p F ( x,C1 )
dy F ( x,C1 ) dx 这是个一阶微分方程，两端进行积分，便可得方程
(10.3.2)的通解为
y F ( x,C1 )dx C2
7
例2 求微分方程 xy y x 2 0 的通解. 解 由于方程中不显含未知函数 y ，是属于 y f ( x, y) 型. 设 y p, 则
y x 0 3 的特解.
解 令
p y 则原方程化为

常微分方程高阶方程解法

常微分方程高阶方程解法

常微分方程高阶方程解法常微分方程是描述变量关系的数学方程。

常微分方程可以分为一阶方程和高阶方程两种形式。

一阶方程是指方程中最高阶导数的阶数为一阶，高阶方程则是指方程中最高阶导数的阶数高于一阶。

高阶常微分方程解法较为复杂，需要借助一些特定的方法和技巧。

下面将介绍几种常见的高阶常微分方程解法。

1.常系数线性齐次方程的解法：齐次方程是指方程中没有出现自变量的项，且系数是常数的方程。

对于常系数线性齐次方程：a_n*y^n + a_(n-1)*y^(n-1) + ... + a_0*y = 0可以使用特征根法来求解。

假设y=e^(rx)是方程的解，代入方程可得：a_n*r^n*e^(rx) + a_(n-1)*r^(n-1)*e^(rx) + ... + a_0*e^(rx) = 0化简得到特征方程：a_n*r^n + a_(n-1)*r^(n-1) + ... + a_0 = 0解特征方程得到方程的特征根r1, r2, ..., rn，则方程的通解为：y = C1*e^(r1x) + C2*e^(r2x) + ... + Cn*e^(rnx)其中，C1, C2, ..., Cn为任意常数。

2.可降阶的高阶常微分方程的解法：可降阶的高阶常微分方程是指可以通过变量代换和符号分解等方法将高阶方程转化为一阶方程的形式。

例如，对于二阶常系数线性非齐次方程：a_2*y'' + a_1*y' + a_0*y = f(x)可以通过令z=y'代换变量，得到一阶常系数线性非齐次方程：a_2*z' + a_1*z + a_0*y = f(x)这样，高阶方程就转化为了一阶方程，可以采用一阶方程的解法来求解。

解出z后再求一次积分即可得到y的解。

3.常微分方程的级数解法：对于某些高阶常微分方程，可以采用级数展开的方法得到解的近似表达式。

假设方程的解可以表示为幂级数的形式：y = ∑(n=0 to ∞) a_n*x^n将该表达式代入方程，逐次求出各个系数a_n，即可得到解的级数表达式。

高等数学课件--D7_5可降阶高阶微分方程

高等数学课件--D7_5可降阶高阶微分方程

x 0
0, 得 C2 1
故所求特解为
2012-10-12
1 e
y
x
目录 上页 下页 返回 结束
同济版高等数学课件
例8.
二阶可导, 且
上任一点 P(x, y) 作该曲线的
切线及 x 轴的垂线, 上述两直线与 x 轴围成的三角形面 积记为 区间[ 0, x ] 上以 为曲边的曲边梯形面积 满足的方程 . 解: 在点 P(x, y) 处的切线倾角为 , 于是
2012-10-12
同济版高等数学课件
目录 上页 下页 返回 结束
例3. 求解 解:
(1 x ) y 2x y
2
y
x0
1,
y
x0
3
代入方程得
(1 x ) p 2x p
2
分离变量
积分得 ln p ln (1 x 2 ) ln C1 ,
利用 y
x0
x
2012-10-12 同济版高等数学课件
目录 上页 下页 返回 结束
内容小结
可降阶微分方程的解法 —— 降阶法
逐次积分 令 y p(x) ,
令 y p( y ) ,
同济版高等数学课件
目录 上页 下页 返回 结束
2012-10-12
思考与练习
1. 方程 如何代换求解 ?
答: 令
或
均可.
目录 上页 下页 返回 结束
dx dt

F0 m
(t
t
2
2T
) C1
利用初始条件
dx dt F0 m (t t
2
得 C1 0, 于是
)
2 3
2T
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

注意“－”号
两端积分得
l y y2 l arccos y l
利用y t0 l, 得C2 0, 因此有
m
d2 dt
y
2
k
mM y2
,
y l
R
o
由于 y = R 时
由原方程可得
因此落到地面( y = R )时的速度和所需时间分别为
t
yR
1 R
l( 2g
lR R2 l arccos
R) l
说明: 若此例改为如图所示的坐标系, 则定解问题为
第五节
第七章
可降阶高阶微分方程
一、 二、 三、
型的微分方程 型的微分方程
型的微分方程
一、 y(n) f ( x, y(k) ,, y(n1) )型
特点： 不显含未知函数y及 y,, y(k1).
解法： 令 y(k) P( x)
则 y(k1) P,
y P . (n)
(nk )
代入原方程, 得
小,直到 t = T 时 F(T) = 0 . 如果开始时质点在原点, 且
初初速度为0, 求质点的运动规律.
解: 据题意有
F0 (1 t ) mT
F0
F
F F0 (1
t T
)
对方程两边积分, 得
o Tt
dx dt
F0 m
(
t
t2 2T
)
C1
利用初始条件
得C1 0, 于是
dx F0 ( t t 2 ) dt m 2T
m
d2 dt
Hale Waihona Puke y2oy t0 0 , y t0 0
R
令 v dy，解方程可得
l
dt
y
问: 此时开方根号前应取什么符号? 说明道理 .
例.
二阶可导, 且
上任一点 P(x, y) 作该曲线的
切线及 x 轴的垂线, 上述两直线与 x 轴围成的三角形面
积记为 区间[ 0, x ] 上以 为曲边的曲边梯形面积
dy p ey dx
积分得 e y x C2 ,再由 y x0 0, 得C2 1
故所求特解为 1 e y x
例. 一个离地面很高的物体, 受地球引力的作用由 静止开始落向地面, 求它落到地面时的速度和所需时间 (不计空气阻力).
解: 如图所示选取坐标系. 则有定解问题:
y
m
d2 y dt2
y (x,C1) dx C2
例3.
例4.
(1 x2 )y 2xy
例5. 求解
y x0 1, y x0 3
解:
代入方程得
(1 x2 ) p 2x p 分离变量
积分得 ln p ln (1 x2 ) ln C1 , 利用 y x 0 3 , 得 C1 3, 于是有 y 3(1 x2 )
两边再积分得
x
F0 m
(t2 2
t3 6T
) C2
再利用
得 C2 0, 故所求质点运动规律为
x F0 ( t 2 t3 ) 2m 3T
二、 y f (x, y) 型的微分方程
设 y p (x) ,
原方程化为一阶方程
设其通解为 p (x,C1)
则得
y (x,C1)
再一次积分, 得原方程的通解
A 点受水平张力 H
y
T
M
M 点受切向张力T
H
弧段重力大小
( : 密度, s :弧长)
按静力平衡条件, 有
A g s
ox
两式相除得
故有
y
1 a
x
0
(其中a
H
g
)
1 y2 dx
y 1 a
1 y2
设 OA a, 则得定解问题:
y
1 a
1 y2
悬链线
y
M
令 y p(x), 则 y d p , 原方程化为 H a A gs
P(x)的(n-k)阶方程
P (nk) f ( x, P( x),, P (nk1) ( x)). 求得 P( x),
将 y(k) P( x) 连续积分k次, 可得通解.
例1.
解: y e2x cos x d x C1
1 2
e2x
sin
x
C1
y
1 e2x 4
cos x
C1x C2
y
1 e2x 8
sin
x
C1 x 2
C2 x
C3
例 2 求方程 xy(5) y(4) 0 的通解.
解 设 y(4) P( x), y(5) P( x)
代入原方程 xP P 0, （P 0）
解线性方程, 得 P C1 x 即 y(4) C1 x,
两端积分,得
y
1 2
C1
x
2
C2,
,
y
C1 120
x5
C2 6
x3
C3 2
x2
C4 x
C5
,
原方程通解为 y d1 x5 d2 x3 d3 x2 d4 x d5
例. 质量为 m 的质点受力F 的作用沿 ox 轴作直线
运动, 设力 F 仅是时间 t 的函数: F = F (t) . 在开始时刻
t=0时
随着时间的增大 , 此力 F 均匀地减
故方程化为
设其通解为 p ( y,C1), 即得
分离变量后积分, 得原方程的通解
例 6 求方程 yy y2 0的通解.
解 设 y p( y), 则 y p dP , dy
代入原方程得 y P dP P 2 0, 即 P( y dP P) 0,
dy
dy
由 y dP P 0， dy
k
mM y2
M : 地球质量 m : 物体质量
l R
y t0 l, y t0 0
设
v
dy dt
,
则
d2 dt
y
2
dv dt
o
代入方程得
积分得
利用v
t0
y
t0
0,
y
t 0
l,
得 C1
2kM l
v2 2kM 1 1 , y l
v dy, dt l
y dy
dt
2k M l y
两端再积分得 y x3 3 x C2 利用 y x 0 1 ,得 C2 1, 因此所求特解为
y x3 3x 1
例. 设有一均匀, 柔软的绳索, 两端固定, 绳索仅受
重力作用而下垂, 问该绳索的平衡状态是怎样的曲线 ?
解: 取坐标系如图. 考察最低点 A 到 任意点M ( x, y ) 弧段的受力情况:
dx
ox
Ar sh p ln ( p 1 p2 )
两端积分得
Ar sh
p
x a
C1,
则有
得C1 0,
两端积分得
得C2 0
故所求绳索的形状为
y
a ch
x
a (exa
x
e a
)
a2
三、y f ( y, y) 型的微分方程
令 y p , 则 y d p d p dy dx dy dx
可得 P C1 y,
dy dx
C1
y,
原方程通解为 y C2ec1x .
例7.
解初值问题
y e2y 0 y x0 0 , y
x0
1
解: 令y p ( y), 则 y p d p , 代入方程得 dy
积分得
1 2
p2
1 2
e
2
y
C1
利用初始条件,得C1 0,根据 p y0 y x0 1 0, 得