最新第三讲:双变量与多变量的描述统计分析
- 格式:ppt
- 大小:235.00 KB
- 文档页数:7

资料的统计分析——双变量及多变量分析双变量及多变量分析是指在统计分析中,同时考察两个或多个变量之间的关系。
通过对多个变量进行综合分析,可以更全面地了解变量之间的相互作用和影响。
双变量分析是指考察两个变量之间的关系,常用的方法包括相关分析和回归分析。
相关分析是用来评价两个变量之间的线性关系的强度和方向。
常用的相关系数有皮尔逊相关系数和斯皮尔曼相关系数。
皮尔逊相关系数适用于两个变量都为连续型变量的情况,而斯皮尔曼相关系数适用于至少一个变量为有序分类变量或者两个变量都为有序分类变量的情况。
回归分析是用来探究一个变量(因变量)与一个或多个变量(自变量)之间的关系的强度和方向。
常用的回归分析方法有简单线性回归分析和多元线性回归分析。
简单线性回归分析是用来研究一个自变量与一个因变量之间的线性关系的情况,而多元线性回归分析则可以同时研究多个自变量与一个因变量之间的关系。
在进行双变量分析之前,需要先进行数据的描述性分析。
描述性分析是对数据的基本特征进行总结和描述,包括样本数量、均值、方差、最小值、最大值等。
多变量分析是指同时考虑多个变量之间的关系。
常用的方法包括多元方差分析、聚类分析和因子分析。
多元方差分析是用来比较多个因素对于一个或多个因变量的影响的强度和方向。
聚类分析是用来将样本按照其中一种相似度划分为不同的群组,从而研究变量之间的内部关系。
因子分析是用来探究多个变量之间的潜在结构,从而找出变量之间的共性和差异。
除了以上方法,还可以采用交叉表分析、卡方检验和回归分析等方法来研究多个变量之间的关系。
在进行双变量及多变量分析时,需要注意以下几个问题:首先,需要选择合适的统计方法,根据变量的类型和变量之间的关系特点来选择合适的分析方法。
其次,需要注意变量之间的相关性,避免多重共线性的问题。
此外,还需要注意样本的选择和样本量的大小,以及结果的解释和推断的注意事项。
总之,双变量及多变量分析是一种重要的统计方法,可以帮助我们更全面地了解变量之间的相互作用和影响。


有用的统计学Statistics第3讲描述分析中央财经大学统计与数学学院学习目标:•单个变量时,用哪些统计表和统计图•两个变量时,用哪些统计表和统计图3.4用统计表和统计图做描述分析:双变量1.两个定性变量:(1)使用列联表–依据两个定性变量的取值交互情况,分别统计每种取值实际被观测到的频次表2六个城区不同楼层的二手房数量楼层低楼层中楼层高楼层城区东城丰台朝阳海淀石景山西城444546512129 443749413960 4965465337471.两个定性变量:(2)使用堆积柱形图–可以对比各个城区中不同楼层的二手房数量分布情况图1六个城区不同楼层二手房数量的堆积柱形图1.两个定性变量:(3)表示比例的堆积柱形图–横轴上的6根柱子高度是一致的,每根柱子内部的色块高度表示对应城区中不同楼层二手房所占的比例图2六个城区不同楼层二手房比例的堆积柱形图2.两个定量变量:使用散点图–将定量变量的观测值绘制在二维平面上–判断定量变量之间的相关关系:✓相关方向:正相关、负相关;✓相关形态:线性相关、非线形相关;✓相关关系的密切程度:强相关,弱相关,基本不相关图3面积与房价的散点图3.一个定量变量+一个定性变量:使用分组箱线图图4不同城区房价的分组箱线图–对定性变量的每个取值,单独绘制对应的定量变量数据的箱线图,把所有的箱线图放在一起做横向比较。
–如图4所示,可以在一个图内同时观察到:不同城区的房价在集中趋势、离散程度上是否有差异,不同城区是否都存在极端房价的情况小结描述两个变量时,按照它们的组合情况来选择恰当的统计表和统计图:•对于两个定性变量,可以绘制列联表、堆积柱形图来展示两个变量的观测值分布情况•对于两个定量变量,可以绘制散点图,帮助判断两个变量的相关方向、相关形态、相关关系的紧密程度。
•对于一个定性变量、一个定量变量的情况,可以绘制分组箱线图本章总结•描述统计可以帮助我们快速地从数据中提取有用信息。



两个以上类别变量关系的描述统计方法描述统计方法是研究类别变量间关系的一种方法。
类别变量是指数据被分为几个离散的组别,例如性别、种族、教育程度等。
这些变量在统计分析中经常被用来说明人口特征、社会因素等,因此描述统计方法对于社会科学研究非常重要。
1. 列联表和卡方检验列联表是一种显示两个或多个类别变量之间关系的表格。
每个变量都对应一个行或列,称为行变量或列变量。
表格中的每个单元格显示了两个变量之间的交叉频数或比例。
通过观察单元格中的数字,可以发现两个类别变量之间的关系。
例如,假设有一个调查,调查对象是所有正在购买手机的消费者。
其中,一项问题是:您购买手机时最看重哪个因素?调查者提供了四个选项:“价格”、“品牌”、“功能”和“外观”。
调查者还记录了消费者的性别和年龄段。
通过列联表可以发现,男性和女性在购买手机时最看重的因素有什么差异,年龄段也可能影响选择的因素。
卡方检验是一种用于检验列联表中变量之间是否存在显著关系的方法。
它基于卡方检验统计量,该统计量表示观察到的频数和期望频数之间的差异程度。
期望频数是基于每个变量的边际总体比例来预期的单元格频数。
在上面的例子中,卡方检验可以用来检验性别和购买因素之间是否存在关系。
如果检验结果显示具有显著关系,则可以得出结论,即性别可能影响购买因素的选择。
2. 分组统计分组统计是一种将一个或多个类别变量分成几个类别,并对它们进行数量和比例等描述的方法。
分组统计的目的是把数据分类,以便更好地理解变量之间的关系。
它通常以频数或百分比形式呈现。
例如,假设一个研究人员想要了解每个地区的性别和教育程度的分布情况。
他可能将教育程度分为“初中以下”、“高中”、“本科”、“硕士”和“博士”等五个类别,并且将性别分为“男性”和“女性”两个类别。
通过计算每个组别的频数或百分比,可以得到每个地区的性别和教育程度的分布情况。
分组统计也可以用来比较不同组别之间的差异。
例如,研究人员可以通过对不同地区的性别和教育程度进行分组统计,比较它们之间的教育水平和性别比例是否存在差异。

第三章双变量简单描述统计第一节统计相关性一、相关的概念一个变化,另一个值按照某种规律在一定范围内变化,被称为不确定的统计关系或相关关系。
例如收入与支出的关系。
注意区分函数关系与相关关系:函数关系是确定的,一个变量取某一值,另一个变量有确定的值与之对应。
例如,销售量与销售额(价格固定)。
相关关系与因果关系:相关的两个变量,不一定有因果关系。
对称关系与不对称关系:相关的两个变量有时互相影响或共同变化的,不存在某一变量变化引起另一个变化,称为对称关系。
如果X变量引起Y变量变化,而Y变量变化不引起X变量变化,则为不对称关系。
二、相关方向(direction of association)1、正相关:一个变量值增大,另一个也增大,反之都减小。
2、负相关:一个变量值增大,另一个减小。
相关方向分析只限于定序或定距变量,定类变量无高低之分,不可能有正负之分。
三、相关程度(degree of association)两个变量的相关程度有强弱之分,通常由0到1,0代表不相关,1代表全相关。
数值越大,相关关系越强。
第二节交互分类与联列表一、联列表的基本概念在讨论两个变量尤其是两个定类变量x和y是否存在相关关系时,可以先将数据按x分类,然后分别统计当x取不同类别值时y的分类情况。
就得到了数据按两个定类变量进行交叉分类的频次分布表,即二维联列表。
例1:某小区对居民的收视爱好进行调查,根据不同年龄和喜爱的电视节目类型进行分类表1:年龄和收视爱好的交叉分类表条件次数:当某一变量取不同类别值时,另一变量的频次。
频次联列表的缺陷:由于边缘次数不同,仅根据条件次数无法进行比较核分析相关关系,需要制作条件百分表,表2。
表2:不同年龄人群的收视爱好分布通过计算条件百分比,可以知道:年龄和收视爱好相关,随着年轻化,喜爱戏曲的比例逐渐下降,而歌舞和球赛越来越受欢迎。
二、制作联列表1、制表规则(1)要有表号、标题。
(2)线条简洁、符号标注在标题后或第一行变量类别后。


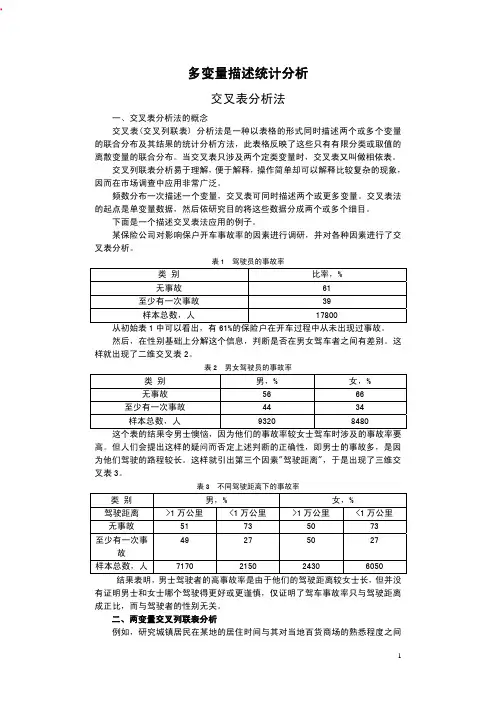
多变量描述统计分析交叉表分析法一、交叉表分析法的概念交叉表(交叉列联表) 分析法是一种以表格的形式同时描述两个或多个变量的联合分布及其结果的统计分析方法,此表格反映了这些只有有限分类或取值的离散变量的联合分布。
当交叉表只涉及两个定类变量时,交叉表又叫做相依表。
交叉列联表分析易于理解,便于解释,操作简单却可以解释比较复杂的现象,因而在市场调查中应用非常广泛。
频数分布一次描述一个变量,交叉表可同时描述两个或更多变量。
交叉表法的起点是单变量数据,然后依研究目的将这些数据分成两个或多个细目。
下面是一个描述交叉表法应用的例子。
某保险公司对影响保户开车事故率的因素进行调研,并对各种因素进行了交叉表分析。
表1 驾驶员的事故率类 别 比率,%无事故 61至少有一次事故 39样本总数,人 17800从初始表1中可以看出,有61%的保险户在开车过程中从未出现过事故。
然后,在性别基础上分解这个信息,判断是否在男女驾车者之间有差别。
这样就出现了二维交叉表2。
表2 男女驾驶员的事故率类 别 男,% 女,%无事故 56 66 至少有一次事故 44 34样本总数,人 9320 8480这个表的结果令男士懊恼,因为他们的事故率较女士驾车时涉及的事故率要高。
但人们会提出这样的疑问而否定上述判断的正确性,即男士的事故多,是因为他们驾驶的路程较长。
这样就引出第三个因素"驾驶距离",于是出现了三维交叉表3。
表3 不同驾驶距离下的事故率类 别 男,% 女,%驾驶距离 >1万公里 <1万公里 >1万公里 <1万公里 无事故 51 73 50 7349 27 50 27至少有一次事故样本总数,人7170 2150 2430 6050结果表明,男士驾驶者的高事故率是由于他们的驾驶距离较女士长,但并没有证明男士和女士哪个驾驶得更好或更谨慎,仅证明了驾车事故率只与驾驶距离成正比,而与驾驶者的性别无关。
二、两变量交叉列联表分析例如,研究城镇居民在某地的居住时间与其对当地百货商场的熟悉程度之间的关系,对“居住时间”和“熟悉程度”这两个变量进行交叉列联分析。
双变量及多变量数据的描述性统计分析双变量及多变量数据的描述性统计分析是对数据集中两个或多个变量之间的关系进行描述的过程。
这种分析通常涉及更复杂的统计技术,以便揭示变量之间的关联、趋势和模式。
以下是双变量及多变量数据描述性统计分析的主要内容和方法:双变量数据分析1. 散点图:散点图是一种用于展示两个变量之间关系的图形。
通过绘制每个观测值的点,可以直观地观察变量之间是否存在线性或其他类型的关系。
2. 相关系数:相关系数(如皮尔逊相关系数)用于量化两个变量之间的线性关系强度和方向。
它的取值范围在-1到1之间,其中1表示完全正相关,-1表示完全负相关,0表示无线性关系。
3. 协方差:协方差是另一个用于量化两个变量之间线性关系的指标。
与相关系数类似,但它是以原始数据的单位进行度量的。
4. 回归分析:回归分析是一种统计方法,用于探索两个或多个变量之间的定量关系。
通过拟合一个数学模型(如线性回归模型),可以预测一个变量基于另一个变量的值。
多变量数据分析1. 相关矩阵:相关矩阵是一个表格,显示了数据集中所有变量之间的相关系数。
这有助于识别变量之间的潜在关联和共线性。
2. 主成分分析(PCA):PCA是一种降维技术,用于减少数据集中的变量数量。
它通过创建新的、不相关的变量(主成分)来总结原始变量的信息。
3. 因子分析:因子分析是一种统计方法,用于识别数据集中的潜在结构或因子。
它类似于PCA,但更侧重于解释性,旨在揭示变量之间的潜在共同因素。
4. 聚类分析:聚类分析是一种探索性数据分析技术,用于将观测值分组成具有相似性的簇。
它可以帮助发现数据集中的自然分组或类别。
在进行双变量及多变量数据的描述性统计分析时,需要注意以下几点:确保数据的准确性和完整性,避免异常值和缺失值对分析结果的影响。
选择合适的统计方法和模型,根据数据的性质和分析目的进行决策。
注意对统计结果进行解释和说明,以便更好地理解和应用分析结果。
总的来说,双变量及多变量数据的描述性统计分析可以帮助我们更深入地理解数据集中变量之间的关系和模式,为后续的数据分析和决策提供支持。