第四章一元一次方程复习精品课件
- 格式:ppt
- 大小:61.50 KB
- 文档页数:7

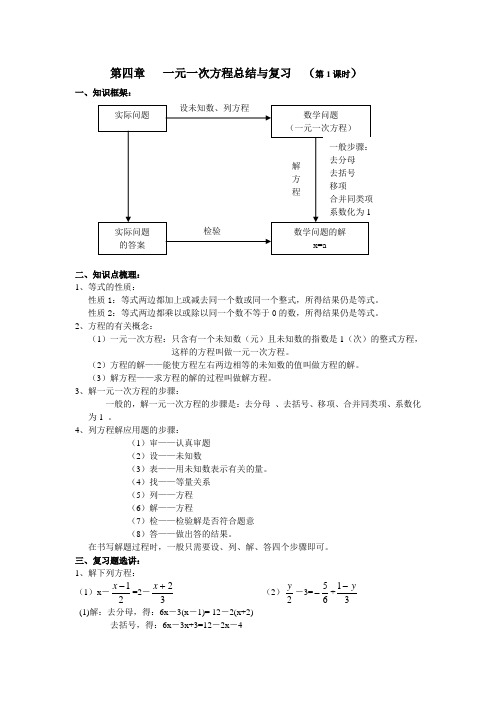
第四章 一元一次方程总结与复习 (第1课时)二、知识点梳理:1、等式的性质:性质1:等式两边都加上或减去同一个数或同一个整式,所得结果仍是等式。
性质2:等式两边都乘以或除以同一个数不等于0的数,所得结果仍是等式。
2、方程的有关概念:(1)一元一次方程:只含有一个未知数(元)且未知数的指数是1(次)的整式方程,这样的方程叫做一元一次方程。
(2)方程的解——能使方程左右两边相等的未知数的值叫做方程的解。
(3)解方程——求方程的解的过程叫做解方程。
3、解一元一次方程的步骤:一般的,解一元一次方程的步骤是:去分母 、去括号、移项、合并同类项、系数化为1 。
4、列方程解应用题的步骤:(1)审——认真审题(2)设——未知数(3)表——用未知数表示有关的量。
(4)找——等量关系(5)列——方程(6)解——方程(7)检——检验解是否符合题意(8)答——做出答的结果。
在书写解题过程时,一般只需要设、列、解、答四个步骤即可。
三、复习题选讲:1、解下列方程:(1)x -21-x =2-32+x (2)2y -3=65-+31y - (1)解:去分母,得:6x -3(x -1)= 12-2(x+2)去括号,得:6x -3x+3=12-2x -4移项,得: 6x -3x+2x=12-4-3合并同类项,得:5x=5系数化为1,得:x=1(2)解:去分母,得: 3y -18=-5+2(1-y)去括号,得: 3y -18=-5+2-2y移项,得: 3y+2y=-5+2+18合并同类项,得:5y=15系数化为1,得:y=32、如果x=-2是方程a(x+3) =21a+x 的解,求a 2-21a+1的值。
解:∵x=-2是方程a(x+3) = 21a+x 的解 则:a ×(-2+3) = 21a+(-2) ∴ a = -4∴a 2-21a+1=(-4) 2-21×(-4)+1=19 3、一根弹簧长40cm ,一端固定,另一端颗挂重物,通常所挂物体质量每增加1kg ,弹簧伸长2cm ,求弹簧长度为45cm 时所挂物体的质量。



