第三章-2(5次)-1
- 格式:ppt
- 大小:1.33 MB
- 文档页数:15

利息理论第三章课后答案《金融数学》课后习题参考答案第三章 收益率1、某现金流为:元,元,元,元,求该现金流的收益率。
解:由题意得:2、某投资者第一年末投资7000元,第二年末投资1000元,而在第一、三年末分别收回4000元和5500元,计算利率为0.09及0.1时的现金流现值,并计算该现金流的内部收益率。
解:由题意得:当时, 当时,令3、某项贷款1000元,每年计息4次的年名义利率为12%,若第一年后还款400元,第5年后还款800元,余下部分在第7年后还清,计算最后一次还款额。
解:由题意得:4、甲获得100000元保险金,若他用这笔保险金购买10年期期末付年金,每年可得15380元,若购买20年期期末付年金,则每年可得10720元,这两种年金基于相同的利率,计算。
3000o o =11000o =12000I =24000I =2001122()()()0O I O I v O I v -+-+-=23000100040000v v --=4133v i ⇒=⇒=23(0)[(47) 5.5]1000V v v v =--+⨯0.09i =(0)75.05V =0.1i =(0)57.85V =-(0)00.8350.198V v i =⇒=⇒=40.121(10.88854i v +=+⇒=571000400800657.86v pv p =++⇒=i i解:由题意得: 5、某投资基金按积累,,在时刻0基金中有10万元,在时刻1基金中有11万元,一年中只有2次现金流,第一次在时刻0.25时投入15000元,第二次在时刻0.75时收回2万元,计算k 。
解:由题意得:6、某投资业务中,直接投资的利率为8%,投资所得利息的再投资利率为4%,某人为在第10年末获得本息和1万元,采取每年末投资相等的一笔款项,共10年,求证每年投资的款项为:。
证明:7.某投资人每年初在银行存款1000元,共5年,存款利率为5%,存款所得利息的再投资利率为4%,证明:V (11)=1250(。
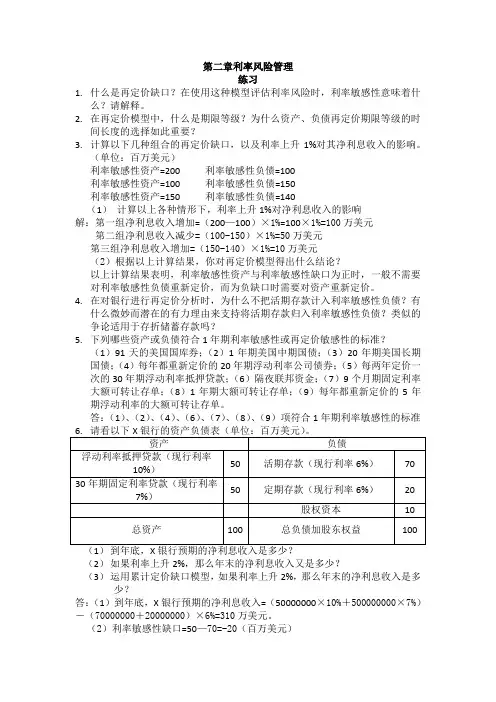
第二章利率风险管理练习1.什么是再定价缺口?在使用这种模型评估利率风险时,利率敏感性意味着什么?请解释。
2.在再定价模型中,什么是期限等级?为什么资产、负债再定价期限等级的时间长度的选择如此重要?3.计算以下几种组合的再定价缺口,以及利率上升1%对其净利息收入的影响。
(单位:百万美元)利率敏感性资产=200 利率敏感性负债=100利率敏感性资产=100 利率敏感性负债=150利率敏感性资产=150 利率敏感性负债=140(1)计算以上各种情形下,利率上升1%对净利息收入的影响解:第一组净利息收入增加=(200—100)×1%=100×1%=100万美元第二组净利息收入减少=(100-150)×1%=50万美元第三组净利息收入增加=(150-140)×1%=10万美元(2)根据以上计算结果,你对再定价模型得出什么结论?以上计算结果表明,利率敏感性资产与利率敏感性缺口为正时,一般不需要对利率敏感性负债重新定价,而为负缺口时需要对资产重新定价。
4.在对银行进行再定价分析时,为什么不把活期存款计入利率敏感性负债?有什么微妙而潜在的有力理由来支持将活期存款归入利率敏感性负债?类似的争论适用于存折储蓄存款吗?5.下列哪些资产或负债符合1年期利率敏感性或再定价敏感性的标准?(1)91天的美国国库券;(2)1年期美国中期国债;(3)20年期美国长期国债;(4)每年都重新定价的20年期浮动利率公司债券;(5)每两年定价一次的30年期浮动利率抵押贷款;(6)隔夜联邦资金;(7)9个月期固定利率大额可转让存单;(8)1年期大额可转让存单;(9)每年都重新定价的5年期浮动利率的大额可转让存单。
答:(1)、(2)、(4)、(6)、(7)、(8)、(9)项符合1年期利率敏感性的标准(2)如果利率上升2%,那么年末的净利息收入又是多少?(3)运用累计定价缺口模型,如果利率上升2%,那么年末的净利息收入是多少?答:(1)到年底,X银行预期的净利息收入=(50000000×10%+500000000×7%)-(70000000+20000000)×6%=310万美元。

第三章救生筏救生筏是在船舶遇险时船员使用的一种救生设备。
它能迅速地被施放到水面上并漂浮于水面之上供船员们登乘。
各种救生筏均具有一定的浮力,有遮风、防雨、御寒的顶篷和供求生人员食用的口粮和淡水以及必要的属具备品。
其特点是体积小、重量轻、操作简单方便。
其缺点主要表现在:无自航能力、只能在水中漂浮待救、投放后在水面易呈翻覆状态需人工扶正、浮胎易发生破损漏水等。
第一节救生筏种类、结构与一般要求一、救生筏的种类救生筏根据其结构形式,可分为刚性救生筏和气胀式救生筏两种。
(一)刚性救生筏刚性救生筏的浮力应由认可的自然浮力材料提供。
这些浮力材料应置于靠近救生筏的周边。
其浮力材料是阻燃的或用阻燃材料覆盖物加以保护筏底能防止海水进入并有效地支承乘员离开水面且御寒。
救生筏在倾覆时能自行或由一个人扶正。
刚性救生筏的结构如图3-1所示:(二)气胀救生筏它是用橡胶、尼龙布等材料制成,用气体充胀成圆形或椭圆形带有顶篷的小筏。
按施放方法不同一般分为抛投式和机械吊放式1、抛投式救生筏当船舶遇险时,筏可由人力或借助其本身重力作用抛入海中,在极短的时间内依靠充力绳拉动充气瓶阀门使其充气成形。
2、机械吊放式主要供客船或科学考查船、教学船使用。
先将筏从储藏舱室或甲板存放处取出悬挂在救生筏吊架上,拉动充气拉绳,使其在舷边充气成形。
然后系妥胶布做的登乘平台,使船员和旅客从甲板上登乘救生筏,再将筏吊落至水面。
这样,使乘员避免了爬绳梯、跳水等困难。
气胀式救生筏的结构如图3-2所示。
主要有筏体(指上下浮胎)、篷柱、篷帐、筏底四个主要部分以及一些附属设备组成。
气胀式救生筏充气成形后的外形如图3-3所示。
二、气胀式救生筏的结构1、上、下浮台:是互相独立的两个气室,在上浮胎内有两个单向筏通向篷柱,上浮胎损坏时,篷柱仍能保持支撑状态。
2、蓬柱:与上浮胎连接用于支撑篷帐的园柱形气室。
3、篷帐:是用双层锦编防水胶布制成,粘贴在篷柱上,防浪、避风、遮雨、防晒等作用。


3-1 设系统的微分方程式如下:(1) )(2)(2.0t r t c= (2) )()()(24.0)(04.0t r t c t c t c=++ 试求系统闭环传递函数Φ(s),以及系统的单位脉冲响应g(t)和单位阶跃响应c(t)。
已知全部初始条件为零。
解:(1) 因为)(2)(2.0s R s sC =闭环传递函数ss R s C s 10)()()(==Φ 单位脉冲响应:s s C /10)(= 010)(≥=t t g单位阶跃响应c(t) 2/10)(s s C = 010)(≥=t t t c(2))()()124.004.0(2s R s C s s =++ 124.004.0)()(2++=s s s R s C `闭环传递函数124.004.01)()()(2++==s s s R s C s φ单位脉冲响应:124.004.01)(2++=s s s C t e t g t 4sin 325)(3-= 单位阶跃响应h(t) 16)3(61]16)3[(25)(22+++-=++=s s s s s s C t e t e t c t t 4sin 434cos 1)(33----=3-2 温度计的传递函数为11+Ts ,用其测量容器内的水温,1min 才能显示出该温度的98%的数值。
若加热容器使水温按10ºC/min 的速度匀速上升,问温度计的稳态指示误差有多大解法一 依题意,温度计闭环传递函数11)(+=ΦTs s 由一阶系统阶跃响应特性可知:o o T c 98)4(=,因此有 min 14=T ,得出 min 25.0=T 。
视温度计为单位反馈系统,则开环传递函数为Tss s s G 1)(1)()(=Φ-Φ=⎩⎨⎧==11v TK !用静态误差系数法,当t t r ⋅=10)( 时,C T Ke ss ︒===5.21010。
解法二 依题意,系统误差定义为 )()()(t c t r t e -=,应有 1111)()(1)()()(+=+-=-==ΦTs TsTs s R s C s R s E s e C T sTs Ts ss R s s e s e s ss ︒==⋅+=Φ=→→5.210101lim )()(lim 203-3 已知二阶系统的单位阶跃响应为)1.536.1sin(5.1210)(2.1o tt et c +-=-试求系统的超调量σ%、峰值时间tp 和调节时间ts 。




《金融数学》课后习题参考答案第三章 收益率1、某现金流为:元,元,元,元,求该现金流的收益率。
解:由题意得:2、某投资者第一年末投资7000元,第二年末投资1000元,而在第一、三年末分别收回4000元和5500元,计算利率为及时的现金流现值,并计算该现金流的内部收益率。
解:由题意得:当时,当时,令3、某项贷款1000元,每年计息4次的年名义利率为12%,若第一年后还款400元,第5年后还款800元,余下部分在第7年后还清,计算最后一次还款额。
解:由题意得:4、甲获得100000元保险金,若他用这笔保险金购买10年期期末付年金,每年可得15380元,若购买20年期期末付年金,则每年可得10720元,这两种年金基于相同的利率,计算。
解:由题意得: 08688.010720153802010=⇒=i a a i i5、某投资基金按积累,,在时刻0基金中有10万元,在时刻1基金中有11万元,一年中只有2次现金流,第一次在时刻时投入15000元,第二次在时刻时收回2万元,计算k。
解:由题意得:6、某投资业务中,直接投资的利率为8%,投资所得利息的再投资利率为4%,某人为在第10年末获得本息和1万元,采取每年末投资相等的一笔款项,共10年,求证每年投资的款项为:。
证明:7.某投资人每年初在银行存款1000元,共5年,存款利率为5%,存款所得利息的再投资利率为4%,证明:V(11)=1250(。
V(11)=1000[5(1++(Is)8.甲年初投资2000元,年利率为 17%,每年末收回利息,各年收回的利息按某一利率又投资出去,至第10 年末,共得投资本息和元。
乙每年末投资150元,年利率14%,共20年,每年收回的利息按甲的再投资利率投资。
计算乙在第20年末的投资本息和。
9.某投资基金年初有投资2万元,年收益率为12%,3月末又投入资金5000元,9月末赎回资金8000元,假设1-t it=(1-t)i 计算年末基金的资金量。


3.1题(宗传玉)某甲参加一种会议,会上有6位朋友,某甲和其中每人在会上各相遇12次,每二人各相遇6次,每三人各相遇3次,每五人各相遇2次,每六人各相遇一次,1人也没有遇见的有5次,问某甲共参加了几次会议解:设A i为甲与第i个朋友相遇的会议集,i=1,…,6.则故甲参加的会议数为:28+5=33.3.2题(宗传玉)求从1到500的整数中被3和5整除但不被7整除的数的个数.解:设A3:被3整除的数的集合A5:被5整除的数的集合A7:被7整除的数的集合所以3.3.题(宗传玉)n个代表参加会议,试证其中至少有2人各自的朋友数相等。
解:每个人的朋友数只能取0,1,…,n-1.但若有人的朋友数为0,即此人和其他人都不认识,则其他人的最大取数不超过n-2.故这n个人的朋友数的实际取数只有n-1种可能.,所以至少有2人的朋友数相等.3.4题(宗传玉)试给出下列等式的组合意义.解:(a) 从n 个元素中取k 个元素的组合,总含有指定的m 个元素的组合数为)()(kn mn m k m n --=--。
设这m 个元素为a 1,a 2,…,a m ,Ai 为不含a i 的组合(子集),i=1,…,m.()∑∑∑==∈⊄==⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛-=-+⎪⎪⎭⎫ ⎝⎛==⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫⎝⎛-=ml l m l l m i i lj i lk l n k m A k n k n m n k l n l j 01),(),...,(1m1i i i i i 1)1(A A A A 111213.5题(宗传玉)设有三个7位的二进制数:a1a2a3a4a5a6a7,b1b2b3b4b5b6b7,c1c2c3c4c5c6c7.试证存在整数i 和j,1≤i≤j≤7,使得下列之一必定成立:a i=a j=b i=b j,a i=a j=c i=c j,b i=b j=c i=c j.证:显然,每列中必有两数字相同,共有种模式,有0或1两种选择.故共有·2种选择.·2=6.现有7列,.即必有2列在相同的两行选择相同的数字,即有一矩形,四角的数字相等.3.6题(宗传玉)在边长为1的正方形内任取5个点试证其中至少有两点,其间距离小于证:把1×1正方形分成四个(1/2)×.则这5点中必有两点落在同一个小正方形内.而小正方形内的任两点的距离都小于.3.7题(王星)在边长为1的等边三角形内任取5个点试证其中至少有两点,期间距离小于1/2.证:把边长为1的三角形分成四个边长为1/2的三角形,如上图:则这5点中必有两点落在同一个小三角形中.小三角形中任意两点间的距离都小于1/2.3.8题(王星)任取11个整数,求证其中至少有两个数它们的差是10的倍数。
高中数学目录必修一第一章1.1 会合与会合的表示方法1.1.1 会合的观点1.1.2 会合的表示方法第二章2.1 函数2.1.1 函数2.1.2 函数的表示方法2.1.3 函数的单一性2.1.4 函数的奇偶性2.1.5 用计算机作函数图像(选学)2.2 一次函数和二次函数2.2.1 一次函数的性质与图像2.2.2 二次函数的性质与图像2.3 函数的应用( 1)2.4 函数与方程2.4.1 函数的零点2.4.2 求函数零点近似解的一种计算方法----二分法第三章基本初等函数(1)3.1 指数与指数函数3.1.1 实数指数幂及其运算3.1.2 指数函数3.2 对数与对数函数3.2.1 对数及其运算3.2.2 对数函数3.2.3 指数函数与对数函数的关系3.3 幂函数3.4 函数的应用( 2)必修二第一章立体几何初步1.1 空间几何体1.1.1 组成空间几何体的基本元素1.1.2 棱柱棱锥棱台的构造特点1.1.3 圆柱圆锥圆台和球1.1.4 投影与直观图1.1.5 三视图1.1.6 棱柱棱锥棱台和球的表面积1.1.7 柱锥台和球的体积1.2 点线面之间的地点关系1.2.1 平面的基天性质与推论1.2.2 空间中的平行关系1.2.3 空间中的垂直关系第二章平面分析几何初步2.1 平面直角坐标系中的基本公式2.1.1 数轴上的基本公式2.1.2 平面直角坐标系中的基本公式2.2 直线的方程2.2.1 直线方程的观点与直线的斜率2.2.2 直线方程的集中形式2.2.3 两条直线的地点关系2.2.4 点到直线的距离2.3 圆的方程2.3.1 圆的标准方程2.3.2 圆的一般方程2.3.3 直线与圆的地点关系2.3.4 圆与圆的地点关系2.4 空间直角坐标系2.4.1 空间直角坐标系2.4.2 空间两点距离公式必修三第一章算法初步1.1 算法与程序框图1.1.1 算法的观点1.1.2 程序框图1.1.3 算法的三种基本逻辑构造和框图表示1.2 基本算法语句1.2.1 赋值输入输出语句1.2.2 条件语句1.2.3 循环语句1.3 中国古代数学中的算法事例第二章统计2.1 随机抽样2.1.1 简单的随机抽样2.1.2 系统抽样2.1.3 分层抽样2.1.4 数据的采集2.2 用样本预计整体2.2.1 用样本的频次散布预计整体的散布2.2.2 用样本的数字特点预计整体的数字特点2.3 变量的有关性2.3.1 变量间的互相关系2.3.2 两个变量的线性有关第三章概率3.1 事件与概率3.1.1 随机现象3.1.2 事件与基本领件空间3.1.3 频次与概率3.1.4 概率的加法公式3.2 古典概型3.2.1 古典概型3.2.2 概率的一般加法公式(选学)3.3 随机数的含义与应用3.3.1 几何概型3.3.2 随机数的含义与应用3.4 概率的应用必修四第一章基本的初等函数(2)1.1 随意角的观点与弧度制1.1.1 角的观点的推行1.1.2 弧度制和弧度制与角度制的换算1.2 随意角的三角函数1.2.1 三角函数的定义1.2.2 单位圆与三角函数线1.2.3 同角三角函数的基本关系式1.2.4 引诱公式1.3 三角函数的图像与性质1.3.1 正弦函数的图像与性质1.3.2 余弦函数正切函数的图像与性质1.3.3 已知三角函数值求角第二章平面向量2.1 向量的线性运算2.1.1 向量的观点2.1.2 向量的加法2.1.3 向量的减法2.1.4 数乘向量2.1.5 向量共线的条件和轴上向量坐标运算2.2 向量的分解和向量的坐标运算2.2.1 平面向量基本定理2.2.2 向量的正交分解与向量的直角坐标运算2.2.3 用平面向量坐标表示向量共线条件2.3 平面向量的数目积2.3.1 向量数目积的物理背景与定义2.3.2 向量数目积的运算律2.3.3 向量数目积的坐标运算与胸怀公式2.4 向量的应用2.4.1 向量在几何中的应用2.4.2 向量在物理中的应用第三章三角恒等变换3.1 和角公式3.1.1 两角和与差的余弦3.1.2 两角和与差的正弦3.1.3 两角和与差的正切3.2 倍角公式和半角公式3.2.1 倍角公式3.2.2 半角的正弦余弦和正切3.3 三角函数的积化和差与和差化积必修五第一章解三角形1.1 正弦定理和余弦定理1.1.1 正弦定理1.1.2 余弦定理1.2 应用举例第二章数列2.1 数列2.1.1 数列2.1.2 数列的递推公式(选学)2.2 等差数列2.2.1 等差数列2.2.2 等差数列的前n 项和2.3 等比数列2.3.1 等比数列2.3.2 等比数列的前n 项和第三章不等式3.1 不等关系与不等式3.1.1 不等关系与不等式3.1.2 不等式性质3.2 均值不等式3.3 一元二次不等式及其解法3.4 不等式的实质应用3.5 二元一次不等式(组)与简单的线性规划问题3.5.1 二元一次不等式(组)所表示的平面地区3.5.2 简单线性规划选修 2-1第一章常用逻辑用语1.1 命题与量词1.1.1 命题1.1.2 量词1.2 基本逻辑联络词1.2.1 且与或1.2.2 非(否认)1.3 充足条件必需条件与命题的四种形式1.3.1 推出与充足条件必需条件1.3.2 命题的四种形式第二章圆锥曲线方程2.1 曲线方程2.1.1 曲线与方程的观点2.1.2 由曲线求它的方程由方程研究曲线性质2.2 椭圆2.2.1 椭圆的标准方程2.2.2 椭圆的几何性质2.3 双曲线2.3.1 双曲线的标准方程2.3.2 双曲线的几何性质2.4 抛物线2.4.1 抛物线的标准方程2.4.2 抛物线的几何性质2.5 直线与圆锥曲线第三章空间向量与几何体3.1 空间向量及其运算3.1.1 空间向量的线性运算3.1.2 空间向量的基本定理3.1.3 两个向量的数目积3.1.4 空间向量的直角坐标运算3.2 空间向量在立体几何中的应用3.2.1 直线的方向向量与直线的向量方程3.2.2 平面的法向量与平面的向量表示3.2.3 直线与平面的夹角3.2.4 二面角及其胸怀3.2.5 距离(选学)选修 2-2第一章导数及其应用1.1 导数1.1.1 函数的均匀变化率1.1.2 刹时速度与导数1.1.3 导数的几何1.2 导数的运算1.2.1 常数函数与幂函数的导数1.2.2 导数公式表及数学软件的应用1.2.3 导数的四则运算法例1.3 导数的应用1.3.1 利用导数判断函数的单一性1.3.2 利用导数研究函数的极值1.3.3 导数的实质应用1.4 定积分与微积分的基本定理1.4.1 曲边梯形面积与定积分1.4.2 微积分基本定理第二章推理与证明2.1 合情推理与演绎推理2.1.1 合情推理2.1.2 演绎推理2.2 直接证明与间接证明2.2.1 综合法与剖析法2.2.2 反证法2.3 数学概括法2.3.1 数学概括法2.3.2 数学概括法应用举例第三章数系的扩大与复数3.1 数系的扩大与复数的观点3.1.1 实数系3.1.2 复数的观点3.1.3 复数的几何意义3.2 复数的运算3.2.1 复数的加法与减法3.2.2 复数的乘法3.2.3 复数的除法选修 2-3第一章计数原理1.1 基本计数原理1.2 摆列与组合1.2.1 摆列1.2.2 组合1.3 二项式定理1.3.1 二项式定理1.3.2 杨辉三角第二章概率2.1 失散型随机变量及其散布列2.1.1 失散型随机变量2.1.2 失散型随机变量的散布列2.1.3 超几何散布2.2 条件概率与实践的独立性2.2.1 条件概率2.2.2 事件的独立性2.2.3 独立重复试验与二项散布2.3 随机变量的数字特点2.3.1 失散型随机变量的数学希望2.3.2 失散型随机变量的方差2.4 正态散布第三章统计事例3.1 独立性查验3.2 回归剖析选修 4-4第一章坐标系1.1 直角坐标系平面上的伸缩变换1.1.1 直角坐标系1.1.2 平面上的伸缩变换1.2 极坐标系1.2.1 平面上点的极坐标1.2.2 极坐标与直角坐标的关系1.3 曲线的极坐标方程1.4 圆的极坐标方程1.4.1 圆心在极轴上且过极点的圆1.4.2 圆心在点( a,∏ /2 )处且过极点的圆1.5 柱坐标系和球坐标系1.5.1 柱坐标系1.5.2 球坐标系第二章参数方程2.1 曲线的参数方程2.1.1 抛射体的运动2.1.2 曲线的参数方程2.2 直线与圆的参数方程2.2.1 直线的参数方程2.2.2 圆的参数方程2.3 圆锥曲线的参数方程2.3.1 椭圆的参数方程2.3.2 双曲线的参数方程2.3.3 抛物线的参数方程2.4 一些常有曲线的参数方程2.4.1 摆线的参数方程2.4.2 圆的渐开线的参数方程。
七年级上册数学第三章代数式知识点一、代数式的概念。
1. 定义。
- 由数和表示数的字母经有限次加、减、乘、除、乘方和开方等代数运算所得的式子,或含有字母的数学表达式称为代数式。
例如:2x + 3,a^2 - b,(1)/(x)(x≠0)等都是代数式。
单独的一个数或者一个字母也是代数式,比如5,a等。
2. 代数式与等式、不等式的区别。
- 等式是表示两个代数式相等关系的式子,用“=”连接,如2x+3 = 5x - 1;不等式是表示两个代数式大小关系的式子,用“>”“<”“≥”“≤”连接,如3x+1>2x - 2。
而代数式不含有这些关系符号。
二、代数式的分类。
1. 整式。
- 单项式。
- 定义:由数与字母的积组成的代数式叫做单项式,单独的一个数或一个字母也叫做单项式。
例如:-3xy,4a,5等都是单项式。
- 系数:单项式中的数字因数叫做这个单项式的系数。
例如在单项式-3xy 中,系数是-3;在单项式4a中,系数是4;单项式5的系数就是5。
- 次数:一个单项式中,所有字母的指数的和叫做这个单项式的次数。
例如在单项式-3xy中,x的次数是1,y的次数是1,所以单项式-3xy的次数是1 + 1=2;单项式4a的次数是1。
- 多项式。
- 定义:几个单项式的和叫做多项式。
例如2x+3y,x^2 - 2x + 1等都是多项式。
- 项:在多项式中,每个单项式叫做多项式的项,其中不含字母的项叫做常数项。
例如在多项式x^2 - 2x+1中,x^2、-2x、1都是它的项,1是常数项。
- 次数:多项式里次数最高项的次数,叫做这个多项式的次数。
例如在多项式x^2 - 2x + 1中,次数最高的项是x^2,其次数为2,所以这个多项式的次数是2。
2. 分式。
- 定义:一般地,如果A、B(B≠0)表示两个整式,且B中含有字母,那么式子(A)/(B)就叫做分式。
例如(1)/(x),(x + 1)/(x - 1)等都是分式。
利息理论第三章课后答案《金融数学》课后习题参考答案第三章 收益率1、某现金流为:3000o o =元,11000o =元,12000I =元,24000I =元,求该现金流的收益率。
解:由题意得:2001122()()()0O I O I v O I v -+-+-=23000100040000v v --=4133v i ⇒=⇒=2、某投资者第一年末投资7000元,第二年末投资1000元,而在第一、三年末分别收回4000元和5500元,计算利率为0.09及0.1时的现金流现值,并计算该现金流的内部收益率。
解:由题意得:23(0)[(47) 5.5]1000V v v v =--+⨯ 当0.09i =时,(0)75.05V =当0.1i =时,(0)57.85V =-令(0)00.8350.198V v i =⇒=⇒=3、某项贷款1000元,每年计息4次的年名义利率为12%,若第一年后还款400元,第5年后还款800元,余下部分在第7年后还清,计算最后一次还款额。
解:由题意得:40.121(1)0.88854i v +=+⇒=571000400800657.86v pv p =++⇒= 4、甲获得100000元保险金,若他用这笔保险金购买10年期期末付年金,每年可得15380元,若购买20年期期末付年金,则每年可得10720元,这两种年金基于相同的利率i ,计算i 。
解:由题意得: 08688.010720153802010=⇒=i a a i i5、某投资基金按1(1)t k t k δ=+-积累,01t ≤≤,在时刻0基金中有10万元,在时刻1基金中有11万元,一年中只有2次现金流,第一次在时刻0.25时投入15000元,第二次在时刻0.75时收回2万元,计算k 。
解:由题意得:101(1)1k dt t k ek +-⎰=+ 10.251(1)10.75k dt t k ek +-⎰=+ 10.751(1)10.25kdt t k e k +-⎰=+ ⇒10000(1)15000(10.75)20000(10.25)1100000.141176k k k k +++-+=⇒=6、某投资业务中,直接投资的利率为8%,投资所得利息的再投资利率为4%,某人为在第10年末获得本息和1万元,采取每年末投资相等的一笔款项,共10年,求证每年投资的款项为:100.0410000210s -。