第五讲图形与坐标、一次函数、反比例函数
- 格式:doc
- 大小:1.08 MB
- 文档页数:12

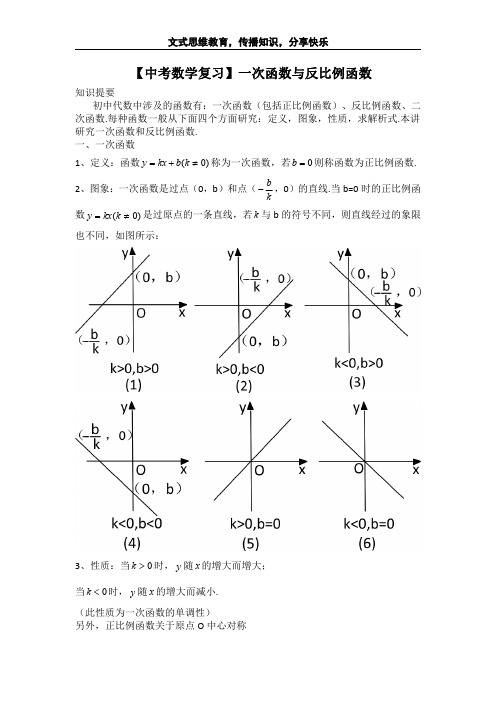
【中考数学复习】一次函数与反比例函数知识提要初中代数中涉及的函数有:一次函数(包括正比例函数)、反比例函数、二次函数.每种函数一般从下面四个方面研究:定义,图象,性质,求解析式.本讲研究一次函数和反比例函数.一、一次函数1、定义:函数)0(≠+=k b kx y 称为一次函数,若0=b 则称函数为正比例函数.2、图象:一次函数是过点(0,b )和点(kb -,0)的直线.当b=0时的正比例函数)0(≠=k kx y 是过原点的一条直线,若k 与b 的符号不同,则直线经过的象限也不同,如图所示:3、性质:当0>k 时,y 随x 的增大而增大;当0<k 时,y 随x 的增大而减小.(此性质为一次函数的单调性)另外,正比例函数关于原点O 中心对称4、求解析式:求一次函数的解析式,一般需要两个条件,求出表达式b kx y +=中的k 及b 的值,常用待定系数法来求一次函数.而正比例函数的解析式只需要一个条件.二、反比例函数1、定义:形如)0(≠=k x k y 形式称为反比例函数,定义域为0≠x 的所有实数.2、图象:反比例图象为双曲线,如图所示:3、性质:反比例函数x k y =在0>k 且0>x 时,函数值y 随x 的增大而减小;在0>k 且0<x 时,函数值y 随x 的增大而减小.即:当0>k 时,反比例函数x k y =分布在一、三象限,在每个象限内,y 随x 的增大而减小,如图(1)所示.当0<k 时,反比例函数xk y =分布在二、四象限,在每个象限内,y 随x 的增大而增大,如图(2)所示.反比例函数x k y =图象上的点关于原点O 成中心对称的.当0>k 时,函数的图象关于直线x y =成轴对称;当0<k 时,函数的图象关于直线x y -=成轴对称.4、求解析式:反比例函数的解析式,只需要一个条件,求出xk y =)0(≠k 中的k 即可.在解决有关一次函数及反比例函数的问题时,常运用数形结合及分类讨论的思想方法.待定系数法是研究函数表达式的基本方法,同时紧密结合图象寻求思路,是处理这类问题的重要方法.例1、已知正比例函数x y =和)0(>=a ax y 的图象与反比例函数xky =(k>0)的图象在第一象限内分别相交于A 、B 两点,过A 、B 作x 轴的垂线,垂足分别为C 、D ,设△AOC 和△BOD 的面积分别为1S 、2S ,则1S 与2S 的大小关系怎样?例2、两个反比例函数x y 3=,x y 6=在第一象限内的图象如图所示,点1P ,2P ,3P ,…2005P 在反比例函数x y 6=图象上,它们的横坐标分别是1x ,2x ,3x ,…2005x ,纵坐标分别是1,3,5,…,共2005个连续奇数,过点1P ,2P ,3P ,…2005P 分别作y 轴的平行线,与xy 3=的图象交点依次是)(111y x Q ,,)(222y x Q ,,)(333y x Q ,,…)(200520052005y x Q ,,则_________2005=y .例3、平面直角坐标系内有A (2,-1)、B (3,3)两点,点P 是y 轴上一动点,求P 到A 、B 距离之和最小时的坐标.例4、已知一次函数的图象经过点(2,2),它与两坐标轴所围成的三角形的面积等于1,求这个一次函数的解析式.例5、已知A (-2,0)、B (4,0),点P 在直线221+=x y 上,若△PAB 是直角三角形,求点P 的坐标.例6、已知两人连续6年对某县农村甲鱼养殖业的规模(产量)进行调查,提供两个方面的信息,如图所示,请根据图中提供的信息,求:(1)第2年全县生产甲鱼的只数及甲鱼池的个数;(2)到第6年,这个县的甲鱼养殖规模比第1年是扩大了还是缩小了,请说明理由.例7、如图,已知C 、D 是双曲线xm y =在第一象限内的分支上的两点,直线CD 分别交x 轴、y 轴于A 、B 两点,设C 、D 的坐标分别是(11y x ,)、(22y x ,),连接OC 、OD.(1)求证:111y m y OC y +<<;(2)若α=∠=∠AOD BOC ,31tan =α,10=OC ,求直线CD 的解析式.(3)在(2)的条件下,双曲线是否存在一点P ,使POD POC S S ∆∆=?若存在,求出P 点坐标;若不存在,请说明理由.例8、有一个附有进、出水管的容器,每单位时间进、出的水量都是一定的,设从某时刻开始5分钟内只进水不出水,在随后的15分钟内既进水又出水,得到时间x (分)与水量y (升)之间的关系如图所示,若20分钟后只放水不进水,求多长时间能将水放完?例9、为了预防流感,某学校对教室用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y (毫克)与时间x (分钟)成正比例,药物燃烧后,y 与x 成反比例(如图),观测得药物8分钟燃毕,此时室内空气中每立方米的含药量为6毫克,请根据题中提供的信息解答下列问题:(1)药物燃烧时,y 关于x 的函数关系式为__________,自变量x 的取值范围是___________;药物燃烧后y 关于x 的函数关系式为____________.(2)研究表明,当空气中的每立方米含药量低于1.6毫克时,学生方可进教室,那么从消毒开始,至少需要经过多少分钟后,学生才能回到教室.(3)研究表示,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?例10、某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按120个工时计算)生产空调器、彩电、冰箱共360台,且冰箱至少生产60台,已知生产这些家电产品每台所需工时和每台产值如下表所示:家电名称空调器彩电冰箱工时/个213141产值/千元432问每周应生产空调器、彩电、冰箱各多少台,才能使产值最高?最高产值是多少?(以千元为单位)练习1、已知0≠abc 并且p b a c a c b c b a =+=+=+而直线p px y +=一定通过()A 第一、二象限B 第二、三象限C 第三、四象限D 第一、四象限2、函数kx y =和)0(<=k x k y 在同一坐标系中的图象是()3、一次函数b kx y +=过点)(11y x ,和)(22y x ,,且0>k ,b<0,当210x x <<时,有()A 21y b y >>B 21y b y <<C b y y <<<210D 012<<<y b y 4、若点(-2,1y ),(1,2y ),(2,3y )在反比例函数x y 21=的图象上,则下列结论正确的是()A 123y y y >>B 312y y y >>C 132y y y >>D 321y y y >>5、反比例函数x k y =的图象是轴对称图形,它的一条对称轴是下列正比例函数图象中的()A kxy -=B x k y =C x k k y =D kxy =6、一个一次函数图象与直线49545+=x y 平行,与x 轴、y 轴的交点分别为A 、B ,并且过点(-1,-25),则在线段AB 上(包括端点A 、B ),横、纵坐标都是整数的点有()A 4个B 5个C 6个D 7个7、如图,正比例函数x y 3=的图象与反比例函数xk y =(0>k )的图象交于点A ,若取k 为1,2,3,…,20,对应的Rt △AOB 的面积分别为1S ,2S ,…20S ,则__________2021=+++S S S .8、不论k 为何值,解析式0)11()3()12(=--+--k y k x k 表示函数的图象都经过一定点,则这个定点是_________.9、如图所示,直线l 和双曲线x k y =(0>k )交于A 、B 两点,P 是线段AB 上的点(不与A 、B 重合),过点A 、B 、P 分别向x轴作垂线,垂足分别为C 、D 、E ,连接OA 、OB 、OP.设△AOC 的面积为1S ,△BOD 的面积为2S ,△POE 的面积为3S ,则321S S S 、、的大小关系是______________.10、甲、乙两车出发后再同一条公路行驶,行驶路程与时间的关系如图所示,那么可以知道:(1)出发行驶在前面的车是_________,此时两车相隔_________;(2)两车的速度分别为甲:___________千米/小时,乙:_________千米/小时,经过___________小时,快车追上慢车;(3)甲、乙两车均行驶600千米时各用的时间分别是:甲用_________小时,乙用__________小时.11、如图,函数221+-=x y 的图象交y 轴于M ,交x 轴于N ,MN 上两点A ,B 在x 轴上射影分别为11B A 、,若411>+OB OA ,则A OA 1∆的面积1S 与B OB 1∆的面积2S 的大小关系是_____________.12、已知非负数x 、y 、z 满足323=++z y x ,433=++z y x ,则z y x w 423+-=的最大值为_________,最小值为__________.13、在直角坐标系中,有四个点:A (-8,3),B (-4,5),C (0,n ),D (m ,0),当四边形ABCD 的周长最短时,求nm 的值.14、设直线1)1(=++y k kx (k 是自然数)与两坐标轴所围成的图形的面积为1S ,2S ,…,2000S .求200021S S S +++ 的值.15、如图(1),已知直线m x y +-=21与反比例函数xk y =的图象在第一象限内交于A 、B 两点(点A 在点B 的左侧),分别于x 、y 轴交于C 、D ,AE ⊥x 轴于E.(1)若OE·CE=12,求k 的值;(2)如图(2),作BF ⊥y 轴于F ,求证:EF ∥CD ;(3)在(1)(2)的条件下,5=EF ,52=AB ,P 是x 轴正半轴上一点,且△PAB 是以P 为直角顶点的等腰直角三角形,求P 点的坐标.(1)(2)16、已知直线62+-=-k y x 和143+=+k y x ,若它们的交点在第四象限内.(1)求k 的取值范围;(2)若k 为非负整数,点A 的坐标为(2,0),点P 在直线62+-=-k y x 上,求使△PAO 为等腰三角形的点P 的坐标.17、A 市、B 市和C 市分别有某种机器10台、10台和8台,现决定把这些机器支援给D 市18台,E 市10台.已知从A 市调运一台机器到D 市、E 市的运费分别为200元和800元,从B 市调运一台机器到D 市、E 市的运费分别为300元和700元,从C 市调运一台机器到D 市、E 市的运费分别为400元和500元.(1)设从A 市、B 市各调x 台到D 市,当28台机器全部调运完毕后,求总运费w (元)关于x (台)的函数式,并求w 的最大值和最小值;(2)设从A 市调x 台到D 市,从B 市调y 台到D 市,当28台机器全部调运完毕后,用x ,y 表示总运费w (元),并求w 的最大值和最小值.18、直线133+-=x y 与x 轴、y 轴分别交于点A 、B ,以线段AB 为直角边在第一象限内作等腰直角三角形ABC ,其中∠BAC=90°.如果第二象限内有一点P (a ,21),使△ABP 的面积和△ABC 的面积相等,求a 的值.文式思维教育,传播知识,分享快乐19、如图,在直角坐标系中,点1O 的坐标为(1,0),⊙1O 与x 轴交于原点O 和点A ,又点B 、C 的坐标分别为(-1,0),(0,b ),且30<<b ,直线l 是过B 、C 点的直线.(1)当点C 在线段OC 上移动时,过点1O 作l D O 直线⊥1,交l 于D ,若a S S CBO BOC=∆∆1,试求b a 与的函数关系式及a 的取值范围.20、某仓储系统有20条输入传送带、20条输出传送带.某日,控制室的电脑显示,每条输入传送带每小时进库的货物流量如图(a ),每条输出传送带每小时出库的货物流量如图(b ),而该日仓库中原有货物8吨,在0时至5时,仓库中货物存量变化情况如图(c ),则在0时至2时有多少条输入传送带在工作?在4至5时有多少条输入传送带和输出传送带在工作?。


中考总复习平面直角坐标系与一次函数反比例函数--知识讲解一、平面直角坐标系:平面直角坐标系是描述平面上点位置的一种工具,它由两条互相垂直的数轴(横轴和纵轴)构成。
横轴通常被称为x轴,纵轴通常被称为y轴。
通常,将x轴和y轴的交点称为坐标原点O。
在平面直角坐标系中,每一个点都可以用一个有序数对(x,y)来表示,其中x表示点在x轴上的位置,y表示点在y轴上的位置。
例如,点A在x轴上的位置是2,在y轴上的位置是3,那么点A的坐标就是(2,3)。
二、一次函数:1.定义:一次函数是指形如y = ax + b的函数,其中a和b是常数,并且a≠0。
其中,a叫做一次函数的斜率,b叫做一次函数的截距。
2.斜率的性质:(1)当a>0时,一次函数是递增的,意味着随着x的增加,y也增加。
(2)当a<0时,一次函数是递减的,意味着随着x的增加,y减少。
3.截距的性质:截距是指一次函数与y轴的交点,在数学上记为点(0,b)。
(1)当b>0时,一次函数与y轴正向相交,函数图像在y轴上方。
(2)当b<0时,一次函数与y轴负向相交,函数图像在y轴下方。
4.一次函数的图像特点:一次函数的图像是一条直线,直线的斜率决定了直线的倾斜程度,而截距决定了直线与y轴的交点位置。
通过改变斜率和截距的值,可以改变直线的位置和倾斜程度。
三、反比例函数:1.定义:反比例函数也称为比例函数的倒数函数,当x≠0时,反比例函数可以表示为y=k/x,其中k≠0。
反比例函数的图像是图象关于坐标原点O对称的两个分离的曲线。
2.反比例函数的性质:(1)当x增大时,y减小;当x减小时,y增大。
(2)反比例函数不存在斜线,是一对曲线对称分离的图象。
四、平面直角坐标系与一次函数反比例函数的应用:平面直角坐标系和一次函数、反比例函数可以应用于很多实际问题中,如图形的绘制、方程的求解等。
1.图形的绘制:- 对于一次函数y = ax + b,通过改变a和b的值,可以得到不同的图形及其特点。

考点五反比例函数的图像和性质知识点整合一、反比例函数的概念1.反比例函数的概念一般地,函数ky x=(k 是常数,k ≠0)叫做反比例函数.反比例函数的解析式也可以写成1y kx -=的形式.自变量x 的取值范围是x ≠0的一切实数,函数的取值范围也是一切非零实数.2.反比例函数ky x=(k 是常数,k ≠0)中x ,y 的取值范围反比例函数ky x=(k 是常数,k ≠0)的自变量x 的取值范围是不等于0的任意实数,函数值y 的取值范围也是非零实数.二、反比例函数的图象和性质1.反比例函数的图象与性质(1)图象:反比例函数的图象是双曲线,它有两个分支,这两个分支分别位于第一、三象限,或第二、四象限.由于反比例函数中自变量x ≠0,函数y ≠0,所以,它的图象与x 轴、y 轴都没有交点,即双曲线的两个分支无限接近坐标轴,但永远达不到坐标轴.(2)性质:当k >0时,函数图象的两个分支分别在第一、三象限,在每个象限内,y 随x 的增大而减小.当k <0时,函数图象的两个分支分别在第二、四象限,在每个象限内,y 随x 的增大而增大.表达式ky x=(k 是常数,k ≠0)kk >0k <0大致图象所在象限第一、三象限第二、四象限增减性在每个象限内,y随x的增大而减小在每个象限内,y随x的增大而增大2.反比例函数图象的对称性反比例函数的图象既是轴对称图形,又是中心对称图形,其对称轴为直线y=x和y=-x,对称中心为原点.3.注意(1)画反比例函数图象应多取一些点,描点越多,图象越准确,连线时,要注意用平滑的曲线连接各点.(2)随着|x|的增大,双曲线逐渐向坐标轴靠近,但永远不与坐标轴相交,因为反比例函数kyx=中x≠0且y≠0.(3)反比例函数的图象不是连续的,因此在谈到反比例函数的增减性时,都是在各自象限内的增减情况.当k>0时,在每一象限(第一、三象限)内y随x的增大而减小,但不能笼统地说当k>0时,y随x的增大而减小.同样,当k<0时,也不能笼统地说y随x 的增大而增大.三、反比例函数解析式的确定1.待定系数法确定解析式的方法仍是待定系数法,由于在反比例函数kyx=中,只有一个待定系数,因此只需要一对对应值或图象上的一个点的坐标,即可求出k的值,从而确定其解析式.2.待定系数法求反比例函数解析式的一般步骤(1)设反比例函数解析式为kyx=(k≠0);(2)把已知一对x,y的值代入解析式,得到一个关于待定系数k的方程;(3)解这个方程求出待定系数k;(4)将所求得的待定系数k的值代回所设的函数解析式.四、反比例函数中|k|的几何意义1.反比例函数图象中有关图形的面积2.涉及三角形的面积型当一次函数与反比例函数结合时,可通过面积作和或作差的形式来求解.(1)正比例函数与一次函数所围成的三角形面积.如图①,S △ABC =2S △ACO =|k |;(2)如图②,已知一次函数与反比例函数ky x=交于A 、B 两点,且一次函数与x 轴交于点C ,则S △AOB =S △AOC +S △BOC =1||2A OC y ⋅+1||2B OC y ⋅=1(||||)2A B OC y y ⋅+;(3)如图③,已知反比例函数ky x=的图象上的两点,其坐标分别为()A A x y ,,()B B x y ,,C 为AB 延长线与x 轴的交点,则S △AOB =S △AOC –S △BOC =1||2A OC y ⋅–1||2B OC y ⋅=1(||||)2A B OC y y ⋅-.五、反比例函数与一次函数的综合1.涉及自变量取值范围型当一次函数11y k x b =+与反比例函数22k y x=相交时,联立两个解析式,构造方程组,然后求出交点坐标.针对12y y >时自变量x 的取值范围,只需观察一次函数的图象高于反比例函数图象的部分所对应的x 的范围.例如,如下图,当12y y >时,x 的取值范围为A x x >或0B x x <<;同理,当12y y <时,x 的取值范围为0A x x <<或B x x <.2.求一次函数与反比例函数的交点坐标(1)从图象上看,一次函数与反比例函数的交点由k 值的符号来决定.①k 值同号,两个函数必有两个交点;②k 值异号,两个函数可能无交点,可能有一个交点,也可能有两个交点;(2)从计算上看,一次函数与反比例函数的交点主要取决于两函数所组成的方程组的解的情况.考向一反比例函数的定义1.反比例函数的表达式中,等号左边是函数值y ,等号右边是关于自变量x 的分式,分子是不为零的常数k ,分母不能是多项式,只能是x 的一次单项式.2.反比例函数的一般形式的结构特征:①k ≠0;②以分式形式呈现;③在分母中x 的指数为-1典例引领变式拓展故答案为:2.考向二反比例函数的图象和性质当k>0时,函数的图象在第一、三象限,在每个象限内,曲线从左向右下降,也就是在每个象限内,y随x的增大而减小.当k<0时,函数的图象在第二、四象限,在每个象限内,曲线从左向右上升,也就是在每个象限内,y随x的增大而增大.双曲线是由两个分支组成的,一般不说两个分支经过第一、三象限(或第二、四象限),而说图象的两个分支分别在第一、三象限(或第二、四象限).典例引领根据图象可知,114x x>+的解集是-正确的有②③;故选:B .【点睛】本题考查了反比例函数的性质,平移的性质,反比例函数图象与几何变换,掌握性质,数形结合是解题的关键.2.如图,点(1,2)A 和点(,)B a b 是反比例函数右侧,则下列说法中,不正确的是(A .该反比例函数解析式B .矩形OCBD 的面积为C .该反比例函数的另一个分支在第三象限,且【详解】解:根据题意,10k ->,解得1k <,∴0k =满足题意,故选:D .变式拓展二、填空题三、解答题把上表中的坐标系中描出这些点,并用光滑的曲线连接起来,得到如图所示的(1)请在该平面直角坐标系中作出(2)观察函数图象,并结合表中的数据:①猜测1y与x之间的函数关系,并求②求2y关于x的函数表达式;(2)①观察表格可知,1y 是x 设1k y x=,把()30,10代入得:1030k =,∴300k =,∴612x ≤≤.考向三反比例函数解析式的确定1.反比例函数的解析式k y x=(k ≠0)中,只有一个待定系数k ,确定了k 值,也就确定了反比例函数,因此要确定反比例函数的解析式,只需给出一对x ,y 的对应值或图象上一个点的坐标,代入k y x=中即可.2.确定点是否在反比例函数图象上的方法:(1)把点的横坐标代入解析式,求出y 的值,若所求值等于点的纵坐标,则点在图象上;若所求值不等于点的纵坐标,则点不在图象上.(2)把点的横、纵坐标相乘,若乘积等于k ,则点在图象上,若乘积不等于k ,则点不在图象上.典例引领【答案】30【分析】此题主要考查了平移的性质和反比例函数图象上点的坐标特征,题关键.利用平行四边形的面积公式得出得出k 的值.【详解】∵将该函数图像向上平移x 【答案】52【分析】本题主要考查了矩形的性质及待定系数法求反比例函数解析式,根据矩形的边与y 轴平行,()1,B m ,D【答案】8 yx =【分析】本题主要考查了求反比例函数解析式、正方形的性质等知识点,确定点是解题的关键.先根据坐标与图形得到A【答案】5 yx =-【分析】本题考查反比例函数图像的性质,键.变式拓展【答案】28【分析】利用反比例函数图像上的坐标特点,即可得出答案.【详解】解:∵ABCD 是矩形,∴90DAB ABC ∠∠==【答案】24a <<【分析】本题考查利用待定系数法求反比例函数解析式,及解不等式.先求出双曲线解析式,由题意可用长.再由线段BC 与双曲线有交点且与点考向四反比例函数中k的几何意义三角形的面积与k的关系(1)因为反比例函数kyx=中的k有正负之分,所以在利用解析式求矩形或三角形的面积时,都应加上绝对值符号.(2)若三角形的面积为12|k|,满足条件的三角形的三个顶点分别为原点,反比例函数图象上一点及过此点向坐标轴所作垂线的垂足.典例引领A .4-B .6【答案】C 【分析】本题考查反比例函数与一次函数的交点问题,题的关键.利用APC 与PBD 相似即可解决问题.【详解】解:PC x ⊥ 轴,PD ⊥PDB PCA ∴∠=∠,PD x 轴,BPD PAC ∴∠=∠,APC PBD ∴ ∽,∴AC PC PD BD=.二、填空题【答案】-3【分析】本题考查的是反比例函数系数k 的几何意义,的面积是是解答此题的关键.作AD OB ⊥OA =12OB ,然后通过证得AOD BOA ∽何意义即可求得k 的值.∵Rt OAB 中,30ABO ∠=︒,∴OA =12OB ,∵90ADO OAB ∠∠==︒,AOD BOA ∠∠=∴AOD BOA ∽,∴214AOD S OA S OB ⎛⎫== ⎪⎝⎭ ,【答案】5-【分析】此题主要考查了反比例函数的图象,比例函数的图象,理解反比例函数比例系数的几何意义是解决问题的关键.连接AB y ∥轴,得ABC 和AB y ∥轴,ABC ∴ 和AOB ∆关于AB 边上的高相等,52ABC AOB S S ∆∆∴==,根据反比例函数比例系数的几何意义得:变式拓展(1)用含m 的代数式表示(2)若3OMN S =△,则【答案】24m k =90OAB ∠=︒,∴N 点的横坐标为m ,反比例函数()0k y x x=>的图象过点N ,∴N 点的纵坐标为4m , OME OAN S S =△△,OMN OME OAN MEAN MEAN S S S S S=+-=△△△梯形梯形,3OMN S =△,三、解答题【答案】(2,4)C 或(8,1)C 【分析】本题考查了反比例函数的图象与性质,形的判定与性质;由反比例函数的对称性得四边形设点8,C m m ⎛⎫ ⎪⎝⎭,分别过点∵点A 、C 在反比例函数∴1842AOE COF S S ∆∆==⨯=,当04m <<时,则AOE S ∆∴6ACFE AOC S S ∆==梯形,k=【答案】6【分析】本题考查了反比例函数⊥轴,垂足为点E,连接等.作AE x到三角形AOB的面积,两个面积之和为⊥轴,垂足为点【详解】解:作AE x,AE x⊥轴,AB AC=∴=,BE CE,=5OC OB(1)求k和m的値;(2)当8x≥时,求函数值【答案】(1)10k=,m(2)5 04y<≤.考向五反比例函数与一次函数的综合反比例函数与一次函数综合的主要题型:(1)利用k值与图象的位置的关系,综合确定系数符号或图象位置;(2)已知直线与双曲线表达式求交点坐标;(3)用待定系数法确定直线与双曲线的表达式;(4)应用函数图象性质比较一次函数值与反比例函数值的大小等.解题时,一定要灵活运用一次函数与反比例函数的知识,并结合图象分析、解答问题.典例引领(1)若2k =,4b =-,则(2)若CE DE =,则b 与【答案】12k +【分析】本题考查了一次函数和反比例函数的交点问题,系是解此题的关键.【答案】12【分析】本题主要考查了反比例函数的综合应用,解析式,解题的关键是数形结合,熟练掌握相关的性质.过点⊥轴于点E,过点CB作BE x()DE=---=,证明AD∥132联立43y x y x =+⎧⎪⎨=-⎪⎩,解得:1131x y =-⎧⎨=⎩,2113x y =-⎧⎨=⎩,∴()3,1A -,()1,3B -,二、解答题(1)求反比例函数与一次函数的函数表达式;(2)连接OA OB ,,求OAB 的面积;(3)请结合图象直接写出不等式m kx b x+<【答案】(1)6y x =,y =x +1(2)52AOB S =对于1y x =+,当0y =时,=1x -;当0x =∴()1,0C -,()0,1D ∴1,OC =1,OD =∴111112*********AOB S =⨯⨯+⨯⨯+⨯⨯=+ (3)解:由图象可知:不等式m kx b x+<的解集为:(1)求反比例函数和一次函数的解析式;(2)设D 为线段AC 上的一个动点(不包括图象于点E ,当CDE 的面积最大时,求点【答案】(1)反比例函数解析式为y =(2)点E 坐标为()2,3-.变式拓展(1)求一次函数和反比例函数的解析式;(2)求AOB 的面积;(3)观察图象,直接写出不等式【答案】(1)y x =--(2)6(3)<4x -或02x <<【分析】(1)先把点A 代入反比例函数解析式,即可求出(2)先求出直线y =-(3)观察函数图象即可求得不等式的解集.【详解】(1)解:∵(A(1)求一次函数和反比例函数的关系式;(2)若点E 是点C 关于x 轴的对称点,求【答案】(1)一次函数解析式1y x 4=-(2)32ABE S =△【分析】(1)利用点A 的坐标,代入可求出反比例函数解析式,进而求出点待定系数法可求出一次函数的解析式;当点P在BC上运动时,则PB∵2sin ==2PH B PB ,即PH =∴(1132822y DB PH =⋅=⨯⋅()304;x x ⎧≤≤由图像可得,函数图像有最大值为(3)解:根据函数图像可得:当【点睛】本题主要考查了函数图像与性质、求函数解析式、画函数图像、三角形面积、运用函数图像解不等式等知识点,求得函数解析式以及数形结合思想是解题的关键.(1)求反比例函数和一次函数的解析式;的面积;(2)求ABO(1)求a ,k 的值.(2)利用图像信息,直接写出不等式1102k x x+-≥的解集(3)如图2,直线CD 过点A ,与反比例函数图像交于点C ,与x 轴交于点,OA OC ,求OAC 的面积.【答案】(1)4a =,12k =;(2)4x ≥(1)求一次函数和反比例函数的解析式;(2)在y轴上取一点N,当(3)将直线1y向下平移2围.根据函数图象可得:当11.如图,在平面直角坐标系例函数2myx=(m为常数,且(1)求反比例函数与一次函数的解析式.(1)求反比例函数的解析式;(2)点C在这个反比例函数图象上,坐标.【答案】(1)8 yx =(2)()4,2 C90∠=∠=∠=ABO BOE AEO∴四边形ABOE是矩形,∴==,OB AE2OE AB==45,∠=︒ADO∴ 是等腰直角三角形,AED∴==,DE AE4。

中考复习——平面直角坐标系、一次函数、反比例函数【知识梳理】一、平面直角坐标系1. 坐标平面上的点与 有序实数对 构成一一对应;2. 各象限点的坐标的符号;3. 坐标轴上的点的坐标特征.4. 点P (a ,b )关于x 轴对称的点的坐标为 ;关于y 轴对称的点的坐标为 ;关于原点对称的点的坐标为5.两点之间的距离二、函数的概念1.概念:在一个变化过程中有两个变量x 与y ,如果对于x 的每一个值,y 都有 的值与它对应,那么就说x 是自变量,y 是x 的函数.2.自变量的取值范围: (1)使解析式 (2)实际问题具有 意义3.函数的表示方法; (1) (2) (3) 三、一次函数的概念、图象、性质1.正比例函数的一般形式是 ( ),一次函数的一般形式是 (k≠0). 2. 一次函数y kx b =+的图象是经过( , )和( , )两点的一条直线.4.若两个一次函数解析式中,k 相等,表示两直线 ;若两直线垂直,则 。
5.的大小决定直线的倾斜程度,越大,直线越 ;四、反比例函数的概念、图象、性质1.反比例函数:一般地,如果两个变量x 、y 之间的关系可以表示成y = 或 或 (k 为常数,k≠0)的形式,那么称y 是x 的反比例函数. 2. 反比例函数的图象和性质k >0,b >0k >0,b <0k <0,b >0k <0,21212211P P )0()0()2(y y y P y P -=, ,,,21212211P P )0()0()1(x x x P x P -=, , ,, 3.k 的几何含义:反比例函数y =k x(k≠0)中比例系数k 的几何意义,即过双曲线y =k x(k≠0)上任意一点P 作x 轴、y 轴垂线,设垂足分别为A 、B ,则所得矩形OAPB 的面积为 。
【例题精讲】 例1.函数22y x =-中自变量x 的取值范围是 ;函数y =x 的取值范围是 .例2.已知点(13)A m -,与点(21)B n +,关于x 轴对称,则m = ,n = . 例3.如图,在平面直角坐标系中,点A 的坐标是(10,0),点B 的 坐标为(8,0),点C 、D 在以OA 为直径的半圆M 上,且四边形OCDB 是平行四边形,点C 的坐标为例4.一次函数y=(3a+2)x -(4-b),求满足下列条件的a 、b 的取值范围。
正比例函数、一次函数、反比例函数的性质及图象一、正比例函数性质和图象:概念:一般地,形如(k是常数,且k≠0 )的函数,叫做正比例函数。
当k>0时,图象过象限; y随x的增大而。
当k<0时,图象过象限; y随x的增大而。
:概念:一般地,形如y=kx+b(k,b是常数,且k≠0 )的函数,叫做一次函数。
图像和性质:①k>0,b>O,则图象过象限②k>0,b<0,则图象过象限当k>0时, y随x的增大而。
③k<0,b>0,则图象过象限④k<0,b<0,则图象过象限当k<0时, y随x的增大而。
三、反比例函数性质和图象:1.定义:形如(k为常数,k≠0)的函数称为反比例函数。
其他形式2.图像:反比例函数的图像是双曲线。
反比例函数的图象既是轴对称图形又是中心对称图形。
3.性质:当k>0时双曲线的两支分别位于,在每个象限内y值随x值的增大而减小。
当k<0时双曲线的两支分别位于,在每个象限内y 值随x值的增大而增大。
4.|k|的几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积。
练习题 1、若y =(m -1)x22m -是正比例函数,则m 的值为( ) A 、1 B 、-1 C 、1或-1 D 、2或-2 2、下列函数中,一次函数为( )A 、25y x = B .25y x =-1 C .245y x = D .25y x=-3、下列函数中,反比例函数是( )A 、y=x+1B 、y=C 、=1D 、3xy=24、正比例函数y=kx (k ≠0)函数值y 随x 的增大而增大,则y=kx+k 的图象大致是( )5、直线443--=x y 与两坐标轴围成的三角形面积是( ) A 3 B 4 C 12 D 66、函数y 1=kx 和y 2=的图象如图,自变量x 的取值范围相同的是( )7、若点A(x 1,1)、B(x 2,2)、C(x 3,-3)在双曲线上,( )A 、x 1>x 2>x 3B 、x 1>x 3>x 2C 、x 3>x 2>x 1D 、x 3>x 1>x 28、已知一次函数y=ax+b 图象在一、二、三象限,则反比例函数y=的函数值随x 的增大而__________。
中考数学《一次函数》《二次函数》《反比例函数》考点分析及专题训练函数及其图象1、坐标与象限定义1:我们把有顺序的两个数a与b所组成的数对,叫做有序数对,记作(a,b)。
定义2:平面直角坐标系即在平面内画互相垂直,原点重合的两条数轴。
水平的数轴称为x轴或横轴,取向右方向为正方向;竖直的数轴称为y轴或纵轴,取向上方向为正方向。
两坐标轴的交点为平面直角坐标系的原点。
建立平面直角坐标系后,坐标平面被两条坐标轴分成了四个部分,每个部分称为象限,分别叫做第一象限、第二象限、第三象限、第四象限,坐标轴上的点不属于任何象限。
2、函数与图象定义1:在一个变化过程中,我们称数值发生变化的量为变量,数值始终不变的量为常量。
定义2:一般地,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数。
如果当x=a时,y=b,那么b叫做当自变量的值为a时的函数值。
定义3:一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象。
定义4:用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数的常用方法。
这种式子叫做函数的解析式。
表示函数的方法:解析式法、列表法和图象法。
解析式法可以明显地表示对应规律;列表法直接给出部分函数值;图象法能直观地表示变化趋势。
画函数图象的方法——描点法:第1步,列表。
表中给出一些自变量的值及其对应的函数值;第2步,描点。
在直角坐标系中,以自变量的值为横坐标、相应的函数值为纵坐标,描出表格中数值对应的各点;第3步,连线。
按照横坐标由小到大的顺序,把所描出的各点用平滑曲线连接起来。
1、结合实例进一步体会用有序数对可以表示物体的位置。
2、理解平面直角坐标系的有关概念,能画出直角坐标系;在给定的直角坐标系中,能根据坐标描出点的位置、由点的位置写出它的坐标。
一次函数知识点总结:函数性质:1. y的变化值与对应的x的变化值成正比例,比值为k. 即:y=kx+b(k,b为常数,k≠0)当x增加m,k(x+m)+b=y+km, km/m=k。
2. 当x=0时,b为函数在y轴上的点,坐标为(0,b)。
3. 当b=0时(即y=kx),一次函数图像变为正比例函数,正比例函数是特殊的一次函数。
4. 一次函数的图像:直线5. 在两个一次函数表达式中:当两一次函数表达式中的k相同,b也相同时,两一次函数图像重合;当两一次函数表达式中的k相同,b不相同时,两一次函数图像平行;当两一次函数表达式中的k不相同,b不相同时,两一次函数图像相交;当两一次函数表达式中的k不相同,b相同时,两一次函数图像交于y轴上的同一点(0,b)。
若两个变量x,y间的关系式可以表示成Y=KX+b(k,b为常数,k不等于0)则称y是x的一次函数图像性质1.作法与图形:通过如下3个步骤:(1)列表.(2)描点;[一般取两个点,根据“两点确定一条直线”的道理,也可叫“两点法”。
一般的y=kx+b(k≠0)的图象过(0,b)和(-b/k,0)两点画直线即可。
正比例函数y=kx(k≠0)的图象是过坐标原点的一条直线,一般取(0,0)和(1,k)两点。
(3)连线,可以作出一次函数的图象——一条直线。
因此,作一次函数的图象只需知道2点,并连成直线即可。
(通常找函数图象与x轴和y轴的交点分别是-k分之b与0,0与b).2.性质:(1)在一次函数上的任意一点P(x,y),都满足等式:y=kx+b(k≠0)。
(2)一次函数与y轴交点的坐标总是(0,b),与x轴总是交于(-b/k,0)正比例函数的图像都是过原点。
3.函数不是数,它是指某一变化过程中两个变量之间的关系。
4.k,b与函数图像所在象限:y=kx时(即b等于0,y与x成正比例):当k>0时,直线必通过第一、三象限,y随x的增大而增大;当k<0时,直线必通过第二、四象限,y随x的增大而减小。
反比例函数1、反比例函数图象:反比例函数的图像属于以原点为对称中心的中心对称的双曲线反比例函数图像中每一象限的每一支曲线会无限接近X轴Y轴但不会与坐标轴相交(K≠0)。
2、性质:1.当k>0时,图象分别位于第一、三象限,同一个象限内,y随x的增大而减小;当k<0时,图象分别位于二、四象限,同一个象限内,y随x的增大而增大。
2.k>0时,函数在x<0上同为减函数、在x>0上同为减函数;k<0时,函数在x<0上为增函数、在x>0上同为增函数。
定义域为x≠0;值域为y≠0。
3.因为在y=k/x(k≠0)中,x不能为0,y也不能为0,所以反比例函数的图象不可能与x轴相交,也不可能与y轴相交。
4. 在一个反比例函数图象上任取两点P,Q,过点P,Q分别作x轴,y轴的平行线,与坐标轴围成的矩形面积为S1,S2则S1=S2=|K|5. 反比例函数的图象既是轴对称图形,又是中心对称图形,它有两条对称轴 y=x y=-x(即第一三,二四象限角平分线),对称中心是坐标原点。
6.若设正比例函数y=mx与反比例函数y=n/x交于A、B两点(m、n同号),那么A B两点关于原点对称。
7.设在平面内有反比例函数y=k/x和一次函数y=mx+n,要使它们有公共交点,则n^2+4k·m≥(不小于)0。
8.反比例函数y=k/x的渐近线:x轴与y轴。
9.反比例函数关于正比例函数y=x,y=-x轴对称,并且关于原点中心对称.10.反比例上一点m向x、y分别做垂线,交于q、w,则矩形mwqo(o为原点)的面积为|k|11.k值相等的反比例函数重合,k值不相等的反比例函数永不相交。
12.|k|越大,反比例函数的图象离坐标轴的距离越远。
13.反比例函数图象是中心对称图形,对称中心是原点一次函数(一)函数1、确定函数定义域的方法:(1)关系式为整式时,函数定义域为全体实数; (2)关系式含有分式时,分式的分母不等于零;(3)关系式含有二次根式时,被开放方数大于等于零; (4)关系式中含有指数为零的式子时,底数不等于零;(5)实际问题中,函数定义域还要和实际情况相符合,使之有意义。
第五讲 图形与坐标、一次函数、反比例函数§5.1 图形与坐标知识梳理1. 坐标平面内点的坐标特征⑴第一象限内的点, 横坐标为 , 纵坐标为 ; 第二象限内的点, 横坐标为 , 纵坐标为 ; 第三象限内的点, 横坐标为 , 纵坐标为 ; 第四象限内的点, 横坐标为 , 纵坐标为 .⑵x 轴上的点, 纵坐标为 ; y 轴上的点, 横坐标为 . 上的点不属于任何象限. 既在x 轴上又在y 轴上的点的坐标为 .⑶关于x 轴对称的两点, 横坐标 , 纵坐标 ; 关于y 轴对称的两点横坐标 , 纵坐标 ; 关于原点对称的两点的横坐标 , 纵坐标 .⑷平行于x 轴 (或垂直于y 轴)的直线上点的纵坐标 , 横坐标为 ; 平行于y 轴(或垂直于x 轴)的直线上点的横坐标 , 纵坐标为 .⑸第一、三象限角平分线上的点的横坐标与纵坐标 ; 第二、四象限角平分线上的点的横坐标与纵坐标 .(6) 坐标平面内的点与有序实数对是 对应的. 2. 坐标与图形平移⑴在平面直角坐标系中,将点()y x ,向右(或向左)平移m 个单位长度,可以得到对应点是 (或 ); 在平面直角坐标系中,将点()y x ,向上(或向下)平移n 个单位长度,可以得到对应点是 (或 ).⑵对于一个图形平移, 这个图形上所有 都要发生相应的变化; 反过来, 从图形上的 的某种变化也可以看出对这个图形进行了怎样的平移.考点呈现考点1 坐标平面内的点与象限例1 (2012年山东荷泽)点()1,2-在平面直角坐标系中所在的象限是 ( )A.第一象限B.第二象限C.第三象限D.第四象限解析: 因为横坐标为2-,这样的点在二、三象限, 而纵坐标为1, 这样的点在一、二象限, 所以点()1,2-在第二象限. 故选B.点评: 要判定点在哪个象限, 关键要掌握四个象限坐标的特特征: 第一象限的点()++,,第二象限的点()+-,,第三象限的点()--,, 第四象限的点()-+,.考点2 关于坐标轴对称的点的坐标特征例 2 (2012年深圳市) 已知点P ()1,23a a +-关于x 轴的对称点在第一象限, 则a 的取值范围是( )A.a <1-B.1-<a <23 C.23-<a <1 D.a >23解析: 由点P 关于x 轴对称的点在第一象限, 知点P 在第四象限, 于是有10,230,a a +>⎧⎨-<⎩由此解得1-<a <23. 故选B.点评: 关于x 轴对称的点的坐标横坐标相等, 纵坐标互为相反数; 关于y 轴对称的点的坐标, 横坐标相等, 纵坐标互为相反数.考点3 关于原点对称的点的坐标特征例3 (2011年浙江宁波) 平面直角坐标系中, 与点()3,2-关于原点中心对称的点是 ( )A.()2,3-B.()2,3-C.()3,2-D.()3,2答案:C.点评: 关于原点对称的两点的横坐标互为相反数, 纵坐标互为相反数. 考点4 坐标平面内的图形变换例4 (2012年山东青岛) 如图1, 将四边形ABCD 先向左平移3个单位, 再向上平移2个单位, 那么点A 的对应点'A 的坐标是 ( )A.()1,6B.()1,0C.()3,0-D.()3,6-解析: 点A ()1,3-先向左平移3个单位, 再向上平移2个单位, 得到'A 的坐标是033=-, 纵坐标是121=+-. 故选B.点评: 本题考查图形的平移变换, 点移动的规律是“左减右加, 下减上加”.误区点拨不会正确分类讨论和探索规律例 (2012年北京) 在平面直角坐标系xOy 中, 我们把横 、纵坐标都是整数的点叫做整点. 如图2,已知点A ()4,0,点B 是x 轴正半轴上的整点, 记△AOB 内部(不包括边界)的整点个数为m , 当3=m 时, 点B 的横坐标的所有可能值是 ; 当点B 的横坐标为n 4(n 为正整数)时, =m (用含n 的代数式表示).错解: 第一空填3, 第二空不会填.剖析: 不会运用分类讨论思想以及不会正确探索规律是错解或不会解答本题的根本原因. 正解: 当3=m 时, 点B 的横坐标可能是3或4, 如图2.当1=n 时, B 点的横坐标为4, 如图3, 此时3=m ; 当2=n 时, B 点的横坐标为8, 如图4, 此时9=m ; 当3=n 时, B 点的横坐标为12, 如图5, 此时15=m ; … … 于是36-=n m . 故第一空填3或4, 第二空填36-n .图2 DABC-22642O x y 图1跟踪训练1. 点M ()1,2关于x 轴对称的点的坐标是 ( )A.()2,1-B.()2,1-C.()1,2-D.()2,1- 2. 将点A ()1,2向左平移2个单位长度得到'A 点, 则'A 点的坐标是 ( )A.()3,2B.()1,2-C.()1,4D.()1,0 3. 在如图所示的平面直角坐标系内, 画在透明胶片上的平行四边形ABCD , 点A 的坐标是()2,0, 现平移这张胶片, 使点A 落在()1,5'-A 处, 则此平移可以是 ( )A. 先向右平移5个单位, 再向下平移1个单位B. 先向右平移5个单位, 再向下平移3个单位C. 先向右平移4个单位, 再向下平移1个单位D. 先向右平移4个单位, 再向下平移3个单位4. 点P ()2,3-关于x 轴对称的点'P 的坐标是 .5. 在平面直角坐标系中, 一青蛙从点A ()0,1-处向右跳2个单位长度, 再向上跳2个单位长度到点A ′处, 则点A ′的坐标为为 .6. 在平面直角坐标系中, △ABC 的三个顶点的坐标分别是A ()3,3-, B ()1,4--, C ()0,2, 将△ABC 平移至111C B A ∆的位置, 点A ,B ,C 的对应点分别是1A ,1B ,1C .若点1A 的坐标为()1,3, 则点1C 的坐标为 .图3图2图1图3 图4图5B CDAyx O第3题图§5.2 一次函数知识梳理1. 一次函数的定义一般地, 形如 的函数, 叫做一次函数. 特别的, 当0=b 时, 叫做 .由这个定义可以看出, 正比例函数是特殊的一次函数, 但一次函数不一定是正比例函数. 2. 一次函数的图象的画法一次函数b kx y +=的图象是 . 根据“两点确定一条直线”的原理, 在平面直角坐标系中, 取符合要求的两个点画出直线即可, 因此一次函数b kx y +=也叫直线b kx y +=.3. 一次函数的图象的特点一次函数b kx y +=的图象是一条不与坐标轴平行的直线. 当b >0时, 其图象与y 轴的 相交; 当b <0时, 其图象与y 轴的 相交. 正比例函数kx y =的图象是经过 的直线.4. 一次函数的图象的性质当k >0时, 图象像“撇”, y 随x 的增大而 ; 当k <0时, 图象像“捺”,y 随x 的增大而 . 6. 一次函数与方程和不等式(组)的关系⑴ 由于一元一次方程都可以化为0=+b ax (a ,b 是常数, 0≠a )的形式, 所以一元一次方程是一次函数的函数值为0的特殊形式. 利用这个关系, 可以确定一次函数与x 轴交点的 的值.⑵ 由于一元一次不等式都可以化为b ax +>0(或b ax +<0)(a 、b 是常数, 0≠a )的形式, 所以一元一次不等式是一次函数的函数值大(小)于0的特殊形式. 利用这个关系可以求一元一次不等式的 .⑶一般地, 任何一个二元一次方程组都对应着两个一次函数,也对应着两条直线. 从“数”方面看, 解方程组就是考虑当自变量为何值时, 两个函数的函数值 , 以及这个函数值是多少; 从“形”的角度看, 解方程就是求两条直线的交点的 .考点呈现考点1 一次函数的概念例1 ( 2012年四川南充) 下列函数中,是正比例函数的是 ( )A.x y 8-=B.xy 8-= C.652+=x y D.15.0--=x y 解析: xy 8-=是反比例函数, 652+=x y 是二次函数, 15.0--=x y 是一次函数但不是正比例函数, 只有A 选项符合正比例函数的定义, 故选A..点评: 正确理解正比例函数定义是解答本题的关键, 要明确正比例函数图象是经过原点的直线. 考点2 用待定系数法求一次函数的解析式例2 ( 2012年山东荷泽) 如图1, 一次函数232+-=x y 的图象分别与x 轴、y 轴交于点A 、B , 以线段AB 为边在第一象限内作等腰Rt △ABC , ∠BAC=90, 求过B ,C 两点直线的解析式.解析: 易知直线232+-=x y 与x 轴、y 轴交于点A ()0,3、B ()2,0, 故有OB=2, OA=3. 过点C 作C D ⊥x 轴于点D, 则∠CDA=090, ∠ACD+∠DCA=090.由∠AOB=090, 得∠OAB+∠DAC=090,所以∠AOB=∠CDA, ∠OAB=∠DCA.BACD xy O又AB=AC, 所以△AOB ≌△CDA , 所以CD=OA=3, AD=OB=2. 故得点C 的坐标为()3,5.设直线BC 的解析式为2+=kx y , 代入C 点的坐标, 得253+=k , 解得51=k . 所以过B,C 两点直线的解析式为251+=x y . 点评: 求一点的坐标, 先求该点到x 轴、y 轴的距离.例3 (2012年山东聊城) 如图2,直线AB 与x 轴交于点A ()0,1, 与y 轴交于点B ()2,0-. ⑴求直线AB 的解析式;⑵若直线AB 上一点C 在第一象限, 且2=∆BOC S , 求点C 的坐标.解析: ⑴设直线AB 的解析式为2-=kx y , 代入点A 的坐标()0,1, 得20-=k , 解得2=k . 所以,直线AB 的解析式为22-=x y .⑵由点C 在直线AB 上,可设点C 的坐标为()22,-m m . 由2=∆BOC S , 得2221=⨯⨯m , 解得2±=m . 因为点C 在第一象限, 所以点C 的坐标为()2,2.点评: 本题用待定系数法求一次函数解析式, 突显函数与方程结合, 函数与几何结合. 考点3 一次函数的实际应用例4 ( 2012年山东临沂) 小明家今年种植的“红灯”樱桃喜获丰收, 采摘上市20天全部销售完, 小明对销售情况进行了跟踪记录, 并将记录情况绘成图象, 日销售量y (单位:千克)与上市时间x (单位:天)的函数关系如图3所示, 樱桃价格z (单位:元/千克)与上市时间x (单位:天)的函数关系如图4所示.⑴观察图象, 直接写出日销售量的最大值; ⑵求李明家樱桃的日销售量y 与上市时间x 的函数解析式;⑶试比较第10天与第12天的销售金额哪天多?解析: ⑴120千克;⑵当0≤x ≤12时, 函数图象过原点和()120,12两点, 设日销售量y 与上市时间x 的函数解析式为kx y =,代入坐标()120,12得, k 12120=, 解得10=k , 所以日销售量y 与上市时间x 的函数解析式为x y 10=;当12<x ≤20时, 函数图象过()0,20和()120,12两点, 设日销售量y 与上市时间x 的函数解析式为n mx y +=,代入已知点的坐标得12120,200m n m n +=⎧⎨+=⎩, 解得15,300m n =-⎧⎨=⎩,所以日销售量y 与上市时间x 的函CA B xyO 图2图4图3数解析式为30015+-=x y ;⑶在图4中, 当5<x ≤15时, 函数图象过()32,5和()12,15两点, 所以可得樱桃价格z 与上市时间x 的函数解析式为422+-=x z .所以,当x=10时, 日销售量y=100千克, 樱桃价格z=22元, 销售金额为22×100=2200(元);当x=12时, 日销售量y=120千克, 樱桃价格z=18元, 销售金额为18×120=2160(元).因为2200>2160, 所以第10天的销售金额多.点评: 本题考查了一次函数的应用,是近年中考中的热点问题; 同时此函数是一个分段函数, 应注意自变量的取值范围.误区点拨函数性质掌握不清例 (2012年贵州贵阳) 在正比例函数mx y 3-=中, 函数y 的值随x 的值的增大而增大, 则P ()5,m 在第 象限.错解: 一.剖析: 此题难度不大, 但涉及的知识点较多, 包括一次函数的性质、不等式的解法、点的坐标与位置的关系等, 这些都是同学们在答题时容易出错的地方.正解: 由函数y 的值随x 的值的增大而增大, 得m 3->0,解得m <0, 所以点P ()5,m 在第二象限内. 故填“二”.跟踪训练1. 直线1-=x y 不经过 ( ) A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限2. 若直线42--=x y 与直线b x y +=4的交点在第三象限, 则b 的取值范围是 ( ) A.4-<b <8 B.4-<b <0 C.b >4-或b >8 D.84≤≤-b3. 一次函数42+-=x y 的图象与y 轴的交点坐标是 ( ) A.()4,0 B.()0,4 C.()0,2 D.()2,04. 已知一次函数b kx y +=图象过点()2,0,且与两坐标轴围成的三角形面积为2, 求此一次函数的解析式.5. 一列快车由甲地开往乙地, 一列慢车由乙地开往甲地, 两车同时出发, 匀速运动. 快车离乙地的路程1y (km )与行驶的时间x (h )之间的函数关系如图中线段AB 所示. 慢车离乙地的路程2y (km )与行驶的时间x (h )之间的函数关系, 如图中线段OC 所示. 根据图象进行以下研究.解读信息:⑴甲、乙两地之间的距离为 km ;⑵线段AB 的解析式为 , 线段OC 的解析式为 ;问题解决:⑶设快、慢车之间的距离为y (km ), 求y 与慢车行驶时间x (h )的函数解析式, 并画出函数的图象.§5.3 反比例函数识识梳理1. 反比例函数的概念: 一般地, 形如 (k 是常数, 0≠k )的函数叫做反比例函数.2. 反比例函数的图象: 反比例函数xky =的图象是 . 当k >0时,两个分支位于 ; 当k <0时, 两个分支位于 .3. 反比例函数图象的性质⑴对称性: 反比例函数xky =的图象是轴对称图形, 当k >0时,其对称轴是直线 ; 当k <0时, 其对称轴是直线 . 反比例函数xky =的图象也是中心对称图形, 其对称中心是 .⑵增减性:当k >0时, 在 内, y 随x 的增大而 ; 当k <0时, 在 内, y 随x 的增大而减小 .考点呈现考点1 反比例函数的图象与性质例1 (2012年山东青岛)点A ()11,y x 、B ()22,y x 、C ()33,y x 都在反比例函数xy 3-=的图象上, 若1x <2x <0<3x , 则1y ,2y ,3y 的大小关系是 ( )A.3y <1y <2yB.1y <2y <3yC.3y <2y <1yD.2y <1y <3y 解析: 这里3-=k <0, 所以在每个象限内y 随x 的增大而增大, 当1x <2x <0时,2y >1y >0. 又因为()33,y x 在第四象限, 所以3y <0,于是3y <1y <2y . 故选A.点评: 本题考查了反比例函数的增减性. 注意“在每个象限”这一重要条件. 考点2 利用反比例函数的图象确定k 的取值范围例2 (2012年福建福州) 如图1, 过点C ()2,1分别作x 轴、y 轴的平行线, 交直线6+-=x y 于A ,B 两点, 若反比例函数x ky =(x >0)的图象与△ABC 有公共点, 则k 的取值范围是( )A.92≤≤kB.82≤≤kCAOx/hy/km 36450Ox/hy/km36450B D备用第5题图C BA x y O图1C.52≤≤kD.85≤≤k 解析: 当点C ()2,1在反比例函数xky =(x >0)的图象上时, 则2=k . 当反比例函数与直线AB 只有一个交点时,令6+-=x xk,得062=+-k x x , 当()0462=--k , 即9=k 时, 直线与双曲线有且一个交点, 因此反比例函数xky =(x >0)的图象与△ABC 有公共点, k 的取值范围是92≤≤k .故选A.点评注: 本题通过对问题的特殊化, 考查了学生解题思维的灵活性, 还通过数形结合考查了建立方程模型解决问题的能力.考点3 反比例函数的解析式的求法例3 ( 2012年山东聊城) 如图2, 在直角坐标系中, 正方形的中心在原点O, 且正方形的一组对边与x 轴平行. 点P ()a a ,3是反比例函数xky =(k >0)的图象与正方形的一个交点. 若图中阴影部分的面积为9, 则这个反比例函数的解析式为 .解析: 由于正方形和反比例函数的图象都是中心对称图形, 结合题设可知图中阴影的面积是正方形面积的41, 由此可求得正方形的面积为36, 于是正方形的边长为6, 进而可求出点P 的横坐标为3, 由33=a , 解得1=a . 所以P ()1,3. 因为点P 在反比例函数的图象上, 所以31k =, 即3=k , 所以反比例函数的解析式为xy 3=. 点评: 本题借助正方形、反比例函数图象均为中心对称图形特点及化零为整的思想, 把复杂问题巧妙地解决, 是一道较新颖的创新题.考点4 反比例函数的应用例4 ( 2012年安徽) 甲、乙两家商场进行促销活动, 甲商场采用“满200减100”的促销方式, 即购买商品的总金额满200元但不足400元, 少付100元; 满400元但不足600元, 少付200元; ……, 乙商场按顾客购买商品的总金额打6折促销.⑴若顾客在甲商场购买了510元的商品, 付款时应付多少钱?⑵若顾客在甲商场购买商品的总金额为x (400≤x <600)元, 优惠后得到商家的优惠率为p (购买商品的总金额优惠金额=p ),写出p 与x 之间的函数关系式, 并说明p 随x 的变化情况;⑶品牌、质量、规格等都相同的某种商品, 在甲乙两商场的标价都是x (200≤x <400)元, 你认为选择哪家商场购买商品花钱较少? 请说明理由.解析: ⑴310200510=-(元);⑵xp 200=, 当400≤x <600时,p 随x 的增大而减小; ⑶购x 元(200≤x <400)在甲商场的优惠额是100元, 乙商场的优惠额是x x x 4.06.0=-. 当x 4.0<100, 即200≤x <250时, 选甲商场优惠; 当x 4.0=100, 即x =250时, 选甲乙商场一样优惠; 当x 4.0>100, 即250<x <400时, 选乙商场优惠.点评: 充分利用反比例函数变量之间的关系确定优惠范围, 而这样的优惠一般都是在一定的范围内适合, 如第⑶问.误区点拨1. 考虑问题不全图2例1 (2012年浙江衢州) 如图3, 已知函数x y 2=和函数xky =的图象交于A ,B 两点, 过点A 作AE ⊥x 轴于点E , 若△AOE 的面积为4, P 是坐标平面上的点, 且以点B 、O 、E 、P 为顶点的四边形是平行四边形, 则满足条件的P 点坐标是 .错解:()4,0-.剖析: 没有全面考虑问题, 不注意分类讨论,导致漏解. 正解: 根据反比例函数中比例系数k 的几何意义, 得出方程12|k|=4, 求出k 的值为8, 然后结合函数x y 2=和函数xky =可求出点A ()4,2,再根据平行四边形的性质可求得P 点坐标.当以OB 、OE 为一组邻边时, 可求得()4,01-P ; 当以OB 为一条对角线时, 可求得()4,42--P ; 当以OE 为一条对角线时可求得()34,4P .故填()4,0-或()4,4--或()4,4.2.自变量的实际意义不清例2 ( 2012年四川南充) 矩形的长为x ,宽为y ,面积为9, 则y 与x 之间的函数关系用图象表示大致为 ()错解: B.剖析: 根据题设可知xy 9=, 所以y 是x 的反比例函数, 由于矩形的长和宽为正数, 所以这个反比例函数的图象应该只有第一象限的一个分支.故选C.正解:C.3.性质理解不透例3 ( 2012年山东荷泽) 反比例函数xy 2=图象上的两上点为()11,y x 、()22,y x , 且1x <2x , 则下列关系成立的是 ( )A.1y >2yB.1y <2yC.21y y =D.不能确定错解: A.剖析: 没有注意反比例函数性质中“在每个象限内”这个条件.正解: 反比例函数xy 2=的图象在一、三象限, 在每个象限内y 随x 的增大而减小,因为1x <2x ,当两点分别在两个象限时1y <2y ; 当两点在同一个BA Exy O图3象限时, 1y >2y . 故选D.跟踪训练1. 已知反比例函数xm y 1-=的图象如图所示, 则实数m 的取值范围是 ( )A.m >1B.m >0C.m <1D.m <02.如图, 正方形ABOC 的边长为2, 反比例函数xky =的图象经过点A , 则k 的值是 ( )A.2B.2-C.4D.4-3. 如图, 若点M 是x 轴正半轴上的任意一点, 过点M 作PQ ∥y 轴, 分别交函数x k y 1=(x >0)和xky 2=(x >0)的图象于点P 和Q , 连接OP 、OQ , 则下列结论正确的是 ( )A.∠POQ 不可能等于090 B.21k k QM PM =C.这两个函数的图象一定关于x 轴对称D.△POQ 的面积是()2121k k + 4. 近视眼镜的度数y (度)与镜片焦距x (m )成反比例(即xky =(0≠k )), 已知200度近视眼镜的镜片焦距为m 5.0, 则y 与x 之间的函数关系式是 .5.已知反比例函数xy 2=的图象经过点A ()1,m , 则m 的值为 . 6. 据媒体报道, 近期“手足口病”可能进入发病高峰期, 某校根据《学校卫生工作条例》, 为预防“手足口病”, 对教室进行“薰药消毒”. 已知药物在燃烧机释放过程中, 室内空气中每立方米含药量y (毫克)与燃烧时间x (分钟)之间的关系如图所示(即图中线段OA 和双曲线在A 点及其右侧的部分), 根据图象所示信息, 解答下列问题:⑴写出从药物释放开始, y 与x 之间的函数关系式及自变量的取值范围;⑵据测定, 当空气中每立方米的含药量低于2毫克时, 对人体无毒害作用, 那么从消毒开始, 至少在多长时间内, 师生不能进入教室?yxO第1题图y xB OC A 第2题图第3题图第6题图跟踪训练参考答案§5.1 图形与坐标1. C2. D3. B4. ()2,3--5.()2,16. ()2,8-§5.2 一次函数1. B2. A3.A4. 解: 由题意知2=b .设一次函数的图象与x 轴的交点坐标为()0,a , 根据题意, 得2221=⨯⨯a , 解得2±=a . 将()0,2代入2+=kx y 中, 得220+=k , 解得1-=k ;将()2,0-代入2+=kx y 中, 得220+-=k , 解得1=k .所以,一次函数的解析式为2+-=x y 或2+=x y .5. 解: ⑴450;⑵设线段AB 的解析式为450+=kx y (30≤≤x ), 代入点B 的坐标()0,3, 得45030+=k , 解得150-=k ,线段AB 的解析式为450150+-=x y (30≤≤x ). 同理线段OC 的解析式为x y 75=(60≤≤x );解方程45015075+-=x x , 得2=x , 于是点D 的坐标为()150,2. 1245015075.y y y x x =-=--当20≤≤x 时, x y 225450-=;当2<3≤x 时, 450225-=x y ;当63≤≤x 时, x y 75=.画出的图象如图所示.§5.3 反比例函数1.A2.D3.D4.xy 100= 5.2 6. 解: ⑴设y 与x 之间的函数关系式为xk y =, 由图象可知点()6,25在其图象上, 故625k =, 即150=k , 所以从药物释放开始, y 与x 之间的函数关系式为x y 150=. x/hy/kmA O 34506E F C第5题图在xy 150=中,令10=y , 得15=x . 所以自变量的取值范围为15≥x . ⑵在x y 150=中,令2=y , 得75=x . 所以当75≥x 时, 2≤y .所以,从消毒开始, 至少在75分钟的时间内, 师生不能进入教室.。