下载文档原格式
课题因式分解十字相乘法1、认识因式分解的意义。
教课目的2、娴熟运用适合的方法进行因式分解。
要点：因式分解的观点以及运用提取公因式法和公式法分解因式。
要点、难点难点：运用因式分解进行多项式的除法以及解简单的一元二次方程。
教课内容一、概括定义：把一个多项式化为几个整式的积的形式，这类变形叫做把这个多项式因式分解，也叫作分解因式。
意义：它是中学数学中最重要的恒等变形之一，它被宽泛地应用于初等数学之中，是我们解决很多半学问题的有力工具。
因式分解方法灵巧，技巧性强，学习这些方法与技巧，不单是掌握因式分解内容所必要的，并且对于培育学生的解题技术，发展学生的思想能力，都有着十分独到的作用。
学习它，既能够复习的整式四则运算，又为学习分式打好基础；学好它，既能够培育学生的察看、注意、运算能力，又能够提升学生综合剖析和解决问题的能力。
分解因式与整式乘法互为逆变形。
二、因式分解的方法因式分解没有广泛的方法，初中数学教材中主要介绍了提公因式法、公式法。
而在比赛上，又有拆项和添减项法，分组分解法和十字相乘法，待定系数法，双十字相乘法，对称多项式轮换对称多项式法，余数定理法，求根公式法，换元法，长除法，除法等。
注意三原则1分解要完全2最后结果只有小括号3 最后结果中多项式首项系数为正（比如：-3 x2+x=-x(3x-1)）十字相乘法分解因式1．二次三项式（ 1）多项式ax2bx c ，称为字母的二次三项式，此中称为二次项，为一次项，为常数项．比如： x22x 3 和 x25x 6 都是对于x的二次三项式．（ 2）在多项式x26xy 8y2中，假如把看作常数，就是对于的二次三项式；假如把看作常数，就是对于的二次三项式．（ 3）在多项式2a2b27ab3中，把看作一个整体，即，就是对于的二次三项式．同样，多项式 (x ) 27()12，把看作一个整体，就是对于的二次三项式．y x y2．十字相乘法的依照和详细内容(1) 对于二次项系数为 1 的二次三项式x2(a b)x ab (x a)(x b)方法的特点是“拆常数项，凑一次项”当常数项为正数时，把它分解为两个同号因数的积，因式的符号与一次项系数的符号同样；当常数项为负数时，把它分解为两个异号因数的积，此中绝对值较大的因数的符号与一次项系数的符号同样．(2) 对于二次项系数不是 1 的二次三项式ax 2bx c a1 a2 x2( a1c2a2c1 ) x c1c2(a1x c1 )(a2 x c2 )它的特点是“ 拆两端，凑中间”当二次项系数为负数时，先提出负号，使二次项系数为正数，而后再看常数项；常数项为正数时，应分解为两同号因数，它们的符号与一次项系数的符号同样；常数项为负数时，应将它分解为两异号因数，使十字连线上两数之积绝对值较大的一组与一次项系数的符号同样注意：用十字相乘法分解因式，还要注意防止以下两种错误出现：一是没有仔细地考证交错相乘的两个积的和能否等于一次项系数；二是由十字相乘写出的因式漏写字母．二、典型例题例 1把以下各式分解因式：(1) x22x 15 ；(2) x25xy 6y 2．例 2把以下各式分解因式：(1) 2x25x 3；(2) 3x28x 3 ．例 3把以下各式分解因式：1）x410x29 ；(2) 7( x y) 35( x y) 22( x y) ；(3) ( a28a) 222(a28a)120 ．例 4分解因式：(x22x 3)( x22x 24)90 ．例 5分解因式6x45x338 x25x6．例 6分解因式x22xy y25x 5y 6．例 7 分解因式： ca(c－a)＋bc(b－c)＋ab(a－ b)．试一试：把以下各式分解因式：(1) 2x215x 7(2)3a28a 4(3)5x27x 6(4) 6 y211y 10 (5)5a2b223ab 10(6)3a2 b217abxy 10 x2 y2(7)x27xy12 y2 (8)x47x218(9)4m28mn 3n2(10)5x515x3 y20xy2课后练习一、选择题1．假如x2px q( x a)( x b)，那么p 等于()A ． ab B． a＋ b C．－ ab D ．－ (a＋ b)2．假如x2(a b) x 5b x2x 30 ，则b为( )A ． 5B．－ 6C．－ 5 D ． 63．多项式x23x a 可分解为(x－5)(x－b)，则a，b的值分别为( ) A．10和－2B．－10和2C．10 和 2D．－10 和－ 24．不可以用十字相乘法分解的是()A ．x2x2B ．3x210x23x C． 4x 2x 2D．5x26xy 8y2 5．分解结果等于 (x＋ y－ 4)(2x＋ 2y－ 5)的多项式是()A ．2( x y)213(x y)20B．( 2x 2 y)213(x y)20C．2( x y)213( x y)20D．2( x y) 29( x y)206．将下述多项式分解后，有同样因式x－1 的多项式有()① x27x 6 ；② 3x22x 1 ；③ x 25x 6 ；④ 4x25x9；⑤ 15x223x 8；⑥ x 411x212A．2个B．3 个C．4 个D．5 个二、填空题7．x23x 10 8．m25m6__________．(m＋ a)(m＋b)． a＝ __________，b＝ __________ ．9．2x25x 3(x－ 3)(__________) ．10． x2____2y2(x－ y)(__________) ．11．a2n a(_____)(________) 2．m12．当 k＝ ______时，多项式3x27x k 有一个因式为(__________)．13．若 x－ y＝ 6，xy17，则代数式 x3 y2x2 y2xy3的值为__________．36三、解答题14．把以下各式分解因式：(1) x47x2 6 ；(2) x45x236 ；(3) 4x465x 2 y 216 y 4；(4) a67a3b38b6；(5) 6a45a34a2；(6) 4a637a4 b29a2 b4．15．把以下各式分解因式：(1) ( x23)24x2；(2) x2( x 2)29 ；(3) (3x22x 1)2(2x 23x 3)2；(4) ( x2x)217( x2x) 60 ；(5) ( x22x) 27( x22x) 8 ；．16．已知 x＋ y＝ 2， xy＝ a＋4，x3y326 ，求a的值．。
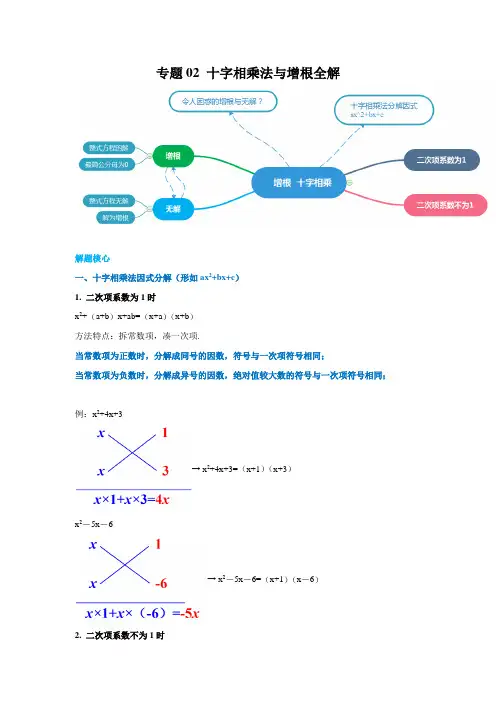
专题02 十字相乘法与增根全解解题核心一、十字相乘法因式分解（形如ax2+bx+c）1. 二次项系数为1时x2+（a+b）x+ab=（x+a）（x+b）方法特点：拆常数项，凑一次项.当常数项为正数时，分解成同号的因数，符号与一次项符号相同；当常数项为负数时，分解成异号的因数，绝对值较大数的符号与一次项符号相同；例：x2+4x+3→ x2+4x+3=（x+1）（x+3）x2－5x－6→ x2－5x－6=（x+1）（x－6）2. 二次项系数不为1时ax2+bx+c=a1a2x2+（a1c2+a2c1）x+c1c2=（a1x+c1）（a2x+c2）此类特点：拆两头，凑中间1. 当二次项系数为负数时，提取符号，将其转变为正数2. 二次项系数只分解成两个正数的乘积3. 常数项分解参考上一类4. 分解后横向写结果.例：2x2－3x－5→ 2x2－3x－5=（x+1）（2x－5）3. 多字母例：4x2－3xy－y2→ 4x2－3xy－y2=（x－y）（4x+y）二、分式方程的增根与无解1. 增根意义：（1）增根是所给分式方程去分母后整式方程的根；（2）（1）中的根使分式方程分母为0.2. 分式方程无解与增根无解：分式方程化成整式方程后，（1）整式方程无解；（2）整式方程的所有的解均为增根. 增根：①是分式方程转化为整式方程后的解；②该解使得原分式方程分母为0.*分式方程无解≠分式方程有增根；分式方程有增根≠分式方程无解.若分式方程无解，且分式方程转化整式方程后有解，则该解必为增根.释义：1. 分式方程10x= 去分母得：1=0×x ，此方程无解； 2. 分式方程20x x= 去分母得：x 2=0，解得x=0，此时分母为0，无意义，故x=0是分式方程的增根，此方程无解；3. 分式方程()10x x x-= 去分母得：x （x －1）=0，解得x=0或x=1，x=0是分式方程的增根，分式方程的解为x=1. 4. 若分式方程21x m x -=+无解，求m 值. 去分母得：x －m=2x+2，x=－m －2，原方程无解，则x=－1，即－m －2=－1，m=－1.5. 若分式方程21x m x -=+m 无解，求m 值. 去分母得：x －m=2mx+2m ，(1-2m)x=3m ，因为原方程无解，则：1-2m=0或3112m m=--，即m=0.5或m=-1.★解分式方程时一定要“检验”！【题型一】十字相乘【例1－1】（1）x 2+14x+24；（2）a 2－15a+36；（3）x 2+4x －5【答案】（1）原式= (x+2)(x+12)（2）原式= (a-3)(a-12)（3）原式= (x+5)(x-1)【例1－2】（1）x2+x－2；（2）y2－2y－15；（3）x2－10x－24【答案】（1）原式= (x+2)(x-1) （2）原式= (y-5)(y+3) （3）原式= (x-12)(x+2)【例1－3】（1）5x2+7x－6；（2）3x2－7x+2；（3）10x2－17x+3；（4）－6t2+11t+10【答案】（1）原式= (x+2)(5x-3) （2）原式= (x-2)(3x-1) （3）原式=-(2t-5)(3t+2)【例2－1】（1）x2-3xy+2y2；（2）m2-6mn+8n2；（3）a2-ab-6b2【答案】（1）原式= (x-2y)(x-y) （2）原式= (m-2n)(m-4n) （3）原式= (a-3b)(a+2b)【例2－2】（1）15x2+7xy-4y2；（2）12x2-11xy-15y2【答案】（1）原式= (3x-1)(5x+4)（2）原式= (3x-5)(4x+3)【例3－1】（1）（x+y）2-3（x+y）-10；（2）（a+b）2-4a-4b+3（3）12（x+y）2+11（x2-y2）+2（x-y）2【答案】（1）原式=（x+y-5）（x+y+2）（2）原式=（a+b）2-4（a+b）+3=（a+b-1）（a+b-3）（3）原式=12（x+y）2+11（x+y）（x-y）+2（x-y）2 =（3x+3y+2x-2y）（4x+4y+x-y）=（5x+y）（5x+3y）【例3－2】（1）（x2-3）2-4x2；（2）（x2+x）2-17（x2+x）+60（3）（x2+2x-3）（x2+2x-24）+90【答案】（1）原式=（x2-3+2x）（x2-3－2x）=（x+3）（x-1）（x-3）（x+1）（2）原式=（x2+x-12）（x2+x-5）=（x+4）（x-3）（x2+x-5）（3）令x2+2x=t，原式=（t-3）（t-24）+90=t2-27t+162=（t-9）（t-18）=（x 2+2x-9）（x 2+2x-18）【例4－1】（2020·长沙市月考）如果关于x 的不等式组213272x x x a+⎧-≤⎪⎨⎪<-⎩有且仅有2个整数解，并且关于y 的分式方程45333y a a y y++=--有整数解，则符合条件的所有整数a 的和是（ ） A ．24B ．15C ．12D ．7【答案】C. 【解析】解：213272x x x a +⎧-≤⎪⎨⎪<-⎩①②解①得：x≥−2，解②得：x ＜27a -， 不等式组的解集为−2≤x ＜27a -， 因为不等式组有且仅有2个整数解，所以−1＜27a -≤0． 解得2≤a ＜9分式方程去分母得：y ＋4a−5a ＝3（y−3），解得：y ＝92a -． 经检验：a ＝5或7是分式方程的解．则所有整数a 的和为12．故答案为：C ．【例4－2】（2020·重庆月考）若关于x 的分式方程4222a x x-=--的解为正整数，且关于y 的不等式组25220y y y a -⎧+<⎪⎨⎪-≤⎩无解，则满足条件的所有整数a 的值之和是（ ）A ．18-B ．14-C ．10-D ．6-【答案】D.【解析】解不等式组，y>83，y≤a∵不等式组无解，∴a≤83，分式方程去分母得，4+a=2x-4，解得，x=82a+，∵分式的解为正整数，∴82a+>且822a+≠，∴883a-<≤且4a≠-∴整数a=-6，-2，0，2，∴整数a之和为：-6．故答案为：D．【例4－3】（2020·重庆月考）若关于x的一元一次不等式组12(35)334333x axx⎧--≤⎪⎪⎨+⎪>+⎪⎩无解，且关于y的分式方程223211y a yy y---=--有非负整数解，则符合条件的所有整数a的和为（）A．7 B．8 C．14 D．15 【答案】C.【解析】解：解不等式组12(35)334333x axx⎧--⎪⎪⎨+⎪>+⎪⎩，得16x ax-⎧⎨>⎩，∵不等式组12(35)334333x axx⎧--⎪⎪⎨+⎪>+⎪⎩无解，∴a-1≤6，即a≤7，解分式方程，得y=12a+，为非负整数，且a≤7，∴a=-1或1或3或5或7，a=1时，y=1，原分式方程无解，a=1舍去，符合条件的所有整数a 的和是14，故答案为：C ．【例5－1】（2020·河北石家庄市期中）若关于x 的分式方程3mx x -－2＝23m x -无解，则m 的值为（ ）A ．0B ．2C ．0或2D ．无法确定 【答案】C.【解析】解：分式方程去分母，得：（m-2）x=2m-6，由分式方程无解，①m-2=0，m=2，②x −3=0，即x =3，把x =3代入整式方程得：m =0，故答案为：C ．【例5－2】（2020·长沙市月考）请你利用我们学习的“分式方程及其解法”解决下列问题： （1）已知关于x 的方程2112mx x -=+的解为负数，求m 的取值范围； （2）若关于x 的分式方程322133x nx x x --+=---无解．求n 的取值范围． 【答案】见解析．【解析】解：（1）去分母，得2mx-1=x+2，当2m-1≠0时，解得：x=321m -， ∵ 方程有解，且解为负数， ∴2103221m m -<⎧⎪⎨≠-⎪-⎩，解得m ＜12且m≠14-； （2）分式方程去分母整理得：（n-1）x=2，当n －1=0时，方程无解，此时n =1；当n-1≠0时，x=21n -， 要使方程无解，则21n -=3，解得：n=53； 综上，n=53或n =1．【例5－3】（2020·湖南株洲市期中）若分式方程144-=--x m x x 无解，则m =__________． 【答案】3.【解析】解：方程去分母得：m ＝x ﹣1，解得：x ＝m +1，∴当x ＝4时分母为0，方程无解，即m +1＝4，∴m ＝3时方程无解．故答案为：3. 【例5－4】（2020·新乐市月考）若关于x 的分式方程223111m x x x -=+--无解，则m =________． 【答案】32-或2. 【解析】解：去分母可得：（m-2）x=m+5，当m-2=0时，∴ m=2，此时方程无解，满足题意，当m-2≠0时，x=52m m +-， 由于该分式方程无解，x 2-1=0，x=1或x=-1 即52m m +-=-1或1， 解得：m=32-， 故答案为：32-或2． 【例5－5】（2020·黑龙江齐齐哈尔市期末）如果方程322x m x x -=-- 无解，则m=___________． 【答案】1.【解析】解：去分母，得x －3=﹣m ，∵原方程无解，∴x －2=0，即x =2，把x =2代入上式，得2－3=﹣m ，所以m =1．故答案为1．【例6－1】（2020·四川省成都期中）关于x 的分式方程3601(1)x k x x x x ++-=--有解，则k 该满足什么条件？【答案】见解析.【解析】解：原方程整理得：8x=k+3∵该分式方程有解，∴x≠0，且x≠1，即k+3≠0且k+3≠8，解得：k≠-3且k≠5．【例6－2】（2020·北京师大附中期中）当k 为何值时，关于x 的方程123(2)(3)x x x k x x x x ++-=-+-+的解为负数. 【答案】见解析.【解析】解：分式方程解得：x=35k -， ∵方程的解为负数，且使得分式有意义， ∴305325335k k k -⎧<⎪⎪-⎪≠⎨⎪⎪-≠-⎪⎩， 解得k ＜3且k≠-12．【例6－3】（2020·黑龙江绥化市模考）关于x 的分式方程2111x a x x -=+-的解为负数，则a 的取值范围____．【答案】见解析.【解析】解：原方程化为：x=1-a ，∵分式方程的解为负数，∴1-a ＜0，∴a>1∵x≠1，且x≠-1，∴1-a≠-1，得a≠2故答案为：a ＞1且a≠2．【例6－4】（2020·长沙市月考）已知关于x的分式方程2311x kx x-=--的解为正数，则k的取值范围为________．【答案】k<32且k≠12.【解析】解：去分母得，x-3（x-1）=2k解得：x=322k -，∵分式方程的解为正数，∴322k->，且3212k-≠解得，k<32且k≠12故答案为：k<32且k≠12．【例7－1】（2020·山东济南市期中）若关于x的方程12x-+3＝12axx--有增根，则a＝_____．【答案】1.【解析】解：去分母，得1+3x﹣6＝ax﹣1，∵方程有增根，所以x﹣2＝0，x＝2是方程的增根，将x＝2代入上式，得1+6﹣6＝2a﹣1，解得a＝1，故答案为1．【例7－2】（2020·昌乐县期中）若关于x的分式方程4333x ax x--=--有增根，则a的值是______．【答案】－1.【解析】解：原分式方程解得：x=52a -∵分式方程有增根，∴52a-=3，解得a=-1．故答案为：-1．【例7－3】（2020·浙江杭州市模拟）关于x的方程32211x mx x--=++有增根，则m的值为___．【答案】-5.【解析】解：分式方程解得：x=m+4，因为分式方程由增根，即x=-1∴m+4=-1即m=-5故答案为-5.【例7－4】（2020·四川成都市期中）已知关于x 的分式方程222242mx x x x +=--+．若方程有增根，则m 的值为_______．【答案】±4. 【解析】解：分式方程变为：mx=-8，由方程有增根，得x=2或x=-2∴m=-4或m=4故答案为：±4. 【例7－4】（2020·浙江杭州市模拟）关于x 的方程213242ax x x x +=--+有增根，则a 的值为_______．【答案】-2或6.【解析】解：方程整理得：（2-a ）x=8，∵原方程有增根，∴x=2或x=-2∴a=-2或a=6故答案为：-2或6．【例7－5】（2020·湖南岳阳市期中）若关于x 的分式方程355x a x x -=--有增根，则a 的值为__________．【答案】5.【解析】解：原方程两边同时乘以（x-5）得：x-3（x-5）=a，由题意，x=5，∴a=5，故答案为5 ．。
因式分解-十字相乘法一、十字相乘法分解因式十字相乘法：有些二次三项式，可以把第一项和第三项的系数分别分解为两个数之积，然后借助画十字交叉线的方法，把二次三项式进行因式分解，这种方法叫十字相乘法。
简单的说十字相乘法就是：十字左边相乘等于二次项系数，右边相乘等于常数项，交叉相乘再相加等于一次项系数。
注意：十字相乘法不是适合所有二次三项式，只有在一次项系数和二次项系数以及常数项存在一种特殊关系时才能用，这个特殊关系我们通过例题来说明：1、首项系数是1的二次三项式的因式分解，我们学习了多项式的乘法，即()()()x a x b x a b x ab ++=+++2将上式反过来，()()()x a b x ab x a x b 2+++=++得到了因式分解的一种方法——十字相乘法，用这种方法来分解因式的关键在于确定上式中的a 和b ，例如，为了分解因式x px q 2++，就需要找到满足下列条件的a 、b ；a b pab q +==⎧⎨⎩如把762-+x x 分解因式，首先要把二次项系数2x 分成x x ⨯，常数项-7分成)1(7-⨯，写成十字相乘，左边两个数的积为二次项，右边两个数的积为常数项。
交叉相乘的和为x x x 67)1(=⨯+-⨯，正好是一次项。
从而)1)(7(762-+=-+x x x x 。
2、二次项系数不为1的二次三项式的因式分解二次三项式ax bx c 2++中，当a ≠1时，如何用十字相乘法分解呢？分解思路可归纳为“分两头，凑中间”，例如，分解因式2762x x -+，首先要把二次项系数2分成1×2，常数项6分成()()-⨯-23，写成十字相乘，左边两个数的积为二次项系数。
右边两个数相乘为常数项，交叉相乘的和为()()13227⨯-+⨯-=-，正好是一次项系x =-+762x )1)(7(-+x x xx⇓⨯⇓71-xx x 67=+-数，从而得()()2762232x x x x -+=--。
十字相乘法分解因式一、学习目标 1、能记住十字相乘法2、会运用十字相乘法分解因式（重点） 二、知识复习1．二次三项式（1）多项式c bx ax ++2，称为字母 的二次三项式，其中 称为二次项， 为一次项， 为常数项．例如：322--x x 和652++x x 都是关于x 的二次三项式．（2）在多项式2286y xy x +-中，如果把 看作常数，就是关于 的二次三项式；如果把 看作常数，就是关于 的二次三项式．（3）在多项式37222+-ab b a 中，把 看作一个整体，即 ，就是关于- 的二次三项式．同样，多项式12)(7)(2++++y x y x ，把 看作一个整体，就是关于 的二次三项式． 2．十字相乘法的依据和具体内容(1)对于二次项系数为1的二次三项式))(()(2b x a x ab x b a x ++=+++ 方法的特征是“拆常数项，凑一次项”当常数项为正数时，把它分解为两个同号因数的积，因式的符号与一次项系数的符号相同； 当常数项为负数时，把它分解为两个异号因数的积，其中绝对值较大的因数的符号与一次项系数的符号相同． (2)对于二次项系数不是1的二次三项式c bx ax ++2))(()(2211211221221c x a c x a c c x c a c a x a a ++=+++=它的特征是“拆两头，凑中间”当二次项系数为负数时，先提出负号，使二次项系数为正数，然后再看常数项； 常数项为正数时，应分解为两同号因数，它们的符号与一次项系数的符号相同； 常数项为负数时，应将它分解为两异号因数，使十字连线上两数之积绝对值较大的一组与一次项系数的符号相同注意：用十字相乘法分解因式，还要注意避免以下两种错误出现：一是没有认真地验证交叉相乘的两个积的和是否等于一次项系数；二是由十字相乘写出的因式漏写字母． 三、典型例题[例1] 把下列各式因式分解。
（1）3722+-x x （2）5762--x x （3）22865y xy x -+解：（1）)12)(3(3722--=+-x x x x1231--7)1(1)3(2-=-⨯+-⨯（2）)53)(12(5762-+=--x x x x5312-713)5(2-=⨯+-⨯（3）)45)(2(86522y x y x y xy x -+=-+yy4521-y y y 6)2(5)4(1=⨯+-⨯ 四、当堂检测1、把下列各式分解因式：（1）22157x x ++ （2） 2384a a -+- （3） 2576x x +- （4）261110y y -- （5）1032+--x x （6）652--m m二、分解因式1. 2252310a b ab +- 2. 222231710a b abxy x y -+ 3. 22712x xy y -+ 4.42718x x +- 5.22483m mn n ++。
[文件] sxc2dja0016.doc[科目] 数学[年级] 初二[章节][关键词] 十字相乘/二次齐次式/换元法/因式分解[标题] 十字相乘(2)[内容]十字相乘(2)教学目标1.使学生掌握通过换元的方法，把可以转化为形如x2+px+q的某些多项式分解因式，渗透化归和整体思想方法；2.掌握某些二次齐次式的因式分解方法.教学重点和难点重点：运用换元法，对可转化为形如x2+px+q的某些多项式进行因式分解.难点：理解二次三项式x2+px+q中的x即可以是单项式，也可以是多项式；对于p和q，不仅可以是单项式(包括数)，也可以是多项式.教学过程设计一、复习1.把下列各式分解因式：(1)x2+5x+4；(2)y2+4y－5；(3)m2－6m+8；(4)p2－5p－36.答：(1)(x+1)(x+4)； (2)(y+5)(y－1)；(3)(m－2)(m－4)； (4)(p+4)(p－9).2.问：在二次三项式x2+px+q中，p和q各满足什么条件时，可以因式分解?答：把常数q分解因数，选择其中的两个因数，使它们的代数和等于p，此时，二次三项式x2+px+q可以分解因式.二、新课二次三项式x2+px+q中的x，不仅可以是单项式，也可以是多项式. 同样，P和q不仅可以是单项式(包括数)，也可以是多项式.对于这样的多项式怎样分解因式呢?例1 把x4+6x2+8分解因式.分析：这个多项式不是关于x的二次三项式，如果把x2设为y，那么这个多项式就可转化为y2+6y+8，这是关于y的二次三项式，我们就可以运用上一节课所学的方法分解因式了.这里，设y=x2，把y称为辅助元，这种方法叫做换元法解设x2=y，则多项式变为y2+6y+8，把它分解因式，得y2+6y+8=(y+2)(y+4).再把y换成x2，得x4+6x2+8=(x2) 2+6x2+8=(x2+2)(x2+4).指出：通过设辅助元，把所给的多项式转化为形如x2+px+q的二次三项式，在解题中，代换的步骤可以省略.例2 把(a+b) 2－4(a+b)+3分解因式.分析：如果把(a+b)看作一个整体，这样原多项式可看成关于(a+b)的二次三项式，就可以进行因式分解了.解 (a+b) 2－4(a+b)+3=(a+b－1)(a+b－3).指出：把(a+b)看作二次三项式x2+px+q中的字母x的方法称为“换元法”，这种“整体”思想方法是代数中的主要思想方法，它能起到化难为易，化繁为简的作用.例3 把(x2－3x+2)(x2－3x－4)－72因式分解.分析：这个多项式较复杂，若能注意题目中的各项的特点，把某些项看作一个整体，运用代换法，即通过设辅助元，把原多项式转化为形如x2+px+q的二次三项式，就可以进行因式分解了.问：运用整体思想和换元法，可以有几种不同的分解因式的方法?(不要求写出设辅助元的代换过程.)解方法1 把x2－3x看作一个整体.原式=[(x2－3x)+2][(x2－3x)－4]－72=(x2－3x)2－2(x2－3x)－80=(x2－3x－10)(x2－3x+8)=(x－5)(x+2)(x2－3x+8).方法2 把x2－3x+2看作一个整体.原式=(x2－3x+2)[(x2－3x+2)－6]－72=(x2－3x+2)2－6(x2－3x+2)－72=[(x2－3x+2)－12][(x2－3x+2)+6]=(x2－3x－10)(x2－3x+8)=(x－5)(x+2)(x2－3x+8).方法3 把x2－3x－4看作一个整体.原式=[(x2－3x－4)+6](x2－3x－4)－72=(x2－3x－4)2+6(x2－3x－4)－72=(x2－3x－4+12)(x2－3x－4－6)=（x2-3x+8）(x2-3x-10)=(x2－3x+8)(x－5)(x+2).指出；通过例3可以看到，如果把二次三项式(x2－3x+2)与二次三项式(x2－3x－4)相乘，将得到一个四次多项式，这时再分解因式就困难了.如果把其中的某些项看作一个整体(即把它看作一个新的辅助元)，这就把问题转化为我们熟悉的关于新辅助元的二次三项式，就可以用学过的方法分解因式了.例4 把x2－3xy+2y2分解因式.问：所给的多项式的结构特点是什么?答：多项式中的x和y的最高次项都是2次，中间项x与y的乘积项，次数也是2次，因此这个多项式既可以看作是关于x的二次三项式，也可以看作是关于y的二次三项式.问：如果把它看作是关于x的二次三项式，怎样分解因式?答：这时，2y2就相当于常数项，可以把它分解为－y与－2y的积，那么－y+(－2y)=－3y恰好等于一次项x的系数.解 x2－3xy+2y2=x2－3yx+2y2=(x－y)(x－2y).指出：由例4可以看到，当二次三项式x2+px+q中的p和q是一个单项式时，如果q可以分觖成两个因式之积，而这两个因式之和正好等于一次项系数p时，这样的二次三项式就可以分解因式.三、课堂练习把下列各式分解因式：1.x4－15x2+26；2.(x+y) 2－(x+y)－2；3.y4－26y2+25；4.(a－b) 2+6(b－a)+5；5.(x2－2x)2－7(x2－2x)－8；6.x2－2xy－8y2；7.x2+(a+b)x+ab； 8.x4－7x2y2+6y4；9.(a+b) 2+m(a+b)－12m2.答案：1.(x2－13)（x2-2）；2.(x+y+1)(x+y－2)；3.(y+5)(y－5)(y+1)(y－1)；4.(a－b－1)(a－b－5)；5.(x－4)(x+2)(x－1) 2；6.(x+2y)(x－4y)；7.(x+a)(x+b)； 8.(x+y)(x－y)(x2－6y2)；9.(a+b+4m)(a+b－3m).四、小结本节课所讨论的四个例题都可以通过换元方法，即整体思想方法把原问题转化为形如x2+px+q的二次三项式的因式分解问题.学会具体解题方法固然重要，但通过解数学题掌握数学思想方法更为重要.五、作业把下列各式分解因式：1.(1)x4+7x2－18；(2)x6+8x3+15；(3)m2x2－8mx+12；(4)x2y2－7xy+10；2.(1)x2－7xy+12y2；(2)a2+2ab－15b2；(3)m2+4mn－12n2；(4)p2+9pq+18q2.3.(1)(m+n) 2－(m+n)－30；(2)(x－y) 2－3(x－y)－40；(3)(2m+n) 2－4r(2m+n)+3r2； (4)(a－b) 2－12(a－b)－45.4.(1)(x2－4x) 2－(x2－4x)－20；(2)(a2+5a+3)(a2+5a－2)－6.答案：1.(1)(x2－2)(x2+9)；(2)(x2+3)(x3+5)；(3)(mx－2)(mx－6)；(4)(xy－2)(xy－5).2.(1)(x－3y)(x－4y)；(2)(a+5b)(a－3b)；(3)(m－2n)(m+6n)；(4)(p+3q)(p+6q).3.(1)(m+n－6)(m+n+5)；(2)(x－y+5)(x－y－8)；(3)(2m+n－r)(2m+n－3r)； (4)(a－b－15)(a－b+3).4.(1)(x+1)(x－5)(x－2) 2；(2) (a2+5a+3)(a2+5a－4)－6=[(a2+5a)+3][(a2+5a)－2]－6=(a2+5a) 2+(a2+5a)－12=(a2+5a+4)(a2+5a－3)=(a+1)(a+4))(a2+5a－3).课堂教学设计说明通过例1～例3的讨论，向学生介绍换元法，渗透整体思想和化归的思想方法，关于换元法和整体思想方法，在教科书中没有向学生提出，但是，对于帮助学生理解和掌握如例1～例3类型的问题，让学生学习换元法和整体思想方法是有重要作用的.通过换元法把可化归为形如x2+px+q的某些多项式分解因式，使学生体会到，学习新知就说好比“上楼梯”，要逐步登级而上；但是在解决新问题时，常常是通过某种方法和手段，把未知的知识化归为用已知的知识去解决，这就好比“下楼梯”，由高往低，逐级而下“上楼梯”与“下楼梯”的关系可以形象地说明在数学中解决问题的主要思想方法.在教学中，通过例题的讨论，引导学生学会在解数学题时，从整体上观察、思考和处理问题，这不仅是一种重要的数学方法，而且是解决有关数学问题时常用的一种技能和技巧.。
十字相乘法分解因式(1)对于二次项系数为1方法的特征是“拆常数项，凑一次项”当常数项为正数时，把它分解为两个同号因数的积，因式的符号与一次项系数的符号相同；当常数项为负数时，把它分解为两个异号因数的积，其中绝对值较大的因数的符号与一次项系数的符号相同．(2)对于二次项系数不是1的二次三项式它的特征是“拆两头，凑中间”当二次项系数为负数时，先提出负号，使二次项系数为正数，然后再看常数项；常数项为正数时，应分解为两同号因数，它们的符号与一次项系数的符号相同；常数项为负数时，应将它分解为两异号因数，使十字连线上两数之积绝对值较大的一组与一次项系数的符号相同注意：用十字相乘法分解因式，还要注意避免以下两种错误出现：一是没有认真地验证交叉相乘的两个积的和是否等于一次项系数；二是由十字相乘写出的因式漏写字母．例5、分解因式：652++x x分析：将6分成两个数相乘，且这两个数的和要等于5。
由于6=2×3=(-2)×(-3)=1×6=(-1)×(-6)，从中可以发现只有2×3的分解适合，即2+3=5。
1 2解：652++x x =32)32(2⨯+++x x 1 3 =)3)(2(++x x 1×2+1×3=5用此方法进行分解的关键：将常数项分解成两个因数的积，且这两个因数的代数和要等于一次项的系数。
例1、分解因式：672+-x x解：原式=)6)(1()]6()1[(2--+-+-+x x 1 -1=)6)(1(--x x 1 -6（-1）+（-6）= -7练习1、分解因式(1)24142++x x (2)36152+-a a (3)542-+x x练习2、分解因式(1)22-+x x (2)1522--y y (3)24102--x x（二）二次项系数不为1的二次三项式—— c bx ax ++2条件：（1）21a a a = 1a 1c （2）21c c c = 2a 2c（3）1221c a c a b += 1221c a c a b +=分解结果：c bx ax ++2=))((2211c x a c x a ++例2、分解因式：101132+-x x分析： 1 -2（-6）+（-5）= -11解：101132+-x x =)53)(2(--x x练习3、分解因式：（1）6752-+x x （2）2732+-x x（3）317102+-x x （4）101162++-y y（三）多字母的二次多项式例3、分解因式：221288b ab a --分析：将b 看成常数，把原多项式看成关于a 的二次三项式，利用十字相乘法进行分解。
初中数学十字相乘法因式分解要点：一、 x 2 ( p q) xpq 型的因式分解特点是：（ 1）二次项的系数是 1（2）常数项是两个数之积（ 3）一次项系数是常数的两个因数之和。
对这个式子先去括号，获取：x 2( p q)x pqx 2 px qx pq(x 2 px) (qxpq)x( x p) q(x p) (x p)( x q)因此： x 2 ( p q)x pq (x p)( x q)利用此式的结果能够直接将某些二次项系数是 1 的二次三项式分解因式。
二、一般二次三项式 ax 2 bx c 的分解因式大家知道， (a x c )(a x c 2 ) a a x 2 (a c a c 1 ) x c c 。
11 21 2 1 2 21 2反过来，即可获取： a 1a 2 x 2 (a 1c 2 a 2 c 1 ) x c 1c 2(a 1 x c 1 )(a 2 x c 2 )我们发现，二次项系数a 分解成 a 1 a 2 ，常数项 c 分解成 c 1 c 2 ，把 a 1, a 2 , c 1, c 2 写成a 1 c1 ，这里按斜线交织相乘，再相加，就获取a 1c 2 a 2 c 1 ，那么 ax 2bx c 就可以分a 2 c 2解成 (a 1 x c 1 )(a 2 x c 2 ) .这种借助画十字交织线分解系数， 从而将二次三项式分解因式的方法， 叫做十字相 乘法。
【典型例题】 [ 例 1] 把以下各式分解因式。
（ 1） x 2 3x 2（2） x 2 7x 6 ，这解析：（1）x 23 x 2的二次项的系数是，常数项21 2 ，一次项系数 3 1 2 是一个 x 21( p 7 q) x pq 型式子。
（2） x 2 x 6 的二次项系数是 ，常数项6 ( 1) ( 6) ，一次项系数7 ( 1)1( 6) ，这也是一个 x 2 ( p q)xpq 型式子，因此可用公式 x 2 ( p q) x pq ( xp)( x q) 分解以上两式。
因式分解中的十字相乘法《因式分解中的十字相乘法》嘿，你知道吗？在数学这个神奇的世界里，有一个特别有趣又超级有用的方法，那就是十字相乘法。
我呀，今天就想和你唠唠这个十字相乘法。
我先给你举个简单的例子吧。
就像有个二次三项式，比如说x²+5x + 6。
这时候十字相乘法就像一个超级侦探，来把它分解因式啦。
我们要把二次项系数和常数项分别拆成两个数相乘呢。
对于x²的系数1，那就是1×1啦。
对于常数项6呢，我们可以拆成2×3。
然后我们就像搭十字一样，把这些数字摆好。
1和2写在一边，1和3写在另一边，交叉相乘再相加，1×3 + 1×2刚好等于一次项系数5呢。
这样，这个式子就可以分解成(x + 2)(x+ 3)啦。
哇，是不是很神奇呢？我记得我刚开始学这个十字相乘法的时候，那可真是一头雾水啊。
我就想，这都是啥呀，为啥要这么拆数字呢？我就跑去问我的数学老师。
老师就笑着说：“你看啊，这就像是搭积木，每一块积木都有它合适的位置。
二次三项式就像一个待组装的大积木，你得找到合适的小积木块才能把它搭好呀。
”我当时似懂非懂的，不过老师这么一说，我就觉得好像这个方法也没那么难嘛。
有一次，我和我的同桌一起做数学作业。
碰到了一个比较难的二次三项式，好像是2x² - 7x + 3。
我就开始苦思冥想，按照十字相乘法的规则来拆数字。
我先把2x²拆成2x 和x，对于常数项3呢，我拆成- 1和- 3。
我试着搭十字，交叉相乘再相加，结果不对呢。
我就有点沮丧，哎呀，这可怎么办呀。
这时候我的同桌凑过来说：“你看，你把3拆成- 1和- 3不对呢。
你可以把2x²拆成2x和x不变，把3拆成- 1和- 3的话，那交叉相乘再相加就不是- 7x啦。
你应该把3拆成- 1和- 3，2x乘以- 1加上x乘以- 3就等于- 7x啦。
”我一听，眼睛一亮，原来是这样啊。
我就按照同桌说的方法做，果然就把这个式子分解成(2x - 1)(x - 3)啦。
