下载文档原格式
第一讲等差数列基础关于第一讲等差数列，是中年级学习的一个重点。
高年级的很多题虽不是直接考察等差数列，但往往中间的某一步需要用到等差数列的知识。
等差数列这讲公式繁多，但希望孩子们千万不要死记硬背这些公式，一定要理解着记忆。
死记硬背公式不易记牢，往往容易出错，考试中一旦出现，背错公式，分数就得不到了；在在我总结的知识点解析里每个公式，我都讲了理解的方法。
可以在做题时反复理解几次，就不容易出错了。
关于计算这里，再啰嗦几句。
很多孩子的计算基本功不过关，所以往往上课时算式列出来了，但不会算，算得慢或算不准，这样就太可惜了。
所以希望孩子们能够每天坚持练几道大数乘除法。
乘法可以按照三位数×一位数，两位数×两位数，三位数×两位数，四位数×两位数，三位数×三位数，四位数×三位数。
除法可以从三位数÷一位数，四位数÷一位数，三位数÷两位数，四位数÷一位数，五位数÷一位数，五位数÷三位数等等这样的顺序练起。
一、通项公式知识点解析：⒈第n项=首项+（n-1）×公差理解方法：可以对比植树问题来理解等差数列，第二项比第一项多一个公差，第三项比第一项多两个公差，……第n项比第一项多（n-1）个公差。
辅助练习：等差数列5、8、11……求这个数列的第2011项是多少？答：5+（2011-1）×3=6035这个公式含有四个量首项，第n项，项数n，公差，这四个其实是知三求一的。
⒉首项=第n项-（n-1）×公差理解方法：同1，第n项比第一项多（n-1）个公差，用第n项剪去多出的即可。
辅助练习：等差数列……91,95,99共17项，求第一项是多少？分析：已知第17项是99，项数n为17，公差95-91=4答：99-（17-1）×4=35（此公式本讲没有涉及）⒊项数n=（第n项－首项）÷公差+1理解方法：对比植树问题，第n个数与第一个数之间共差了第n项－首项，那么间隔数应为（第n项－首项）÷公差，项数n应该比间隔数多1，所以，项数n=（第n项－首项）÷公差+1此公式为求和公式的基础，往往一道题第一步需要孩子判断一下共有多少项，第二步利用求和公式求和。
第一讲分数四则混合运算一、知识点梳理Ø奥数六大模块：计算，计数，应用题，行程，几何，数论。
Ø本讲属于：计算一、小数的运算法则1、加减法：注意小数点对齐，其余和整数相似2、乘法：看乘数和被乘数里共有几位小数，就从积的右边数出几位，点上小数。
3、除法：需要把除数转化为整数，然后按照整数除法进行二、分数的运算法则1、加减法：分母先通分---找到分母的最小公倍数。
然后分子才可以相加减。
2、乘法：分子相乘的积作为结果的分子，分母相乘的积作为结果的分母，最后记住要进行约分。
3、除法：记住：甲除以乙，等于甲乘乙数的倒数。
重要步骤：约分----------找出分子分母的公约数，利用分数基本性质：分子分母同乘（除）一个不为零的数，值不变三、分数与小数的互化：(1)原则：具体化成哪个取决于用分数简单还是用小数简单。
一般是：乘除法运算时，小数化成分数，这样可以约分。
加减法运算时，分数化成小数，这样避免通分。
(2)熟练掌握一些常见的分数和小数互化，如：1=0.5 2，1=0.25，3=0.754，1=0.1258……..等.(3)分数要约分保留最简形式。
四、百分数1、百分数的符号：%，可以看成1100. 也可以看成乘以0.01如：753 75%=0.75==1004五、繁分数1、定义：分子或分母（都）含有四则运算或分数的数，叫繁分数。
最长的分数线叫主分数线，以上叫分子，以下叫分母。
如：122+3，分子是1，分母是22+3。
二、重点例题讲解（按照相关要求，例题只标出题号，不再书写题目，各位家长见谅）例题5：解析：考察了常用的巧算技巧：乘法分配律和其逆运算。
(1)、原式=21233 15125´+´-=212 545 +-=1 4(2)、原式=111388 1212´+´=1113 (8 1212+´=28´=16例题6：解析：考察凑数法，配对法，计算的时候并不一定要按照给定的顺序计算，先观察题目中数字的特点。
第1讲计算综合（一）繁分数的运算，涉及分数与小数的定义新运算问题，综合性较强的计算问题．1．繁分数的运算必须注意多级分数的处理，如下所示：甚至可以简单地说：“先算短分数线的，后算长分数线的”．找到最长的分数线，将其上视为分子，其下视为分母．2．一般情况下进行分数的乘、除运算使用真分数或假分数，而不使用带分数．所以需将带分数化为假分数．3．某些时候将分数线视为除号，可使繁分数的运算更加直观．4．对于定义新运算，我们只需按题中的定义进行运算即可．5．本讲要求大家对分数运算有很好的掌握，可参阅《思维导引详解》五年级[第1讲循环小数与分数]．1．计算：71147 18262 13581333416⨯+⨯-÷【分析与解】原式=7123723174612241488128131233+⨯=⨯=-2．计算：【分析与解】注意，作为被除数的这个繁分数的分子、分母均含有5199．于是，我们想到改变运算顺序，如果分子与分母在5199后的两个数字的运算结果一致，那么作为被除数的这个繁分数的值为1；如果不一致，也不会增加我们的计算量．所以我们决定改变作为被除数的繁分数的运算顺序．而作为除数的繁分数，我们注意两个加数的分母相似，于是统一通分为1995×．具体过程如下：原式=5919(3 5.22)19930.41.6910()52719950.5199519(6 5.22)950+-⨯÷+⨯-+=5191.3219930.440.40.59()519950.419950.5191.329-⨯⨯⨯÷+⨯⨯-=199320.41()19950.5+÷⨯=0.410.5÷=1143．计算：1111111987-+-【分析与解】原式=11198711986-+=198613973-=198739734．计算：已知=181111+12+1x+4=，则x等于多少【分析与解】方法一：1118x68114x112x7111+11148x62+214x1x+4+====+++++++交叉相乘有88x+66=96x+56，x=1．25．方法二：有11131118821x4+==+++，所以18222133x4+==++；所以13x42+=，那么x=．5．求944,43,443,...,44 (43)个这10个数的和．【分析与解】方法一：944+43+443...44 (43)++个=1044(441)(4441)...(44...41)+-+-++-个=104444444...44 (49)++++-个=1094(999999...999...9)99⨯++++-个=1004[(101)(1001)(10001)...(1000...01)]99⨯-+-+-++--个=914111.1009=49382715919⨯-个.方法二：先计算这10个数的个位数字和为39+4=31⨯；再计算这10个数的十位数字和为4×9=36，加上个位的进位的3，为36339+=；再计算这10个数的百位数字和为4×8=32，加上十位的进位的3，为32335+=；再计算这10个数的千位数字和为4×7=28，加上百位的进位的3，为28331+=；再计算这10个数的万位数字和为4×6=24，加上千位的进位的3，为24327+=；再计算这10个数的十万位数字和为4×5=20，加上万位的进位的2，为20222+=；再计算这10个数的百万位数字和为4×4=16，加上十万位的进位的2，为16218+=；再计算这10个数的千万位数字和为4×3=12，加上百万位的进位的1，为12113+=；再计算这10个数的亿位数字和为4×2=8，加上千万位的进位的1，为819+=；最后计算这10个数的十亿位数字和为4×1=4，加上亿位上没有进位，即为4．所以，这10个数的和为91．6.如图1-1，每一线段的端点上两数之和算作线段的长度，那么图中6条线段的长度之和是多少【分析与解】因为每个端点均有三条线段通过，所以这6条线段的长度之和为：1173(0.60.875)1+0.75+1.8+2.625=6.175=63440⨯+++=7.我们规定，符号“○”表示选择两数中较大数的运算，例如：3．5○=○=．符号“△”表示选择两数中较小数的运算，例如：△=△=．请计算：23155 (0.625)(0.4)33384 1235(0.3)( 2.25) 3104⨯+【分析与解】原式1550.6255155725384218384122562.253⨯=⨯÷=+8．规定（3）=2×3×4，（4）=3×4×5，(5)=4×5×6，(10)=9×10×11，…．如果111(16)(17)(17)-=⨯，那么方框内应填的数是多少【分析与解】111(17)()1(16)(17)(17)(16)=-÷=-=161718111516175⨯⨯-=⨯⨯.9．从和式11111124681012+++++中必须去掉哪两个分数，才能使得余下的分数之和等于1【分析与解】因为1116124+=，所以12,14,16,112的和为l，因此应去掉18与110.10．如图1-2排列在一个圆圈上10个数按顺时针次序可以组成许多个整数部分是一位的循环小数，例如．那么在所有这种数中。
分数基本计算与比例初步内容提要：分数比例分数分数的概念把整体平均分成若干份，表示这样的一份或几份的数叫做分数如25表示把整体平均分成5份，占其中的2份分母表示把一个物体平均分成几份，分子是表示取其中的几份注意：分母不能为0分数的种类真分数：分子比分母小的分数，如2 3假分数：分子比分母大的分数，如3 2带分数：把假分数化成整数和真分数加在一起的分数，如32＝1＋2１＝112分数的性质1．分子和分母同时乘以或除以相同的数(0除外)，分数的大小不变如246369＝＝，8421005025＝＝2．约分与通分约分：分子分母同时除以公因数，如425025＝最简分数通分：把多个分数的分母变成一样，如224833412⨯⨯＝＝比较大小333944312⨯⨯＝＝注意：有时通分也可把分子变成一样3．分数的倒数倒数：乘积为1的两个数互为倒数分数：分子与分母的位置互换注意：0没有倒数分数和小数互化分数化小数：分子除以分母小数化分数：小数点后有1位数，2位数，3位数…，分母分别为10，100，1000…分子就是小数点后的数注意要化成最简分数如2250.4 5÷＝＝0.012＝123 1000250＝分数的运算1．加减法同分母加减法：分母不变，分子相加减，结果化为最简分数异分母加减法：先通分，变为分母相同的分数，分子再相加减如：347888＋＝23342761 917153153153 +=+=2．乘除法乘法：分子乘分子，分母乘分母如3312311 88882243⨯4⨯4=⨯====1⨯133123 8884010 443⨯4⨯=⨯===55⨯5除法：除以一个数等于乘以这个数的倒数如33121 888242 343⨯4÷=⨯===43⨯3注意：分数的乘除法运算过程中可以先约分分数的四则混合运算的规律与整数一样特殊的约分连锁约分 整体约分连锁约分：4433221⨯⨯⨯=122⨯33⨯44⨯1=整体约分：3333123123246369123(123)13526103915135(123)⨯⨯⨯⨯+⨯⨯+⨯⨯⨯⨯⨯++⨯⨯+⨯⨯+⨯⨯⨯⨯⨯++＝＝33(123)⨯++13⨯335(123)⨯⨯++25＝我们来看看分数的乘除法 计算下列各式：28157549⨯＝__________；315711÷＝__________。
学而思小学奥数知识点梳理学而思教材编写组侍春雷前言小学奥数知识点梳理，对于学而思的小学奥数大纲建设尤其必要，不过，对于知识点的概括很可能出现以偏概全挂一漏万的现象，为此，本人参考了单尊主编的《小学数学奥林匹克》、中国少年报社主编的《华杯赛教材》、《华杯赛集训指南》以及学而思的《寒假班系列教材》和华罗庚学校的教材共五套教材，力图打破原有体系，重新整合划分，构建十七块体系（其第十七为解题方法汇集，可补充相应杂题），原则上简明扼要，努力刻画小学奥数知识的主树干。
概述一、计算1．四则混合运算繁分数⑴运算顺序⑵分数、小数混合运算技巧一般而言：①加减运算中，能化成有限小数的统一以小数形式；②乘除运算中，统一以分数形式。
⑶带分数与假分数的互化⑷繁分数的化简2．简便计算⑴凑整思想⑵基准数思想⑶裂项与拆分⑷提取公因数⑸商不变性质⑹改变运算顺序①运算定律的综合运用②连减的性质③ 连除的性质④ 同级运算移项的性质⑤ 增减括号的性质⑥ 变式提取公因数形如：1212......(......)n n a b a b a b a a a b ÷±÷±±÷=±±±÷3． 估算求某式的整数部分：扩缩法4． 比较大小① 通分a. 通分母b. 通分子② 跟“中介”比③ 利用倒数性质 若111a b c >>，则c>b>a.。
形如：312123m m m n n n >>，则312123n n n m m m <<。
5． 定义新运算6． 特殊数列求和运用相关公式：①()21321+=++n n n②()()612121222++=+++n n n n③()21n a n n n n =+=+④()()412121222333+=++=+++n n n n ⑤131171001⨯⨯⨯=⨯=abc abc abcabc⑥()()b a b a b a -+=-22⑦1+2+3+4…（n-1）+n+（n-1）+…4+3+2+1=n 2二、 数论1． 奇偶性问题奇±奇=偶 奇×奇=奇奇±偶=奇奇×偶=偶偶±偶=偶偶×偶=偶2．位值原则形如：abc=100a+10b+c3．数的整除特征：4．整除性质①如果c|a、c|b，那么c|(a±b)。
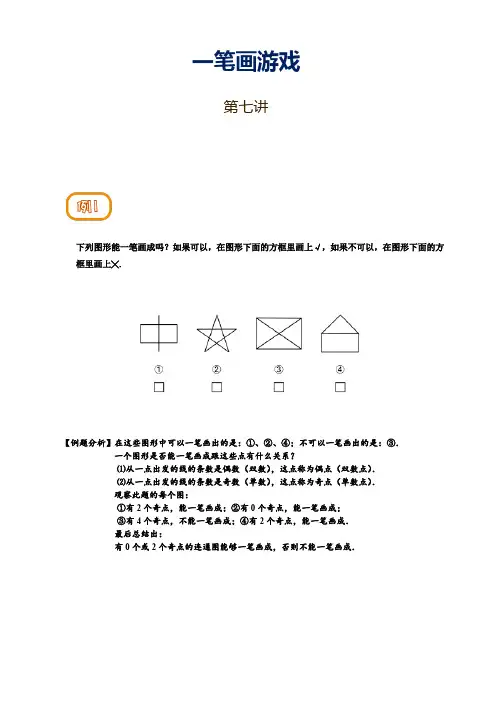
一笔画游戏第七讲下列图形能一笔画成吗？如果可以，在图形下面的方框里画上√，如果不可以，在图形下面的方框里画上╳．【例题分析】在这些图形中可以一笔画出的是：①、②、④；不可以一笔画出的是：③．一个图形是否能一笔画成跟这些点有什么关系？⑴从一点出发的线的条数是偶数（双数），这点称为偶点（双数点）．⑵从一点出发的线的条数是奇数（单数），这点称为奇点（单数点）．观察此题的每个图：①有2个奇点，能一笔画成；②有0个奇点，能一笔画成；③有4个奇点，不能一笔画成；④有2个奇点，能一笔画成．最后总结出：有0个或2个奇点的连通图能够一笔画成，否则不能一笔画成．下列图形能一笔画成吗？为什么？如果可以，在图形下面的方框里画上√，如果不可以，在图形下面的方框里画上╳．【例题分析】①、②、③可以，④不可以．①有2个奇点，②有0个奇点，③有2个奇点，所以①、②、③可以一笔画．④有4个奇点，所以④不能一笔画．下列图形能一笔画成吗？如果可以，在图形下面的方框里画上√，如果不可以，在图形下面的方框里画上╳．【例题分析】①③⑤可以；②④不可以．①有0个奇点；③有2个奇点；⑤有0个奇点；所以①③⑤可以一笔画．②有4个奇点；④有6个奇点；所以②④不能一笔画．【例题分析】⑴ 图①中有4个点是奇点，所以不能一笔画成，要想使这个图形能一笔画成，可以添加一条线段，使这个图形的奇点变成2个．如下图（答案不唯一）：⑵图②因为有4个点是奇点，所以不能一笔画成，要想使这个图形能一笔画成，可以添加一条线段，使这个图形的奇点变成2个．如下图（答案不唯一）：⑶图③中有4个点是奇点，所以不能一笔画成，要想使这个图形一笔画成，可以添加一条线段，使这个图形的奇点变成2个．如下图：下面的图形都不能一笔画成，请你分别在各图中添上一条线段，使它能一笔画成．【例题分析】上图一共有6个奇点，只添一条线段无法变成2个奇点，至少需要添上2条线段．如下图（答案不唯一）：下面的图形都不能一笔画成，请你在各个图中分别去掉一条线，使它能一笔画成，在去掉的线上打╳．下面的图形不能一笔画成，至少添上几条线段才能使它一笔画成？试着添一添．【例题分析】⑴图①中有4个点是奇点，所以不能一笔画成，要想使这个图形能一笔画成，就要使这个图形的奇点变成2个．如下图（答案不唯一）：⑵图②和图①相似，因为有4个点是奇点，所以不能一笔画成，要想使这个图形能一笔画成，就要使这个图形的奇点变成2个．如下图（答案不唯一）：⑶图③中有4个点是奇点，所以不能一笔画成，要想使这个图形一笔画成，就要使这个图形的奇点变成2个．如下图（答案不唯一）：下面的图形不能一笔画成，请你去掉一条线，使它能一笔画成，在去掉的线上打╳．【例题分析】图中有4个点是奇点，所以不能一笔画成，要想使这个图形能一笔画成，就要使这个图形的奇点变成2个．如下图（答案不唯一）：（ ）→（ ）→（ ）→（ ）→（ ）→（ ）→（ ）→（ ）→（ ）→（ ）→（ ）→（ ）→（ ）→（ ）【例题分析】出入口应设在A 、C 两个奇点处．A →B →C →I →A →H →G →I →E →G →F →E →D →C （路线不唯一）． 本题实际上是这个图以哪两点为起点和终点一笔画出的问题，观察上图可以发现仅有两个奇点： A 点与C 点．因此，出入口应设在A 、C 两个奇点处．下图是一个小区街道的平面图．要不重复地走遍每条街道，出入口应设在哪里？请你再设计一条不重复走遍每条街道的行走路线，用字母和箭头表示出来．下图是乡间的小河，上面建有九座桥，你能从其中一个村子出发一次不重复地走遍所有的桥吗？ (每座桥最多只准走一次，陆地上可以重复地走)【例题分析】可以，丁→丙→丁→甲→丁→乙→丙→乙→甲→乙.（路线不唯一）首先将实物图转化成点线图，所有的村庄都转化成点，所有的桥都转化成线（如下图），图中有2个奇点，所以可以一笔画，也就存在一条路线，能够不重复地走遍所有的桥．我国著名数学家陈景润所著《数学趣谈》一书中，有这样一道题：在法国的首都巴黎有一条河，河中有两个小岛，那里的人们建了15座桥把两个小岛和河岸连接起来，如下图所示．那么，从任一岸出发，不重复地走遍所有的桥到达另一岸，能做到吗？【例题分析】能．将实物图转化成点线图，如下图，图中有2个奇点，可以一笔画，也就是说可以从任一岸出发，不重复地走遍所有的桥到达另一岸．如图是一个超市的平面图，超市共有A、B、C、D、E、F六个门，简乐想一次走遍所有通道而又不走重复路线，请你帮他设计一种进出方法．【例题分析】把每一条通道看作是边，通道的交点看作是点(每个门处即为一个点)，可得下图，这样问题就转化为能否从某点出发将图一笔画的问题．观察可知，如上右图中只有两个奇点(点C和点D)，根据一笔画原理可得：将点C和点D分别作为起点和终点，可将右图一笔画出．即简乐从C门(或D门)进超市，一次走遍所有通道后从D门(或C门)出超市，其行进路线为：C→D→E→O→C→B→E→F→A→B→O→D（路线不唯一）．下图是某展览厅的平面图，它由五个展室组成，任意两个展室之间都有门相通，整个展览厅还有一个入口和一个出口，问游人能否一次不重复地穿过所有的门，并且从入口进，从出口出？【例题分析】把每个展室看作一个点，整个展厅的外部也看作一个点，两室之间有门相通，可以看作两点之间有线相连．这样，展厅的平面图就转化成图②，一个实际问题也就转化为这个图能否一笔画成的问题了，即能否从A出发，一笔画完此图，最后再回到A．图②中，所有的点都是偶点，因此，一定可以以A作为起点和终点而一笔画完此图．即游人可以从入口进，一次不重复地穿过所有的门，最后从出口出来．下面仅给出一种参观路线：A→E→B→C→E→F→C→D→F→A．。
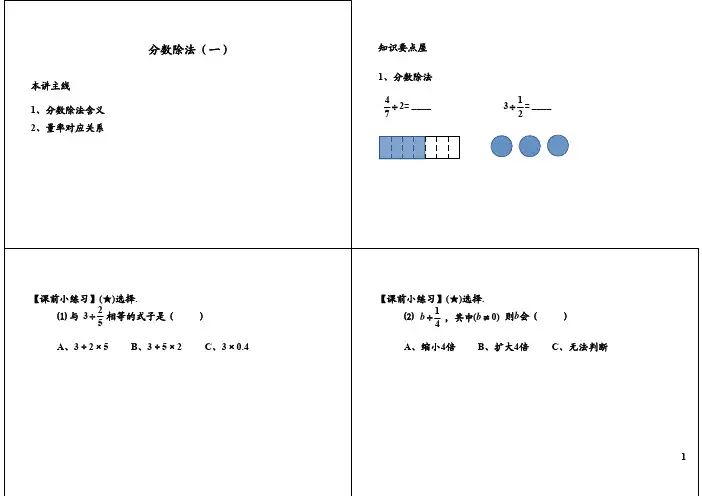
学而思2012年暑假四升五素质123班难题汇总第一讲 分数基本计算分数的性质：分子分母同乘同除一个非零整数，分数的值不变。
倒数的应用：除以一个数，等于乘以这个数的倒数。
裂项的理解：1)n(n 1+=n 1-1n 1+，k)n(n 1+=k 1(n 1-k +n 1)。
11、【例6】计算：603010 (1893126263140)2010...1263842421⨯⨯++⨯⨯+⨯⨯+⨯⨯⨯⨯++⨯⨯+⨯⨯+⨯⨯【难度级别】★★★☆☆【解题思路】本题考察孩子们能否把“1×2×4”和“1×3×6”看成一个整体，而其他各个加数均是这个整体的整数倍。
令1×2×4＝A 、1×3×6＝B ，则： 原式＝B 10...B 3B 2B A10...A 3A 2A ++++++++＝)10...32B(1)10...32A(1++++++++＝B A ＝631421⨯⨯⨯⨯＝94 【答案】9412、【例7】计算：(21+31+41+…+201)+(32+42+52+…+202)+(43+53+…+203)+…+(1918+2018)+2019 【难度级别】★★★★☆【解题思路】分组是本题的关键，将分母相同的分在一组。
先找规律，从分母是20的看，分子是1、2、3、…、19，共19项；进而清楚了，分母是19的有18项（分子依次是1、2、3、…、18），……，分母是3的有2项（分子依次是1、2），分母是2的有1项（分子是1）。
原式＝21+(31+32)+(41+42+43)+…+(201+202+203+…+2019) 对于n ，分子是1+2+3+…+(n-1)的和， (n 1+n 2+n 3+…+n 1-n )=n 1(1+2+3+…+n-1)=n 1×21)-n(n =21)-(n 所以，原式＝21+22+23+…+219＝21×21920⨯＝21×190＝95 【答案】95。
第一专题：计算专题共34讲【强化篇17讲竞赛篇17讲】一、计算竞赛篇共17讲竞赛1-加减法巧算之凑整与组合思想之竞赛篇(第1讲)竞赛2-乘除法巧算之提取公因式与组合思想之竞赛篇(第2讲)竞赛3-四则混合巧算只综合技巧之竞赛篇(第3讲)竞赛4-定义新运算之速算与巧算之竞赛篇(第4讲)竞赛5-数列求和与公式技巧之竞赛篇(第5讲)竞赛6-多位计算与归纳思想之竞赛篇(第6讲)竞赛7-小数计算与换元思想之竞赛篇(第7讲)竞赛8-数表计算与代数公式应用之竞赛篇(第8讲)竞赛9-循环小数互化与错位相减技巧之竞赛篇(第9讲)竞赛10-分数(繁分数)计算综合与比例转化之竞赛篇(第10讲)竞赛11-比较与估算综合技巧之竞赛篇(第11讲)竞赛12-分数计算之拆分、裂项与通项归纳之竞赛篇(第12讲)竞赛13-分数计算之换元与缩放之竞赛篇(第13讲)竞赛14-定义新运算之复杂运算与抽象运算之竞赛篇(第14讲)竞赛15-四大杯赛中的计算综合思想之竞赛篇(第15讲)竞赛16-计算综合之复杂分数裂项计算综合之复杂整数裂项之竞赛篇(第16讲) 竞赛17-计算综合之复杂公式与复杂换元计算之竞赛篇(第17讲)二、计算强化篇共17讲第一讲加减法巧算之凑整与组合思想(第18讲)第二讲乘除法巧算之提取公因式与组合思想(第19讲)第三讲四则混合巧算只综合技巧(第20讲)第四讲定义新运算之速算与巧算(第21讲)第五讲数列求和与公式技巧(第22讲)第六讲多位计算与归纳思想(第23讲)第七讲小数计算与换元思想(第24讲)第八讲数表计算与代数公式应用(第25讲)第九讲循环小数互化与错位相减技巧(第26讲)第十讲分数(繁分数)计算综合与比例转化(第27讲)第十一讲比较与估算综合技巧(第28讲)第十二讲分数计算之拆分、裂项与通项归纳(第29讲)第十三讲分数计算之换元与缩放(第30讲)第十四讲定义新运算之复杂运算与抽象运算(第31讲)第十五讲四大杯赛中的计算综合思想(第32讲)第十六讲计算综合之复杂分数裂项与整数裂项(第33讲)第十七讲计算综合之复杂公式与复杂换元计算(第34讲)第二专题数论专题计算专题共38讲【强化篇19讲竞赛篇19讲】一、数论竞赛篇第一讲奇偶数的性质与应用之竞赛篇(第35讲)第二讲有趣余数之性质与周期之竞赛篇(第36讲)第三讲整数分拆之分类与计数之竞赛篇(第37讲)第四讲整数分拆之最值与应用之竞赛篇(第38讲)第五讲数的整除之性质与求法之竞赛篇(第39讲)第六讲数的整除之代数思想与运用之竞赛篇(第40讲)第七讲数的整除之四大判断法综合运用之竞赛篇(第41讲)第八讲质数、合数与两大约数定理之竞赛篇(第42讲)第九讲因数与倍数之最大公因数与最小公倍数之竞赛篇(第43讲)第十讲因数与倍数之综合应用之竞赛(第44讲)第十一讲完全平方数之竞赛篇(第45讲)第十二讲带余除法之竞赛篇(第46讲)第十三讲同余问题之竞赛篇(第47讲)第十四讲中国剩余定理之竞赛篇(第48讲)第十五讲进制与位值原理之竞赛篇(第49讲)第十六讲四大杯赛的数论综合思想之竞赛篇(第50讲)第十七讲数论综合之整除相关问题之竞赛篇(第51讲)第十八讲数论综合之余数相关问题之竞赛篇(第52讲)第十九讲数论在方程、计数、最值、行程等问题中的应用之竞赛篇(第53讲) 二、数论强化篇第一讲奇偶数的性质与应用(第54讲)第二讲有趣余数之性质与周期(第55讲)第三讲整数分拆之分类与计数(第56讲)第四讲整数分拆之最值与应用(第57讲)第五讲数的整除之性质与求法(第58讲)第六讲数的整除之代数思想与运用(第59讲)第七讲数的整除之四大判断法综合运用(第60讲)第八讲质数、合数与两大约数定理(第61讲)第九讲因数与倍数之最大公因数与最小公倍数(第62讲)第十讲因数与倍数之综合应用(第63讲)第十一讲完全平方数(第64讲)第十二讲带余除法(第65讲)第十三讲同余问题(第66讲)第十四讲中国剩余定理(第67讲)第十五讲进制与位值原理(第68讲)第十六讲四大杯赛中的数论综合思想(第69讲)第十七讲数论综合之整除相关问题(第70讲)第十八讲数论综合之余数相关问题(第71讲)第十九讲数论在方程、计数、最值、行程等问题中的应用之竞赛篇(第72讲) 第三专题行程专题计算专题共30讲【强化篇15讲竞赛篇15讲】一、行程竞赛篇第一讲基础行程之竞赛篇(第73讲)第二讲简单相遇、追及之竞赛篇(第74讲)第三讲复杂相遇、追及之竞赛篇(第75讲)第四讲猎狗追兔之竞赛篇(第76讲)第五讲火车过桥之竞赛篇(第77讲)第六讲多次相遇之竞赛篇(第78讲)第七讲多人行程之竞赛篇(第79讲)第八讲流水行船之竞赛篇(第80讲)第九讲简单环形之竞赛篇(第81讲) 第十讲复杂环形之竞赛篇(第82讲) 第十一讲接送问题之竞赛篇(第83讲) 第十二讲间隔发车之竞赛篇(第84讲) 第十三讲电梯问题之竞赛篇(第85讲) 第十四讲变速变道之竞赛篇(第86讲) 第十五讲综合行程之竞赛篇(第87讲) 二、行程强化篇第一讲基础行程(第88讲)第二讲简单相遇、追及(第89讲)第三讲复杂相遇、追及(第90讲)第四讲猎狗追兔(第91讲)第五讲火车过桥(第92讲)第六讲多次相遇(第93讲)第七讲多次行程(第94讲)第八讲流水行船(第95讲)第九讲简单环形(第96讲)第十讲复杂环形(第97讲)第十一讲接送问题(第98讲)第十二讲间隔发车(第99讲)第十三讲电梯问题(第100讲)第十四讲变速变道(第101讲)第十五讲综合行程(第102讲)第四专题应用题专题共16讲一应用题1和差倍问题(第103讲)盈亏问题(第104讲)二应用题2还原问题(第105讲)鸡兔同笼(第106讲)三应用题3年龄问题(第107讲)周期问题(第108讲)四应用题4平均数问题(第109讲)统筹与规划问题(第110讲)五应用题5分数百分数问题(第111讲)牛吃草(第112讲)六应用题6比和比例(第113讲)工程问题(第114讲)七应用题7经济问题(第115讲)浓度问题(第116讲)八应用题8方程解复杂应用题(第117讲)应用题综合(第118讲)第五专题：几何专题计算专题共4讲【5级2讲6级2讲】一、几何专题能力进阶五级：五大模型及常用思维与方法第一讲五大模型(第119讲)第二讲常用思维与方法(第120讲)二、几何专题能力进阶六级：曲线型与立体几何第一讲曲线型(第121讲)第二讲立体几何(第122讲)。
