非线性模型的线性化
- 格式:pdf
- 大小:446.48 KB
- 文档页数:20




浅谈非线性回归模型的线性化广东省惠州市惠阳区崇雅中学高中部 卢瑞勤(516213)回归分析在各个领域中都有十分重要的作用,比如:在财务中可以用回归分析进行财务预测;在医疗检验中可以用回归分析进行病理预报等等。
高中新课标教材就在《必修3》和《选修2-3》中分别增加了《线性回归》和《回归分析》的内容,介绍了求线性回归方程的方法。
但在实际问题中,变量间的关系并非总是线性关系,本文结合本人的教学实践,对教材中的这两部分内容进行适当延伸,谈谈对一些可线性化的非线性回归模型的线性化问题,供各位同行在教学时参考。
一、什么是可线性化的非线性回归模型线性回归模型的基本特征是预报变量可以表示成解释变量和一个系数相乘的和,即预报变量y 可以表示成解释变量i x (i =1,2,3,……)的如下形式:0112233y a a x a x a x =++++,其中变量ix 是以其原型(而不是以ni x 或其它)的形式出现,变量y 是各变量i x 的线性函数。
而有些回归模型不具备这个特点,但是可以通过适当的代数变换转化成这种形式,我们称这类回归模型为可线性化的回归模型。
在本文中,我们只讨论只有一个解释变量可线性化的非线性回归模型的线性化。
二、非线性回归模型的线性化的基本思路非线性回归模线性化的基本思路是:由已知数据,确定解释变量和预报变量,作出散点图,根据经验,确定回归曲线的类型,然后作适当的代数变换,若变换后散点图体现较好的线性关系,即可将其化成线性形式求解,最后还原到原来的回归曲线。
如果回归曲线可用多种形式表示,可以各自将其线性化后求解,再用相关系数2R 进行拟合效果分析,2R 越大,拟合效果越好,所求的回归方程也就越精确。
三、非线性回归模型的线性化的常用方法可线性化的非线性回归模型有以下几种常见类型:(1)双曲线型,其形式为1a b y x =+,其变换为1y y '=, 1x x'=,变换后的形式为y b ax ''=+ (2)幂函数型,其形式为by ax = ,可以变形为ln ln ln y a b x =+,作变换ln y y '= ,ln x x '= ,变换后的形式为y a bx ''=+(3)指数函数型,其形式为bxy ae = ,以变形为ln ln y a bx =+,作变换ln y y '=,ln a a '= ,变换后的形式为y a bx ''=+(4)对数函数型,其形式为ln y a b x =+,作变换ln x x '=,变换后的形式为y a bx '=+ 下面以高中新课标数学教材《选修2-3》一道习题为例加以说明【例】在某地区的一段时间内观察到的不小于某震级x 的地震个数y 数据如下表,试建立回归方程表述二者之间的关系。


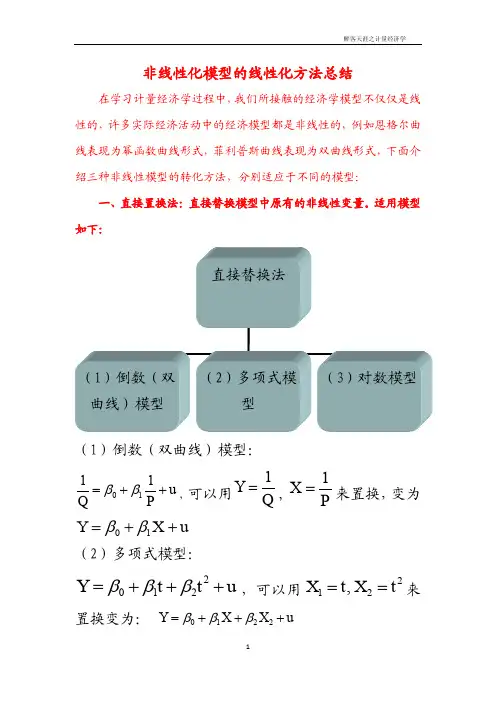
非线性化模型的线性化方法总结在学习计量经济学过程中,我们所接触的经济学模型不仅仅是线性的,许多实际经济活动中的经济模型都是非线性的,例如恩格尔曲线表现为幂函数曲线形式,菲利普斯曲线表现为双曲线形式,下面介绍三种非线性模型的转化方法,分别适应于不同的模型:一、直接置换法:直接替换模型中原有的非线性变量。
适用模型如下:(1)倒数(双曲线)模型:0111u Q P ββ=++,可以用1Y Q =,1X P=来置换,变为01Y X u ββ=++(2)多项式模型:2012Y t t u βββ=+++,可以用212,X t X t ==来置换变为: 0122Y X X u βββ=+++(3)对数模型: 01ln Y X u ββ=++,将1ln X X=带入原式进行置换,得到:011Y X u ββ=++二、函数变换法:通过函数变化,如取对数、移项等方式对原模型进行变形以得到线性化模型:12(,,,)k Y f X X X u =⋅⋅⋅+(1) 幂函数模型:u Q AK L e αβ=,方程两边取对数,得到:ln ln ln ln Q A K L u αβ=+++再对上式进行置换。
(2)指数函数模型:Q uC ab e =,方程两边取对数得到:ln ln ln C a Q b u =++,再对上式进行置换。
三、级数展开法:如CES 函数112()p p u pQ A K L e δδ---=+,方程两边取对数得到:121ln ln ln()p p Q A K L u pδδ--=-++,将式中12ln()p p K L δδ--+在p=0处展开泰勒级数,取关于p 的线性项,即得到一个线性近似式,如取0阶、1阶、2阶项,可得:212121ln ln ln ln [ln()]2K Y A K L p Lδδδδ=++- (备注:无法线性化的模型一般为:12(,,,)k Y f X X X u =⋅⋅⋅+,其中12(,,,)k f X X X ⋅⋅⋅为非线性函数)。

第二章控制系统的数学模型第3讲非线性微分方程的线性化王燕舞为什么要进行线性化?严格的说,几乎所有元件或系统的运动方程都是非线性方程,即输入、输出和扰动等之间的关系都是非线性的。
非线性微分方程的求解和控制系统性能研究非常复杂,而线性化后的模型可借助叠加原理的性质,简化系统分析。
因此,研究非线性微分方程的线性化具有较强的工程实用价值。
什么是非线性数学模型的线性化?在一定的条件下或在一定范围内把非线性的数学模型化为线性模型的处理方法。
符合什么条件的系统可以进行线性化呢?▪条件1: 小偏差理论或小信号理论。
在工程实践中,控制系统都有一个额定的工作状态和工作点,当变量在工作点附近作小范围的变化时,就满足这个条件。
▪条件2: 在工作点附近存在各阶导数或偏导数。
如何进行线性化呢?假设微分方程模型中包含非线性函数f(x)如图所示。
设y=f(x),假设系统在工作点(x 0, y 0), y 0=f(x 0) 附近变化,且在该工作点处各阶导数均存在,在(x 0, y 0)附近将y 展开成泰勒级数:)()()()(000xx x x x f x f x f y -⎥⎦⎤⎢⎣⎡∂∂+==若偏差Δx=x-x 0很小,可忽略级数中高阶无穷小项,上式化为)()()()()()(00000x xK x f x x x x x f x f x f y -+=-⎥⎦⎤⎢⎣⎡∂∂+≈=K 表示y=f(x)曲线在(x 0,y 0)处切线的斜率。
因此非线性函数在工作点处可以用该点的切线方程线性化。
yy=f(x)y 0x 0x ⋯+-⎥⎦⎤⎢⎣⎡∂∂+20022)()(!21x x x x x f xK x f x f y y y ∆=-=-=∆)()(00如何进行线性化呢?小偏差法:在给定工作点的邻域将非线性函数展开为泰勒级数,忽略级数中的高阶项,得到只包含偏差的一次项的线性方程。
液位流体过程。
如图,Q1为流入量,也是输入量;Q 2为流出量;h 为液位高度,为系统输出;C 为液缸的截面积。

