下载文档原格式
7.2 三相异步电动机的空载运行三相异步电动机的定子与转子之间是通过电磁感应联系的。
定子相当于变压器的一次绕组,转子相当于二次绕组，可仿照分析变压器的方式进行分析。
7.2.1 空载运行的电磁关系当三相异步电动机的定子绕组接到对称三相电源时，定子绕组中就通过对称三相交流电流，三相交流电流将在气隙内形成按正弦规律分布，并以同步转速n 1弦转的磁动势F 1。
由旋转磁动势建立气隙主磁场。
这个旋转磁场切割定、转子绕组，分别在定、转子绕组内感应出对称定子电动势，转子绕组电动势和转子绕组电流。
空载时，轴上没有任何机械负载，异步电动机所产生的电磁转矩仅克服了摩擦、风阻的阻转矩，所以是很小的.电机所受阻转矩很小，则其转速接近同步转速，n ≈n 1，转子与旋转磁场的相对转速就接近零，即n 1—n ≈0。
在这样的情况下可以认为旋转磁场不切割转子绕组，则E 2s ≈0（“s"下标表示转子电动势的频率与定子电动势的频率不同），I 2s ≈0.由此可见，异步电动机空载运行时定子上的合成磁动势F 1即是空载磁动势F 10，则建立气隙磁场B m 的励磁磁动势F m 0就是F 10，即F m 0=F 10，产生的磁通为Φm 0.励磁磁动势产生的磁通绝大部分同时与定转子绕组交链，这部分称为主磁通，用φm 表示,主磁通参与能量转换，在电动机中产生有用的电磁转矩。
主磁通的磁路由定转子铁心和气隙组成，它受饱和的影响，为非线性磁路.此外有一小部分磁通仅与定子绕组相交链，称为定子漏磁通φ1σ.漏磁通不参与能量转换并且主要通过空气闭合，受磁路饱和的影响较小，在一定条件下漏磁通的磁路可以看做是线性磁路。
为了方便分析定子、转子的各个物理量,其下标为“1”者是定子方，“2”者为转子方。
异步电动机在正常工作时的一些电磁关系在转子不转时就存在，利用转子不动时分析有助于理解其电磁过程。
一、转子不转时(转子绕组开路）异步电动机内的电磁过程转子绕组开路时,转子电流为零，定子电势和转子电势的大小、频率1E •、2E •和1f ;1）转子绕组开路，定子绕组接三相交流电源， 定子绕组中产生三相对称正弦电流（空载电流），形成幅值固定的气隙旋转磁场，旋转速度为1160f n p =; 2）由于转子不动,旋转磁场在定子绕组、转子绕组中感生频率均为1f 的正弦电动势； 11111222224.444.44{N N E j f k N E j f k N =-Φ=-Φ （7.2)式中k N1、 N 1 ——定子 每相有效串联匝数。
等效电路图的八种画法等效电路又称“等值电路”。
在同样给定条件下，可代替另一电路且对外性能不变的电路。
电机、变压器等电气设备的电磁过程可用其相应的等效电路来分析研究。
等效电路是将一个复杂的电路，通过电阻等效、电容等效，电源等效等方法，化简成具有与原电路功能相同的简单电路。
这个简单的电路，称作原复杂电路的等效电路。
等效电路图的画法步骤1、认真审题，在草稿纸上画出原图，并把开关的状态、滑动变阻器的滑片所处的位置依题意画下；2、根据电流路径的优先走法，把没有电流经过的元件用橡皮擦擦掉，同时将断开的开关及与其串联的元件与擦掉，闭合的开关用导线代替；3、正确分析电路的连接方式，明确电流表测哪部分电路的电流，电压表测谁的电压，再将电路图整理，即画出了等效电路图；4、把已知条件尽可能标注在等效电路图上；5、找出所求的物理量与哪个等效图对应，然后根据串、并联电路的特点，特别注意电源电压不变，定值电阻的阻值不变，正确运用电学公式来分析解答。
等效电路画图的技巧第一种方法叫首尾相接法，如果是全都是首尾相连就一定是串联，如果是首首相连，尾尾相接，就一定是并联。
如果是既有首尾相连，又有首首相连，则一定是混联。
第二种方法叫电流流向法，根据电流的流向，来判断和串并联的特点，来判断串联、并联和混联电路。
第三种方法，叫手捂法，含义是任意去掉一个用电器，其他用电器都不能工作的一定是串联；任意去掉一个用电器，其他用电器都能工作就一定是并联；任意去掉一个用电器，其他用电器部分能工作的一定是混联。
第四种方法，叫节点法1、标出等势点。
依次找出各个等势点，并从高电势点到低电势点顺次标清各等势点字母。
2、捏合等势点画草图。
即把几个电势相同的等势点拉到一起，合为一点，然后假想提起该点“抖动”一下，以理顺从该点向下一个节点电流方向相同的电阻，这样逐点依次画出草图。
画图时要注意标出在每个等势点处电流“兵分几路”及与下一个节点的联接关系。
3、整理电路图。
电阻电路的交流等效电路解析解计算电阻电路是电路中最简单的一类电路，其特点是电流和电压之间的关系符合欧姆定律。
在交流电路中，电压和电流随时间的变化呈现正弦波形，因此需要将电阻电路转换为等效的交流电路进行分析和计算。
本文将介绍电阻电路的交流等效电路解析解的计算方法。
一、电阻电路基本概念回顾在回顾电阻电路的基本概念时，我们知道电阻是指抵抗电流流动的能力，单位为欧姆(Ω)。
电阻的值可以用来描述电阻的大小，越大则电流通过的越困难。
根据欧姆定律，电流(I)等于电压(U)与电阻(R)的比值：I = U/R二、电阻电路的交流等效电路当电阻电路接入交流电源时，电流和电压都会随时间变化，呈现正弦波形。
为了方便分析和计算，我们将电阻电路转换为等效的交流电路。
根据欧姆定律，电流和电压满足以下关系：U = IR在交流电路中，电压和电流的关系可以用复数形式表示：U = U_m * cos(ωt+φ_v)I = I_m * cos(ωt+φ_i)其中，U_m和I_m分别为电压和电流的最大值，ω为角频率，t为时间，φ_v和φ_i为相位差。
将其代入欧姆定律，可得：U_m * cos(ωt+φ_v) = I_m* cos(ωt+φ_i) * R将上式化简得：U_m/R * cos(ωt+φ_v) = I_m * cos(ωt+φ_i)两边取实部，得到等效电路中的电流和电压关系：U_m/R * cos(ωt+φ_v) = I_m * cos(ωt+φ_i)可以看出，在等效电路中，电流和电压的相位差与原电路中的相位差相同，但电压的幅值除以电阻值，得到等效电路中的电流幅值。
三、电阻电路的交流等效电路解析解计算在进行交流等效电路解析解计算时，我们可以利用欧姆定律和复数运算的方法。
1. 计算等效电路中的电流幅值：由等效电路中电流和电压关系的实部得：I_m = U_m/R2. 计算电流和电压的相位差：由等效电路中电流和电压关系得：φ_v = φ_i通过以上两个步骤，我们可以得到电阻电路的交流等效电路的解析解计算结果。
•太阳能电池等效电路分析•引言太阳能电池是利用光伏效应直接将光能转换为电能的器件。
其理想等效电路模型是一个电流源和一个理想二极管的并联电路，其输出特性可以用J—V曲线图表示。
如图1(略）。
在实际器件中，由于表面效应、势垒区载流子的产生及复合、电阻效应等因素的影响,其电流电压特性与理想特性有很大差异，这是因为理想模型不能正确反映实际器件的特点。
实际模型采用串联电阻及并联电阻来等效模拟实际器件中的各种非理想效应的影响。
本文针对太阳电池的等效电路模型，利用Matlab软件建立了仿真模块，模拟了太阳电池各输出参数受其内部电阻影响的程度。
太阳能电池等效电路分析实际太阳电池等效电路如图2所示，由一个电流密度为JL的理想电流源、一个理想二极管D和并联电阻Rsh,串联电阻Rs组合而成。
Rsh为考虑载流子产生与复合以及沿电池边缘的表面漏电流而设计的一个等效并联电阻，Rs为扩散顶区的表面电阻、电池体电阻及上下电极之间的欧姆电阻等复合得到的等效串联电阻。
太阳电池两端的电压为V，流过太阳电池单位面积的电流为J。
由图2可以得出其电流电压关系（公式略）：式中，Js-—二极管反向饱和电流密度。
当太阳电池两端开路时,即负载阻抗为无穷大时，通过太阳电池的净电流J为零,此时的电压为太阳电池的开路电压VOC。
在（1)式中令J=0，则有(公式略)(2）式表明,开路电压不受串联电阻Rs，的影响,但与并联电阻Rsh有关。
可以看出，Rsh减小时，开路电压VOC会随之减小。
太阳电池两端短路即负载阻抗为零时，电压V为零,此时的电流为短路电流密度Jsc.在(1）式中令V=0，并且考虑到一般情况下R 〈<Rsh，(1）式可化为（公式略）由上式可以看出，短路电流基本与Rsh无关,但受Rs,的影响，随着Rs的增大，Js会减小。
太阳电池输出特性仿真以上定性分析了太阳电池等效电路中串联电阻和并联电阻对其伏安特性的影响，并讨论了短路电流和开路电压与电池内部的并联电阻及串联电阻之间的关系。
线性电路的分析方法解析线性电路是由被动元件（如电阻、电容、电感等）和有源元件（如电源、放大器等）组成的一种电路。
线性电路主要通过应用基本电路定律和电路分析方法来分析和解决电路问题。
以下是常见的线性电路分析方法：1.基本电路定律：线性电路分析的基础是基本电路定律，包括欧姆定律（电流与电压成正比关系）、基尔霍夫电压定律（环路电压之和为0）和基尔霍夫电流定律（节点电流之和为0）。
通过这些定律可以建立电路的等式，进一步解决电路问题。
2.等效电路：将复杂的线性电路简化为等效电路是简化分析的常见方法。
等效电路可以用简单的电路元件（如电阻、电流源等）来代替原始电路，但仍然保持电路特性不变。
常见的等效电路包括电阻串联、并联、电流源串联和电压源并联等。
3.节点电压法：节点电压法是一种常用的线性电路分析方法。
它通过将电路中的节点连接到地（或任意选定基准点）上，使用基尔霍夫电流定律分析各节点的电压。
通过列写节点电压方程，可以解得节点的电压值，进而计算电路中的电流和功率等参数。
4.微分方程法：微分方程法是分析线性电路的另一种常见方法。
通过对电路中的元件进行建模，可以得到元件之间的基本关系式，进而得到描述电路行为的微分方程。
通过求解微分方程可以得到电路中的电流和电压等参数。
5.模拟计算：模拟计算是一种常用的线性电路分析方法。
通过使用模拟计算软件，将电路图输入并设置元件参数和初始条件，软件可以自动计算电路中的电流、电压和功率等参数，并绘制相应的波形图。
模拟计算可以方便地分析复杂的线性电路，并可以进行参数的优化和灵敏度分析。
6.相量法：对于交流电路，相量法是一种便捷的分析方法。
相量法将交流电压和电流看作有大小和相位的量，通过将它们用复数表示来进行分析。
通过相量法可以方便地计算交流电路中的电路参数，如电流、电压、功率等。
7.频域分析：频域分析是分析交流电路的另一种常用方法。
频域分析通过将电路中的电压和电流信号进行傅里叶变换，将它们从时域转换为频域。
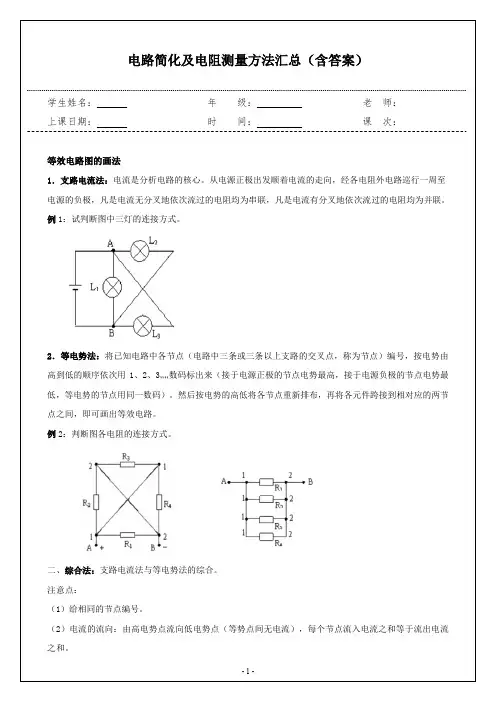
电路简化及电阻测量方法汇总（含答案）学生姓名：年级：老师：上课日期：时间：课次：等效电路图的画法1．支路电流法：电流是分析电路的核心。
从电源正极出发顺着电流的走向，经各电阻外电路巡行一周至电源的负极，凡是电流无分叉地依次流过的电阻均为串联，凡是电流有分叉地依次流过的电阻均为并联。
例1：试判断图中三灯的连接方式。
2．等电势法：将已知电路中各节点（电路中三条或三条以上支路的交叉点，称为节点）编号，按电势由高到低的顺序依次用1、2、3……数码标出来（接于电源正极的节点电势最高，接于电源负极的节点电势最低，等电势的节点用同一数码）。
然后按电势的高低将各节点重新排布，再将各元件跨接到相对应的两节点之间，即可画出等效电路。
例2：判断图各电阻的连接方式。
二、综合法：支路电流法与等电势法的综合。
注意点：（1）给相同的节点编号。
（2）电流的流向：由高电势点流向低电势点（等势点间无电流），每个节点流入电流之和等于流出电流之和。
例3：由5个1Ω电阻连成的如图所示的电路，导线的电阻不计，则A 、B 间的等效电阻为 0.5 Ω。
解:假设A 端为电源正极,则电流中电流方向如图所示根据电流流向可以看出电流分为三路,其中一路只有一个电阻,另外两路分别流过一个电阻后汇合,然后又分为两路,再次各经过一个电阻后与第一路汇合;其等效电路为其等效电阻为.因此，本题正确答案是:0.5.三、含电容器、电流表、电压表的复杂电路：画等效电路时，①电流表视为导线，电容器、电压表视为断路（若考虑内阻，则将其视为一个大电阻），与电容器、电压表串联的用电器视为短路即可。
②画等效电路图的同时，根据图中电流方向将电流表接入电路；根据图中所标节点数字，将电压表和电容器接入电路。
③无电流的支路删去即可直流电路的动态分析 一．程序法。
例1、在右图所示电路中，电源的电功势为E 、内阻为r ，R1，R2，R3，为定值电阻，R 是一滑动变阻器，电路中的电压表和电流表均视为理想的。
电阻网络中的戴维南诺顿等效变换解析实例在电路分析中，戴维南诺顿等效电路是一种常用的方法，用来简化复杂的电阻网络。
通过将电路中的所有电源替换为等效电流源和等效电阻，我们可以更方便地进行电路分析和计算。
本文将通过一个实例，详细介绍戴维南诺顿等效变换的具体步骤和解析方法。
假设我们有一个由多个电阻组成的电路，如下图所示：[图示电路]该电路中包含多个电阻，我们需要对其进行分析，计算出特定端口的电压和电流。
首先，我们要进行戴维南诺顿等效变换，将电源替换为等效电流源和等效电阻。
戴维南诺顿等效变换的步骤如下：步骤一：计算等效电流源的数值在原电路中，我们需要确定特定端口的电流。
为了计算等效电流源，我们需要断开该端口，并用电阻R连接。
然后，通过欧姆定律计算在该电阻上的电压V。
根据欧姆定律，V = I * R，其中I为等效电流源的大小。
步骤二：计算等效电阻的数值在步骤一中，我们已经得到了等效电流源的数值。
现在，我们需要计算等效电阻的大小。
为了计算等效电阻，我们需要在断开的端口处测量开路电压Voc。
然后，用欧姆定律计算在开路电压下的电流Isc。
最后，等效电阻的数值为R = Voc / Isc。
步骤三：确定等效电流源和等效电阻的位置和方向在步骤一和步骤二中，我们已经得到了等效电流源和等效电阻的数值。
现在，我们需要确定它们在电路中的位置和方向。
等效电流源与断开的端口相连，方向与实际电流的方向相反。
等效电阻与实际电阻位置相同。
通过以上步骤，我们成功地将原始电路转化为了戴维南诺顿等效电路。
接下来，我们可以利用等效电路来进行电路分析。
例如，我们希望计算特定端口的电压。
在等效电路中，我们只需要计算等效电源与该端口之间的电压。
通过应用基本的电路分析技巧，结合欧姆定律和基尔霍夫定律，我们可以轻松地计算出所需的电压。
除了计算特定端口的电压之外，戴维南诺顿等效电路还可以用于计算特定端口的电流以及其他电路参数。
通过将复杂的电路简化为等效电流源和等效电阻，我们能更加便捷地进行电路分析，并得到准确的结果。
高中物理解题方法电路等效法 分电流法 等电压法（解析版）一道典型的题目：如图所示的电路，设电压V U AD 12=,电阻Ω=61R ,Ω=32R ,Ω=23R ,电流表A 1/A 2为理想电流表，求电流表A 1/A 2的读数。
【讲解】首先要搞清3个电阻的串并联关系，也就是画出等效电路图，即等效法。
画等效电路图有两个方法，一是分电流法，一是等电压法（等电位法）。
1. 分电流法：从电路一端出发（一般沿电流方向即从电源正极出发），如果遇到分叉就是并联。
本题如图从A 出发，分为两条电路串联，一支过1R 向右，一支过1A 向右；过1A 向右的一支到C 后又分叉，其中一支过3R 向右到D ，另一支？（暂且放下）；过1R 向右的一支到B 后又分叉分叉，其中一支过2A 向右到D, 另一支？（暂且放下） 现在研究R 2上的电流方向，大家知道，电流是从高电位向低电位流的（类比水从高处向地处流），那么B 、C 两点哪点电位高？哪点电位低呢？因为电流表A 1/A 2为理想电流表，即相当于一条导线（电阻为零），所以C 接A 点，B 接D 点，因为V U AD 12=为正，所以A 点电位高于D 点，则C 点电位高于B 点，所以R 2上的电流方向为从C 向B ，即从右向左，那么过1A 向右的一支到C 后又分为两支，其中一支过3R 向右到D, 另一支过2R 向左到B.过1R 向右的一支到B 后不是再分叉，而是与从C 过R 2的一支汇合经A 2到D ，电流方向见下图：2. 等电压法（等电位法）:把电位（即电势）相等的点拉在一起，组成等效电路。
因为A 与C 等电位，B 与D 等电位（都是通过理想电流表相连），所以可以把A 与C ，B 与D 拉到一起，这样可以看出，三个电阻不是串联关系而是并联关系，如图所示：然后再把两个电流表画上去，如下图：从上图可以看出，电流表A1测的是R2和R3的电流之和，即321I I I A +=;电流表A2测的是R1和R2的电流之和，即212I I I A +=。
