2015七下期末试卷3

2015年七年级下册数学期末试卷(含答案)江阴市山观二中2014-2015学年度第二学期初一数学期末试卷2015.6 一、精心选一选：（本大题共8小题，每题3分，共24分） 1．下列运算正确的是（） A、2x+3y=5xy B、5m2•m3=5m5 C、（a―b）2=a2―b2 D、m2•m3=m6 2．已知实数、，若 > ，则下列结论正确的是（）A. B. C. D. 3.等腰三角形的一条边长为6，另一边长为13，则它的周长为（） A． 25 B． 25或32 C． 32 D． 19 4.命题：①对顶角相等；②同一平面内垂直于同一条直线的两直线平行；③相等的角是对顶角；④同位角相等。

其中假命题有（） A．1个 B.2个 C.3个 D.4个 5. 如果关于x、y的方程组x－y=a，3x＋2y=4的解是正数，那么a的取值范围是（） A．－2＜a＜43 B．a＞－43 C．a ＜2 D．a＜－43 6. 下图能说明∠1>∠2的是 ( )7．某校去年有学生1 000名，今年比去年增加4.4%，其中住宿学生增加6%，走读生减少2%。

若设该校去年有住宿学生有x名，走读学生有y名，则根据题意可得方程组 ( ) A. B. C. D. 8.如图，下列图案均是长度相同的火柴按一定的规律拼搭而成：第1个图案需7根火柴，第2个图案需13根火柴，…，依此规律，第11个图案需（）根火柴． A． 156 B． 157 C． 158 D． 159二、细心填一填：（本大题共10小题，每空2分，共22分） 9．拒绝“餐桌浪费”，刻不容缓.据统计全国每年浪费食物总量约50 000 000 000千克，这个数据用科学计数法表示为吨。

10. 若方程组，则3（x+y）�（3x�5y）的值是． 11. 已知10m＝3，10n＝5，则103m－n＝． 12.计算的结果不含和的项，那么m= ；n= . 13．命题“两直线平行，同旁内角相等”是命题（填“真”或“假”）． 14.将一副学生用三角板按如图所示的方式放置．若AE∥BC，则∠AFD的度数是． 15．端午佳节，某商场进行促销活动，将定价为3元的水笔，以下列方式优惠销售：若购买不超过10支，按原价付款；若一次性购买10支以上打八折．如果用30元钱，最多可以购买该水笔的支数是_______． 16.如图，四边形ABCD中，点M，N分别在AB，BC上，将△BMN沿MN翻折，得△FMN，若MF∥AD，FN∥DC, 则∠B = °． 17．若不等式组的解集为3≤x≤4，则不等式ax+b＜0的解集为． 18.若方程组的解是则方程组的解是．三、认真答一答：（本大题共9小题，共54分. ） 19．（4分）计算： 20．（4分）分解因式： 2x4�2 21．（4分）解方程组． 22．解不等式（组）（4分+4分）（1）解不等式：，并把解集表示在数轴上．（2）求不等式组的正整数解．23．（5分）定义：对于实数a，符号[a]表示不大于a的最大整数．例如：[5.7]=5，[5]=5，[�π]=�4．（1）如果[a]=�2，那么a的取值范围是．（2）如果[ ]=3，求满足条件的所有正整数x．24. (6分) 在△ABC中，AE⊥BC于点E，∠BAE:∠CAE＝2:3，BD平分∠ABC，点F在BC上，∠CDF＝30°，∠ABD＝35°．求证：DF⊥BC．25．（6分）甲、乙二人在一环形场地上从A点同时同向匀速跑步，甲的速度是乙的2.5倍，4分钟两人首次相遇，此时乙还需要跑300米才跑完第一圈，求甲、乙二人的速度及环形场地的周长．（列方程（组）求解）26．（8分）某校住校生宿舍有大小两种寝室若干间，据统计该校高一年级男生740人，使用了55间大寝室和50间小寝室，正好住满；女生730人，使用了大寝室50间和小寝室55间，也正好住满．（1）求该校的大小寝室每间各住多少人？（2）预测该校今年招收的高一新生中有不少于630名女生将入住寝室80间，问该校有多少种安排住宿的方案？ 27.（9分）如图，四边形ABCD中，AD∥BC，DE平分∠ADB，∠BDC=∠BCD．（1）求证：∠1+∠2=90°；（2）若H是BC上一动点，F是BA延长线上一点，FH交BD于M，FG 平分∠BFH，交DE于N，交BC于G．当H在BC上运动时（不与B点重合），的值是否变化？如果变化，说明理由；如果不变，试求出其值．初一数学期末考试答案一、选择题：(每题3分，共24分) 题号 1 2 3 4 5 6 7 8 答案 B D C B A C A B 二、填空题：(本大题共10小题，每小题2分，共22分) 9．__ _5×107__ 10．___24___11．___ 5.4 __ 12．_ 4；8____13．_ 假 14．750_ 15． 12 16．__950____17. x〉1.5 18. x=6.3,y=2.2 三、解答题（本大题共9小题，共54分．）19．(本题满分4分) 解：（1）=x2+2x+1-(x2-4)-------------------------2分 =x2+2x+1-x2+4--------------------------3分 =2x+5---------------------------------4分 20．(本题满分4分)解：(2) 原式=2（x4�1） =2（x2+1）（x2�1）--------------------------------------------2分 =2（x2+1）（x+1）（x�1）．------------------------------------4分21．(本题满分4分) 解：，由①得，x=2y+4③，-------------------------------------------1分③代入②得2（2y+4）+y�3=0，解得y=�1，-------------------------------------------2分把y=�1代入③得，x=2×（�1）+4=2，------------------------------------------3分所以，方程组的解是．---------------------------------------------4分22．（1）(本题满分4分) 解：去分母得：2（2x�1）�（9x+2）≤6，----------1分去括号得：4x�2�9x�2≤6，移项得：4x�9x≤6+2+2，合并同类项得：�5x≤10，把x的系数化为1得：x≥�2．------------3分 ----------------------------4分（2）(本题满分4分) 解：解不等式2x+1＞0，得：x＞�，----------------------1 解不等式x＞2x�5得：x＜5，-------------------2分∴不等式组的解集为�＜x＜5，-------------------------3分∵x是正整数，∴x=1、2、3、4、5．--------------------------------------------------4分23．(本题满分5分) （1）�2≤a＜�1--------------------------------------------------------------2分（2）根据题意得：3≤[ ]＜4，-------------------------------------------------3分解得：5≤x＜7，------------------------------------------4分则满足条件的所有正整数为5，6．----------------------------------------5分 24．（本题满分6分）证明:∵BD平分∠ABC，∠ABD=35°∴∠ABC=2∠ABD=70°………………………………………………（2分）∵AE⊥BC ∴∠AEB=90° ∴∠BAE=20°…………………………（3分）又∵∠BAE：∠CAE=2：3 ∴∠CAE=30°………………………（4分）又∵CDF=30° ∴∠CAE=∠CDF …………………………………（5分）∴DF∥AE ∴DF⊥BC……………………………………………（6分） 25．（本题满分6分）解：设乙的速度为x米/秒，则甲的速度为2.5x米/秒，环形场地的周长为y米，-----1分由题意，得，-----------------------------------------------------------------3分解得：，-------------------------------------------------------------------4分∴甲的速度为：2.5×150=375米/分．------------------------------------------------5分答：乙的速度为150米/分，则甲的速度为375米/分，环形场地的周长为900米．-----6分 26．（本题满分8分）解：（1）设该校的大寝室每间住x人，小寝室每间住y人，------------------1分由题意得：，---------------------------------------3分解得：，----------------------------------4分答：该校的大寝室每间住8人，小寝室每间住6人；（2）设大寝室a间，则小寝室（80�a）间，由题意得：，------------------------------------------------------6分解得：80≥a≥75，①a=75时，80�75=5，②a=76时，80�a=4，③a=77时，80�a=3，④a=78时，80�a=2，⑤a=79时，80�a=1，⑥a=80时，80�a=0．故共有6种安排住宿的方案．-----------------------------------8分 27. （本题满分9分）证明：（1）AD∥BC，∠ADC+∠BCD=180，----------------------------------------------1分∵DE平分∠ADB，∴∠ADE=∠EDB，----------------------------------2分∵∠ADC+∠BCD=180°，∠BDC=∠BCD，∴∠EDB+∠BDC=90°，--------------------------------------------3分∠1+∠2=90°．---------------------------------------------------------4分（2） ---------------5分。

七年级（下）期末数学试卷一、仔细选一选（本题有10个小题，每小题3分，共30分）下面每小题给出的四个选项中，只有一个是正确的，请选出正确的选项．注意可以用多种不同的方法来选取正确答案．1．下列各式的计算中，正确的是（）A．﹣2﹣2=﹣4 B．（+1）0=0 C．（﹣）﹣3=27 D．（m2+1）0=12．如图，把一块含有45°角的直角三角板的两个顶点放在直尺的一组对边上，如果∠1=25°，那么∠2的度数是（）A．30°B．25°C．20°D．15°(第2题) (第5题)3．若3x=a，3y=b，则3x﹣2y等于（）A．B．2ab C．a+D．4．若分式方程=2+有增根，则a的值为（）A．4 B．2 C．1 D．05．如图是近年来我国年财政收入同比（与上一年比较）增长率的折线统计图，其中2008年我国财政收入约为61330亿元．下列命题：①2007年我国财政收入约为61330（1﹣19.5%）亿元；②这四年中，2009年我国财政收入最少；③2010年我国财政收入约为61330（1+11.7%）（1+21.3%）亿元．其中正确的有（）A．3个B．2个C．1个D．0个6．计算1÷的结果是（）A．﹣m2﹣2m﹣1 B．﹣m2+2m﹣1 C．m2﹣2m﹣1 D．m2﹣17．已知多项式ax+b与2x2﹣x+2的乘积展开式中不含x的一次项，且常数项为﹣4，则a b的值为（）A．﹣2 B．2 C．﹣1 D．18．为保证某高速公路在2013年底全线顺利通车，某路段规定在若干天内完成修建任务．已知甲队单独完成这项工程比规定时间多用10天，乙队单独完成这项工程比规定时间多用40天，如果甲、乙两队合作，可比规定时间提前14天完成任务．若设规定的时间为x天，由题意列出的方程是（）A．+=B．+=C．﹣=D．+=9．下列不等式变形中，一定正确的是（）A．若ac＞bc，则a＞b B．若a＞b，则ac2＞bc2C．若ac2＞bc2，则a＞b D．若a＞0，b＞0，且，则a＞b10．不等式组的解集是3＜x＜a+2，则a的取值范围是（）A．a＞1 B．a≤3 C．a＜1或a＞3 D．1＜a≤3二、认真填一填（本题有6小题，每小题4分，共24分）要注意认真看清题目的条件和要填写的内容，尽量完整地填写答案．11．分解因式：2x3﹣8xy2=．12．芝麻作为食品和药物，均广泛使用，经测算，一粒芝麻重量约有0.00000201kg，用科学记数法表示10粒芝麻的重量为．13．下列说法中：（1）不相交的两条直线叫做平行线；（2）经过一点，有且只有一条直线与已知直线平行；（3）垂直于同一条直线的两直线平行；（4）直线a∥b，b∥c，则a∥c；（5）两条直线被第三条直线所截，同位角相等．其中正确的是．14．如果关于x的不等式（a﹣1）x＞a+5和2x＞4的解集相同，则a的值为．15．如果x2﹣2（m﹣1）x+m2+3是一个完全平方式，则m=．16．如果记y ==f （x ），并且f （1）表示当x =1时y 的值，即f （1）==；f （）表示当x =时y 的值，即f （）==；…那么f （1）+f （2）+f （）+f （3）+…+f （n +1）+f（）= （结果用含n 的代数式表示）．三、全面答一答（本题有8个小题，共66分．解答应写出文字说明，证明过程或推演步骤，如果觉得有的题目有点困难，那么把自己能写出的解答写出一部分也可以） 17．解下列方程（组）：（1） （2）﹣2=．18．计算：（1）（）﹣1﹣4×（﹣2）﹣2+（﹣π+3.14）0﹣（）﹣2（2）用简便方法计算：1252﹣124×126﹣2101×（﹣0.5）99．19．解不等式组，并从其解集中选取一个能使下面分式有意义的整数，代入求值．20．已知：如图所示，∠ABD和∠BDC的平分线交于E，BE交CD于点F，∠1+∠2=90°．（1）求证：AB∥CD；（2）试探究∠2与∠3的数量关系．21．设b=ma是否存在实数m，使得（2a﹣b）2﹣（a﹣2b）（a+2b）+4a（a+b）能化简为2a2，若能，请求出满足条件的m值；若不能，请说明理由．22．某市为提高学生参与体育活动的积极性，2011年9月围绕“你最喜欢的体育运动项目（只写一项）”这一问题，对初一新生进行随机抽样调查，下图是根据调查结果绘制成的统计图（不完整）．请你根据图中提供的信息解答下列问题：（1）本次抽样调查的样本容量是多少？（2）根据条形统计图中的数据，求扇形统计图中“最喜欢足球运动”的学生数所对应扇形的圆心角度数．（3）请将条形统计图补充完整．（4）若该市2011年约有初一新生21000人，请你估计全市本届学生中“最喜欢足球运动”的学生约有多少人．23．（1）已知a、b、c是△ABC的三边长，试判断代数式（a2+b2﹣c2）2与4a2b2的大小．（2）已知a、b、c是△ABC的三边长，且3a3+6a2b﹣3a2c﹣6abc=0，则△ABC是什么三角形？24．为了抓住世博会商机，某商店决定购进A、B两种世博会纪念品，若购进A种纪念品10件，B 种纪念品5件，需要1000元；若购进A种纪念品5件，B种纪念品3件，需要550元．（1）求购进A、B两种纪念品每件各需多少元？（2）若该商店决定拿出4000元全部用来购进这两种纪念品，考虑市场需求，要求购进A种纪念品的数量不少于B种纪念品数量的6倍，且不超过B钟纪念品数量的8倍，那么该商店共有几种进货方案？（3）若销售每件A种纪念品可获利润20元，每件B种纪念品可获利润30元，在第（2）问的各种进货方案中，哪一种方案获利最大？最大利润是多少？参考答案一、仔细选一选1．解：A、﹣2﹣2=﹣，错误；B、（+1）0=1，错误；C、（﹣）﹣3=﹣27，错误；D、（m2+1）0=1，正确；故选D2．解：∵a∥b，∴∠1=∠3，∵∠2+∠3=45°，∴∠2=45°﹣∠3=45°﹣∠1=20°．故选C3．3x﹣2y=3x÷32y=3x÷32y=3x÷（3y）2=a÷b2=．故选A．4．解：已知方程去分母得：x=2（x﹣4）+a，解得：x=8﹣a，由分式方程有增根，得到x=4，即8﹣a=4，则a=4．故选：A5．解：①2007年的财政收入应该是，不是2007年我国财政收入约为61330（1﹣19.5%）亿元，所以①错．②因为是正增长所以2009年比2007年和2008年都高，所以②错．③2010年我国财政收入约为61330（1+11.7%）（1+21.3%）亿元．所以③正确．故选C．6．解：1÷=1××（m+1）（m﹣1）=﹣（m﹣1）2=﹣m2+2m﹣1．故选B．7．解：∵（ax+b）（2x2﹣x+2）=2ax3+（2b﹣a）x2+（2a﹣b）x+2b，又∵展开式中不含x的一次项，且常数项为﹣4，∴，解得：，∴a b=（﹣1）﹣2=1，选D．8．解：设规定的时间为x天，由题意得，+=．故选D．9．解：A．当c＜0，不等号的方向改变．故此选项错误；B．当c=0时，符号为等号，故此选项错误；C．不等式两边乘（或除以）同一个正数，不等号的方向不变，正确；D．分母越大，分数值越小，故此选项错误．故选C．10．解：根据题意可知a﹣1≤3即a+2≤5，所以a≤3，又因为3＜x＜a+2，即a+2＞3，所以a＞1，所以1＜a≤3，故选：D．二、认真填一填（本题有6小题，每小题4分，共24分）要注意认真看清题目的条件和要填写的内容，尽量完整地填写答案．11．解：∵2x3﹣8xy2=2x（x2﹣4y2）=2x（x+2y）（x﹣2y）．故答案为：2x（x+2y）（x﹣2y）．12．解：0.00000201=2.01×10﹣6，故答案为：2.01×10﹣6．13．解：（1）在同一平面内，不相交的两条直线叫做平行线；故错误；（2）经过直线外一点，有且只有一条直线与已知直线平行；故错误；（3）在同一平面内，垂直于同一条直线的两直线平行；故错误；（4）直线a∥b，b∥c，则a∥c；故正确；（5）两条平行直线被第三条直线所截，同位角相等，故错误．其中正确的是（4）．14．解：由2x＞4得x＞2，∵两个不等式的解集相同，∴由（a﹣1）x＞a+5可得x＞，∴=2，解得a=7．故答案为：7．15．解：∵x2﹣2（m﹣1）x+m2+3是一个完全平方式，∴（m﹣1）2=m2+3，即m2﹣2m+1=m2+3，解得：m=﹣1，故答案为：﹣116．解：∵根据题意，f（2）==，f（）==；f（3）==，f（）==；…f（n+1）=，f（）==；∴f（1）+f（2）+f（）+f（3）+…+f（n+1）+f（）=+++++…++=+1+1+…+1=故答案为：+n．三、全面答一答（本题有8个小题，共66分．解答应写出文字说明，证明过程或推演步骤，如果觉得有的题目有点困难，那么把自己能写出的解答写出一部分也可以）17．解：（1）方程组整理得：，①×6+②×5得：57x=﹣38，解得：x=﹣，把x=﹣代入①得：y=﹣，则方程组的解为；（2）去分母得：x﹣2x+6=3，解得：x=3，经检验x=3是增根，分式方程无解．18．解：（1）原式=2﹣4×+1﹣9=﹣7；（2）原式=1252﹣（125﹣1）×（125+1）﹣2×（﹣2×0.5）99=1252﹣1252+1+2=3．19．解：，由①得，x＜2，由②得，x＞﹣3，所以，不等式组的解集是﹣3＜x＜2，÷﹣=×﹣=﹣=，分式有意义，则x2﹣1≠0，3x≠0，解得x≠±1，x≠0，所以，使得分式有意义的整数只有﹣2，代入得：原式===．20．解：（2）∵DE平分∠BDC，∴∠2=∠FDE；∵∠1+∠2=90°，∴∠BED=∠DEF=90°；∴∠3+∠FDE=90°；∴∠2+∠3=90°．21．解：不能化简为2a2，理由：∵设b=ma，∴（2a﹣b）2﹣（a﹣2b）（a+2b）+4a（a+b）=4a2﹣4ab+b2﹣a2+4b2+4ab+4a2=7a2+5b2=7a2+5（ma）2=7a2+5m2a2=（7+5m2）a2=2a2，故7+5m2=2，解得：5m2=﹣5，不合题意，错误．22．解：（1）100÷20%=500，∴本次抽样调查的样本容量是500；（2）∵360°×=43.2°，∴扇形统计图中“最喜欢足球运动”的学生数所对应的扇形圆心角度数为43.2°；（3）如图：（4）21000×=2520（人）全市本届学生中“最喜欢足球运动”的学生约有2520人；23．解：（1）（a2+b2﹣c2）2﹣4a2b2第11页（共11页）=（a 2+b 2﹣c 2+2ab ）（a 2+b 2﹣c 2﹣2ab ）=[（a +b ）2﹣c 2][（a ﹣b ）2﹣c 2]=（a +b +c ）（a +b ﹣c ）（a ﹣b ﹣c ）（a ﹣b +c ），∵a ，b ，c 是三角形ABC 三边，∴a +b +c ＞0，a +b ﹣c ＞0，a ﹣b ﹣c ＜0，a ﹣b +c ＞0，∴（a +b +c ）（a +b ﹣c ）（a ﹣b ﹣c ）（a ﹣b +C ）＜0，即值为负数，（a 2+b 2﹣c 2）2＜4a 2b 2（2）3a 3+6a 2b ﹣3a 2c ﹣6abc =0，可得：a （a ﹣c ）（a +2b ）=0，所以a =c ，所以△ABC 是等腰三角形．24．解：（1）设我校购进一件A 种纪念品需要a 元，购进一件B 种纪念品需要b 元，由题意，得，∴解方程组得：答：购进一件A 种纪念品需要50元，购进一件B 种纪念品需要100元．（2）设我校购进A 种纪念品x 个，购进B 种纪念品y 个，由题意，得则，解得，解得：20≤y ≤25 ∵y 为正整数∴y =20，21，22，23，24，25答：共有6种进货方案；（3）设总利润为W 元，由题意，得W =20x +30y =20（200﹣2 y ）+30y =﹣10y +4000（20≤y ≤25）∵﹣10＜0，∴W 随y 的增大而减小，∴当y =20时，W 有最大值W 最大=﹣10×20+4000=3800（元）答：当购进A 种纪念品160件，B 种纪念品20件时，可获最大利润，最大利润是3800元．。

2014-2015学年河北省石家庄市七年级（下）期末数学试卷一、选择（每小题2分）1．（2分）若a＞b，则下列不等式变形正确的是（）A．a+5＜b+5 B．C．﹣4a＞﹣4b D．3a﹣2＜3b﹣22．（2分）不等式组的解集是（）A．x≤2 B．x＜﹣1 C．x≥2 D．﹣1＜x≤23．（2分）如图，平面上直线a、b分别过线段AB两端点（数据如图），则a、b 相交所成的锐角是（）A．20°B．30°C．80°D．100°4．（2分）若（x﹣5）（x+20）=x2+mx+n，则m、n的值分别为（）A．m=﹣15，n=﹣100 B．m=25，n=﹣100 C．m=25，n=100 D．m=15，n=﹣1005．（2分）已知是方程2x﹣ay=3的一个解，那么a的值是（）A．1 B．3 C．﹣3 D．﹣16．（2分）如果在△ABC中，∠A=60°+∠B+∠C，则∠A等于（）A．30°B．60°C．120° D．140°7．（2分）下列运算中正确的是（）A．a5+a5=2a5B．a3a2=a6C．a6÷a3=a2D．（a3）4=a78．（2分）如图，将△ABC沿射线BC方向移动，使点B移动到点C，得到△DCE，连接AE，若△ABC的面积为2，则△ACE的面积为（）A．2 B．4 C．8 D．169．（2分）如图，AF是∠BAC的平分线，EF∥AC交AB于点E，若∠1=35°，则∠BAF的度数为（）A．60°B．70°C．35°D．17.5°10．（2分）若a m=15，a n=5，则a m﹣n等于（）A．15 B．10 C．75 D．311．（2分）有若干张面积分别为a2、b2、ab的正方形和长方形纸片，小明从中抽取了1张面积为b2的正方形纸片，6张面积为ab的长方形纸片．若他想拼成一个大正方形，则还需要抽取面积为a2的正方形纸片（）A．4张 B．8张 C．9张 D．10张12．（2分）已知正整数中a、b、c，c=7且a＜b＜c，则以a、b、c为三边长的三角形共有（）A．4个 B．5个 C．6个 D．7个二、填空题（共6小题，每小题3分，满分18分）13．（3分）计算：20152﹣20142=．14．（3分）如图，有一个与地面成30°角的斜坡，现要在斜坡上竖一电线杆，当电线杆与地面垂直时，它与斜坡所成的角α=°．15．（3分）若x2+mx+16是完全平方式，则m=．16．（3分）将一副直角三角尺如图放置，已知AB∥DE，则∠AFC=度．17．（3分）如图，一张长为20cm，宽为5cm的长方形纸片ABCD，分别在边AB、CD上取点M，N，沿MN折叠纸片，BM与DN交于点K，得到△MNK，则△MNK 的面积的最小值是cm2．18．（3分）如图，点O、A在数轴上表示的数分别是0，0.1，将线段OA分成100等份，其分点由左向右依次为M1，M2…M99，再将线段OM1分成100等份，其分点由左向右依次为N1，N2，…N99，则点N15所表示的数用科学记数法表示为．三、细心解答（每小题6分）19．（6分）解方程组：．20．（6分）已知x2﹣3x=1，求代数式（x﹣1）（3x+1）﹣（x+2）2﹣4的值．21．（6分）解不等式组，并写出不等式组的整数解．22．（6分）如图，AB∥CD，AE交CD于点C，DE⊥AE，垂足为E，∠A=37°，求∠D的度数．四、实验与应用23．（8分）如图，已知△ABC中，AB=2，BC=4（1）画出△ABC的高AD和CE；（2）若AD=，求CE的长．24．（8分）定义新运算：对于任意实数，a、b，都有a⊕b=a（a﹣b）+1，等式右边是通常的加法、减法及乘法运算，比如：2⊕5=2（2﹣5）+1=2×﹣（﹣3）+1=﹣6+1=﹣5（1）求3⊕（﹣4）的值；（2）若4⊕x的值大于9，求x的取值范围．25．（9分）已知△ABC中，AE平分∠BAC（1）如图1，若AD⊥BC于点D，∠B=72°，∠C=36°，求∠DAE的度数；（2）如图2，P为AE上一个动点（P不与A、E重合，PF⊥BC于点F，若∠B＞∠C，则∠EPF=是否成立，并说明理由．26．（9分）在实施防污减排战略之际，我市计划对A、B两类化工厂的排污设备进行改造，经预算，改造一个A类工厂和两个B类工厂共需320万元，改造两个A类工厂和一个B类化工厂黄需220万元．（1）改造一个A类化工厂和一个B类化工厂各需多少万元；（2）我市计划改造A、B两类化工厂共10个，改造资金一部分由工厂承担，一部分由市政府补贴，每个A类化工厂可投入自身改造资金20万元，每个B类化工厂可投入自身改造资金30万元，若市财政补贴的资金不超过600万元，那么至少改造几个A类化工厂？2014-2015学年河北省石家庄市七年级（下）期末数学试卷参考答案与试题解析一、选择（每小题2分）1．（2分）若a＞b，则下列不等式变形正确的是（）A．a+5＜b+5 B．C．﹣4a＞﹣4b D．3a﹣2＜3b﹣2【解答】解：由a＞b，变形得：＞，故选：B．2．（2分）不等式组的解集是（）A．x≤2 B．x＜﹣1 C．x≥2 D．﹣1＜x≤2【解答】解：，解①得：x≤2，解②得，x＜﹣1，∴不等式的解集为：x＜﹣1．故选：B．3．（2分）如图，平面上直线a、b分别过线段AB两端点（数据如图），则a、b 相交所成的锐角是（）A．20°B．30°C．80°D．100°【解答】解：a，b相交所成的锐角=100°﹣80°=20°．故选：A．4．（2分）若（x﹣5）（x+20）=x2+mx+n，则m、n的值分别为（）A．m=﹣15，n=﹣100 B．m=25，n=﹣100 C．m=25，n=100 D．m=15，n=﹣100【解答】解：∵（x﹣5）（x+20）=x2+15x﹣100=x2+mx+n，∴m=15，n=﹣100，故选：D．5．（2分）已知是方程2x﹣ay=3的一个解，那么a的值是（）A．1 B．3 C．﹣3 D．﹣1【解答】解：∵是方程2x﹣ay=3的一个解，∴满足方程2x﹣ay=3，∴2×1﹣（﹣1）a=3，即2+a=3，解得a=1．故选：A．6．（2分）如果在△ABC中，∠A=60°+∠B+∠C，则∠A等于（）A．30°B．60°C．120° D．140°【解答】解：∵△ABC中，∠A+∠B+∠C=180°，∴∠B+∠C=180°﹣∠A，∵∠A=60°+∠B+∠C，∴∠A=240°﹣∠A，∴∠A=120°，故选：C．7．（2分）下列运算中正确的是（）A．a5+a5=2a5B．a3a2=a6C．a6÷a3=a2D．（a3）4=a7【解答】解：A、a5+a5=2a5，故A选项正确；B、a3a2=a5，故B选项错误；C、a6÷a3=a3，故C选项正确；D、（a3）4=a12，故D选项错误．故选：A．8．（2分）如图，将△ABC沿射线BC方向移动，使点B移动到点C，得到△DCE，连接AE，若△ABC的面积为2，则△ACE的面积为（）A．2 B．4 C．8 D．16【解答】解：∵将△ABC沿射线BC方向移动，使点B移动到点C，得到△DCE，∴BC=CE，∴△ACE的面积等于△ABC的面积，又∵△ABC的面积为2，∴△ACE的面积为2．故选：A．9．（2分）如图，AF是∠BAC的平分线，EF∥AC交AB于点E，若∠1=35°，则∠BAF的度数为（）A．60°B．70°C．35°D．17.5°【解答】解：∵EF∥AC，∴∠FAC=∠1=35°，∵AF是∠BAC的平分线，∴∠BAF=∠FAC=35°，故选：C．10．（2分）若a m=15，a n=5，则a m﹣n等于（）A．15 B．10 C．75 D．3【解答】解：a m﹣n=a m÷a n=15÷5=3，故选D11．（2分）有若干张面积分别为a2、b2、ab的正方形和长方形纸片，小明从中抽取了1张面积为b2的正方形纸片，6张面积为ab的长方形纸片．若他想拼成一个大正方形，则还需要抽取面积为a2的正方形纸片（）A．4张 B．8张 C．9张 D．10张【解答】解：∵要拼成正方形，∴b2+6ab+ka2是完全平方式，∵（b+3a）（b+3a）=b2+6ab+9a2，∴还需面积为a2的正方形纸片9张．故选：C．12．（2分）已知正整数中a、b、c，c=7且a＜b＜c，则以a、b、c为三边长的三角形共有（）A．4个 B．5个 C．6个 D．7个【解答】解：∵三角形的三边a、b、c的长都是整数，且a＜b＜c，c最大为7，∴a=2，b=6，c=7；a=3，b=6，c=7；a=4，b=6，c=7；a=5，b=6，c=7；a=3，b=5，c=7；a=4，b=5，c=7；故存在以a、b、c为三边长的三角形的个数为6个．故选：C．二、填空题（共6小题，每小题3分，满分18分）13．（3分）计算：20152﹣20142=4029．【解答】解：20152﹣20142=（2015+2014）（2015﹣2014）=4029．故答案为：4029．14．（3分）如图，有一个与地面成30°角的斜坡，现要在斜坡上竖一电线杆，当电线杆与地面垂直时，它与斜坡所成的角α=60°．【解答】解：如图，延长电线杆与地面相交，∵电线杆与地面垂直，∴∠1=90°﹣30°=60°，由对顶角相等，∠α=∠1=60°．故答案为：60．15．（3分）若x2+mx+16是完全平方式，则m=±8．【解答】解：∵x2+mx+16是完全平方式，∴m=±8．故答案为：±8．16．（3分）将一副直角三角尺如图放置，已知AB∥DE，则∠AFC=75度．【解答】解：∵AB∥DE，∴∠B=∠BCD=45°，∵∠D=30°，∴∠AFC=∠D+∠BCD=75°，故答案为：75°17．（3分）如图，一张长为20cm，宽为5cm的长方形纸片ABCD，分别在边AB、CD上取点M，N，沿MN折叠纸片，BM与DN交于点K，得到△MNK，则△MNK 的面积的最小值是12.5cm2．【解答】解：由折叠的性质得：∠1=∠KMN，∵四边形ABCD是矩形，∴AD=BC=5cm，AB∥DC，∴∠KNM=∠1，∴∠KMN=∠KNM，∴KM=KN，∴当KM=KN=BC=5cm时，△MNK的面积最小，△MNK的最小值=×5×5=12.5（cm2）；故答案为：12.5．18．（3分）如图，点O、A在数轴上表示的数分别是0，0.1，将线段OA分成100等份，其分点由左向右依次为M1，M2…M99，再将线段OM1分成100等份，其分点由左向右依次为N1，N2，…N99，则点N15所表示的数用科学记数法表示为 1.5×10﹣4．【解答】解：∵OM1=OA×=0.1×=0.001，ON1=OM1×=0.00001，∴点N15所表示的数为：0.00001×15=0.00015，∴0.00015=1.5×10﹣4，故答案为：1.5×10﹣4．三、细心解答（每小题6分）19．（6分）解方程组：．【解答】解：，①+②得：7x=14，即x=2，把x=2代入①得：y=2，则方程组的解为．20．（6分）已知x2﹣3x=1，求代数式（x﹣1）（3x+1）﹣（x+2）2﹣4的值．【解答】解：原式=3x2﹣2x﹣1﹣（x2+4x+4）﹣4=3x2﹣2x﹣1﹣x2﹣4x﹣4﹣4=2x2﹣6x﹣9．∵x2﹣3x=1．∴原式=2（x2﹣3x）﹣9=2﹣9=﹣7．21．（6分）解不等式组，并写出不等式组的整数解．【解答】解：由①得：x≤3，由②得：x＞﹣1，）∴不等式组的解集为：﹣1＜x≤3；∴不等式组的整数解：0，1，2，3．22．（6分）如图，AB∥CD，AE交CD于点C，DE⊥AE，垂足为E，∠A=37°，求∠D的度数．【解答】解：∵AB∥CD，∠A=37°，∴∠ECD=∠A=37°．∵DE⊥AE，∴∠D=90°﹣∠ECD=90°﹣37°=53°．四、实验与应用23．（8分）如图，已知△ABC中，AB=2，BC=4（1）画出△ABC的高AD和CE；（2）若AD=，求CE的长．【解答】解：（1）如图：=×AD×BC=AB×CE，（2）∵S△ABC∴××4=×2×CE，∴CE=3．24．（8分）定义新运算：对于任意实数，a、b，都有a⊕b=a（a﹣b）+1，等式右边是通常的加法、减法及乘法运算，比如：2⊕5=2（2﹣5）+1=2×﹣（﹣3）+1=﹣6+1=﹣5（1）求3⊕（﹣4）的值；（2）若4⊕x的值大于9，求x的取值范围．【解答】解：（1）3⊕（﹣4）=3（3+4）+1=22；（2）4⊕x=4（4﹣x）+1=17﹣4x，则17﹣4x＞9，解得：x＜2．25．（9分）已知△ABC中，AE平分∠BAC（1）如图1，若AD⊥BC于点D，∠B=72°，∠C=36°，求∠DAE的度数；（2）如图2，P为AE上一个动点（P不与A、E重合，PF⊥BC于点F，若∠B＞∠C，则∠EPF=是否成立，并说明理由．【解答】证明：（1）如图1，∵∠B=72°，∠C=36°，∴∠A=180°﹣∠B﹣∠C=72°；又∵AE平分∠BAC，∴∠1==72°，∴∠3=∠1+∠C=72°，又∵AD⊥BC于D，∴∠2=90°，∴∠DAE=180°﹣∠2﹣∠3=18°．（2）成立．如图2，∵AE平分∠BAC，∴∠1===90°﹣，∴∠3=∠1+∠C=90°﹣+，又∵PF⊥BC于F，∴∠2=90°，∴∠EPF=180°﹣∠2﹣∠3=．26．（9分）在实施防污减排战略之际，我市计划对A、B两类化工厂的排污设备进行改造，经预算，改造一个A类工厂和两个B类工厂共需320万元，改造两个A类工厂和一个B类化工厂黄需220万元．（1）改造一个A类化工厂和一个B类化工厂各需多少万元；（2）我市计划改造A、B两类化工厂共10个，改造资金一部分由工厂承担，一部分由市政府补贴，每个A类化工厂可投入自身改造资金20万元，每个B类化工厂可投入自身改造资金30万元，若市财政补贴的资金不超过600万元，那么至少改造几个A类化工厂？【解答】解：（1）设改造一个A类化工厂需资金x万元，改造一个B类化工厂需资金y万元，根据题意得：，解得：．答：改造一个A 类化工厂需资金40万元，改造一个B 类化工厂需资金140万元．（2）设可改造a 个A 类化工厂，则B 类化工厂有（10﹣a ）个可改造． 根据题意得：a （40﹣20）+（10﹣a ）（140﹣30）≤600，解得：a ≥5．答：至少改造6个A 类化工厂．赠送：初中数学几何模型举例 【模型四】几何最值模型：图形特征： PA Bl运用举例：1. △ABC 中，AB =6，AC =8，BC =10，P 为边BC 上一动点，PE ⊥AB 于E ，PF ⊥AC 于F ，M 为AP 的中点，则MF 的最小值为 M FEB2.如图，在边长为6的菱形ABCD 中，∠BAD ＝60°，E 为AB 的中点，F 为AC 上一动点，则EF +BF 的最小值为_________。

2015学年第二学期七年级数学期末考试卷(完卷时间：90分钟 满分：100分)2’×15=30’）．16的平方根等于 ．=___________. ．用幂的形式表示：343＝ ．“>”，“=”，“<” ）．近似数51.47510⨯有____________个有效数字．已知点P （－3，4）与点Q 关于原点对称，那么点Q 的坐标是 ． 经过点M （－1，2）且平行于y 轴的直线为直线_________________． 如果点P （m ，1﹣3m ）在第四象限，那么m 的取值范围是 ． 如果等腰三角形的顶角为60°，底边长为5，那么它的腰长= ．在△ABC 中，如果::1:3:5A B C ∠∠∠=，那么△ABC 是 三角形（按角分类）． 如图，已知直线a // b ，∠1 = 48°，那么∠2 = 度．在直角坐标平面内有一个三角形，它的三个顶点坐标分别是A （-1，5）、B （3，5）C （2，-1），那么这个三角形的面积等于 ．如图，将△ABC 的一角折叠，使点C 落在△ABC 内的D 点处，折痕与AC 、BC 两边分别交于E 、F 两点，如果∠A = 55°，∠B = 75°，DE // BC ，那么∠BFD = 度． 在△ABC 中，AB = AC ，BD 、CE 分别是∠ABC 和∠ACB 的角平分线，图中有 对全等三角形．如图，在△ABC 中，∠A =120°，∠B = 40°，过A 画一条直线l 把△ABC 分割成两个等腰l 与BC相交于D ，那么∠ADC =____________度．二、选择题（2’×5=10’）16. 下列计算正确的是………………………………………………（ ） （A 9=±（B ）6)6(2=-（C ）5)5(2-=- （D ）4131619= 17. 在平面直角坐标系中，如果点()b a P ，到x 轴的距离为2，那么………………………（ ） （A ）2=a（B ）2±=a（C ）2=b（D ）2±=b18．如图，下列条件不能判定AB ∥CD 的是……………………………（ ）．（A ）∠1=∠2； （B ）∠3=∠4； （C ）∠B +∠BCD =180°； （D ）∠B =∠5．19．下列说法正确的是……………（ ）． （第18题图）（A ）两个等边三角形一定全等； （B ）腰对应相等的两个等腰三角形全等； （C ）形状相同的两个三角形全等； （D ）全等三角形的面积一定相等．20. 有四根细木棒，长度分别为3cm ，5cm ，7cm ，9cm ，现任取其中的三根木棒，组 成一个三角形，问：有几种可能？…………………………………………………（ ） （A ）1种； （B ）2种； （C ）3种； （D ）4种． 三、简答题（21、22、23每题6分，24、25每题8分，共34分） 21. 计算：3)323(-)7()3(22÷-+- 22. 计算：119732427()()98-+-÷23. 如图，已知：AB //CD ，AD //BC ，()504+=∠x A ，⎪⎭⎫⎝⎛+=∠8025x C ．求∠A 的度数．l a b12（第11题图）（第13题图）54 3 2 1 ED CBA （第23题图）DCBA ABE D（第14题图）……………………………………密……………………………封………………………线………………………………………………24．如图，已知△ABC 中，∠C = 90°，CA = CB ，AD 平分∠CAB 交BC 于D ，DE ⊥AB . （1）说明△ADC ≌△ADE 的理由；（2）若AB = 8，求△DEB 的周长.25. 在直角坐标平面内，点A 的坐标为（2，0） （1）图中点B 点的坐标是_____________；（2）点B 关于原点对称的点C 的坐标是_________；点B 关于y 轴对称的点D 的坐标是 ；（3）请画出△ABC ；则△ABC 的面积是_________； （4）在x 轴上找一点E ，使得△ADE 的面积等于△ABC 的面积，那么点E 的所有可能的位置是 __________________________．（用坐标表示）四、解答题（8’ +8’+10’＝26’）26． 如图，在四边形ABCD 中，AD ∥ BC ，E 是AB 的中点，连接DE 并延长交CB 的延长线于点F ，点G 在边BC 上，且∠ 1=∠ 2． （1）求证：△ ADE ≌ △ BFE ；（2）联结EG ，试说明EG 与DF 垂直的理由． 解：EG FD B A 2127．已知：如图，在直角坐标平面内，O 为原点，点A （3，4）．将线段OA 绕原点O 旋转90°后，线段OA 旋转至线段OB ．求点B 的坐标．28．已知：如图，等边△ABC ，点D 是边AC 上任意一点，射线CE //AB ，在射线CE 上截取CF ，使CF ＝AD ．分别联结BD 、DF 、FB ． （1）判断△BDF 的形状，并说明理由； （2）如果点D 是AC 的中点，①画出△BDF ；（不写画法）②判断线段BC 与DF 所在直线的位置关系，并说明理由．（第28题图）FEDCBA（备用图）ECBA(第27题图)。

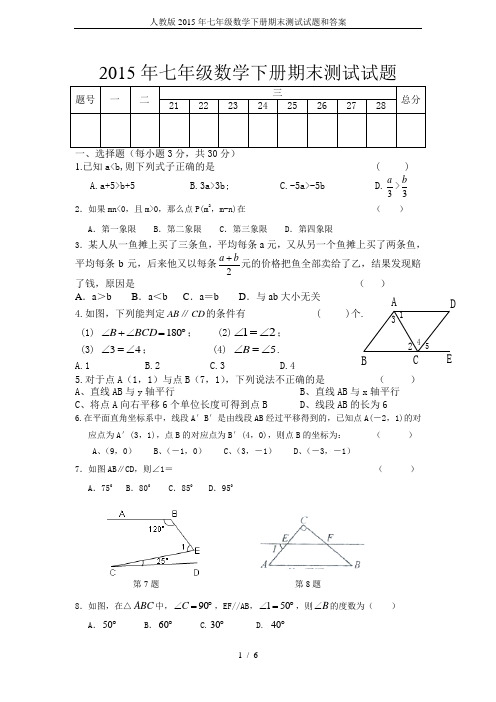
54D3E21C BA第7题第8题2015年七年级数学下册期末测试试题1.已知a<b,则下列式子正确的是 ( )A.a+5>b+5B.3a>3b;C.-5a>-5bD.3a >3b2．如果mn<0，且m>0，那么点P(m 2，m-n)在 （ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限3．某人从一鱼摊上买了三条鱼，平均每条a 元，又从另一个鱼摊上买了两条鱼，平均每条b 元，后来他又以每条2ba +元的价格把鱼全部卖给了乙，结果发现赔了钱，原因是 （ ） A ．a ＞b B ．a ＜b C ．a ＝b D ．与ab 大小无关4.如图，下列能判定AB ∥CD 的条件有 ( )个.(1) ︒=∠+∠180BCD B ； (2)21∠=∠； (3) 43∠=∠； (4) 5∠=∠B .A.1B.2C.3D.45.对于点A （1，1）与点B （7，1），下列说法不正确的是 （ ） A 、直线AB 与y 轴平行 B 、直线AB 与x 轴平行 C 、将点A 向右平移6个单位长度可得到点B D 、线段AB 的长为66.在平面直角坐标系中，线段A ′B ′是由线段AB 经过平移得到的，已知点A(－2，1)的对应点为A ′(3，1)，点B 的对应点为B ′(4，0)，则点B 的坐标为： （ ） A 、（9，0） B 、（－1，0） C 、（3，－1） D 、（－3，－1）7．如图AB∥CD，则∠1＝ （ ） A ．75B ．80C ．85D ．958．如图，在△ABC 中，90C ∠=︒，EF//AB ，150∠=︒，则B ∠的度数为（ ） A ．50︒ B ．60︒ C.30︒ D. 40︒9.如图，AB ∥CD ，∠BAC 与∠DCA 的平分线相交于点G ，GE ⊥AC 于点E ， F 为AC 上的一点，且FA ＝FG ＝FC ，GH ⊥CD 于H.下列说法：① AG ⊥CG ； ②∠BAG ＝∠CGE ； ③S △AFG ＝S △CFG ；④若∠EGH ︰∠ECH ＝2︰7，则∠EGF ＝50°. 其中正确( )(A) ①②③④ (B) ②③④ (C) ①③④ (D) ①②④10.若不等式组⎩⎨⎧>≤11x mx 无解，则m 的取值范围是( )A. m ＜11B. m ＞11C. m ≤11D. m ≥11二、填空题（每题3分，共30分）11、()25-的平方根是 ，-0.027的立方根是 。

2015-2016学年度七年级下册语文期末考试试卷及答案2015年XXX七年级语文下册期末考试共分四大题，共计24小题，总分为120分，考试时间为120分钟。

一、词语积累与运用（27分）1、以下哪项加点词语注音全对？(2分)A、筹办(chóu)。

B、傲慢(ào)。

C、恫吓(tòng)。

D、呐喊(nà)2、以下哪项没有错别字？(2分)A、。

B、淋漓。

C、仰慕。

D、钦佩3、以下哪句没有语病？(2分)A、同学们的热心帮助使他更加坚定了追求美好人生理想的信心。

B、中国人民有信心有能力把自己的国家建设得更加美好。

C、老师的和蔼可亲的笑脸和谆谆教诲总是浮现在我面前。

D、他强壮有力地走向我们。

4、以下哪项加点词语运用有误？(2分)A、同学们在运动场上生龙活虎，来势汹汹。

B、这个人迹罕至的丛林就是鸟儿的天堂。

C、XXX同志的先进事迹已广为流传，家喻户晓。

D、XXX先生义愤填膺，拍案而起，面对特务的嚣张气焰。

5、以下哪句没有语病？(2分)A、2004年中国健儿以优异的成绩从雅典奥运会胜利凯旋归来。

B、在老师的悉心辅导下，我的数学成绩迅速提高了。

C、我不得不承认我确实是做错了。

D、本周治安状况良好，犯罪率较上周下降了一倍。

6、根据上下文连贯的要求，选择最恰当的一项填入横线中。

(2分)黄河，中华民族的母亲河。

五千多年的华夏文明史，与母亲有着血肉相连的关系。

黄河流千古，流出了什么？(漫无边际的黄土地/灿若明珠的黄河古文化/黄皮肤的群落)7、仿写：(2分)2015年的期末考试，对于我们来说是一次重要的考验。

我们需要充分利用平时的时间，积累知识，提高能力。

只有这样，我们才能在考试中取得好成绩。

Animal is the partner of human survival。

With them。

the world is so diverse and vibrant。

and they give XXX to use their lives to open up a path for the next n when the pXXX。

2015年七年级下册数学期末试卷(附答案)一、选择题：(本大题共10个小题，每小题3分，共30分) 1．若m ＞－1，则下列各式中错误的．．．是（ ） A ．6m ＞－6 B ．－5m ＜－5 C ．m+1＞0 D ．1－m ＜22. 线段CD 是由线段AB 平移得到的，点A （-1，4）的对应点为C （4，7），则点B （-4，-1）•的对应点的坐标为（ ）（A ）（2，9） （B ）（5，3） （C ）（1，2） （D ）（-9，-4） 3．已知a ＞b ＞0，那么下列不等式组中无解．．的是（ ） A ．⎩⎨⎧-><b x a x B ．⎩⎨⎧-<->b x a x C ．⎩⎨⎧-<>b x a x D ．⎩⎨⎧<->b x ax4．一辆汽车在公路上行驶，两次拐弯后，仍在原来的方向上平行行驶，那么两个拐弯的角度可能为 （ ）(A) 先右转50°，后右转40° (B) 先右转50°，后左转40° (C) 先右转50°，后左转130° (D) 先右转50°，后左转50° 5．解为12x y =⎧⎨=⎩的方程组是（ ）A.135x y x y -=⎧⎨+=⎩B.135x y x y -=-⎧⎨+=-⎩C.331x y x y -=⎧⎨-=⎩D.2335x y x y -=-⎧⎨+=⎩6．如图，在△ABC 中，∠ABC=500，∠ACB=800，BP 平分∠ABC ，CP 平分∠ACB ，则∠BPC 的大小是（ ）A ．1000B ．1100C ．1150D ．120PBA(1) (2) (3)7．四条线段的长分别为3，4，5，7，则它们首尾相连可以组成不同的三角形的个数是（ ） A ．4 B ．3 C ．2 D ．18．在各个内角都相等的多边形中，一个外角等于一个内角的12，则这个多边形的边数是（ ）A ．5B ．6C ．7D ．8 9．如图，△A 1B 1C 1是由△ABC 沿BC 方向平移了BC 长度的一半得到的，若△ABC 的面积为20 cm 2，则四边形A 1DCC 1的面积为（ ）A ．10 cm 2B ．12 c m 2C ．15 cm 2D ．17 cm 210.课间操时,小华、小军、小刚的位置如图1,小华对小刚说,如果我的位置用(•0,0)表示,小军的位置用(2,1)表示,那么你的位置可以表示成( )C 1A 1二、填空题：本大题共8个小题，每小题3分，共24分，把答案直接填在答题卷的横线上． 11.一个多边形的每一个内角都是140°， •它是________边形． 12.不等式5x-9≤3(x+1)的解集是________. 13.如果点P(a,2)在第二象限,那么点Q(-3,a)在_______.14.如图3所示,在铁路旁边有一李庄,现要建一火车站,•为了使李庄人乘火车最方便(即距离最近),请你在铁路旁选一点来建火车站(位置已选好),说明理由:____________.15.从A 沿北偏东60°的方向行驶到B,再从B 沿南偏西20°的方向行驶到C,•则∠ABC=_______度.16.如图,AD ∥BC,∠D=100°,CA 平分∠BCD,则∠DAC=_______.17．给出下列正多边形：① 正三角形；② 正方形；③ 正六边形；④ 正八边形．用上述正多边形中的一种能够辅满地面的是_____________．(将所有答案的序号都填上) 18. 若方程组234,3223x y x y m +=⎧⎨+=-⎩的解满足x+y=15，则m=______．三、解答题：本大题共7个小题，共46分，解答题应写出文字说明、证明过程或演算步骤．19．解不等式组：⎪⎩⎪⎨⎧+<-≥--.21512,4)2(3x x x x ,并把解集在数轴上表示出来．20．解方程组：2313424()3(2)17x y x y x y ⎧-=⎪⎨⎪--+=⎩CB A D21.如图, AD ∥BC , AD 平分∠EAC,你能确定∠B 与∠C 的数量关系吗?请说明理由。

2015七年级数学第二学期期末测试（最新版 人教）一、选择题（本大题共12小题，每小题3分，共36分．在每小题给出的的四个选项中，只有一项是正确的，请用2B 铅笔把答题卷上对应题目的答案涂黑） 1．下列四种说法中正确的是（ ）．A ．连结两点间的线段叫两点间的距离B ．射线AB 与射线BA 是同一条射线C ．相等的角是对顶角D ．若直线a ∥b ，b ∥c ，则a ∥c2．如图，一把矩形直尺沿直线断开并错位，点E 、D 、B 、F 在同一条直线上，若∠ADE ＝125°, 则∠DBC 的度数为（ ）．A ．55°B ．65°C ．75°D ．125°3．下列图中，12∠∠与属于对顶角的是（ ）．4．已知关于x 的不等式组恰有3个整数解，则a 的取值范围是（ ）A ．B ．C ．D ．5．14年株洲市，8，3分)在平面直角坐标系中，孔明做走棋的游戏，其走法是：棋子从原点出发，第1步向右走1个单位，第2步向右走2个单位，第3步向上走1个单位，第4步向右走1个单位……，依此类推，第n 步的走法是；当n 能被3整除时，则向上走1个单位：当n 被3除，余数为1时，则向右走1个单位；当n 被3整除，余数为2时，则向右走2个单位。

当走完第100步时，棋子所处位置的坐标是（ ） A ．（66,34） B ．（67,33） C ．（100,33）D ．（99,34） 6．下列等式正确的是（） .......................................A 34± B113 C ：393-=- D 13 7．下列调查方式中，合适的是（ ）．A ．调查你所在班级同学的身高，采用抽样调查的方式．B ．要了解外地游客对恭城旅游景点“孔庙”的满意程度，采用抽样调查的方式．C ．要保证“神舟七号”飞船成功发射，对主要零部件的检查采用抽样调查的方式．D ．要了解全灌阳县初中学生的业余爱好，采用普查的方式． 8． 下列说法中正确的是（ ）A 、若a 为实数，则0≥aB 、若a 为实数，则a 的倒数为a1C 、若y x 、为实数，且y x =，则y x =D 、若a 为实数，则02≥a9．如果关于x 的不等式()20112011+>+a x a 的解集为1<x ，那么a 的取值范围是（ ）．A ．2011->aB ．2011-<aC ．2011>aD ．2011<aABCD121212 1210．在实数：231169,(),0.326,(0.5),ππ⋯,0.1030030003,--x 个，有理数有y 个，非负数有z 个，则x ＋y ＋z 等于（ ） A ：12 B ：13 C ：14 D ：1511．(2013湖北荆门，9，3分)若关于x 的一元一次不等式组20,2x m x m -<⎧⎨+>⎩有解，则m 的取值范围为( )A ．m ＞－23 B ．m ≤23 C ．m ＞23 D ．m ≤－2312．．四个电子宠物排座位，一开始，小鼠、小猴、小兔、小猫分别坐在1、2、3、4号座位上（如图所示），以后它们不停地变换位置，第一次上下两排交换，第二次是在第一次换位后，再左右两列交换位置，第三次上下两排交换，第四次再左右两列交换……这样一直下去，则第2011次交换位置后，小兔子坐在（ ）号位上．4321猫兔猴鼠猫兔猴鼠猫兔猴鼠→→…A ．1B ．2C ．3D ．413．如图是一块长方形ABCD 的场地，长AB =102m ，宽AD =51m ，从A 、B 两处入口的中路宽都为1m ，两小路汇合处路宽为2m ，其余部分种植草坪，则草坪面积为（ ）（A ）5050m 2 （B ）4900m 2 （Ｃ）5000m 2（Ｄ）4998m 2二、填空题（本大题共6小题，每小题3分，共18分）请将答案填在答题卷上.14．命题“同位角相等，两直线平行”中，题设是 ，结论是 ． 15．若不等式组的解集是﹣1＜x ＜1，则（a +b ）2009= ．16．计算：3200989)1(+-- =___________ 17请你将发现的规律用含自然数n(n ≥1)的等式表示出来 ．18．若1.1001.102=，则=±0201.1 19．三个同学对问题“若方程组111222a x b y c a x b y c +=⎧⎨+=⎩的解是34x y =⎧⎨=⎩，求方程组111222325325a x b y c a x b y c +=⎧⎨+=⎩的解．”提出各自的想法．甲说：“这个题目好象条件不够，不能求解”；乙说：“它们的系数有一定的规律，可以试试”；丙说：“能不能把第二个方程组的两个方程的两边都除以5，通过换元替代的方法来解决”．参考他们的讨论，你认为这个题目的解应该是 ．20．观察下列由棱长为1的小立方体摆成的图形，寻找规律：如图1中：共有1 个小立方体，其中1个看得见，0A SB S个看不见；如图2中：共有8个小立方体，其中7个看得见，1个看不见；如图3中：共有27个小立方体，其中有19个看得见，8个看不见；……，则第6个图中，看不见的小立方体有 个。

2015年初一第二学期数学期末试卷（带答案）距离期末考试还有不到一个月的时间了，在这段时间内突击做一些试题是非常有帮助的，下文整理了2015年初一第二学期数学期末试卷，希望对大家有所帮助!预祝大家取得好成绩! 一、选择题(每题3分，共30分) 1.点P(2，-3)所在象限为( ) A、第一象限 B、第二象限 C、第三象限 D、第四象限 2.当a大于b时，下列各式中不正确的是( ) A、a-3大于b-3 B、3-a小于3-b C、 D、 3.点A(-3，-5)向上平移4个单位,再向左平移3个单位到点B，则点B的坐标为( ) A、(1,-8) B、(1, -2) C、(-7,-1 ) D、( 0,-1) 4.如右图，下列能判定∥的条件有( )个. (1) (2) ;(3) ;(4) . A.1 B.2 C.3 D.4 5.在直角坐标系中，点P(6-2x，x-5)在第四象限， 则x的取值范围是( ). A、3 6.如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，则&ang;A与&ang;1+&ang;2之间有一种数量关系始终保持不变.请试着找一找这个规律，你发现的规律是( ) A.&ang;A=&ang;1+&ang;2 B.2&ang;A=&ang;1+&ang;2 C.3&ang;A=2&ang;1+&ang;2 D.3&ang;A=2(&ang;1+&ang;2) 7.已知五个命题，正确的有( ) (1)有理数与无理数之和是无理数⑵有理数与无理数之积是无理数 (3)无理数与无理数之积是无理数⑷无理数与无理数之积是有理数 (5)所有的有理数都可以在数轴上表示，反过来，数轴上所有的点都表示有理数。

 A. 1个B. 2个C. 3个D.4个 8.为了了解参加某运动会的2000名运动员的年龄情况，从中抽取了100名运动员的年龄，就这个问题来说，下面说法正确的是( ). A.2000名运动员是总体B.100名运动员是所抽取的一个样本 C.样本容量为100名D.抽取的100名运动员的年龄是样本 9.若是49的算术平方根，则= ( ) A. 7 B. -7 C. 49 D.-49 10. 如右图，，且&ang;A=25度，&ang;C=45度，则&ang;E的度数是( ) A. B. C. D. 二、填空题(每题3分，共24分) 11.点P在第二象限，P到x轴的距离为4，P到y轴距离为3，则点P的坐标为(　，　) 12. 的算术平方根是_____. 13.若不等式组解集为x大于2，则的取值范围是. 14. 两根木棒的长分别为和.要选择第三根木棒，将它们钉成一个三角形框架，那幺，第三根木棒长( )的范围是____________. 15. 在自然数范围内,方程x+3y=10的解是____ ___. 16. 下列各数中，有理数为;无理数为 (相邻两个3之间的7逐渐加1个) 17. 小陈从O点出发，前进5米后向右转20度，再前进5米后又向右转20度，，这样一直走下去，他第一次回到出发点O时一共走了_________. 18、为了估计池塘里有多少条鱼，先从湖里捕捞100条鱼坐上标记，然后放回池塘去，经过一段时间，待有有标记的鱼完全混合于鱼群后，第二次再捕捞100条鱼，发现有5条有标记，那幺你估计池塘里有多少条鱼 三、解下列各题(共76分) 19. (每题6分)(1)计算 (2) 解方程组 (3))解不等式组并把不等式组的解集在数轴上表示出来 20 完成下面的解题过程，并在括号内填上依据。

人教版七年级下册数学期末试卷(1)一、选择题（答案填入下表中，每小题3分，共30分)1、在平面直角坐标系中,点P（－3，4）位于（）A、第一象限B、第二象限C、第三象限D、第四象限2、为了了解全校七年级300名学生的视力情况，骆老师从中抽查了50名学生的视力情况、针对这个问题，下面说法正确的是( )A、300名学生是总体B、每名学生是个体C、50名学生是所抽取的一个样本D、这个样本容量是503、导火线的燃烧速度为0.8cm/s，爆破员点燃后跑开的速度为5m/s,为了点火后能够跑到150m外的安全地带，导火线的长度至少是（）A、22cmB、23cmC、24cmD、25cm4、不等式组的解集为,则a满足的条件是( )A、B、C、D、5、下列四个命题：①对顶角相等；②内错角相等；③平行于同一条直线的两条直线互相平行；④如果一个角的两边分别平行于另一个角的两边，那么这两个角相等。

其中真命题的个数是( ）A、1个B、2个C、3个D、4个6、下列运动属于平移的是( ）A、荡秋千B、地球绕着太阳转C、风筝在空中随风飘动D、急刹车时，汽车在地面上的滑动7、一个正方形的面积是15，估计它的边长大小在( ）A、2与3之间B、3与4之间C、4与5之间D、5与6之间8、已知实数,满足,则等于( )A、3B、－3C、1D、－19、如图是丁丁画的一张脸的示意图，如果用（0，2)表示左眼,用(2，2)表示右眼，那么嘴的位置可以表示成（）A、(1,0）B、（－1，0)C、（－1，1）D、(1,－1)10、根据以下对话，可以求得嫒嫒所买的笔和笔记本的价格分别是( ）111213线上；若∠1=40°，则∠2的度数为.14、某初中学校共有学生720人,该校有关部门从全体学生中随机抽取了50人，对其到校方式进行调查，并将调查的结果制成了如图所示的条形统计图,由此可以估计全校坐公交车到校的学生有人。

15、设表示大于的最小整数，如，,则下列结论中正确的是。