湖南省2011年高考数学 必考点题型热点预测与分析(3) 立体几何与空间向量

高考数学考点重点剖析立体几何与空间向量的多重综合应用在高考数学中，立体几何与空间向量是两个重要的考点，而且它们经常在一些综合性的题目中出现。

本文将对立体几何和空间向量进行剖析，并探讨它们在高考中的多重综合应用。

一、立体几何的重点考点分析立体几何是数学中的一个分支，主要研究物体的形状、大小以及它们之间的相互关系。

在高考中，立体几何通常涉及到平行四边形、正方体、圆锥等几何图形的计算与分析。

以下是一些重点考点的剖析：1. 平行四边形的性质与应用平行四边形是立体几何中的一种基本图形，具有一些重要的性质。

例如，对角线互相平分、对边平行、对边长度相等等。

在高考中，平行四边形的应用非常广泛，可以用来解决计算面积、周长以及角度等问题。

2. 正方体的构造与计算正方体是一种非常规则的立体图形，它的六个面都是正方形。

在高考中，经常会出现一些正方体相关的计算题目，例如计算体积、表面积等。

掌握正方体的构造与计算方法对于解题非常有帮助。

3. 圆锥的性质与问题求解圆锥是一种具有锥形的立体图形，它的底面是一个圆。

在高考中，圆锥的性质与问题求解也是一个重要的考点。

比如，计算圆锥的体积、侧面积等。

要想解决这些问题，首先需要了解圆锥的性质与公式。

二、空间向量的重点考点分析空间向量是高考数学中的另一个重要考点。

它关注的是空间中点的位置与运动的方向和距离。

以下是一些空间向量的重点考点剖析：1. 空间向量的定义与性质空间向量的定义是指空间中的两点所确定的有向线段，它具有方向和模长。

在空间向量的定义中，需要了解空间向量的坐标表示、向量加法与减法等基本运算性质。

2. 空间向量的数量积与向量积空间向量的数量积与向量积是空间向量的重要性质。

数量积可以用来计算两个向量的夹角，而向量积可以用来计算两个向量所确定平面的面积。

在高考中，经常会出现一些与数量积和向量积相关的计算题目。

三、立体几何与空间向量的多重综合应用在高考中，立体几何与空间向量往往会在一些综合性的题目中出现，并进行多重综合应用。

高中数学第九章-立体几何考试内容平面及其基本性质．平面图形直观图的画法．平行直线．对应边分别平行的角．异面直线所成的角．异面直线的公垂线．异面直线的距离．直线和平面平行的判定与性质．直线和平面垂直的判定与性质．点到平面的距离．斜线在平面上的射影．直线和平面所成的角．三垂线定理及其逆定理．平行平面的判定与性质．平行平面间的距离．二面角及其平面角．两个平面垂直的判定与性质．多面体．正多面体．棱柱．棱锥．球．考试要求（1）掌握平面的基本性质，会用斜二测的画法画水平放置的平面图形的直观图;能够画出空间两条直线、直线和平面的各种位置关系的图形，能够根据图形想像它们的位置关系．（2）掌握两条直线平行与垂直的判定定理和性质定理，掌握两条直线所成的角和距离的概念，对于异面直线的距离，只要求会计算已给出公垂线时的距离．（3）掌握直线和平面平行的判定定理和性质定理；掌握直线和平面垂直的判定定理和性质定理；掌握斜线在平面上的射影、直线和平面所成的角、直线和平面的距离的概念掌握三垂线定理及其逆定理．（4）掌握两个平面平行的判定定理和性质定理，掌握二面角、二面角的平面角、两个平行平面间的距离的概念，掌握两个平面垂直的判定定理和性质定理．（5）会用反证法证明简单的问题．（6）了解多面体、凸多面体的概念，了解正多面体的概念．（7）了解棱柱的概念，掌握棱柱的性质，会画直棱柱的直观图．（8）了解棱锥的概念，掌握正棱锥的性质，会画正棱锥的直观图．（9）了解球的概念，掌握球的性质，掌握球的表面积、体积公式．9（B）．直线、平面、简单几何体考试内容：平面及其基本性质．平面图形直观图的画法．平行直线．直线和平面平行的判定与性质．直线和平面垂直的判定．三垂线定理及其逆定理．两个平面的位置关系．空间向量及其加法、减法与数乘．空间向量的坐标表示．空间向量的数量积．直线的方向向量．异面直线所成的角．异面直线的公垂线．异面直线的距离．直线和平面垂直的性质．平面的法向量．点到平面的距离．直线和平面所成的角．向量在平面内的射影．平行平面的判定和性质．平行平面间的距离．二面角及其平面角．两个平面垂直的判定和性质．多面体．正多面体．棱柱．棱锥．球．考试要求：（1）掌握平面的基本性质。

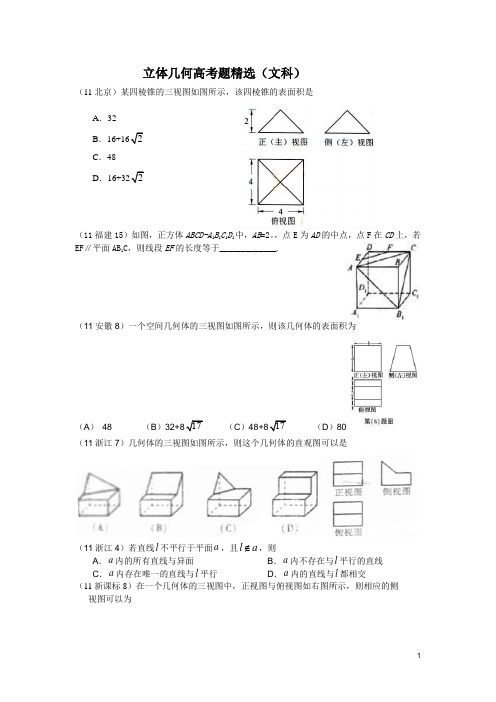
立体几何高考题精选（文科）（11北京）某四棱锥的三视图如图所示，该四棱锥的表面积是A．32B．C．48D．（11福建15）如图，正方体ABCD-A1B1C1D1中，AB=2。

，点E为AD的中点，点F在CD上，若EF∥平面AB1C，则线段EF的长度等于_____________.（11安徽8）一个空间几何体的三视图如图所示，则该几何体的表面积为（A）48 （B）（C）（D）80（11浙江7）几何体的三视图如图所示，则这个几何体的直观图可以是∉，则（11浙江4）若直线l不平行于平面a，且l aA．a内的所有直线与异面B．a内不存在与l平行的直线C．a内存在唯一的直线与l平行D．a内的直线与l都相交（11新课标8）在一个几何体的三视图中，正视图与俯视图如右图所示，则相应的侧视图可以为(11天津10)一个几何体的三视图如图所示（单位：m ），则该几何体的体积为__________3m（11四川6）1l ，2l ，3l 是空间三条不同的直线，则下列命题正确的是（A ）12l l ⊥，23l l ⊥13//l l ⇒（B ）12l l ⊥，23//l l ⇒13l l ⊥（C ）233////l l l ⇒1l ，2l ，3l 共面（D ）1l ，2l ，3l 共点⇒1l ，2l ，3l 共面（11上海7）若一个圆锥的主视图（如图所示）是边长为3,3,2的三角形，则该圆锥的侧面积是 。

（11陕西5）某几何体的三视图如图所示，则它的体积是【】 (A)283π- (B)83π-(C)8-2π (D)23π（11山东11）下图是长和宽分别相等的两个矩形．给定下列三个命题：①存在三棱柱，其正（主）视图、俯视图如下图；②存在四棱柱，其正（主）视图、俯视图如下图；③存在圆柱，其正（主）视图、俯视图如下图．其中真命 题的个数是 A ．3 B ．2C ．1D ．0(11全国8) 已知直二面角l αβ--，点A ∈α，AC l ⊥,C 为垂足，点B ∈β，BD l ⊥,D 为垂足.若AB =2，AC =BD =1，则CD =（A ） 2 （B（C（D ）1(11全国12) 已知平面α截一球面得圆M ，过圆心M 且与α成060二面角的平面β截该球面得圆N.若该球面的半径为4，圆M 的面积为4π，则圆N 的面积为 (A)7π (B)9π (C)11π (D)13π（11全国15）已知正方体ABCD-A 1B 1C 1D 1中，E 为C 1D 1的中点，则异面直线AE 与BC 所成角的余弦值为 .（11辽宁8）一个正三棱柱的侧棱长和底面边长相等，体积为32，它的三视图中的俯视图如右图所示，左视图是一个矩形，则这个矩形的面积是A ．4B ．32C ．2D ．3（11辽宁10）已知球的直径SC=4，A ，B 是该球球面上的两点，AB=2，∠ASC=∠BSC=45°，则棱锥S-ABC 的体积为ABCD（11江西）将长方体截去一个四棱锥，得到的几何体如右图所示，则该几何体的左视图为（ ）（11湖南）设图１是某几何体的三视图，则该几何体的体积为A ．942π+Ｂ．3618π+ Ｃ．9122π+ Ｄ．9182π+正视图侧视图（11湖北）设球的体积为V ，它的内接正方体的体积为V ，下列说法中最合适的是A. V 比V 大约多一半B. V 比V 大约多两倍半C. V 比V大约多一倍D. V 比V大约多一杯半（11广东）正五棱柱中，不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线，那么一个正五棱柱对角线的条数共有 A ．20 B ．15 C ．12 D ．10 （11广东9）如图1-3，某几何体的正视图（主视图），侧视图（左视图）和俯视图分别是等腰三角形和菱形，则该几何体体积为A ．34B ．4C ．32D ．2（11北京17）如图，在四面体PABC 中，PC ⊥AB ，PA ⊥BC,点D,E,F,G 分别是棱AP,AC,BC,PB的中点.（Ⅰ）求证：DE ∥平面BCP ；（Ⅱ）求证：四边形DEFG 为矩形； （Ⅲ）是否存在点Q ，到四面体PABC 六条棱的中点的距离相等？说明理由.（11福建20）（本小题满分12分）如图，四棱锥P-ABCD 中，P A ⊥底面ABCD ，AB ⊥AD ，点E 在线段AD 上，且CE ∥AB 。

专题四：立体几何第三讲 空间向量与立体几何【最新考纲透析】1．空间向量及其运算（1）了解空间向量的概念，了解空间向量的基本定理及其意义，掌握空间向量的线性运算及其坐标表示。

（2）掌握空间向量的线性运算及其坐标表示。

（3）掌握空间向量的数量积及其坐标表示，能运用向量的数量积判断向量的共线与垂直。

2．空间向量的应用（1）理解直线的方向向量与平面的法向量。

（2）能用向量语言表述直线与直线，直线与平面，平面与平面的垂直、平行关系。

（3）能用向量方法证明有关直线和平面位置关系的一些定理（包括三垂线定理）。

（4）能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题，了解向量方法在研究立体几何问题中的应用。

【核心要点突破】要点考向1：利用空间向量证明空间位置关系考情聚焦：1．平行与垂直是空间关系中最重要的位置关系，也是每年的必考内容，利用空间向量判断空间位置关系更是近几年高考题的新亮点。

2．题型灵活多样，难度为中档题，且常考常新。

考向链接：1．空间中线面的平行与垂直是立体几何中经常考查的一个重要内容，一方面考查学生的空间想象能力和逻辑推理能力；另一个方面考查“向量法”的应用。

2．空间中线面的平行与垂直的证明有两个思路：一是利用相应的判定定理和性质定理去解决；二是利用空间向量来论证。

例1：（2010·安徽高考理科·Ｔ18）如图，在多面体ABCDEF 中，四边形ABCD 是正方形，EF ∥AB ，EF FB ⊥，2AB EF =，90BFC ∠=︒，BF FC =，H 为BC 的中点。

(1)求证：FH ∥平面EDB ；(2)求证：AC ⊥平面EDB ； (3)求二面角B DE C --的大小。

【命题立意】本题主要考查了空间几何体的线面平行、线面垂直的证明、二面角的求解的问题，考查了考生的空间想象能力、推理论证能力和运算求解能力。

【思路点拨】可以采用综合法证明，亦可采用向量法证明。

高中数学立体几何经典常考题型题型一:空间点、线、面的位置关系及空间角的计算空间点、线、面的位置关系通常考查平行、垂直关系的证明，一般出现在解答题的第(1)问，解答题的第(2)问常考查求空间角，求空间角一般都可以建立空间直角坐标系，用空间向量的坐标运算求解.【例1】如图，在△ABC中，∠ABC＝，O为AB边上一点，且3OB＝3OC＝2AB，已知PO⊥平面ABC，2DA＝2AO＝PO，且DA∥PO.(1)求证：平面PBD⊥平面COD；(2)求直线PD与平面BDC所成角的正弦值.(1)证明　∵OB＝OC，又∵∠ABC＝，∴∠OCB＝，∴∠BOC＝.⊥∴CO AB.又PO⊥平面ABC，⊥OC⊂平面ABC，∴PO OC.又∵PO，AB⊂平面PAB，PO∩AB＝O，∴CO⊥平面PAB，即CO⊥平面PDB.又CO⊂平面COD，∴平面PDB⊥平面COD.(2)解　以OC，OB，OP所在射线分别为x，y，z轴，建立空间直角坐标系，如图所示.设OA＝1，则PO＝OB＝OC＝2，DA＝1.则C(2，0，0)，B(0，2，0)，P(0，0，2)，D(0，－1，1)，∴PD＝(0，－1，－1)，BC＝(2，－2，0)，BD＝(0，－3，1).设平面BDC的一个法向量为n＝(x，y，z)，∴∴令y＝1，则x＝1，z＝3，∴n＝(1，1，3).设PD与平面BDC所成的角为θ，则sin θ＝＝＝.即直线PD与平面BDC所成角的正弦值为.【类题通法】利用向量求空间角的步骤间标.第一步：建立空直角坐系第二步：确定点的坐标.线)坐标.第三步：求向量(直的方向向量、平面的法向量计夹(或函数值).第四步：算向量的角将夹转为间.第五步：向量角化所求的空角查关键错题规.第六步：反思回顾.看点、易点和答范【变式训练】 如图所示，在多面体A1B1D1DCBA中，四边形AA1B1B，ADD1A1，ABCD均为正方形，E为B1D1的中点，过A1，D，E的平面交CD1于F.(1)证明：EF∥B1C.(2)求二面角EA1DB1的余弦值.(1)证明　由正方形的性质可知A1B1AB DC∥∥，且A1B1＝AB＝DC，所以四边形A1B1CD为平行四边形，从而B1C A∥1D，又A1D⊂面A1DE，B1C⊄面A1DE，于是B1C∥面A1DE.又B1C⊂面B1CD1，面A1DE∩面B1CD1＝EF，所以EF∥B1C.(2)解　因为四边形AA1B1B，ADD1A1，ABCD均为正方形，所以AA1⊥AB，AA1⊥AD，AB⊥AD且AA1＝AB＝AD.以A为原点，分别以AB，AD，AA1为x轴，y轴和z轴单位正向量建立如图所示的空间直角坐标系，可得点的坐标A(0，0，0)，B(1，0，0)，D(0，1，0)，A1(0，0，1)，B1(1，0，1)，D1(0，1，1)，而E点为B1D1的中点，所以E点的坐标为.设平面A1DE的一个法向量n1＝(r1，s1，t1)，而该面上向量A1E＝，A1D＝(0，1，－1)，由n1⊥A1E，n1⊥A1D得r1，s1，t1应满足的方程组(－1，1，1)为其一组解，所以可取n1＝(－1，1，1).设平面A1B1CD的一个法向量n2＝(r2，s2，t2)，而该面上向量A1B1＝(1，0，0)，A1D＝(0，1，－1)，由此同理可得n2＝(0，1，1).所以结合图形知二面角EA1DB1的余弦值为＝＝.题型二:立体几何中的探索性问题此类试题一般以解答题形式呈现，常涉及线、面平行、垂直位置关系的探究或空间角的计算问题，是高考命题的热点，一般有两种解决方式：(1)根据条件作出判断，再进一步论证；(2)利用空间向量，先假设存在点的坐标，再根据条件判断该点的坐标是否存在.【例2】如图，在四棱锥P－ABCD中，平面PAD⊥平面ABCD，PA⊥PD，PA＝PD，AB⊥AD，AB＝1，AD＝2，AC＝CD＝.(1)求证：PD⊥平面PAB；(2)求直线PB与平面PCD所成角的正弦值；(3)在棱PA上是否存在点M，使得BM∥平面PCD？若存在，求的值；若不存在，说明理由.(1)证明　因为平面PAD⊥平面ABCD，平面PAD∩平面ABCD＝AD，AB⊥AD，所以AB⊥平面PAD，所以AB⊥PD.又PA⊥PD，AB∩PA＝A，所以PD⊥平面PAB.(2)解　取AD的中点O，连接PO，CO.因为PA＝PD，所以PO⊥AD.因为PO⊂平面PAD，平面PAD⊥平面ABCD，所以PO⊥平面ABCD.因为CO⊂平面ABCD，所以PO⊥CO.因为AC＝CD，所以CO⊥AD.如图，建立空间直角坐标系O－xyz.由题意得，A(0，1，0)，B(1，1，0)，C(2，0，0)，D(0，－1，0)，P(0，0，1).设平面PCD的一个法向量为n＝(x，y，z)，则即令z＝2，则x＝1，y＝－2.所以n＝(1，－2，2).又PB＝(1，1，－1)，所以cos〈n，PB〉＝＝－.所以直线PB与平面PCD所成角的正弦值为.(3)解　设M是棱P A上一点，则存在λ∈0，1]，使得AM＝λAP.因此点M(0，1－λ，λ)，BM＝(－1，－λ，λ).因为BM⊄平面PCD，所以要使BM∥平面PCD，则BM·n＝0，即(－1，－λ，λ)·(1，－2，2)＝0，解得λ＝.所以在棱P A上存在点M，使得BM∥平面PCD，此时＝.应设，把要成立的作件结论当条，据此列方对断问题，先假存在【类题通法】(1)于存在判型的求解规围内”等.标，是否有定范的解程或方程组，把“是否存在”化问题转为“点的坐是否有解对问题，通常借助向量，引进参数，合已知和列出等式综结论，解出参数.(2)于位置探究型【变式训练】如图，在四棱锥P－ABCD中，PD⊥平面ABCD，AB∥DC，AB⊥AD，DC＝6，AD＝8，BC＝10，∠P AD＝45°，E为P A的中点.(1)求证：DE∥平面BPC；(2)线段AB上是否存在一点F，满足CF⊥DB？若存在，试求出二面角F－PC－D的余弦值；若不存在，请说明理由.(1)证明　取PB的中点M，连接EM和CM，过点C作CN⊥AB，垂足为点N.∵CN⊥AB，DA⊥AB，∴CN∥DA，又AB∥CD，∴四边形CDAN为平行四边形，∴CN＝AD＝8，DC＝AN＝6，在Rt△BNC中，BN＝＝＝6，∴AB＝12，而E，M分别为P A，PB的中点，∴EM∥AB且EM＝6，又DC∥AB，∥且EM＝CD，四边形CDEM为平行四边形，∴EM CD∥∵⊂平面PBC，DE⊄平面PBC，∴DE CM.CM∴DE∥平面BPC.(2)解　由题意可得DA，DC，DP两两互相垂直，如图，以D为原点，DA，DC，DP分别为x，y，z轴建立空间直角坐标系D－xyz，则A(8，0，0)，B(8，12，0)，C(0，6，0)，P(0，0，8).假设AB上存在一点F使CF⊥BD，设点F坐标为(8，t，0)，则CF＝(8，t－6，0)，DB＝(8，12，0)，由CF·DB＝0得t＝.又平面DPC的一个法向量为m＝(1，0，0)，设平面FPC的法向量为n＝(x，y，z).又PC＝(0，6，－8)，FC＝.由得即不妨令y＝12，有n＝(8，12，9).则cos〈n，m〉＝＝＝.又由图可知，该二面角为锐二面角，故二面角F－PC－D的余弦值为.题型三:立体几何中的折叠问题将平面图形沿其中一条或几条线段折起，使其成为空间图形，这类问题称为立体几何中的折叠问题，折叠问题常与空间中的平行、垂直以及空间角相结合命题，考查学生的空间想象力和分析问题的能力.【例3】如图，菱形ABCD的对角线AC与BD交于点O，AB＝5，AC＝6，点E，F分别在AD，CD 上，AE＝CF＝，EF交BD于点H.将△DEF沿EF折到△D′EF的位置，OD′＝.(1)证明：D′H⊥平面ABCD；(2)求二面角B－D′A－C的正弦值.(1)证明　由已知得AC ⊥BD ，AD ＝CD .又由AE ＝CF 得＝，故AC ∥EF .因此EF ⊥HD ，从而EF ⊥D ′H .由AB ＝5，AC ＝6得DO ＝BO ＝＝4.由EF ∥AC 得＝＝.所以OH ＝1，D ′H ＝DH ＝3.于是D ′H 2＋OH 2＝32＋12＝10＝D ′O 2，故D ′H ⊥OH .又D ′H ⊥EF ，而OH ∩EF ＝H ，所以D ′H ⊥平面ABCD .(2)解　如图，以H 为坐标原点，HF 的方向为x 轴正方向，建立空间直角坐标系H －xyz .则H (0，0，0)，A (－3，－1，0)，B (0，－5，0)，C (3，－1，0)，D ′(0，0，3)，AB ＝(3，－4，0)，AC ＝(6，0，0)，AD′＝(3，1，3).设m ＝(x 1，y 1，z 1)是平面ABD ′的一个法向量，则即所以可取m ＝(4，3，－5).设n ＝(x 2，y 2，z 2)是平面ACD ′的一个法向量，则即所以可取n ＝(0，－3，1).于是cos 〈m ，n 〉＝＝＝－.sin 〈m ，n 〉＝.因此二面角B －D ′A －C 的正弦值是.【类题通法】立体几何中的折叠问题，是翻折前后形中面位置系和度量系的化关键搞清图线关关变情况，一般地翻折后在同一平面上的性不生化还个质发变，不在同一平面上的性生化个质发变.【变式训练】如图1，在直角梯形ABCD 中，AD ∥BC ，∠BAD ＝，AB ＝BC ＝1，AD ＝2，E 是AD 的中点，O 是AC 与BE 的交点.将△ABE 沿BE 折起到△A 1BE 的位置，如图2.(1)证明：CD⊥平面A1OC；(2)若平面A1BE⊥平面BCDE，求平面A1BC与平面A1CD夹角的余弦值.(1)证明　在题图1中，因为AB＝BC＝1，AD＝2，E是AD的中点，∠BAD＝，所以BE⊥AC.即在题图2中，BE⊥OA1，BE⊥OC，从而BE⊥平面A1OC.又CD∥BE，所以CD⊥平面A1OC.(2)解　由已知，平面A1BE⊥平面BCDE，又由(1)知，BE⊥OA1，BE⊥OC，所以∠A1OC为二面角A1－BE－C的平面角，所以∠A1OC＝.如图，以O为原点，OB，OC，OA1分别为x轴、y轴、z轴正方向建立空间直角坐标系，因为A1B＝A1E＝BC＝ED＝1，BC∥ED，所以B，E，A1，C，得BC＝，A1C＝，CD＝BE＝(－，0，0).设平面A1BC的一个法向量n1＝(x1，y1，z1)，平面A1CD的一个法向量n2＝(x2，y2，z2)，平面A1BC与平面A1CD的夹角为θ，则得取n1＝(1，1，1)；得取n2＝(0，1，1)，从而cos θ＝|cos〈n1，n2〉|＝＝，即平面A1BC与平面A1CD夹角的余弦值为.。

立体几何与空间向量03 空间点、线、面的位置关系一、具体目标：1.理解空间直线、平面位置关系的定义，并了解可以作为推理依据的公理和定理；2.以立体几何的定义、公理和定理为出发点，认识和理解空间中线面平行、垂直的有关性质与判定定理；3.能运用公理、定理和已获得的结论证明一些空间位置关系的简单命题.二、知识概述：1.平面的基本性质(1)公理1：如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在这个平面内(即直线在平面内)．(2)公理2：经过不在同一条直线上的三点，有且只有一个平面(即可以确定一个平面)．(3)公理3：如果两个不重合的平面有一个公共点，那么它们有且只有一条通过这个点的公共直线． 推论1：经过一条直线和这条直线外一点，有且只有一个平面．推论2：经过两条相交直线，有且只有一个平面．推论3：经过两条平行直线，有且只有一个平面．2. 空间两直线的位置关系直线与直线的位置关系的分类⎩⎨⎧ 共面直线⎩⎪⎨⎪⎧ 平行相交异面直线：不同在任何一个平面内直线与平面的位置关系有平行、相交、在平面内三种情况．平面与平面的位置关系有平行、相交两种情况．平行公理：平行于同一条直线的两条直线互相平行．等角定理：空间中如果两个角的两边分别对应平行，那么这两个角相等或互补．3.异面直线所成的角①定义：设a ，b 是两条异面直线，经过空间任一点O 作直线a ′∥a ，b ′∥b ，把a ′与b ′所成的锐角或直角叫作异面直线a ，b 所成的角(或夹角)．②范围：.4.异面直线的判定方法： ]2,0(π【考点讲解】判定定理：平面外一点A与平面内一点B的连线和平面内不经过该点的直线是异面直线；反证法：证明两线不可能平行、相交或证明两线不可能共面，从而可得两线异面．5.求异面直线所成的角常采用“平移线段法”，平移的方法一般有三种类型：利用图中已有的平行线平移；利用特殊点(线段的端点或中点)作平行线平移；补形平移．计算异面直线所成的角通常放在三角形中进行．平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面问题化归为共面问题来解决，具体步骤如下：①平移：平移异面直线中的一条或两条，作出异面直线所成的角；②认定：证明作出的角就是所求异面直线所成的角；③计算：求该角的值，常利用解三角形；④取舍：由异面直线所成的角的取值范围是，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．求异面直线所成的角要特别注意异面直线之间所成角的范围．【温馨提示】平面的基本性质，点、直线、平面之间的位置关系是高考试题主要考查知识点，题型除了选择题或填空题外，往往在大题中结合平行关系、垂直关系或角的计算间接考查．1.【2019年高考全国Ⅲ卷】如图，点N为正方形ABCD的中心，△ECD为正三角形，平面ECD⊥平面ABCD，M是线段ED的中点，则（）A．BM=EN，且直线BM，EN是相交直线B．BM≠EN，且直线BM，EN是相交直线C．BM=EN，且直线BM，EN是异面直线D．BM≠EN，且直线BM，EN是异面直线【解析】本题主要考查的空间两条直线的位置关系问题，要求会构造三角形，讨论两直线是否共面，并通过相应的计算确定两条直线的大小关系.如图所示，作EO CD⊥于O，连接ON，BD，易得直线BM，EN是三角形EBD的中线，是相交直线.过M作MF OD⊥于F，连接BF，Q平面CDE⊥平面ABCD，,EO CD EO⊥⊂平面CDE，EO∴⊥平面ABCD，MF⊥平面ABCD，MFB∴△与EON△均为直角三角形．设正方形边长为2，易知12EO ON EN===,，5,2MF BF BM==∴=，BM EN∴≠，故选B．] 2 ,0(π【真题分析】【答案】B2.【2018年高考全国Ⅱ卷理数】在长方体1111ABCD A B C D -中，1AB BC ==，1AA =1AD 与1DB 所成角的余弦值为（ ）A ．15 BCD【解析】方法一：用一个与原长方体相同的长方体拼到原长方体的前面，如图，则11B P AD ∥，连接DP ，易求得1DB DP =，12B P =，则1DB P ∠是异面直线1AD 与1DB 所成的角，由余弦定理可得22211111cos 2DB B P DP DB P DB PB +-∠===⋅.故选C.方法二：以D 为坐标原点，DA ,DC ,DD 1所在直线分别为x ,y ,z 轴建立空间直角坐标系，则()()((110,0,0,1,0,0,,D A B D ,所以((11,AD DB =-=u u u u r u u u u r ,因为111111cos ,5AD DB AD DB AD DB ⋅===u u u u r u u u u r u u u u r u u u u r u u u u r u u u u r ， 所以异面直线1AD 与1DB所成角的余弦值为5，故选C. 【答案】C3. 【2018年高考全国Ⅱ卷文数】在正方体1111ABCD A B C D -中，E 为棱1CC 的中点，则异面直线AE 与CD 所成角的正切值为（ ）A．2 BCD【解析】如图，在正方体1111ABCD A B C D -中，CD AB ∥，所以异面直线AE 与CD 所成角为EAB ∠，设正方体边长为2a ，则由E 为棱1CC 的中点，可得CE a =，所以BE =，则tan BE EAB AB ∠===．故选C ．【答案】C4.【2017年高考全国Ⅱ卷理数】已知直三棱柱111ABC A B C -中，120ABC ∠=︒，2AB =，11BC CC ==，则异面直线1AB 与1BC 所成角的余弦值为（ ）A．2 B．5 C．5D．3 【解析】如图所示，补成直四棱柱1111ABCD A B C D -，则所求角为1111,BC D BC BD C D AB ∠=====Q易得22211C D BD BC =+，因此111cos 5BC BC D C D ∠===，故选C ． 【答案】C5.【2017年高考全国Ⅲ卷文数】在正方体1111ABCD A B C D -中，E 为棱CD 的中点，则（ ）A ．11A E DC ⊥B ．1A E BD ⊥C ．11A E BC ⊥D ．1AE AC ⊥【解析】根据三垂线定理的逆定理，可知平面内的线垂直于平面的斜线，则也垂直于斜线在平面内的射影.A.若11A E DC ⊥，那么11D E DC ⊥，很显然不成立；B.若1A E BD ⊥，那么BD AE ⊥，显然不成立；C.若11A E BC ⊥，那么11BC B C ⊥，成立，反过来11BC B C ⊥时，也能推出11BC A E ⊥,所以C 成立；D.若1A E AC ⊥，则AE AC ⊥，显然不成立，故选C.【答案】C6.【2019年高考北京卷理数】已知l ，m 是平面α外的两条不同直线．给出下列三个论断：①l ⊥m ； ②m ∥α； ③l ⊥α．以其中的两个论断作为条件，余下的一个论断作为结论，写出一个正确的命题：__________．【解析】将所给论断，分别作为条件、结论，得到如下三个命题：（1）如果l ⊥α，m ∥α，则l ⊥m ，正确；（2）如果l ⊥α，l ⊥m ，则m ∥α，不正确，有可能m 在平面α内；（3）如果l ⊥m ，m ∥α，则l ⊥α，不正确，有可能l 与α斜交、l ∥α.故答案为：如果l ⊥α，m ∥α，则l ⊥m.【答案】如果l ⊥α，m ∥α，则l ⊥m .7.【2017年高考全国Ⅲ卷理数】a ，b 为空间中两条互相垂直的直线，等腰直角三角形ABC 的直角边AC 所在直线与a ，b 都垂直，斜边AB 以直线AC 为旋转轴旋转，有下列结论：①当直线AB 与a 成60°角时，AB 与b 成30°角；②当直线AB 与a 成60°角时，AB 与b 成60°角；③直线AB 与a 所成角的最小值为45°；④直线AB 与a 所成角的最大值为60°. 其中正确的是________.（填写所有正确结论的编号）【解析】设1AC BC ==.由题意，AB 是以AC 为轴,BC 为底面半径的圆锥的母线，由,AC a AC b ⊥⊥，又AC ⊥圆锥底面，所以在底面内可以过点B ，作BD a ∥，交底面圆C 于点D ，如图所示，连接DE ，则DE ⊥BD ，DE b ∴∥，连接AD ，等腰ABD △中，AB AD ==当直线AB 与a 成60°角时，60ABD ∠=o ，故BD =Rt BDE △中，2,BE DE =∴=B 作BF ∥DE ，交圆C 于点F ，连接AF ，由圆的对称性可知BF DE ==ABF ∴△为等边三角形，60ABF ∴∠=o ，即AB 与b 成60°角，②正确，①错误.由图可知③正确；很明显，可以满足平面ABC ⊥直线a ，则直线AB 与a 所成角的最大值为90°，④错误.故正确的是②③.【答案】②③8.【2016高考浙江文数】如图，已知平面四边形ABCD ，AB =BC =3，CD =1，ADADC =90°．沿直线AC 将△ACD 翻折成△ACD '，直线AC 与BD '所成角的余弦的最大值是______．【解析】设直线AC 与'BD 所成角为θ．设O 是AC 中点，由已知得AC =如图，以OB 为x 轴，OA 为y 轴，过O 与平面ABC 垂直的直线为z轴，建立空间直角坐标系，由(0,2A，(2B，(0,2C -，作DH AC ⊥于H ，翻折过程中，'D H 始终与AC 垂直，26CD CH CA ===，则3OH =，DH =='(,sin )636D αα-，则'sin )6236BD αα=--uuu r ，与CA uu r 平行的单位向量为(0,1,0)n =r ， 所以cos cos ',BD n θ=<>uuu r r ''BD n BD n⋅=uuu r r uuu r rcos 1α=时，cos θ取最大值9．9.【2017天津，文17】如图，在四棱锥P ABCD -中，AD ⊥平面PDC ，AD BC ∥，PD PB ⊥，1AD =，3BC =，4CD =，2PD =.（I ）求异面直线AP 与BC 所成角的余弦值；（II ）求证：PD ⊥平面PBC ；（Ⅲ）求直线AB 与平面PBC 所成角的正弦值.【分析】（Ⅰ）异面直线所成的角一般都转化为相交线所成的角，//AD BC ，所以PAD ∠即为所求，根据余弦定理求得，但本题可证明AD PD ⊥，所以cosAD PAD AP ∠=；（Ⅱ）要证明线面垂直，根据判断定理，证明线与平面内的两条相交直线垂直，则线与面垂直，即证明,PD BC PD PB ⊥⊥；（Ⅲ）根据（Ⅱ）的结论，做//DF AB ，连结PF ,DFP ∠即为所求【解析】（Ⅰ）解：如图，由已知AD //BC ，故DAP ∠或其补角即为异面直线AP 与BC 所成的角.因为AD ⊥平面PDC ，所以AD ⊥PD .在Rt △PDA 中，由已知，得225AP AD PD =+=，故5cos AD DAP AP ∠==. 所以，异面直线AP 与BC C（Ⅱ）证明：因为AD ⊥平面PDC ，直线PD ⊂平面PDC ，所以AD ⊥PD .又因为BC //AD ，所以PD ⊥BC ，又PD ⊥PB ，所以PD ⊥平面PB C.10.【2019年高考浙江卷】如图，已知三棱柱111ABC A B C -，平面11A ACC ⊥平面ABC ,90ABC ∠=︒，1130,,,BAC A A AC AC E F ∠=︒==分别是AC ，A 1B 1的中点. （1）证明：EF BC ⊥；（2）求直线EF 与平面A 1BC 所成角的余弦值.【解析】方法一：（1）连接A 1E ，因为A 1A =A 1C ，E 是AC 的中点，所以A 1E ⊥AC ．又平面A 1ACC 1⊥平面ABC ，A 1E ⊂平面A 1ACC 1， 平面A 1ACC 1∩平面ABC =AC ，所以，A 1E ⊥平面ABC ，则A 1E ⊥BC ．又因为A 1F ∥AB ，∠ABC =90°，故BC ⊥A 1F ．所以BC ⊥平面A 1EF ．因此EF ⊥BC ．（2）取BC 中点G ，连接EG ，GF ，则EGFA 1是平行四边形．由于A 1E ⊥平面ABC ，故A 1E ⊥EG ，所以平行四边形EGFA 1为矩形．由（1）得BC ⊥平面EGFA 1，则平面A 1BC ⊥平面EGFA 1，所以EF 在平面A 1BC 上的射影在直线A 1G 上．连接A 1G 交EF 于O ，则∠EOG 是直线EF 与平面A 1BC 所成的角（或其补角）．不妨设AC =4，则在Rt △A 1EG 中，A 1E ，EG O 为A 1G 的中点，故12A G EO OG ===， 所以2223cos 25EO OG EG EOG EO OG +-∠==⋅．因此，直线EF 与平面A 1BC 所成角的余弦值是35． 方法二：（1）连接A 1E ，因为A 1A =A 1C ，E 是AC 的中点，所以A 1E ⊥AC .又平面A 1ACC 1⊥平面ABC ，A 1E ⊂平面A 1ACC 1，平面A 1ACC 1∩平面ABC =AC ，所以，A 1E ⊥平面ABC ．如图，以点E 为原点，分别以射线EC ，EA 1为y ，z 轴的正半轴，建立空间直角坐标系E –xyz ．不妨设AC =4，则A 1（0，0，B 1，0），1B ，3,2F ，C (0，2，0)．因此，3,2EF =u u u r ，(BC =u u u r ．由0EF BC ⋅=u u u r u u u r 得EF BC ⊥． （2）设直线EF 与平面A 1BC 所成角为θ．由（1）可得1=(310)=(0223)BC A C --u u u r u u u u r ，，，，，．设平面A 1BC 的法向量为n ()x y z =，，，由100BC A C ⎧⋅=⎪⎨⋅=⎪⎩u u u r n n，得00y y ⎧+=⎪⎨=⎪⎩， 取n (11)=，故||4sin |cos |=5|||EF EF EF θ⋅==⋅u u u r u u u r u u u r ，n n n |， 因此，直线EF 与平面A 1BC 所成的角的余弦值为35．2.【2017课标1，文6】如图，在下列四个正方体中，A ，B 为正方体的两个顶点，M ，N ，Q 为所在棱的中点，则在这四个正方体中，直接AB 与平面MNQ 不平行的是（ ） A ． B ．C ．D ．【解析】本题考点是线面平行的判断问题，由题意可知：第二个选项中AB ∥MQ ，在直线AB ∥平面MNQ ，第三个选项同样可得AB ∥MQ ，直线AB ∥平面MNQ ，第四个选项有AB ∥NQ ，直线AB ∥平面MNQ ，只有选项A 不符合要求【答案】A2．空间中，可以确定一个平面的条件是（ ）A ．两条直线B ．一点和一条直线C ．一个三角形D ．三个点【解析】不共线的三点确定一个平面，C 正确；A 选项，只有这两条直线相交或平行才能确定一个平面；B 选项，一条直线和直线外一点才能确定一个平面；D 选项，不共线的三点确定一个平面.【答案】C3.在三棱锥A －BCD 的棱AB 、BC 、CD 、DA 上分别取E 、F 、G 、H 四点，如果EF ∩HG ＝P ，则点P （ ）A .一定在直线BD 上B .一定在直线AC 上 【模拟考场】C .在直线AC 或BD 上 D .不在直线AC 上，也不在直线BD 上【解析】如图所示，∵EF ⊂平面ABC ，HG ⊂平面ACD ，EF ∩HG ＝P ，∴P ∈平面ABC ，P ∈平面ACD .又∵平面ABC ∩平面ACD ＝AC ，∴P ∈AC ，故选B .【答案】B4.已知平面α和直线l ，则在平面α内至少有一条直线与直线l ( )A.平行B.垂直C.相交D.以上都有可能【解析】本题的考点是直线与平面的位置关系，直线与直线的位置关系，若直线l 与平面α相交，则在平面α内不存在直线与直线l 平行，故A 错误；若直线l ∥平面α，则在平面α内不存在直线与l 相交，故C 错误；对于直线l 与平面α相交，直线l 与平面α平行，直线l 在平面α内三种位置关系，在平面α内至少有一条直线与直线l 垂直，故选B.【答案】B5.如图，四棱锥P ABCD -中，90ABC BAD ∠=∠=︒，2BC AD =，PAB ∆和PAD ∆都是等边三角形，则异面直线CD 和PB 所成角的大小为（ ）A ．90︒B ．75︒C ．60︒D ．45︒【解析】设1AD =，则2BC =，过A 作//AE CD 交BC 于E ，则AD CE =，过E 作//EF PB 交PC于F ，则AEF ∠即为为所求，如图所示，过F 作//FG CD 交PD 于G ，连接AG ，则四边形AEFG 是梯形，其中//FG AE ，12EF =G 作//GH EF 交AE 于H ，则GHA AEF ∠=∠，在GHA ∆中，1,,222GH EF AH AE FG AG ===-===则 222AG GH AH =+，所以90AEF ∠=︒，故选A.【答案】A6.不在同一条直线上的三点A 、B 、C 到平面α的距离相等，且A ∉α，给出以下三个命题：①△ABC 中至少 有一条边平行于α；②△ABC 中至多有两边平行于α；③△ABC 中只可能有一条边与α相交.其中真命题是_____________.【解析】直线与平面的位置关系，平面与平面的位置关系，如图，三点A 、B 、C 可能在α的同侧，也可能在α两侧，其中真命题是①.【答案】①7.已知A 是△BCD 所在平面外的一点，E ，F 分别是BC ，AD 的中点，(1)求证：直线EF 与BD 是异面直线；(2)若AC ⊥BD ，AC ＝BD ，求EF 与BD 所成的角．【解析】本题考点反证法证明异面直线，异面直线所成的角.(1)证明：假设EF 与BD 不是异面直线，则EF 与BD 共面，从而DF 与BE 共面，即AD 与BC 共面，所以A 、B 、C 、D 在同一平面内，这与A 是△BCD 所在平面外的一点相矛盾．故直线EF 与BD 是异面直线．(2)取CD 的中点G ，连接EG 、FG ，则EG ∥BD ，所以直线EF 与EG 所成的角即为异面直线EF 与BD 所成的角．在Rt △EGF 中，由EG ＝FG ＝12AC ，可得∠FEG ＝45°，即异面直线EF 与BD 所成的角为45°.8.如图，已知正方体ABCD －A 1B 1C 1D 1的棱长为3，M ，N 分别是棱AA 1，AB 上的点，且AM ＝AN ＝1.（1）证明：M ，N ，C ，D 1四点共面；（2）平面MNCD 1将此正方体分为两部分，求这两部分的体积之比.【解析】本题考点是多点共面的证明，平面分几何体的体积之比.（1）证明：连接A 1B ，在四边形A 1BCD 1中，A 1D 1∥BC 且A 1D 1＝BC ，所以四边形A 1BCD 1是平行四边形.所以A 1B ∥D 1C. 在△ABA 1中，AM ＝AN ＝1，AA 1＝AB ＝3，所以1AM AN AA AB， 所以MN ∥A 1B ，所以MN ∥D 1C.所以M ，N ，C ，D 1四点共面.（2）记平面MNCD 1将正方体分成两部分的下部分体积为V 1，上部分体积为V 2，连接D 1A ，D 1N ，DN ，则几何体D 1－AMN ，D 1－ADN ，D 1－CDN 均为三棱锥，所以V 1＝111D AMN D ADN D CDN V V V ---++＝13S △AMN ·D 1A 1＋13S △ADN ·D 1D ＋13S △CDN ·D 1D ＝13×12×3＋13×32×3＋13×92×3＝132. 从而V 2＝1111ABCD A B C D V -－V 1＝27－132＝412，所以121341V V =， 所以平面MNCD 1分此正方体的两部分体积的比为1341.。

考点35立体几何中的向量方法一、解答题1.（2011·福建卷理科·Ｔ20）(本小题满分14分)如图，四棱锥P-ABCD中，PA⊥底面ABCD.四边形ABCD中，AB⊥AD，AB+AD=4，CD=2，︒∠45CDA.=（I）求证：平面PAB⊥平面PAD；（II）设AB=AP.（i）若直线PB与平面PCD所成的角为︒30，求线段AB的长；（ii）在线段AD上是否存在一个点G，使得点G到点P，B，C，D的距离都相等？说明理由.【思路点拨】(1)证面面PAB中的直线AB PAD⊥面，也可⊥面，从而可推得面PAB PAD以建立坐标系证明两面的法向量垂直；（2）以A为坐标原点，建立空间直角坐标系-A xyz，然后用空间向量法进行求解探究.【精讲精析】（I）因为PA⊥平面ABCD，AB⊂平面ABCD，所以PA AB解法1：⊥，又,A B A D P A A D A⊥=，所以AB⊥平面PAD.又AB⊂平面PAB，所以平面PAB⊥平面PAD.(2)以A为坐标原点，建立空间直角坐标系A xyz-（如图）.在平面ABCD内，作//⊥.CE AB交AD于点E，则CE AD在Rt CDE ∆中，cos451DE CD =⋅︒=.设AB AP t ==，则(,0,0),(0,0,)B t P t . 由AB+AD ＝4得AD ＝4t -，所以(0,3,0),1,3,0),(0,4,0)E t C t D t ---（，(1,1,0),(0,4,).CD PD t t =-=--（i ）设平面PCD 的法向量为=(,,),x y z n 由,,CD PD ⊥⊥n n 得0(4)0.x y t y tz -+=⎧⎨--=⎩取x t =，得平面PCD 的一个法向量(,,4)t t t =-n .cos60||,|||PBPB ⋅︒=⋅n n |即21,2= 解得45t =或4t =（舍去，因为40AD t =->），所以AB ＝4.5（ii ）假设在线段AD 上存在一个点G （如下图），使得点G 到点P 、B 、C 、D 的距离都相等，设G （0,m,0）(其中04m t ≤≤-)，则(1,3,0),(0,4,0),(0,,)GC t m GD t m GP m t =--=--=-由||||GC GD =得2221(3)(4),t m t m +--=--即3t m =-.① 由||||GD GP =得222(4).m t m t --=+②C由①②消去t ，化简得23+40.m m -=③由于方程③没有实数根，所以在线段AD 上不存在一个点G ，使得点G 到点P ，C ，D 的距离都相等. 解法2：（I ）同解法1. （Ⅱ）（i ）同解法1 .（ii ）假设在线段AD 上存在一个点G ，使得点G 到点P ，B ，C ，D 的距离都相等. 由GC ＝GD ，得45,GCD GDC ∠=∠=︒从而90,CGD ∠=︒即CG AD ⊥，所以cos451GD CD =⋅︒=.设AB λ=，则4AD λ=-，AG ＝AD-GD＝3λ-.在Rt ABG ∆中，1,GB ==>这与GB ＝GD 矛盾.所以在线段AD 上不存在一个点G ，使得点G 到点P 、B 、C 、D 的距离都相等. 2. （2011·江苏高考·Ｔ22）（本小题满分10分）如图，在正四棱柱1111ABCD A B C D -中，12,1AA AB ==，点N 是BC 的中点，点M 在1CC 上，设二面角1A DN M --的大小为θ。

高考数学考点重点剖析立体几何与空间向量的综合应用高中数学是高考的一大重点科目，其中立体几何与空间向量是考试中常见的考点之一。

本文将重点剖析这两个知识点在高考中的综合应用。

一、立体几何的基本概念和性质立体几何是研究三维空间中点、线、面、体及其性质的数学分支。

在高考中，考察立体几何的题目常常需要灵活运用基本概念和性质来解决问题。

1. 三视图三视图是描述立体物体的三个视图，分别是主视图、俯视图和左视图。

通过观察三视图，可以推理出立体物体的形状、大小等信息。

2. 图形的空间定位在解决立体几何题目时，常常需要判断点、线、面的位置关系。

例如，可以通过判断两直线的垂直、平行关系，或者利用截距定理、距离公式等来确定点在空间中的位置。

3. 空间几何体的计算在高考中，计算空间几何体的体积、表面积等也是重要的考点。

对于常见的立体几何体如正方体、长方体、圆柱、锥体等，需要掌握相应的计算公式，并能够根据实际情况进行灵活运用。

二、空间向量的基本概念和性质空间向量是研究三维空间中向量的数量和运算规律的数学分支。

在高考中，考察空间向量的题目常常需要理解向量的基本概念和性质，并能够熟练运用到解决实际问题中。

1. 三维向量的坐标表示三维向量通常用顶点表示法表示，即向量的坐标表示为(x, y, z)。

掌握向量坐标的表示方法对于解题非常重要。

2. 向量的数量积与向量积数量积和向量积是空间向量运算的两个重要概念。

数量积可以用来计算两个向量之间的夹角，同时也具有判断垂直、平行关系的性质；向量积可以用来计算两个向量所围成的平行四边形的面积，并且具有右手法则、分配律等性质。

3. 平面与直线的方程在解决空间向量的题目时，常常需要通过建立方程组来确定平面或直线的方程。

例如，可以利用向量方程、点法式、面法式等来描述平面的方程，运用点向式、轨迹式等来描述直线的方程。

三、综合应用示例分析在高考数学中，立体几何与空间向量的综合应用题目较为常见。

这类题目通常需要通过空间向量的方法解决立体几何的问题，或者利用立体几何的概念解决空间向量的问题。

2011年普通高等学校招生全国统一考试（湖南卷）数学（理工农医类）一选择题：本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项符合题目要求的.1.若,a b ∈R ，i 为虚数单位，且(i)i i a b +=+，则 （ ） A ．1,1a b == B ．1,1a b =-= C ．1,1a b =-=- D ．1,1a b ==-【测量目标】复数的四则运算.【考查方式】利用复数相等的条件直接求值. 【难易程度】容易 【参考答案】D【试题解析】因(i)i 1i i a a b +=-+=+，根据复数相等的条件可知1,1a b ==-. 2.设{1,2}M =，2{}N a =，则“1a =”是“N M ⊆”则 （ ） A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分又不必要条件 【测量目标】集合间的关系,充分必要条件. 【考查方式】给出两个集合直接考查. 【难易程度】容易 【参考答案】A【试题解析】因“1a =”，即{1}N =，满足“N M ⊆”，反之“N M ⊆”，则2{}={1}N a =，或2{}={2}N a =，不一定有“1a =”.3.如图一是某几何体的三视图，则该几何体的体积为 （ ）第3题图A ．9π122+ B ．9π182+ C ．9π42+ D ．36π18+【测量目标】由三视图求几何体的体积.【考查方式】给出三视图，通过判断直接求体积. 【难易程度】容易 【参考答案】B【试题解析】由三视图可知该几何体是一个长方体和球构成的组合体， 其体积3439π()332π+18322V =+⨯⨯=. 4.通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的列联表：男 女 总计爱好40 20 60 不爱好20 30 50 总计60 50 110由22()()()()()n ad bc K a b c d a c b d -=++++算得22110(40302020)7.860506050K ⨯⨯-⨯=≈⨯⨯⨯ 附表：2()P K k … 0.0500.010 0.001 k3.8416.63510.828参照附表，得到的正确结论是 （ ）A ．在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关”B ．在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别无关”C ．有99%以上的把握认为“爱好该项运动与性别有关”D ．有99%以上的把握认为“爱好该项运动与性别有关” 【测量目标】独立性检验.【考查方式】给出统计图表直接考查. 【难易程度】容易 【参考答案】C【试题解析】由27.8 6.635,K ≈>而2( 6.635)0.010P K =…，故由独立性检验的意义可知选C.5.设双曲线2221(0)9x y a a -=>的渐近线方程为320x y ±=，则a 的值为 （ ）A ．4B ．3C ．2D ．1【测量目标】双曲线的简单几何性质.【考查方式】由双曲线方程直接求出渐近线方程，再结合给出的渐近线方程比较求解. 【难易程度】容易 【参考答案】C【试题解析】：由双曲线方程可知渐近线方程为3y x a=±，故可知2a =. 6. 由直线ππ,,033x x y =-==与曲线cos y x =所围成的封闭图形的面积为（ ） A ．12 B ．1 C．2D【测量目标】定积分的几何意义.【考查方式】直接给出曲线和直线方程求面积. 【难易程度】容易 【参考答案】D【试题解析】由定积分知识可得ππ33ππ33cosd sin |(22S x x --===-=⎰7. 设1m >，在约束条件1y xy mx x y ⎧⎪⎨⎪+⎩………下，目标函数z x my =+的最大值小于2，则m 的取值范围为 （ ） A．(1,1 B．(1)+∞ C ．(1,3) D ．(3,)+∞ 【测量目标】线性规划求最值.【考查方式】给出约束条件和目标函数的范围求目标函数y 轴系数的值. 【难易程度】容易 【参考答案】A【试题解析】可知z x my =+在点1(,)11m m m++取最大值，由 21211m m m+<++解得11m <<. 8.设直线x t =与函数2(),()ln f x x g x x ==的图像分别交于点,M N ，则当||MN 达到最小时t 的值为 （ ）A ．1B ．12C ．2D ．2【测量目标】利用导数判断单调性求最值.【考查方式】利用直线与曲线相交，求相交直线方程再运用导数性质求解. 【难易程度】容易 【参考答案】D【试题解析】由题2||ln MN x x =-，(0)x >不妨令2()ln h x x x =-，则1()2h x x x'=-，令()0h x '=解得2x =，因(0,)2x ∈时，()0h x '<，当()2x ∈+∞时，()0h x '>，所以当2x =时，||MN 达到最小，即2t =.二、填空题：本大题共8小题，考生作答7小题，每小题5分，共35分，把答案填在答题卡中对应题号的横线上.一、选做题（请考生在第9、10、11三题中任选两题作答，如果全做，则按前两题记分） 9.在直角坐标系xOy 中，曲线C 1的参数方程为cos ,1sin x y αα=⎧⎨=+⎩（α为参数）在极坐标系（与直角坐标系xOy 取相同的长度单位，且以原点O 为极点，以x 轴正半轴为极轴）中，曲线2C 的方程为()cos sin 10ρθθ-+=，则1C 与2C 的交点个数为 . 【测量目标】坐标系与参数方程.【考查方式】给出极坐标方程与参数方程，将其转化为普通方程后解不等式求解. 【难易程度】容易【参考答案】2【试题解析】曲线221:(1)1C x y +-=，2:10C x y -+=，由圆心到直线的距离01d ==<，故1C 与2C 的交点个数为2. 10.设,x y ∈R ,则222211()(4)x y y x++的最小值为 . 【测量目标】不等式选讲.【考查方式】给出两个乘式直接考查. 【难易程度】中等 【参考答案】9【试题解析】由柯西不等式可知2222211()(4)(12)9x y y x+++=…. 11.如图，,A E 是半圆周上的两个三等分点，直径4BC =，AD BC ⊥,垂足为D , BE 与AD 相交与点F ，则AF 的长为 .第11题图【测量目标】几何证明选讲.【考查方式】通过线段和圆的位置关系考查. 【难易程度】容易【参考答案】3【试题解析】由题可知，60AOB EOC ∠=∠=，2OA OB ==,得1OD BD ==,3DF =，又23AD BD CD ==，所以3AF AD DF =-=. 二、必做题（12~16题）12．设n S 是等差数列*{}()n a n ∈N 的前n 项和，且141,7a a ==，则5______S = 【测量目标】等差数列的前n 项和.【考查方式】给出等差数列某两项的值求出通项再求和. 【难易程度】容易 【参考答案】25【试题解析】由141,7a a ==可得11,2,21n a d a n ===-，所以5(19)5252S +⨯==. 13．若执行如图所示的框图，输入1231,2,3,2x x x x ====， 则输出的数等于 .第13 题图【测量目标】循环结构的程序框图. 【考查方式】直接给出程序框图考查. 【难易程度】中等 【参考答案】23【试题解析】由框图的算法功能可知，输出的数为三个数的方差，则222(12)(22)(32)233S -+-+-==. 14．在边长为1的正三角形ABC 中，设2,3BC BD CA CE == ，则________AD BE =.【测量目标】平面向量在平面几何中的运用. 【考查方式】给出向量间的关系求解. 【难易程度】容易 【参考答案】14-【试题解析】由题12AD CD CA CB CA =-=- ，13BE CE CB CA CB =-=-，所以111171()()232364AD BE CB CA CA CB CB CA =--=--+=-. 15．如图， EFGH 是以O 为圆心，半径为1的圆的内接正方形，将一颗豆子随机地扔到该圆内，用A 表示事件“豆子落在正方形EFGH 内”，B 表示事件“豆子落在扇形OHE （阴影部分）内”，则（1）=______P A （）；（2）=______P B A （|）第15题图【测量目标】几何概型.【考查方式】利用两个图形面积的比值求解. 【难易程度】容易 【参考答案】（1）2π；（2）1=4PB A （|） 【试题解析】（1）由几何概型概率计算公式可得2==πS P A S 正圆（）； （2）由条件概率的计算公式可得21×1π4===24πP AB P B A P A （）（|）（）.16.对于*n ∈N ，将n 表示为1210012122222k k k k k n a a a a a ---=⨯+⨯+⨯++⨯+⨯ ，当0i =时，1i a =，当1i k 剟时，i a 为0或1.记()I n 为上述表示中i a 为0的个数，（例如0112=⨯，2104120202=⨯+⨯+⨯：故(1)0,(4)2I I ==）则（1）(12)_____I = （2）127()12______I n n ==∑【测量目标】排列组合及其应用. 【考查方式】利用特定的条件求解. 【难易程度】较难 【参考答案】（1）2；（2）1093【试题解析】（1）因3211212+120202=⨯⨯+⨯+⨯，故(12)2I =；（2）在2进制的(2)k k …位数中，没有0的有1个，有1个0的有11C k -个，有2个0的有21C k -个，……有m 个0的有1C m k -个，……有1k -个0的有11C 1k k --=个.故对所有2进制为k 位数的数n ，在所求式中的()2I n 的和为：0112211111112C 2C 2C 23k k k k k k ------⨯++++=. 又712721=-恰为2进制的最大7位数，所以1277()1122231093I n k n k -===+=∑∑.三．解答题：本大题共6小题，共75分，解答应写出文字说明、证明过程或演算步骤. 17.（本小题满分12分）在ABC △中，角,,A B C 所对的边分别为,,a b c ，且满足sin cos c A a C =.（I ）求角C 的大小；（II πcos()4A B -+的最大值，并求取得最大值时角,A B 的大小． 【测量目标】正弦定理，三角函数的最值. 【考查方式】给出边角之间的关系求解. 【难易程度】容易 【试题解析】（I ）由正弦定理得sin sin sin cos .C A A C = 因为0π,A <<所以sin 0.A >πsin cos .cos 0,tan 1,4C C C C C =≠==从而又所以则.(步骤1) （II ）由（I ）知3π.4B A =-于是 πcos()cos(π)4A B A A -+=--πcos 2sin().6A A A =+=+3πππ11ππππ0,<+<,=,,46612623A A A A <<∴+= 从而当即时π2sin()6A +取最大值2．（步骤2）πcos()4A B -+的最大值为2，此时π5π,.312A B ==（步骤3） 18. 某商店试销某种商品20天，获得如下数据：当天营业结束后检查存货，若发现存货少于2件，则当天进货补充．．至3件，否则不进货．．．，将频率视为概率.(Ⅰ）求当天商品不进货．．．的概率； （Ⅱ）记X 为第二天开始营业时该商品的件数，求X 的分布列和数学期望. 【测量目标】对立事件的概率，离散型随机变量的期望. 【考查方式】运用实际生活背景考查.【难易程度】容易 【试题解析】（I ）P （“当天商店不进货”）=P （“当天商品销售量为0件”）+P （“当天商品销售量1件”）=153202010+=.（步骤1） （II ）由题意知，X 的可能取值为2，3.51(2)()204P X P ====“当天商品销售量为1件”； (3)()+()+(1953)++32020204P X P P P ====“当天商品销售量为0件”“当天商品销售量为2件”“当天商品销售量为3件”（步骤）故X 的分布列为X2 3 P 14 34 X 的数学期望为13112+3=444EX =⨯⨯.（步骤4）19.（本题满分12分）如图，在圆锥PO 中，已知PO O = 的直径2,,A B C A B D A C=是的中点,为的中点． （I ）证明：;POD PAC ⊥平面平面 （II ）求二面角B PA C --的余弦值．第18题图【测量目标】面面垂直，二面角.【考查方式】在圆锥中考查. 【难易程度】容易 【试题解析】（I ）连接OC ， 因为OA OC =,D 为AC 中点，所以AC OD ⊥. 又,,.PO O AC O AC PO ⊥⊂⊥ 底面底面所以因为,OD PO 是平面POD 内的两条相交直线，所以AC POD ⊥平面而AC PAC ⊂平面，所以POD PAC ⊥平面平面.（步骤1）（II ）在平面POD 中，过O 作OH PD ⊥于H ，由（I ）知，POD PAC ⊥平面平面,所以,OH PAC ⊥平面又,PA PAC ⊂平面所以PA OH ⊥.在平面PAO 中，过O 作OG PA G ⊥于,连接HG ,则有PA OGH ⊥平面， 从而PA HG ⊥，所以OGH ∠是二面角B PA C --的平面角．（步骤2）在Rt ,sin 452ODA OD OA ==△中在Rt ,POD OH ===△中在Rt ,POA OG ===△中在Rt ,sin OH OHG OGH OG ∠===△中所以cos 5OGH ∠=. 故二面角B PA C --的余弦值为5.（步骤3）第19题图20. 如图，长方形物体E 在雨中沿面P （面积为S ）的垂直方向作匀速移动，速度为(0)v v >，雨速沿E 移动方向的分速度为()c c ∈R .E 移动时单位时间．．．．内的淋雨量包括两部分：（1）P 或P 的平行面（只有一个面淋雨）的淋雨量，假设其值与v c -×S 成正比，比例系数为110；（2）其它面的淋雨量之和，其值为12，记y 为E 移动过程中的总淋雨量，当移动距离d =100，面积S =32时. （Ⅰ）写出y 的表达式；（Ⅱ）设0＜v …10,0＜c …5，试根据c 的不同取值范围，确定移动速度v ，使总淋雨量y 最少.第19题图【测量目标】分段函数模型，利用函数单调性及最值. 【考查方式】利用将立体几何与函数综合考查. 【难易程度】中等【试题解析】（I ）由题意知，E 移动时单位时间内的淋雨量为31||202v c -+， 故100315(||)(3||10)202y v c v c v v=-+=-+.（步骤1） （II ）由(I)知，当0v c <…时，55(310)(3310)15c y c v v v+=-+=-； 当10c v <…时，55(103)(3310)15c y v c v v-=-+=+. 故5(310)15,05(103)15,10c v c vy c c v v +⎧-<⎪⎪=⎨-⎪+<⎪⎩…….（步骤2）(1)当1003c <…时，y 是关于v 的减函数.故当10v =时，min 3202cy =-.（步骤3） (2) 当1053c <…时，在(0,]c 上，y 是关于v 的减函数；在(,10]c 上，y 是关于v 的增函数；故当v c =时，min 50y c=.（步骤4） 21.(本小题满分13分） 如图，椭圆221221(0)x y C a b a b +=>>：，x轴被曲线22:C y x b =- 截得的线段长等于1C 的长半轴长.（Ⅰ）求1C ，2C 的方程；（Ⅱ）设2C 与y 轴的交点为M ，过坐标原点O 的直线l 与2C 相交于点A,B ,直线MA ,MB 分别与1C 相交于D ,E .（i ）证明：MD ME ⊥；(ii)记△MAB ,△MDE 的面积分别是12,S S .问：是否存在直线l ,使得121732S S =? 请说明理由.第21题图【测量目标】椭圆的标准方程，直线与椭圆的位置关系. 【考查方式】利用直线与椭圆相交的位置关系和条件考查. 【难易程度】较难【试题解析】（I）由题意知c e a ==2a b =，又a =，解得2,1a b ==.故1C ，2C 的方程分别为2221,14x y y x +==-. （步骤1） （II ）（i ）由题意知，直线l 的斜率存在，设为k ， 则直线l 的方程为y kx =.由21y kx y x =⎧⎨=-⎩得210x kx --=，（步骤2） 设1122(,),(,)A x y B x y ，则12,x x 是上述方程的两个实根，于是1212,1x x k x x +==-. 又点M 的坐标为(0,1)-，所以2221212121212121211(1)(1)()1111MA MBy y kx kx k x x k x x k k k k x x x x x x +++++++-++=====--故MA MB ⊥，即MD ME ⊥.（步骤3）（ii ）设直线MA 的斜率为1k ，则直线MA 的方程为11y k x =-，由1211y kx y x =-⎧⎨=-⎩解得01x y =⎧⎨=-⎩或1211x k y k =⎧⎨=-⎩，则点A 的坐标为211(,1)k k -（步骤4） 又直线MB 的斜率为11k -，同理可得点B 的坐标为21111(,1)k k --.于是211111111||||||||.22||k S MA MB k k k +==-= （步骤5）由1221440y k x x y =-⎧⎨+-=⎩得2211(14)80k x k x +-=，解得01x y =⎧⎨=-⎩或12121218144114k x k k y k ⎧=⎪+⎪⎨-⎪=⎪+⎩，则点D 的坐标为2112211841(,)1414k k k k -++；（步骤6） 又直线ME 的斜率为11k -，同理可得点E 的坐标211221184(,)44k k k k --++ 于是2112221132(1)||1||||2(14)(4)k k S MD ME k k +==++ 因此21122111(417)64S k S k =++（步骤7） 由题意知，21211117(417)6432k k ++=,解得214k = 或2114k =. 又由点,A B 的坐标可知，21211111111k k k k k k k -==-+，所以3.2k =± 故满足条件的直线l 存在，且有两条，其方程分别为32y x =和32y x =-.（步骤8） 22.（本小题满分13分）已知函数f (x ) =3x ，g (x )=x（Ⅰ）求函数h (x )=f (x )-g (x )的零点个数，并说明理由；（Ⅱ）设数列*{}()n a n ∈N 满足1(0)a a a =>，1()()n n f a g a +=，证明：存在常数M ,使得对于任意的*n ∈N ，都有n a …M . 【测量目标】利用导数求单调性，不等式恒成立问题.【考查方式】给出两个函数式，利用导数及不等式求解.【难易程度】较难【试题解析】（I）由3()h x x x =-知，[0,)x ∈+∞，而(0)0h =，且(1)10,(2)60h h =-<=，则0x =为()h x 的一个零点，且()h x 在12（，）内有零点，因此()h x 至少有两个零点（步骤1） 122()(1)h x x x x -=--，记122()1x x x ϕ-=--，则321()22x x x ϕ-'=+. 当(0,)x ∈+∞时，()0x ϕ'>，因此()x ϕ在(0,)+∞上单调递增，则()x ϕ在(0,)+∞内至多只有一个零点.因此()h x 在(0,)+∞内也至多只有一个零点，综上所述，()h x 有且只有两个零点.（步骤2） （II ）记()h x 的正零点为0x，即300x x =（1）当0a x <时，由1a a =，即10a x <.而332100a a x x ==，因此20a x <，由此猜测：0n a x <.下面用数学归纳法证明： ①当1n =时，10a x <显然成立；（步骤3） ②假设当(1)n k k =…时，有0k a x <成立，则当1n k =+时，由13300k k a a x x +=+<知，10k a x +<，因此，当1n k =+时，10k a x +<成立. 故对任意的*n ∈N ，0n a x <成立.（步骤4）（2）当0a x …时，由（1）知，()h x 在0(,)x +∞上单调递增.则0()()0h a h x =…，即3a a +….从而2331a a a a ==，即2a a …，由此猜测：n a a ….下面用数学归纳法证明：①当1n =时，1a a …显然成立；（步骤5） ②假设当(1)n k k =…时，有k a a …成立，则当1n k =+时，由133k k a a a a +=+知，1k a a +…，因此，当1n k =+时，1k a a +…成立.故对任意的*n ∈N ，n a a …成立. 综上所述，存在常数0max{,}M x a =，使得对于任意的*n ∈N ，都有n a M ….（步骤6）。