2007年高考理科数学“立体几何”题

C B AG H MDE F1B 1A 1D1CN2007-2011江苏高考数学 立体几何 考题评析2007年 立体几何 注：当年全卷共21道题 10道选择题 6道填空题 5道解答题分数5+5+12=22分4．已知两条直线,m n ，两个平面,αβ，给出下面四个命题：①//,m n m n αα⊥⇒⊥ ②//,,//m n m nαβαβ⊂⊂⇒ ③//,////m n m n αα⇒ ④//,//,m n m n αβαβ⊥⇒⊥ 其中正确命题的序号是（ ） A ．①、③； B ．②、④； C ．①、④； D ．②、③ 【解析】②中，m n ，有可能是异面直线；③中，n 有可能在α上，都不对，故选（C ）14．正三棱锥P ABC -的高为2，侧棱与底面ABC 所成角为45︒，则点A 到侧面PBC 的距离是.【解析】如图，∠PBO ＝45°，PO ＝OB ＝2，OD ＝1，BDPB ＝PDAD ＝3，1122AD PO PD AE ⋅=⋅， 得AE . 18．如图，已知1111ABCD A B C D -是棱长为3的正方体，点E 在1AA 上，点F 在1CC 上，且11AE FC ==，（1）求证：1,,,E B F D 四点共面；（4分）（2）若点G 在BC 上，23BG =，点M 在1BB 上， GM BF ⊥，垂足为H ，求证：EM ⊥面11BCC B ；（4分） （3）用θ表示截面1EBFD 和面11BCC B 所成锐二面角大小，求tan θ．（4分）【解析】本小题主要考查平面的基本性质、线线平行、线面垂直、二面角等基础知识和基本运算，考查空间想象能力、逻辑推理能力和运算能力． 解法一：（1）如图，在1DD 上取点N ，使1DN =，连结EN ，CN ， 则1AE DN ==，12CF ND ==．∵AE DN ∥，1ND CF ∥，∴四边形ADNE ，1CFD N 都为平行四边形． 从而EN AD ∥，1FD CN ∥．又∵AD BC ∥，∴EN BC ∥， ∴四边形BCNE 是平行四边形，由此推知CN BE ∥，从而1FD BE ∥．∴1E B F D ，，，四点共面．（2）如图，GM BF ⊥，又BM BC ⊥，∴BGM CFB =∠∠，tan tan BM BG BGM BG CFB =⋅=⋅∠∠23132BC BG CF =⋅=⨯=． ∵AE BM ∥，∴ABME 为平行四边形，从而AB EM ∥． 又∵AB ⊥平面11BCC B ，∴EM ⊥平面11BCC B ．1D1A A B C D 1C 1B ME F HG（3）如图，连结EH ．∵MH BF ⊥，EM BF ⊥，∴BF ⊥平面EMH ，得EH BF ⊥． ∴EHM ∠是所求的二面角的平面角，即EHM θ=∠． ∵MBH CFB =∠∠，∴sin sin MH BM MBH BM CFB =⋅=⋅∠∠1BM ===，∴tan EMMHθ== 解法二：（1）建立如图所示的坐标系，则(301)BE =，，，(032)BF =，，，1(333)BD =，，，∴1BD BE BF =+， ∴1BD ，BE ，BF 共面． 又∵它们有公共点B ，∴1E B F D ，，，四点共面．（2）如图，设(00)M z ，，，则2(0)3GM z =-，，， 而(032)BF =，，，由题设得23203GM BF z ⋅=-⨯+⨯=，解得1z =．∵(001)M ，，，(301)E ，，，有(300)ME =，，，又1(003)BB =，，，(030)BC =，，， ∴10ME BB =，0ME BC =，从而1ME BB ⊥，ME BC ⊥． ∴ME ⊥平面11BCC B ．（3）设向量(3)BP x y =，，⊥截面1EBFD ，于是BP BE ⊥，BP BF ⊥．而(301)BE =，，，(032)BF =，，，得330BP BE x =+=，360BP BF y =+=， 解得1x =-，2y =-，∴ (12 3)BP =--，，． 又(300)BA =，，⊥平面11BCC B ，∴BP 和BA 的夹角等于θ或πθ-（θ为锐角）．于是cos 14BP BA BP BAθ==． ∴tan θ=2008年 立体几何 注：从这一年开始 正卷共20道题 14道填空题 6道解答题附加题卷4选2，加2道解答题，共4道题 每题10分 共40分分数14+10＝24分A B C DE F16．如图，在四面体ABCD 中，CB CD AD BD =⊥，，点E F ，分别是AB BD ，的中点．求证：（1）直线//EF 面ACD ；（2）平面EFC ⊥面BCD ． 【解析】（1）∵E ，F 分别是AB BD ，的中点．∴EF 是△ABD 的中位线， ∴EF ∥AD ，∵EF ∥⊄平面ACD ，AD ⊂平面ACD ， ∴直线EF ∥平面ACD ；（2）∵AD ⊥BD ，EF ∥AD ， ∴EF ⊥BD ，∵CB =CD ，F 是BD 的中点， ∴CF ⊥BD ；又∵EF ∩CF =F ，∴BD ⊥平面EFC ，∵BD ⊂平面BCD ， ∴平面EFC ⊥平面B C D ．22．【必做题】如图，设动点P 在棱长为1的正方体1111-ABCD A BC D 的对角线1BD上， 记11D PD Bλ=；当APC ∠为钝角时，求λ的取值范围． 【解析】由题设可知，以DA 、DC 、1DD 为单位正交基底，建立如图所示的空间直角坐标系D xyz -，则有(1,0,0)A ，(1,1,0)B ，(0,1,0)C ，(0,0,1)D ； 由1(1,1,1)D B =-，得11(,,)D P D B λλλλ==-，∴11(,,)(1,0,1)(1,,1)PA PD D A λλλλλλ=+=--+-=---11(,,)(0,1,1)(,1,1)PC PD DC λλλλλλ=+=--+-=---； 显然APC ∠不是平角，∴APC ∠为钝角等价于：cos cos ,0PA PC APC PA PC PA PC∠=<>=<，则等价于0PA PC <；即：2(1)()()(1)(1)(1)(31)0λλλλλλλ--+--+-=--<，得113λ<<； ∴λ的取值范围是1(,1)3．2009年 立体几何分数5+5++14=24分8．在平面上，若两个正三角形的边长的比为1：2，则它们的面积比为1：4，类似地，在空间 内，若两个正四面体的棱长的比为1：2，则它们的体积比为 . 【解析】考查类比的方法．体积比为1：8．12．设α和β为不重合的两个平面，给出下列命题：（1）若α内的两条相交直线分别平行于β内的两条直线，则α平行于β；（2）若α外一条直线l 与α内的一条直线平行，则l 和α平行；（3）设α和β相交于直线l ，若α内有一条直线垂直于l ，则α和β垂直；（4）直线l 与α垂直的充分必要条件是l 与α内的两条直线垂直。

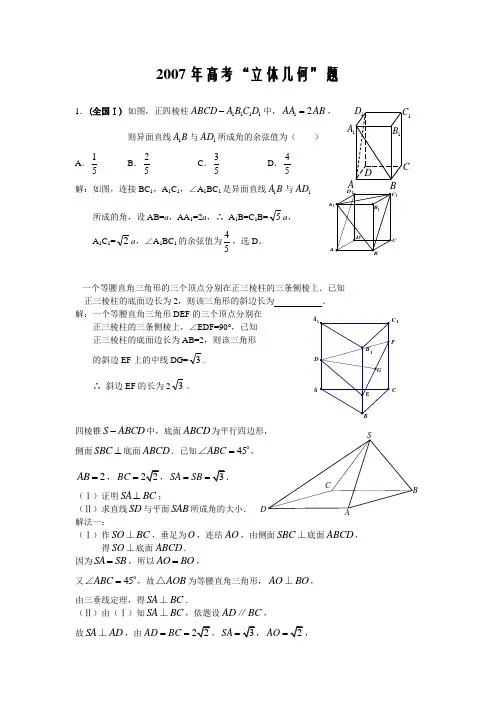
2007年高考“立体几何”题1．(全国Ⅰ) 如图，正四棱柱1111ABCD A B C D -中，12AA AB =，则异面直线1A B 与1AD 所成角的余弦值为（ ）A ．15B ．25C ．35D ．45解：如图，连接BC 1，A 1C 1，∠A 1BC 1是异面直线1A B 与1AD所成的角，设AB=a ，AA 1=2a ，∴ A 1B=C 1B=5a ， A 1C 1=2a ，∠A 1BC 1的余弦值为45，选D 。

一个等腰直角三角形的三个顶点分别在正三棱柱的三条侧棱上．已知 正三棱柱的底面边长为2，则该三角形的斜边长为 ． 解：一个等腰直角三角形DEF 的三个顶点分别在 正三棱柱的三条侧棱上，∠EDF=90°，已知 正三棱柱的底面边长为AB=2，则该三角形的斜边EF 上的中线DG=3. ∴ 斜边EF 的长为23。

四棱锥S ABCD -中，底面ABCD 为平行四边形， 侧面SBC ⊥底面ABCD ．已知45ABC =∠，2AB =，BC =SA SB ==（Ⅰ）证明SA BC ⊥；（Ⅱ）求直线SD 与平面SAB 所成角的大小． 解法一：（Ⅰ）作SO BC ⊥，垂足为O ，连结AO ，由侧面SBC ⊥底面ABCD ，得SO ⊥底面ABCD ． 因为SA SB =，所以AO BO =，又45ABC =∠，故AOB △为等腰直角三角形，AO BO ⊥， 由三垂线定理，得SA BC ⊥．（Ⅱ）由（Ⅰ）知SA BC ⊥，依题设AD BC ∥， 故SA AD ⊥，由AD BC ==SA =AO =1A AB1B1A1D1C CDC 1A CFAD BCA S得1SO =，SD =．SAB △的面积211122S ABSA ⎛=-= ⎝连结DB ，得DAB △的面积21sin13522S AB AD == 设D 到平面SAB 的距离为h ，由于D SAB S ABD V V --=， 得121133h S SO S =，解得h = 设SD 与平面SAB 所成角为α，则sin 11h SD α===． 所以，直线SD 与平面SBC 所成的我为arcsin11． 解法二：（Ⅰ）作SO BC ⊥，垂足为O ，连结AO ，由侧面SBC ⊥底面ABCD ，得SO ⊥平面ABCD ． 因为SA SB =，所以AO BO =．又45ABC =∠，AOB △为等腰直角三角形，AO OB ⊥． 如图，以O 为坐标原点，OA 为x 0)A ，，(0B ，(0C -，，(001)S ，，，(2，(0CB =，0SA CB =，所以SA BC ⊥．（Ⅱ）取AB 中点E ，022E ⎛⎫⎪ ⎪⎝⎭，，连结SE ，取SE 中点G ，连结OG ，12G ⎫⎪⎪⎝⎭，． 12OG ⎫=⎪⎪⎝⎭，，1SE ⎫=⎪⎪⎝⎭，(AB =． 0SE OG =，0AB OG =，OG 与平面SAB 内两条相交直线SE ，AB 垂直．所以OG ⊥平面SAB ，OG 与DS 的夹角记为α，SD 与平面SAB 所成的角记为β， 则α与β互余．ODBCASD，(DS =．22cos OG DS OG DSα==sin 11β=，所以，直线SD 与平面SAB 所成的角为arcsin ．2．(全国II) 已知正三棱柱111ABC A B C -的侧棱长与底面边长相等，则1AB 与侧面11ACC A 所成角的正弦值等于（）A ．4B．4C ．2D ．2解：已知正三棱柱ABC －A 1B 1C 1的侧棱长与底面边长相等，取A 1C 1的中点D 1，连接BD 1，AD 1，∠B 1AD 1是AB 1与侧面ACC 1A 1所成的角，11sin 4B AD ∠==，选A 。

18.（本小题满分14分）如图6所示，等腰△ABC 的底边AB =66,高CD =3，点E 是线段BD 上异于点B 、D 的动点.点F 在BC 边上，且EF ⊥AB .现沿EF 将△BEF 折起到△PEF 的位置，使PE ⊥AE .记BE x = V (x )表示四棱锥P-ACFE 的体积. （1）求V (x )的表达式；（2）当x 为何值时，V (x )取得最大值？(3）当V (x )取得最大值时，求异面直线AC 与PF 所成角的余弦值2008年广东高考试题（理科）20．（本小题满分14分）如图5所示，四棱锥P ABCD -的底面ABCD 是半径为R 的圆的内接四边形，其中BD 是圆的直径，60ABD ∠=，45BDC ∠=，PD 垂直底面ABCD，PD =，E F ，分别是PB CD ，上的点，且PE DF EB FC=，过点E 作BC的平行线交PC 于G ． （1）求BD 与平面ABP 所成角θ的正弦值； （2）证明：EFG △是直角三角形；（3）当12PE EB =时，求EFG △的面积．FCPG E AB图5D18．（本小题满分１４分）如图６，已知正方体1111ABCD A B C D -的棱长为２，点Ｅ是正方形11BCC B 的中心，点Ｆ、Ｇ分别是棱111,C D AA 的中点．设点11,E G 分别是点Ｅ、Ｇ在平面11DCC D 内的正投影． （１）求以Ｅ为顶点，以四边形FGAE 在平面11DCC D 内 的正投影为底面边界的棱锥的体积；（２）证明：直线11FG FEE ⊥平面；（３）求异面直线11E G EA 与所成角的正弦值2010年广东高考试题（理科）18.（本小题满分14分）如图5，¼ABC 是半径为a 的半圆，AC 为直径，点E 为»AC 的中点，点B 和点C 为线段AD 的三等分点．平面AEC 外一点F 满足FB DF ==，． （1）证明：EB ⊥FD ；（2）已知点Q,R 分别为线段FE,FB 上的点，使得22,33BQ FE FR FB ==,求平面BED 与平面RQD 所成二面角的正弦值．18.(本小题满分13分)如图5.在椎体P-ABCD中，ABCD是边长为1的棱形，==且∠DAB=60︒，PA PDE,F分别是BC,PC的中点.(1) 证明：AD ⊥平面DEF;(2) 求二面角P-AD-B的余弦值.2012年广东高考试题（理科）18.（本小题满分13分）如图5所示，在四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，点 E在线段PC 上，PC⊥平面BDE。

2007年普通高等学校招生全国统一考试（全国1卷）数学（理）试题第Ⅰ卷参考公式：如果事件A B ，互斥，那么球的表面积公式 ()()()P A B P A P B +=+24πS R =如果事件A B ，相互独立，那么其中R 表示球的半径 ()()()P A B P A P B =球的体积公式如果事件A 在一次试验中发生的概率是p ，那么34π3V R =n 次独立重复试验中事件A 恰好发生k 次的概率其中R 表示球的半径()(1)(012)k k n kn n P k C p p k n -=-=，，，…， 一、选择题（1）α是第四象限角，5tan 12α=-，则sin α=（ ） A ．15 B ．15- C ．513 D ．513-（2）设a 是实数，且1i 1i 2a +++是实数，则a =（ ） A ．12 B ．1 C ．32D ．2（3）已知向量(56)=-，a ，(65)=，b ，则a 与b （ ） A ．垂直B ．不垂直也不平行C ．平行且同向D ．平行且反向（4）已知双曲线的离心率为2，焦点是(40)-，，(40)，，则双曲线方程为（ ） A ．221412x y -= B ．221124x y -= C ．221106x y -= D ．221610x y -= （5）设a b ∈R ，，集合{}10ba b a b a ⎧⎫+=⎨⎬⎩⎭，，，，，则b a -=（ ） A ．1B ．1-C ．2D ．2-（6）下面给出的四个点中，到直线10x y -+=的距离为22，且位于1010x y x y +-<⎧⎨-+>⎩，表示的平面区域内的点是（ ）A ．(11)，B ．(11)-，C ．(11)--，D ．(11)-，（7）如图，正四棱柱1111ABCD A BC D -中，12AA AB =，则异面直线1A B 与1AD 所成角的余弦值为（ ）A ．15B ．25C ．35D ．45（8）设1a >，函数()log a f x x =在区间[]2a a ，上的最大值与最小值之差为12，则a =（ ） A ．2B ．2C ．22D ．4（9）()f x ，()g x 是定义在R 上的函数，()()()h x f x g x =+，则“()f x ，()g x 均为偶函数”是“()h x 为偶函数”的（ ） A ．充要条件 B ．充分而不必要的条件C ．必要而不充分的条件D ．既不充分也不必要的条件（10）21nx x ⎛⎫- ⎪⎝⎭的展开式中，常数项为15，则n =（ ）A ．3B ．4C ．5D ．6（11）抛物线24y x =的焦点为F ，准线为l ，经过F 且斜率为3的直线与抛物线在x 轴上方的部分相交于点A ，AK l ⊥，垂足为K ，则AKF △的面积是（ ） A ．4B ．33C ．43D ．8（12）函数22()cos 2cos 2xf x x =-的一个单调增区间是（ ） A ．233ππ⎛⎫ ⎪⎝⎭，B ．62ππ⎛⎫ ⎪⎝⎭，C ．03π⎛⎫ ⎪⎝⎭，D ．66ππ⎛⎫- ⎪⎝⎭，第Ⅱ卷二、填空题：本大题共4小题，每小题5分，共20分．把答案填在横线上．（13）从班委会5名成员中选出3名，分别担任班级学习委员、文娱委员与体育委员，其中AB1B1A1D1C C D甲、乙二人不能担任文娱委员，则不同的选法共有 种．（用数字作答） （14）函数()y f x =的图像与函数3log (0)y x x =>的图像关于直线y x =对称，则()f x = ．（15）等比数列{}n a 的前n 项和为n S ，已知1S ，22S ，33S 成等差数列，则{}n a 的公比为 ． （16）一个等腰直角三角形的三个顶点分别在正三棱柱的三条侧棱上．已知正三棱柱的底面边长为2，则该三角形的斜边长为 ．三、解答题：本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤． （17）（本小题满分10分）设锐角三角形ABC 的内角A B C ，，的对边分别为a b c ，，，2sin a b A =． （Ⅰ）求B 的大小；（Ⅱ）求cos sin A C +的取值范围．（18）（本小题满分12分） 某商场经销某商品，根据以往资料统计，顾客采用的付款期数ξ的分布列为ξ1 2 3 4 5 P0.40.20.20.10.1商场经销一件该商品，采用1期付款，其利润为200元；分2期或3期付款，其利润为250元；分4期或5期付款，其利润为300元．η表示经销一件该商品的利润．（Ⅰ）求事件A ：“购买该商品的3位顾客中，至少有1位采用1期付款”的概率()P A ； （Ⅱ）求η的分布列及期望E η．（19）（本小题满分12分）四棱锥S ABC D -中，底面A B C D 为平行四边形，侧面SBC ⊥底面A B C D ．已知45ABC = ∠，2AB =，22BC =，3SA SB ==．（Ⅰ）证明SA BC ⊥；（Ⅱ）求直线SD 与平面SAB 所成角的大小．（20）（本小题满分12分） 设函数()e e xxf x -=-．DBCAS（Ⅰ）证明：()f x 的导数()2f x '≥；（Ⅱ）若对所有0x ≥都有()f x ax ≥，求a 的取值范围．（21）（本小题满分12分）已知椭圆22132x y +=的左、右焦点分别为1F ，2F ．过1F 的直线交椭圆于B D ，两点，过2F 的直线交椭圆于AC ，两点，且AC BD ⊥，垂足为P ．（Ⅰ）设P 点的坐标为00()x y ，，证明：2200132x y +<； （Ⅱ）求四边形ABCD 的面积的最小值．（22）（本小题满分12分）已知数列{}n a 中12a =，1(21)(2)n n a a +=-+，123n =，，，…． （Ⅰ）求{}n a 的通项公式； （Ⅱ）若数列{}n b 中12b =，13423n n n b b b ++=+，123n =，，，…， 证明：432n n b a -<≤，123n =，，，…．答案解析一、选择题 1.答案：D解析：α是第四象限角，5tan 12α=-，则sin α=－215131tan α=-+ 2.答案：B解析：设a 是实数，112a i i +++=(1)1(1)(1)222a i i a a i-+++-+=是实数，则a =1，选B 。

2007-2014年浙江数学高考——立体几何：简答题1、（2014文）如图，在四棱锥A -BCDE中，平面ABC⊥平面BCDE，∠CDE＝∠BED＝90°，AB＝CD＝2，DE＝BE＝1，AC＝2．(1)证明：AC⊥平面BCDE；(2)求直线AE与平面ABC所成的角的正切值．（2014理）如图，在四棱锥A-BCDE中，平面ABC⊥平面BCDE，∠CDE＝∠BED＝90°，AB＝CD＝2，DE＝BE＝1，AC＝2．(1)证明：DE⊥平面ACD；(2)求二面角B -AD -E的大小．2、（2013文）如图，在四棱锥P-ABCD 中，P A ⊥平面ABCD ，AB =BC =2，AD =CD P A ∠ABC =120°，G 为线段PC 上的点．（1）证明：BD ⊥平面APC ；（2）若G 为PC 的中点，求DG 与平面APC 所成的角的正切值；（3）若G 满足PC ⊥平面BGD ，求PG GC 的值．（2013理）如图,在四面体BCD A -中,⊥AD 平面B C D ,,BC CD ⊥ 2,AD =BD =M 是AD 的中点,P 是BM 的中点,点Q 在线段AC 上,且QC AQ 3=．(1)证明://PQ 平面BCD ;(2)若二面角D BM C --的大小为060,求BDC ∠的大小．3、（2012文）如图，在侧棱垂直底面的四棱柱ABCD-A1B1C1D1中，AD||BC，AD⊥AB，ABAD=2，BC=4，AA1=2，E是DD1的中点，F是平面B1C1E与直线AA1的交点．（1）证明：①EF||A1D1②BA1⊥平面B1C1EF（2）求BC1与平面B1C1EF所成的角的正弦值．（2012理）如图，在四棱锥P-ABCD中，底面是边长为BAD=120°，且P A⊥平面ABCD，P A=，M，N,分别是PB，PD的中点．（1）证明：MN||平面ABCD；（2）过点A作AQ⊥PC，垂足为点Q，求二面角A-MN-Q的平面角的余弦值．4、（2011文）如图，在三棱锥P-ABC中，AB=AC，D为BC的中点，PO⊥平面ABC，垂足O落在线段AD上．（1）证明：AP⊥BC；（2）已知BC=8，PO=4，AO=3，OD=2．求二面角B-AP-C的大小．（2011理）如图，在三棱锥P-ABC中，AB=AC，D为BC的中点，PO⊥平面ABC，垂足O落在线段AD上．已知BC=8，PO=4，AO=3，OD=2．（1）证明：AP⊥BC；（2）在线段AP上是否存在点M，使得二面角A-MC-B为直二面角？若存在，求出AM的长；若不存在，请说明理由．5、（2010文）如图，在平行四边形ABCD中，AB=2BC，∠ABC=120°，E为线段AB的中点，将△ADE沿直线DE翻折成△A’DE，使平面A’DE⊥平面BCD，F为线段A’C的中点．（1）求证：BF||平面A’DE；（2）设M为线段DE的中点，求直线FM与平面A’DE所成角的余弦值．（2010理）如图，在矩形ABCD中，点E，F分别在线段AB，AD上，AE=EB=AF=23FD=4，沿直线EF将△AEF翻折成△A’EF，使平面A’EF⊥平面BEF．（1）求二面角A’-FD-C的余弦值；（2）点M，N分别在线段FD，BC上，若沿直线MN将四边形MNCD向上翻折，使C与A’重合，求线段FM的长．6、（2009文）如图，DC⊥平面ABC，EB//DC，AC=BC=EB=2DC=2，∠ACB=120°，P，Q分别是AE，AB的中点.（1）证明：PQ//平面ACD ;（2）求AD与平面ABE所成角的正弦值.（2009理）如图，平面P AC⊥平面ABC，△ABC是以AC为斜边的等腰直角三角形，E，F，O 分别是P A，PB，AC的中点，AC=16，P A=PC=10.（1）设G是OC的中点，证明：FG//平面BOE；（2）证明：在△ABO内存在一点M，使FM⊥平面BOE，并求点M到OA，OB的距离.7、（2008）如图，矩形ABCD和梯形BEFC所在的平面互相垂直，∠BCF=∠CEF=90°，EF=2.（1）求证：AE//平面DCF；（2）当AB的长为何值时，二面角A-EF-C的大小为60°.8、（2007文）在如图所示的几何体中，EA⊥平面ABC，DB⊥平面ABC，AC⊥BC，且AC=BC=BD=2AE，M是AB的中点.（1）求证：CM⊥EM；（2）求DE与平面EMC所成角的正切值.（2007理）在如图所示的几何体中，EA⊥平面ABC，DB⊥平面ABC，AC⊥BC，且AC=BC=BD=2AE，M是AB的中点.（1）求证：CM⊥EM；（2）求CM与平面CDE所成的角.。

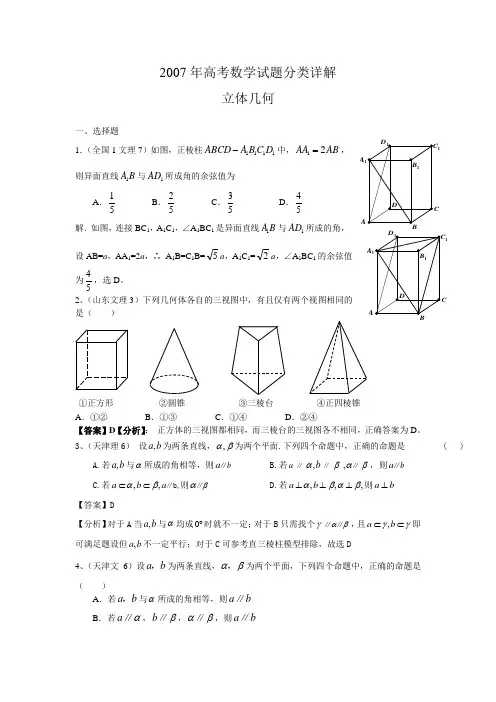
2007年高考数学试题分类详解立体几何一、选择题1．（全国1文理7）如图，正棱柱1111ABC D A B C D -中，12AA AB =，则异面直线1A B 与1AD 所成角的余弦值为A ．15B ．25C ．35D ．45解．如图，连接BC 1，A 1C 1，∠A 1BC 1是异面直线1A B 与1AD 所成的角，设AB=a ，AA 1=2a ，∴ A 1B=C 1B=5a ，A 1C 1=2a ，∠A 1BC 1的余弦值为45，选D 。

2、（山东文理3）下列几何体各自的三视图中，有且仅有两个视图相同的是（ ）A ．①②B．①③C ．①④D．②④【答案】D 【分析】： 正方体的三视图都相同，而三棱台的三视图各不相同，正确答案为D 。

3、（天津理6） 设,a b 为两条直线，,αβ为两个平面.下列四个命题中，正确的命题是 ( )A.若,a b 与α所成的角相等，则b a ∥B.若a∥,b α∥β,α∥β，则b a ∥C.若,,a b a αβ⊂⊂∥b,则βα∥D.若,,,a b αβαβ⊥⊥⊥则a b ⊥【答案】D【分析】对于A 当,a b 与α均成0︒时就不一定；对于B 只需找个γαβ∥∥，且,a b γγ⊂⊂即可满足题设但,a b 不一定平行；对于C 可参考直三棱柱模型排除，故选D4、（天津文6）设a b ，为两条直线，αβ，为两个平面，下列四个命题中，正确的命题是（ ）A ．若a b ，与α所成的角相等，则a b ∥B ．若a α∥，b β∥，αβ∥，则a b ∥DCBAC 1B 1D 1A 1DCBAC 1B 1D 1A 1①正方形 ②圆锥③三棱台 ④正四棱锥C ．若a α⊂，b β⊂，a b ∥，则αβ∥D ．若a α⊥，b β⊥，αβ⊥，则a b ⊥【解析】Ａ项中若a b ，与α所成的角相等，则a b ，可以平行、相交、异面故错；Ｂ项中若a b αβ，∥∥，αβ∥，则a b ，可以平行、异面故错；Ｃ项中若a b ⊂⊂，，αβa b ∥则,αβ可以平行、相交；而D 项是对，因为此时a b ，所成的角与,αβ所成的角是相等或是互补的，则a b ⊥．5、（广东文6）若,,l m n 是互不相同的空间直线，,αβ是不重合的平面，则下列命题中为真命题的是【解析】逐一判除,易得答案(D).6、（全国2理7）已知正三棱柱ABC －A 1B 1C 1的侧棱长与底面边长相等，则AB 1与侧面ACC 1A 1所成角的正弦等于 (A)64(B)104(C)22(D)32解．已知正三棱柱ABC －A 1B 1C 1的侧棱长与底面边长相等，取A 1C 1的中点D 1，连接BD 1，AD 1，∠B 1AD 1是AB 1与侧面ACC 1A 1所成的角，11362sin 42B AD ∠==，选A 。

专题08 立体几何一、选择题1．（全国Ⅰ•理•7题）如图，正四棱柱1111D C B A ABCD -中，AB AA 21=，则异面直线11AD B A 与所成角的余弦值为（ D ）A ．51 B ．52 C ．53 D ．542．（全国Ⅱ•理•7题）已知正三棱柱ABC －A 1B 1C 1的侧棱长与底面边长相等，则AB 1与侧面ACC 1A 1所成角的正弦等于（ A ）A ．BCD 3．（北京•理•3题）平面α∥平面β的一个充分条件是（ D ）A ．存在一条直线a a ααβ，∥，∥B ．存在一条直线a a a αβ⊂，，∥C ．存在两条平行直线a b a b a b αββα⊂⊂，，，，∥，∥D ．存在两条异面直线a b a a b αβα⊂，，，∥，∥4．（安徽•理•2题）设l ，m ，n 均为直线，其中m ，n 在平面α内，“l α⊥”是l m⊥且“l n ⊥”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件7．（福建•理•10题）顶点在同一球面上的正四棱柱ABCD －A 1B 1C 1D 1中，AB ＝1，AA 1＝，则A 、C 两点间的球面距离为（B ）A ．4πB ．2πC D ．9．（湖南•理•8题）棱长为1的正方体1111ABCD A B C D -的8个顶点都在球O 的表面上，E F ，分别是棱1AA ，1DD 的中点，则直线EF 被球O 截得的线段长为（ D ）A B ．1C ．21 D10．（江苏•理•4题）已知两条直线,m n ，两个平面,αβ，给出下面四个命题： ①//,m n m n αα⊥⇒⊥ ②//,,//m n m n αβαβ⊂⊂⇒ ③//,////m n m n αα⇒ ④//,//,m n m n αβαβ⊥⇒⊥ 其中正确命题的序号是（ C ）A ．①③B ．②④C ．①④D ．②③ 11．（江西•理•7题）如图，正方体AC 1的棱长为1，过点A 作平面A 1BD 的垂线，垂足为点H ．则以下命题中，错误．．的命题是（ D ） A ．点H 是△A 1BD 的垂心 B ．AH 垂直平面CB 1D 1C ．AH 的延长线经过点C 1D ．直线AH 和BB 1所成角为45° 12．（辽宁•理•7题）若m n ，是两条不同的直线，αβγ，，是三个不同的平面，则下列命题中的真命题是（ ）A ．若m βαβ⊂⊥，，则m α⊥B ．若m αγ= n βγ= ，m n ∥，则αβ∥C ．若m β⊥，m α∥，则αβ⊥D ．若αγ⊥，αβ⊥，则βγ⊥ 13．（陕西•理•6题）一个正三棱锥的四个顶点都在半径为1的球面上，其中底面的三个顶点在该球的一个大圆上，则该正三棱锥的体积是（ B ）A ．433 B ．33 C ． 43 D ．12314．（四川•理•4题）如图，ABCD -A 1B 1C 1D 1为正方体，下面结论错误．．的是（ D ） A ．BD ∥平面CB 1D 1 B ．AC 1⊥BDC ．AC 1⊥平面CB 1D 1 D ．异面直线AD 与CB 1角为60°15．(宁夏•理•8题) 已知某个几何体的三视图如下，根据图中标出的尺寸（单位：cm ），可得这个几何体的体积是（ B ）Ａ．34000cm 3 Ｂ．38000cm 3Ｃ．32000cmＤ．34000cmＣ．若a b a b αβ⊂⊂，，∥，则αβ∥ Ｄ．若a b αβ⊥⊥，，αβ⊥，则a b ⊥18．（浙江•理•6题）若P 是两条异面直线,l m 外的任意一点，则（ B ）A ．过点P 有且仅有一条直线与,l m 都平行B ．过点P 有且仅有一条直线与,l m都垂直C ．过点P 有且仅有一条直线与,l m 都相交D ．过点P 有且仅有一条直线与,l m都异面二、填空题正视图侧视图俯视图19．（全国Ⅰ•理•16题）一个等腰直角三角形的三个顶点分别在正三棱柱的三条侧棱上。

Using the research method of literature, meansof observation, behavioralapproach, con ceptual an alysis and the patter n of in formati on-seek ing of local and overseas were an alyzed and compared, Basic pattern strategies of tech no logy in formatio n-seeki ng2007年高考数学试题汇编一一立体几何（二）二、填空题19.（全国I ?理?16题）一个等腰直角三角形的三个顶点分别在正三棱柱的三条侧棱上。

已知正三棱柱的底面边长为 2,则该三角形的斜边长为【解答】一个等腰直角三角形 DEF 的三个顶点分别在正三棱柱的三条侧棱上，/EDF=90° ,已知正三棱柱的底面边长为 AB=2，则该三角形的斜边 EF 上的中线 DG= ',20.（全国n ?理?15题）一个正四棱柱的各个顶点在一个直径为 2cm 的球面上。

如果 正四棱柱的底面边长为 1cm ，那么该棱柱的表面积为 _ - ’ 4 J 二 【解答】一个正四棱柱的各个顶点在一个直径为 2cm 的球面上。

正四棱柱的对角线的长为球的直径，现正四棱柱底面边长为 1cm ，设正四棱柱的高为 h ，二2R=2=山■-匸■'解得h= ，那么该棱柱的表面积为 2+4 ” - cm2.21.（安徽？理?15题）在正方体上任意选择 4个顶点，它们可能是如下各种几何形体的4个顶点，这些几何形体是 ____________ （写出所有正确结论的编号）。

cm2。

•••斜边EF①矩形；②不是矩形的平行四边形；③有三个面为等腰直角三角形，有一个面为等边三角形的四面体；④每个面都是等边三角形的四面体；⑤每个面都是直角三角形的四面体。

2007 年高考数学试题分类汇编立体几何一．选择题1． (2007 安徽·文 )设 l , m, n 均为直线 ,此中 m, n 在平面a 内, 则“l ”是 “l”是 “l m 且 l n ”）的（(A) 充足不用要条件 (B) 必需不充足条件 (C) 充足必需条件(D) 既不充足也不用要条件2． (2007 安徽·文 )把边长为2 的正方形 ABCD 沿对角线 AC 折成直二面角 ,折成直二面角后 ,在 A,B,C,D 四点所在的球面上 ,B 与 D 两点之间的球面距离为（）(A) 22(B)(C)(D)233． (2007 北京·文 ) 平面 ∥平面 的一个充足条件是（）Ａ．存在一条直线 ， a ∥ ， a ∥Ｂ．存在一条直线a ， a， a ∥Ｃ．存在两条平行直线Ｄ．存在两条异面直线a ，b ， a ， b ， a ∥ ， b ∥a ，b ， a， a ∥ ， b ∥4．(2007 福建·文 ) 如图，在正方体 ABCD A 1B 1C 1 D 1 中， E ，F ，G ，HD 1C 1A 1HB 1分别为 AA 1 ， AB ， BB 1 ， B 1C 1 的中点，则异面直线 EF 与 GH 所成的角G等于（ ）E DCＡ． 45Ｂ． 60Ｃ． 90 Ｄ． 120AFB5． (2007 广东·文 ) 若 l 、 m 、 n 是互不同样的空间直线， α 、 β 是不重合的平面，则以下命题中为真命题的是（ ）A ．若 // ,l , n，则 l // nB ．若, l ，则 lC. 若 ln, m n ，则 l // mD．若 l,l //，则//6．(2007 湖北· 文 ) 在棱长为 1 的正方体 ABCD A 1B 1C 1 D 1 中， E ，F 分别为棱 AA 1， BB 1 的中 点， G 为棱 A 1B 1 上的一点，且 AG 1(0 ≤ ≤ 1)．则点 G 到平面 D 1EF 的距离为（）Ａ． 3Ｂ．2 25 2Ｃ．Ｄ．357．(2007 天津·文 )设 a ，b 为两条直线，， 为两个平面，以下四个命题中，正确的命题是（ ）A ．若 a ，b 与 所成的角相等，则 a ∥ bB ．若 a ∥ ， b ∥ ， ∥ ，则 a ∥ bC ．若 a， b ， a ∥ b ，则 ∥D ．若 a ， b，，则 a b8 ． (2007湖南·文) 如 图1，在正四棱柱ABCDA 1B 1C 1D 1 中，E ，F 分别是 AB 1 ， BC 1 的中D 1C 1点，则以下结论中不可立 的是（）A 1B 1．．．A ． EF 与 BB 1垂直 B ． EF 与 BD 垂直 E FC ． EF 与 CD 异面D ． EF 与 A 1C 1异面DC9．(2007 江西· 文 ) 四周体 ABCD 的外接球球心在 CD AB上，且 CD2，AD3 ，在外接球面上两点 A ，B 间的球面距离是（）ππ2π5πＡ．Ｂ．Ｃ．Ｄ．633610．(2007 全国Ⅰ· 文 )如图，正四棱柱 ABCD A 1 B 1C 1D 1 中， AA 1 2 AB ，则异面直线 A 1 B与 AD 1 所成角的余弦值为（）D 1C 1A 1Ａ．1234B 1Ｂ．Ｃ．Ｄ． 5555DCAB11．(2007 全国Ⅱ·文 )已知三棱锥的侧棱长的底面边长的 2 倍，则侧棱与底面所成角的余弦值等于（ ）3323A ．B ．C ．D ．642212． (2007 陕西·文 )Rt △ ABC 的三个极点在半径为 13 的球面上，两直角边的长分别为 6 和8，则球心到平面 ABC 的距离是（A ）5（B ）6（C ）10（D ）12(2007 四川·文 )如图， ABCD -A 1B 1C 1D 1 为正方体，下边结论错误 的是．． (A ） BD ∥平面 CB 1D 1 (B) AC1⊥BD(C)AC 1⊥平面 CB 1D 1 (D) 异面直线 AD 与 CB 所成的角为 60°二．填空题13．(2007 天津·文 )一个长方体的各极点均在同一球的球面上，分别为 1， 2 ， 3 ，则此球的表面积为 ．且一个极点上的三条棱的长14． (2007全国Ⅰ·文)正四棱锥SABCD 的底面边长和各侧棱长都为2，点 S ，A ， B ，C ，D 都在同一个球面上，则该球的体积为_________．15． (2007 全国Ⅱ·文 )一个正四棱柱的各个极点在一个直径为2cm 的球面上．假如正四棱柱的底面边长为1cm ，那么该棱柱的表面积为cm 2 ．16．(2007 江西·文 ) 如图，正方体 AC 1 的棱长为 1，过点作平面 A 1 BD 的垂线，垂足为点 H ．有以下四个命题Ａ．点 H 是 △ A 1BD 的垂心Ｂ． AH 垂直平面 CB 1 D 1Ｃ．二面角 C B 1D 1C 1 的正切值为 23 Ｄ．点 H 到平面 A 1B 1C 1D 1 的距离为4此中真命题的代是 ．（写出全部真命题的代）三．解答题17． (2007广东·文 ) 已知某几何体的俯视图是如图5所示的矩形，正视图 ( 或称主 视图 ) 是一个底边长为 8、高为 4的等腰三角形，侧视图 ( 或称左视图 ) 是一个底边长为 6、高为 4的等腰三角形．(1) 求该几何体的体积 V ；(2) 求该几何体的侧面积 S解 : 由已知可得该几何体是一个底面为矩形,高为 4,极点在底面的射影是矩形中心的四棱锥 V-ABCD ;(1)1 8 6464V3(2) 该四棱锥有两个侧面VAD. VBC 是全等的等腰三角形 ,且 BC 边上的高为8 2h 1424 2, 另两个侧面 VAB. VCD 也是全等的等腰三角形 ,22AB 边上的高为h 2426 52所以S 2(164 21 8 5)402422218． (2007 北京·文 ) 如图，在Rt△AOB中，OAB π4 ． Rt△ AOC 可，斜边 AB6以经过 Rt△ AOB 以直线 AO 为轴旋转获得，且二面角 B AO C 的直二面角． D 是 AB 的中点．（ I ）求证：平面COD平面AOB；A（ II ）求异面直线AO 与 CD 所成角的大小．DO B 解法一：C（ I ）由题意，CO AO， BO AO ，BOC 是二面角B AO C 是直二面角，ACO BO ，又AO BO O ，CO 平面 AOB ，又CO 平面 COD．平面 COD平面 AOB ．D（II）作DE OB ，垂足为 E ，连结 CE （如图），则 DE ∥ AO ，CDE 是异面直线 AO 与 CD 所成的角．在 Rt△COE 中， CO BO 2，OE 11 ，BO2ECE CO2OE25．O B又 DE 13 ．C AO2CE515在 Rt△CDE 中， tan CDE3．DE3异面直线 AO 与 CD 所成角的大小为arctan15 ．3解法二：（ I ）同解法一．（ II ）成立空间直角坐标系O xyz，如图，则 O(0，0，0) ，z 3) ， C(2，0，0) ，A(0，0，2D(0，1， 3) ，AOA (0，0，2 3) ， CD( 2，1， 3) ，OA CD Dcos OA ，CDOA CD662 3 2 2．4O6 ． x CBy异面直线 AO 与 CD 所成角的大小为 arccos419． (2007 福建·文 ) 如图，正三棱柱 ABC A 1B 1C 1 的全部棱长都为 2 ， D 为 CC 1中点．（Ⅰ）求证： AB 1 ⊥ 平面 A 1BD ；AA 1（Ⅱ）求二面角A A 1 DB 的大小．CC 1D解法一：（Ⅰ）取 BC 中点 O ，连结 AO ．BB 1△ ABC 为正三角形， AO ⊥ BC ．正三棱柱 ABC A 1B 1C 1 中，平面 ABC ⊥ 平面 BCC 1B 1 ， AO ⊥ 平面 BCC 1 B 1 ．连结 B 1O ，在正方形 BB 1C 1C 中， O ， D 分别为BC ， CC 1 的中点，AA 1B 1O ⊥ BD ，FGAB 1⊥ BD ．CDC 1O在正方形 ABB 1 A 1 中， AB 1 ⊥ A 1B ，BB 1AB 1 ⊥平面 A 1BD ．（Ⅱ）设 AB 1 与 A 1 B 交于点 G ，在平面 A 1 BD 中， 作 GF ⊥ A 1D 于 F ，连结 AF ，由（Ⅰ）得AB 1 ⊥ 平面 A 1BD ．AF ⊥ A 1D ，∠ AFG 为二面角 A A 1 DB 的平面角．4 5在 △ AA 1 D 中，由等面积法可求得 AF 5，又 AG1AB 12 ，2AG2 10sin ∠AFG4 5 ．AF45z所以二面角 A A 1DB 的大小为 arcsin10AA 1．4解法二：（Ⅰ）取 BC 中点 O ，连结 AO ．△ ABC 为正三角形，AO ⊥ BC ．CC 1在正三棱柱 ABCA 1B 1C 1 中，DO O 1yB平面 ABC ⊥ 平面 BCC 1B 1 ，B 1xAO ⊥ 平面 BCC 1B 1 ．取B 1C 1 中点 O 1 ，以 O 为原点， OB ， OO 1 ， OA 的方向为 x ， y ，z 轴的正方向成立空间直角坐标系，则 B(10，，0) ， D ( 11，，0) ， A 1 (0，2，3) ， A(0，0， 3) ， B 1 (12，，0) ，AB(12，， 3) ， BD( 2，1，0) ， BA( 1，2， 3) ．11AB 1 BD 2 2 0 0， AB 1 BA 1 1430，AB 1⊥BD ， AB 1⊥BA 1．AB 1 ⊥平面 A 1BD ．（Ⅱ）设平面 A 1 AD 的法向量为 n (x ， y ， z) ．AD ( 11，， 3) ， AA 1 (0，2，0) ． n ⊥ AD ， n ⊥ AA 1 ，n AD 0，x y 3z 0，y 0，，，．n AA 10 2 y x3z令 z 1得 n(3，0，1) 为平面 A 1AD 的一个法向量．由（Ⅰ）知 AB 1 ⊥ 平面 A 1BD ，AB 1 为平面 A 1 BD 的法向量．cosn ， AB 1n AB 1 3 2 36 ．n AB 1 2 24二面角 A A 1DB 的大小为 arccos 6 ．420． (2007 安徽·文 ) 如图，在三棱锥 V ABC 中，VC ⊥底面 ABC ， AC ⊥BC ，D 是AB 的中点，且 AC BCa ， ∠ VDCπ ．Ｖ2（ I ）求证：平面 VAB ⊥ 平面 VCD ；Ｃ BC 与平面 VAB 所成的角为 π．（ II ）试确立角 的值，使得直线6AＤＢ解法 1：（Ⅰ） ∵ ACBC a ， ∴△ ACB 是等腰三角形，又 D 是 AB 的中点，∴ CD AB ，又 VC 底面 ABC ． ∴VC AB ．于是 AB 平面 VCD ． 又 AB 平面 VAB ，∴平面 VAB 平面 VCD ． （Ⅱ） 过点 C 在平面 VCD 内作 CH VD 于 H ，则由（Ⅰ）知 CD 平面 VAB ． 连结 BH ，于是 CBH 就是直线 BC 与平面 VAB 所成的角．依题意CBHπ6 ，所以在 Rt △CHD 中， CH2a sin ；2在 Rt △ BHC 中， CHπ a ，a sin62∴ sin2．2 ∵ 0π π ，∴．24故当π BC 与平面 VAB 所成的角为π时，直线．46解法 2：（Ⅰ）以 CA ，CB ，CV 所在的直线分别为 x 轴、 y 轴、 z 轴，成立如下图的空间直角坐标系，则，，，，，，， ，， D a a，， 2 a tan，， ， ，C(0 0 0)A(a 0 0)B(0a 0)2 0 V 0 022于是， a a 2 ， CDa a ， AB( a ， a ，0) ．VD， ，a tan2 ， ，02 222进而·， ，· a a121 2 ，即AB CD ．(，，aa 0AB CDaa 0)2 0222同理 ·， ，· a a 21 212，(， ，a tanaaAB VDa a 0) 2 2 222即 ABVD ．又 CD VD D ，∴AB 平面 VCD ．又 AB 平面 VAB ． ∴ 平面 VAB 平面 VCD ．（Ⅱ）设平面 VAB 的一个法向量为n ( x ， y ， z) ，z 则由 n ·AB 0， n ·VD 0 ．Vax ay，得 aa 2．xyaz tan222CB y可取 n(11，， 2 cot )，又 BC(0， a ，0) ，Dπ ·a2 A，x于是 sinn BC2sin6··2n BC 2 2cota即 sin2 ∵ 0π π2 ， ∴ = 4 ．2故友 =π π时，直线 BC 与平面 VAB 所成的角为 6．4解法 3：（Ⅰ）以点 D 为原点，以 DC ， DB 所在的直线分别为x 轴、 y 轴，成立如下图的空间直角坐标系，则，，，， 2 ， ，，2， ， C2，，，D(000) A 02 a 0 B 02 a 0a 0 02V2 ，，2，于是 DV2 ，， 2a tan， DC2，，，2 a 02 a tan2 a 02 a 0 02AB (0， 2a ，0) ．进而 AB ·DC(0， 2a ，0)·2 ，， 0 ，即AB DC ．2 a 0 0同理·， ，2 ，， 2a tan0 ，即 AB DV ．AB DV(0 2a 0)a 022又 DCDVD ，∴AB 平面 VCD ．又 AB 平面 VAB ， ∴ 平面 VAB 平面 VCD ．（Ⅱ）设平面 VAB 的一个法向量为 n ( x ， y ， z) ， 则由 n ·AB 0， n ·DV 0 2ay 0，，得2ax 2az tan22可取 n(tan ，0，1) ，又BC2 ， 2 ， ，2 a 2 a 0π·2a tan 2于是 sin n BC2，2sin6·· 2n BC1 tana 即 sinππ = π，∵ 0，∴ ．22 4故友 π时，4即直线 BC 与平面 VAB 所成角为π．621． (2007 湖南·文 ) 如图 3，已知直二面角PQ0．VCyBDAx，APQ ，B ，C，CA CB ， BAP 45 ，直线 CA 和平面所成的角为 30 ．（I ）证明 BC ⊥ PQ ；（ II ）求二面角B AC P 的大小．CP AQB解：（I ）在平面内过点 C 作 CO ⊥ PQ 于点 O ，连结 OB ．由于⊥，PQ ，所以 CO ⊥，又由于 CACB ，所以 OA OB ．而BAO45 ，所以ABO45 ， AOB 90 ，进而 BO ⊥ PQ ，又 CO ⊥ PQ ，所以 PQ ⊥ 平面 OBC ．由于 BC平面 OBC ，故 PQ ⊥ BC ．（ II ）解法一：由（ I ）知， BO ⊥ PQ ，又⊥，PQ，BO，所以BO ⊥．过点 O 作 OH ⊥ AC 于点 H ，连结 BH ，由三垂线定理知，BH⊥AC ．故 BHO 是二面角 B AC P 的平面角．由（ I ）知， CO ⊥，所以CAO 是 CA 和平面所成的角，则CAO30 ，不如设 AC2，则 AO3， OHAO sin 30 3．2在 Rt △OAB 中，ABO BAO 45 ，所以 BO AO3 ，于是在 Rt △ BOH 中， tanBHOBO 3 2 ．OH32故二面角 BAC P 的大小为 arctan2 ．解法二：由（ I ）知， OC ⊥ OA ， OC ⊥ OB ， OA ⊥ OB ，故能够 O 为原点，分别以直线 OB ，OA ，OC 为 x 轴， y 轴， z 轴成立空间直角坐标系（如图） ．由于 CO ⊥ a ，所以 CAO 是 CA 和平面所成的角，则CAO 30 ．不如设AC 2 ，则 AO3 ，CO ．1在 Rt △OAB 中，ABOBAO 45 ，Cz所以 BOAO3 ．PAB OQ则有关各点的坐标分别是yxO(0，0，0) ， B( 3，0，0) ， A(0， 3，0) ， C (0，01)， ．所以AB ( 3，3，0) ， AC (0， 31)， ．设 n 1{ x ， y ， z} 是平面 ABC 的一个法向量，由n 1 AB 0，3x3 y 0，n 1得AC3y z 0取 x 1，得，， ．(11 3)n 1易知 n 2 (10，，0) 是平面 的一个法向量．设二面角 BAC P 的平面角为，由图可知，， ．n 1 n 2所以 cosn 1 n 2 1 5 ．| n 1 | | n 2 |5 15故二面角 B AC P 的大小为arccos 5．522． (2007 江苏 )如图，已知ABCD A1 B1C1D1是棱长为3的正方体，点 E 在AA1上，点 F 在 CC1上，且 AE FC11，（1）求证：E, B, F , D1四点共面；（4 分）（2）若点G在BC上，BG 2BF ，垂足为 H ，求证： EM ，点 M 在BB1上， GM3面BCC1 B1；（4分）（ 3）用表示截面EBFD1和面 BCC1B1所成锐二面角大小，求tan。

10.立体几何(2007年高考广东卷第12小题)如果一个凸多面体是n 棱锥,那么这个凸多面体的所有顶点所确定的直线共有 条.这些直线中共有()f n 对异面直线,则(4)f =()f n = (答案用数字或n 的解析式表示)【解释】21(1)2n n n C ++=；12；21(1)(2)2n n n n n C ---⋅= (2007年高考广东卷第19小题)如图6所示,等腰ABC ∆的底边AB =高3CD =,点E 是线段BD 上异于B 、D 的动点.点F 在边BC 上,且EF AB ⊥.现沿EF 将BEF ∆ 折起到PEF ∆的位置，使PE AE ⊥。

记BE x =,()V x 表示四棱锥P ACFE -的体积(1)求()V x 的表达式；(2)当x 为何值时，()V x 取得最大值？(3) 当()V x取得最大值时，求异面直线AC 与PF 所成角的余弦值.解：（1）,,EF AB PE EF ⊥∴⊥又,PE AE AEEF E ⊥=， PE ∴⊥平面ACFE 且PE x =，ACDBEF EF x x ∆∆∴==，四棱锥P ACFE -的底面积为22)s x x ==-，1()3V x s PE ∴=⋅231))3xx x x =-=-(0x <<（2）'2())V x x =-，(0,6)x ∈时'()0V x >，x ∈时'()0V x <，()V x 在(0,6)上增，在上减，故()V x 在6x =时，取最大值为（3）过F 作FG AC 交AB 于G ，则PFG ∠是直线AC 与PF 所成角且FGB∆图6AB是等腰三角形，由（2）知6,EF FG FB EG EB PG PF =∴======在2224242721cos 2847PF FG PG PFG PFG PF FG ∆+-+-∠===⋅，所以异面直线AC 与PF 所成角的余弦值为17(2008年高考广东卷第5小题)将正三棱柱截去三个角（如图1所示A B C ，，分别是GHI △三边的中点）得到几何体如图2，则该几何体按图2所示方向的侧视图（或称左视图）为（ A ）【解析】解题时在图2的右边放扇墙(心中有墙),可得答案A. (2008年高考广东卷第20小题)如图5所示，四棱锥P ABCD -的底面ABCD 是半径为R 的圆的内接四边形，其中BD 是圆的直径，60ABD ∠=，45BDC ∠=，PD 垂直底面A B C D，PD =，E F ，分别是PB CD ，上的点，且PE DFEB FC=，过点E 作BC 的平行线交PC 于G ．（1）求BD 与平面ABP 所成角θ的正弦值；（2）证明：EFG △是直角三角形；（3）当12PE EB =时，求EFG △的面积．【解析】（1）在Rt BAD ∆中，60ABD ∠=，,AB R AD ∴== 而PD 垂直底面ABCD ，PA ===PB ===,在PAB ∆中，222PA AB PB +=,即PAB ∆为以PAB ∠为直角的直角三角形。

专题 立体几何 空间向量与立体几何答案部分1．（2018全国卷Ⅰ）【解析】(1)由已知可得，BF ⊥PF ，BF ⊥EF ，所以BF ⊥平面PEF ．又BF ⊂平面ABFD ，所以平面PEF ⊥平面ABFD ． (2)作PH ⊥EF ，垂足为H ．由(1)得，PH ⊥平面ABFD ．以H 为坐标原点，HF u u u r的方向为y 轴正方向，||BF uuu r 为单位长，建立如图所示的空间直角坐标系-H xyz ．由(1)可得，DE ⊥PE ．又DP =2，DE =1，所以PE又PF =1，EF =2，故PE ⊥PF ．可得=PH ,32=EH ． 则(0,0,0)H，P ，3(1,,0)2--D，3(1,2=u u u r DP ， (0,0,)2HP =u u u r 为平面ABFD 的法向量．设DP 与平面ABFD 所成角为θ，则3sin ||4||||HP DP HP DP θ⋅===⋅u u u r u u u ru u u r u u u r ．所以DP 与平面ABFD． 2．(2018全国卷Ⅱ)【解析】(1)因为4AP CP AC ===，O 为AC 的中点，所以OP AC ⊥，且OP =连结OB．因为2AB BC AC ==，所以ABC △为等腰直角三角形， 且OB AC ⊥，122OB AC ==． 由222OP OB PB +=知PO OB ⊥．由⊥OP OB ，⊥OP AC 知PO ⊥平面ABC ．(2)如图，以O 为坐标原点，OB uu u r的方向为x 轴正方向，建立空间直角坐标系O xyz -．A由已知得(0,0,0)O ，(2,0,0)B ，(0,2,0)-A ，(0,2,0)C，(0,0,P ，=AP u u u r，取平面PAC 的法向量(2,0,0)OB =u u u r ． 设(,2,0)(02)-<≤M a a a ，则(,4,0)AM a a =-u u u r．设平面PAM 的法向量为(,,)x y z =n ．由0,0AP AM ⋅=⋅=uu u r uuu r n n得20(4)0y ax a y ⎧+=⎪⎨+-=⎪⎩，可取,)a a =--n ，所以cos ,OB =uu u rn．由已知得|cos ,|OB =uu u r n ．2．解得4a =-（舍去），43a =．所以4()3=-n．又(0,2,PC =-u u u r，所以cos ,PC =uu u r n ． 所以PC 与平面PAM所成角的正弦值为4． 3．（2018全国卷Ⅲ）【解析】(1)由题设知，平面CMD ⊥平面ABCD ，交线为CD ．因为BC ⊥CD ，BC ⊂平面ABCD ，所以BC ⊥平面CMD ，故BC ⊥DM ．因为M 为»CD上异于C ，D 的点，且DC 为直径，所以 DM ⊥CM ． 又BC I CM =C ，所以DM ⊥平面BMC ． 而DM ⊂平面AMD ，故平面AMD ⊥平面BMC ．(2)以D 为坐标原点，DA u u u r的方向为x 轴正方向，建立如图所示的空间直角坐标系D xyz -．当三棱锥M ABC -体积最大时，M 为»CD的中点． 由题设得(0,0,0)D ，(2,0,0)A ，(2,2,0)B ，(0,2,0)C ，(0,1,1)M ，(2,1,1)AM =-u u u u r ，(0,2,0)AB =u u u r ，(2,0,0)DA =u u u r设(,,)x y z =n 是平面MAB 的法向量，则0,0.AM AB ⎧⋅=⎪⎨⋅=⎪⎩u u u u r u u ur n n 即20,20.x y z y -++=⎧⎨=⎩ 可取(1,0,2)=n ．DA u u u r是平面MCD 的法向量，因此cos ,5||||DA DA DA ⋅==u u u ru u u r u u u r n n n ，sin ,5DA =u u u r n ，所以面MAB 与面MCD所成二面角的正弦值是5． 4．（2017新课标Ⅰ）【解析】（1）由已知90BAP CDP ∠=∠=︒，得AB ⊥AP ，CD ⊥PD ．由于AB ∥CD ，故AB ⊥PD ，从而AB ⊥平面P AD ． 又AB ⊂平面P AB ，所以平面P AB ⊥平面P AD ． （2）在平面PAD 内做PF AD ⊥，垂足为F ，由（1）可知，AB ⊥平面PAD ，故AB PF ⊥，可得PF ⊥平面ABCD ．以F 为坐标原点，FA u u u r的方向为x 轴正方向，||AB uuu r 为单位长，建立如图所示的空间直角坐标系F xyz -．由（1）及已知可得2A，(0,0,2P，,1,0)2B，(2C -．所以(,1,)22PC =--u u u r，CB =u u u r，)22PA =-u u u r ， (0,1,0)AB =u u u r．设(,,)x y z =n 是平面PCB 的法向量，则00PC CB ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u ur n n，即0220x y z ⎧-+-=⎪=，可取(0,1,=-n ．设(,,)x y z =m 是平面PAB 的法向量，则00PA AB ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u r m m，即0220x z y -=⎪⎨⎪=⎩， 可取(1,0,1)=n ．则cos ,||||3⋅==-<>n m n m n m ， 所以二面角A PB C --的余弦值为 5．（2017新课标Ⅱ）【解析】（1）取PA 的中点F ，连结EF ，BF ．因为E 是PD 的中点，所以EF AD ∥，12EF AD =．由90BAD ABC ∠=∠=o 得BC AD ∥，又12BC AD =，所以EF BC ∥，四边形BCEF 是平行四边形，CE BF ∥，又BF ⊂平面PAB ，CE ⊄平面PAB ，故CE ∥平面PAB ．（2）由已知得BA AD ⊥，以A 为坐标原点，AB u u u r的方向为x 轴正方向，||AB uuu r 为单位长，建立如图的空间直角坐标系A xyz -，则(0,0,0)A ，(1,0,0)B ，(1,1,0)C，P，(1,0,PC =u u u r ，(1,0,0)AB =u u u r．x设(,,)M x y z (01)x <<，则(1,,)BM x y z =-u u u u r，(,1,PM x y z =-u u u u r．因为BM 与底面ABCD 所成的角为45o，而(0,0,1)=n 是底面ABCD 的法向量，所以|cos ,|sin 45BM <>=ou u u u r n2=， 即222(1)0x y z -+-=． ①又M 在棱PC 上，设PM PC λ=u u u u r u u u r，则x λ=，1y =，z =． ②由①，②解得121x y z ⎧=+⎪⎪⎪=⎨⎪⎪=⎪⎩（舍去），121x y z ⎧=-⎪⎪⎪=⎨⎪⎪=⎪⎩所以(12M -，从而(12AM =-u u u u r ． 设000(,,)x y z =m 是平面ABM 的法向量，则0=0AM AB ⎧⋅=⎪⎨⋅⎪⎩u u u u ru u ur m m，即0000(2200x y x ⎧+=⎪⎨=⎪⎩，所以可取(0,2)=m，于是cos ,||||⋅<>==m n m n m n因此二面角M AB D --的余弦值为5． 6．（2017新课标Ⅲ）【解析】（1）由题设可得，ABD CBD ∆≅∆，从而AD DC =．又ACD ∆是直角三角形，所以0=90ACD ∠取AC 的中点O ，连接DO ，BO ，则DO AC ⊥，DO AO =． 又由于ABC ∆是正三角形，故BO AC ⊥． 所以DOB ∠为二面角D AC B --的平面角． 在Rt AOB ∆中，222BO AO AB +=．又AB BD =，所以222222BO DO BO AO AB BD +=+==，故90DOB ∠=o ． 所以平面ACD ⊥平面ABC ．（2）由题设及（1）知，OA,OB,OD 两两垂直，以O 为坐标原点，OA u u u r的方向为x 轴正方向，OA u u u r为单位长，建立如图所示的空间直角坐标系O xyz -，则(1,0,0)A，B ，(1,0,0)C -，(0,0,1)D ．由题设知，四面体ABCE 的体积为四面体ABCD 的体积的12，从而E 到平面ABC 的距离为D 到平面ABC 的距离的12，即E 为DB的中点，得1(0,)22E ．故(1,0,1)AD =-u u u r ，(2,0,0)AC =-u u u r，1(1,)22AE =-u u u r设()=x,y,z n 是平面DAE 的法向量，则AD AE ⎧=⎪⎨=⎪⎩u u u r g u u u r g 0，0，n n即x z x y z -+=⎧⎪⎨-++=⎪⎩01022可取=n 设m 是平面AEC 的法向量，则0，0，AC AE ⎧=⎪⎨=⎪⎩u u u r g u u u rg m m同理可得(0,=-m则cos ,==g 7n m n m n m 所以二面角D AE C --的余弦值为77．（2016全国I ）【解析】（Ⅰ）由已知可得AF DF ⊥，AF FE ⊥，所以AF ⊥平面EFDC ．又AF ⊂平面ABEF ，故平面ABEF ⊥平面EFDC ．（Ⅱ）过D 作DG EF ⊥，垂足为G ，由（Ⅰ）知DG ⊥平面ABEF ．以G 为坐标原点，GF u u u r 的方向为x 轴正方向，||GF uuu r为单位长度，建立如图所示的空间直角坐标系G xyz -．由（Ⅰ）知DFE ∠为二面角D AF E --的平面角，故60DFE ∠=o，则2DF =，DG =，可得(1,4,0)A ，(3,4,0)B -，(3,0,0)E -，D ．由已知，AB EF ∥，所以AB ∥平面EFDC ．又平面ABCD I 平面EFDC DC =，故AB CD ∥，CD EF ∥．由BE AF ∥，可得BE ⊥平面EFDC ，所以CEF ∠为二面角C BE F --的平面角，60CEF ∠=o．从而可得(C -．所以EC =u u u r ，(0,4,0)EB =u u u r，(3,AC =--u u u r ，(4,0,0)AB =-u u u r．设(),,n x y z =r是平面BCE 的法向量，则C 00n n ⎧⋅E =⎪⎨⋅EB =⎪⎩u u u r r u u u r r，即040x y ⎧+=⎪⎨=⎪⎩，所以可取(3,0,n =r．设m r 是平面CD AB 的法向量，则C 0m m ⎧⋅A =⎪⎨⋅AB =⎪⎩u u u r r u u u rr ，同理可取()4m =r．则cos ,19n m n m n m ⋅==-r r r r r r ．故二面角C E-B -A的余弦值为19-．8．（2016全国II ）【解析】（I ）证明：∵54AE CF ==， ∴AE CFAD CD=，∴EF AC ∥． ∵四边形ABCD 为菱形， ∴AC BD ⊥，∴EF BD ⊥， ∴EF DH ⊥，∴EF D H '⊥． ∵6AC =，∴3AO =；又5AB =，AO OB ⊥，∴4OB =， ∴1AEOH OD AO=⋅=，∴3DH D H '==， ∴222'OD OH D H '=+，∴'D H OH ⊥． 又∵OH EF H =I ，∴'D H ⊥面ABCD ．（Ⅱ）建立如图坐标系H xyz -．()500B ，，，()130C ，，，()'003D ，，，()130A -，，， ()430AB =uu u r ，，，()'133AD =-uuur ，，，()060AC =uuu r，，， 设面'ABD 法向量()1n x y z =，，u r，由1100n AB n AD ⎧⋅=⎪⎨'⋅=⎪⎩u u r u u u r u u r u u u u r得430330x y x y z +=⎧⎨-++=⎩，取345x y z =⎧⎪=-⎨⎪=⎩，∴()1345n =-u r ，，． 同理可得面'AD C 的法向量()2301n =u u r，，， ∴12129575cos 5210n n n n θ⋅+==⋅u r u u ru r u u r ，∴295sin θ． 9．（2016全国III ）【解析】（Ⅰ）由已知得232==AD AM ， 取BP 的中点T ，连接TN AT ,． 由N 为PC 中点知BC TN //，221==BC TN ． 又BC AD //，故TN 平行且等于AM ，四边形AMNT 为平行四边形，于是AT MN //．因为⊂AT 平面PAB ，⊄MN 平面PAB ，所以//MN 平面PAB ．（Ⅱ）取BC 的中点E ，连结AE ，由AC AB =得BC AE ⊥，从而AD AE ⊥， 且5)2(2222=-=-=BC AB BE AB AE ． 以A 为坐标原点，AE u u u r的方向为x 轴正方向，建立如图所示的空间直角坐标系xyz A -，由题意知，)4,0,0(P ，)0,2,0(M ，)0,2,5(C ，)2,1,25(N ， (0,2,4)PM =-u u u u r ，)2,1,25(-=PN ，)2,1,25(=AN ． 设(,,)x y z =r n 为平面PMN 的法向量，则00PM PN ⎧⋅=⎪⎨⋅=⎪⎩r u u u u r r u u u rn n ，即⎪⎩⎪⎨⎧=-+=-0225042z y x z x ， 可取(0,2,1)n =r，于是||85|cos ,|||||n AN n AN n AN ⋅<>==r u u u rr u u u r r u u u r ．10．（2015新课标Ⅰ）【解析】（Ⅰ）连接BD ，设BD AC G =I ，连接,,EG FG EF ．在菱形ABCD 中，不妨设1GB =，由120∠=oABC ，可得3AG GC =由⊥BE 平面ABCD ，AB BC =可知，AE EC =， 又∵⊥AE EC ，∴3EG =，⊥EG AC ，在Rt EBG ∆中，可得2BE 22DF =．在Rt FDG ∆中，可得62FG =．在直角梯形BDFE 中，由2BD =，BE =2DF =，可得2EF =， ∴222EG FG EF +=，∴EG ⊥FG ， ∵AC ∩FG =G ，∴EG ⊥平面AFC ，∵EG ⊂面AEC ，∴平面AFC ⊥平面AEC ．（Ⅱ）如图，以G 为坐标原点，分别以,GB GC u u u r u u u r 的方向为x 轴，y 轴正方向，||GB u u u r为单位长度，建立空间直角坐标系G-xyz ，由（Ⅰ）可得A (0，0)，E(1,0,)，F (－1,0，C (00)， ∴AE u u u r =（1），CF uuu r =（－12）．故cos ,3||||<>==-u u u r u u u ru u u r u u u r g u u u r u u u r AE CF AE CF AE CF ．所以直线AE 与CF所成的角的余弦值为3． 11．（2015新课标II ）【答案】（Ⅰ）详见解析；． 【解析】（Ⅰ）交线围成的正方形EHGF 如图：（Ⅱ）作EM AB ⊥，垂足为M ，则14AM A E ==，18EM AA ==，因为EHGF 为正方形，所以10EH EF BC ===．于是6MH ==，所以10AH =．以D为坐标原点，DA u u u r的方向为x 轴的正方向，建立如图所示的空间直角坐标系D xyz -，则(10,0,0)A ，(10,10,0)H ，(10,4,8)E ，(0,4,8)F ，(10,0,0)FE =u u u r ，(0,6,8)HE =-u u u r．设(,,)n x y z =r 是平面EHGF 的法向量，则0,0,n FE n HE ⎧⋅=⎪⎨⋅=⎪⎩r u u u rr u u u r即100,680,x y z =⎧⎨-+=⎩所以可取(0,4,3)n =r ．又(10,4,8)AF =-u u u r，故cos ,n AF n AF n AF⋅<>==⋅r u u u r r u u u r r u u u r ．所以直线AF 与平面α所成角的正弦值为4515． 【考点定位】1、直线和平面平行的性质；2、直线和平面所成的角．A 1AB 1BD 1DC 1CF E H GM12．(2014新课标1)【解析】（Ⅰ）连接1BC ，交1B C O 于点，连接AO ，因为侧面11BB C C 为菱形，所以1111,B C BC O B C BC ⊥且为及的中点. 又11,.AB B C B C ABO ⊥⊥所以平面1AO ABO B C AO ⊂⊥由于平面，故又11,=.B O CO AC AB =故（Ⅱ）因为11,.AC AB O B C AO CO ⊥=且为的中点，所以 又因为,AB BC BOA BOC =∆≅∆所以，1,,,OA OB OA OB OB ⊥故从而两两相互垂直，以O OB x OB 为坐标原点，的方向为轴正方向，为单位长， O xyz =建立如图所示的空间直角坐标系．zyO因为1160,.CBB CBB AB BC∠=︒∆=所以为等边三角形又，则111111(00(100),(0,(0,,(1,0,(1,,0),3333A B B CAB A B AB B C BC=-==-==--u u u r u u u u r u u u r u u u u r u u u r，，11111(,,)=00,330,0.x y z AA By zABA Bx z=-⎧⋅=⎪⎪⎨⎨⋅=⎪⎪⎩=⎪⎩=u u u ru u u u r设是平面的法向量，则，即所以可取nnnn11111110,0,(1,A BA B CB Cm⎧⋅=⎪⎨⋅=⎪⎩=u u u u ru u u u r设是平面的法向量，则同理可取mmm则1cos,.7⋅==n mn mn m1111.7A AB C--所以二面角的余弦值为13．（2014新课标2）【解析】（Ⅰ）连接BD交AC于点O，连结EO．因为ABCD为矩形，所以O为BD的中点．又E为PD的中点，所以EO∥PB．EO⊂平面AEC,PB⊄平面AEC，所以PB∥平面AEC．（Ⅱ）因为PA⊥平面ABCD，ABCD为矩形，所以AB，AD，AP两两垂直．如图，以A为坐标原点，ABu u u r的方向为x轴的正方向，APu u u r为单位长，建立空间直角坐标系A xyz-，则D1(0,),22E1(0,)22AE=u u u r．设(,0,0)(0)Bm m>，则(C m(AC m=u u u r．设1(,,)x y z=n为平面AEC的法向量，则110,0,ACAE⎧⋅=⎪⎨⋅=⎪⎩uu u ru u u rnn即0,10,22mxy z⎧+=+=⎪⎩，可取1=-n．又2(1,0,0)=n为平面DAE的法向量，由题设121cos,2=n n12=，解得32m=．因为E为PD的中点，所以三棱锥EACD-的高为12．三棱锥E ACD-的体积11313222V=⨯⨯=．14．（2013新课标Ⅰ）【解析】（Ⅰ）取AB中点E，连结CE，1A B，1A E，∵AB=1AA，1BAA∠=060，∴1BAA∆是正三角形，∴1A E⊥AB，∵CA=CB，∴CE⊥AB，∵1CE A E⋂=E，∴AB⊥面1CEA，∴AB⊥1A C；（Ⅱ）由（Ⅰ）知EC ⊥AB ，1EA ⊥AB ，又∵面ABC ⊥面11ABB A ，面ABC ∩面11ABB A =AB ，∴EC ⊥面11ABB A ，∴EC ⊥1EA ，∴EA ，EC ，1EA 两两相互垂直，以E 为坐标原点，EA u u u r 的方向为x 轴正方向，|EA u u u r|为单位长度，建立如图所示空间直角坐标系O xyz -，有题设知A (1,0,0),1A 3,0),C 3B (－1,0,0),则BC uuu r=（1,03,1BB u u u r =1AA u u u r =(－31AC u u u r=(0,33), 设n =(,,)x y z 是平面11CBB C 的法向量，则100BC BB ⎧•=⎪⎨•=⎪⎩u u u ru u u r n n ，即3030x z x ⎧=⎪⎨=⎪⎩，可取n =3，1，-1）， ∴1cos ,AC u u u r n =11|AC AC •u u u ru u u r n |n ||105， ∴直线A 1C 与平面BB 1C 1C 所成角的正弦值为105． 15．（2013新课标Ⅱ）【解析】（Ⅰ）连结1AC ，交1A C 于点O ，连结DO ，则O 为1AC 的中点，因为D 为AB 的中点，所以OD ∥1BC ，又因为OD ⊂平面1A CD ，1BC ⊄平面1A CD ，所以1BC //平面1A CD ；（Ⅱ）由1AA =AC=CB=22AB 可设：AB=2a ，则1AA 2a ，所以AC⊥BC，又因为直棱柱，所以以点C为坐标原点，分别以直线CA、CB、1CC为x轴、y轴、z轴，建立空间直角坐标系如图，1则(0,0,0)C、1)A、D、E，1)CA=u u u r，,,0)22CD=u u u r，,)2CE=u u u r，1(,)2A E=-u u u r，设平面1A CD的法向量为(,,)n x y z=r，则0n CD⋅=r u u u r且1n CA⋅=r u u u r，可解得y x z=-=，令1x=，得平面1A CD的一个法向量为(1,1,1)n=--r，同理可得平面1A CE的一个法向量为(2,1,2)m=-ur，则cos,n m<>=r u r3，所以sin,3n m<>=r u r，所以二面角D-1A C-E的正弦值为316．（2012新课标）【解析】（Ⅰ）在Rt DAC∆中，AD AC=，得：45ADC︒∠=同理：1114590A DC CDC︒︒∠=⇒∠=得：111,DC DC DC BD DC⊥⊥⇒⊥面1BCD DC BC⇒⊥（Ⅱ）11,DC BC CC BC BC⊥⊥⇒⊥面11ACC A BC AC⇒⊥取11A B的中点O，过点O作OH BD⊥于点H，连接11,C O C H1111111AC B C C O A B =⇒⊥，面111A B C ⊥面1A BD 1C O ⇒⊥面1A BD 1OH BD C H BD ⊥⇒⊥ 得：点H 与点D 重合且1C DO ∠是二面角11C BD A --的平面角 设AC a =，则122aC O =，1112230C D a C O C DO ︒==⇒∠= 既二面角11C BD A --的大小为30︒17．（2011新课标）【解析】（Ⅰ）因为60,2DAB AB AD ∠=︒=， 由余弦定理得3BD AD =从而222BD AD AB +=，故BD ⊥AD 又PD ⊥底面ABCD ，可得BD ⊥PD 所以BD ⊥平面P AD ． 故 P A ⊥BD（Ⅱ）如图，以D 为坐标原点，AD 的长为单位长，射线DA 为x 轴的正半轴建立空间直角坐标系D-xyz ，则()1,0,0A ，()03,0B ，，()3,0C -，()0,0,1P ．(3,0),3,1),(1,0,0)AB PB BC =-=-=-uu u v uu v uu u v设平面PAB 的法向量为(,,)x y z =n ，则0AB PB ⎧⋅=⎪⎨⋅=⎪⎩uu u r uu r n n ，即 3030x z ⎧-+=⎪⎨-=⎪⎩因此可取n =3,1,3)设平面PBC的法向量为m，则PBBC⎧⋅=⎪⎨⋅=⎪⎩uu ruu u rmm可取m=（0，-1，3-）27cos,27==-m n故二面角A-PB-C的余弦值为277-．18．（2010新课标）【解析】：以H为原点，,,HA HB HP分别为,,x y z轴，线段HA的长为单位长，建立空间直角坐标系如图，则(1,0,0),(0,1,0)A B（Ⅰ）设(,0,0),(0,0,)(0,0)C m P n m n<>，则1(0,,0),(,,0).22mD m E可得1(,,),(,1,0).22mPE n BC m=-=-因为0022m mPE BC⋅=-+=，所以PE BC⊥（Ⅱ）由已知条件可得331,33m n C=-=-故(313(0,(,(0,0,1)326D E P--设(,,)n x y x=为平面PEH的法向量则0,0,HEHP⎧⋅=⎪⎨⋅=⎪⎩nn即132x yz⎧-=⎪⎨⎪=⎩因此可以取3,0)=n，由(1,0,1)PA=-u u u r，可得2cos,4PA=u u u rn，．所以直线PA与平面PEH所成角的正弦值为4。

2007年高考中的“立体几何初步 （一）空间直线和平面”试题汇编大全一、选择题： 1. (2007安徽理)设l,m,n 均为直线，其中m,n 在平面α内，“l ⊥α”是l ⊥m 且“l ⊥n ”的（ A ）（A ）充分不必要条件 （B ）必要不充分条件(C)充分必要条件 （D ）既不充分也不必要条件2.(2007安徽文)把边长为2的正方形ABCD 沿对角线AC 折成直二面角,折成直二面角后,在A,B,C,D 四点所在的球面上,B 与D 两点之间的球面距离为（ C ） (A)22π(B)π(C)2π(D) 3π3.(2007安徽理)半径为1的球面上的四点D C B A ,,,是正四面体的顶点，则A 与B 两点间的球面距离为（ C ） （A ）)33arccos(-（B ）)36arccos(- （C ）)31arccos(- （D ）)41arccos(-4.（2007福建文)如图，在正方体ABCD-A1B1C1D1中，E 、F 、G 、H 分别为AA1、AB 、BB1、BC1的中点，则异面直线EF 与GH 所成的角等于（ B ）A.45° B .60° C.90° D.120°5（2007福建文、理)已知m 、n 为两条不同的直线，为两个不同的平面，则下列命题中正确的是（ D ） A B C D6.(2007广东文)若,,l m n是互不相同的空间直线，,αβ是不重合的平面，则下列命题中为真命题的是（ D ）【解析】逐一判除,易得答案(D).7.（2007湖北文）在棱长为1的正方体ABCD －A1B1C1D1中，E 、F 分别为棱AA1、BB1的中点，G 为棱A1B1上的一点，且A1G=λ （0≤λ≤1），则点G 到平面D1EF 的距离为（ D ） A.3B.22C.32λ D.558.（2007湖北理）平面α外有两条直线m 和n ，如果m 和n 在平面α内的射影分别是m ＇和n ＇，给出下列四个命题：①m ＇⊥n ＇⇒m ⊥n; ②m ⊥n ⇒ m ＇⊥n ＇ ③m ＇与n ＇相交⇒m 与n 相交或重合； ④m ＇与n ＇平行⇒m 与n 平行或重合.其中不正确的命题个数是（ D ）A.1B.2C.3D.4 9．（2007湖南文）如图1，在正四棱柱 1111ABCD A B C D -中，E 、F 分别是11AB C 、B 的中点，则以下结论中不成立的是( D )A ．1EF BB 与垂直 B. EF BD 与垂直C. EF 与CD 异面D. EF 11与A C 异面 10．（2007湖南理）棱长为1的正方体1111ABCD A B C D -的8个顶点都在球O 的表面上，E F ，分别是棱1AA ，1DD 的中点，则直线EF 被球O 截得的线段长为（ D ） A．2B ．1 C．12+D11．（2007江苏）已知两条直线,m n ，两个平面,αβ，给出下面四个命题：（C ）①//,m n m n αα⊥⇒⊥ ②//,,//m n m n αβαβ⊂⊂⇒ ③//,////m n m n αα⇒ ④//,//,m n m n αβαβ⊥⇒⊥其中正确命题的序号是A ．①③B ．②④C ．①④D ．②③ 12．（2007辽宁文、理）若m n ，是两条不同的直线，αβγ，，是三个不同的平面，则下列命题中的真命题是（ B ）A ．若m βαβ⊂⊥，，则m α⊥B ．若m β⊥，m α∥，则αβ⊥C ．若αγ⊥，αβ⊥，则βγ⊥D ．若m αγ=，n βγ=，m n ∥，则αβ∥13.（2007陕西文、理）已知P 为平面a 外一点，直线l ⊂a,点Q ∈l,记点P 到平面a 的距离为a,点P 到直线l 的距离为b ，点P 、Q 之间的距离为c ，则（ Ａ ）（A ）c b a ≤≤ （B ）c b a ≤≤ (C)b c a ≤≤ (D)a c b ≤≤14.（2007四川文、理）如图，ABCD-A1B1C1D1为正方体，下面结论错误的是（ D ）(A ）BD ∥平面CB1D1 (B)AC1⊥BD(C)AC1⊥平面CB1D1 (D)异面直线AD 与CB 所成的角为60°15（2007四川文）如图，l1、l2、l3是同一平面内的三条平行直线，l1与l2与l3间的距离是2，正三角形ABC 的三顶点分别在l1、l2、l3上，则△ABC 的边长是（ D ）A.23B.364 C. 473-D.3212-16.（2007四川理）如图，l1、l2、l3是同一平面内的三条平行直线，l1与l2间的距离是1， l2与l3间的距离是2，正三角形ABC 的三顶点分别在l1、l2、l3上，则△ABC 的边长是（ D ）（A ）32（B ）364（C ）4173（D ）321217.（2007天津文、理）设a b ，为两条直线，αβ，为两个平面，下列四个命题中，正确的命题是（ D ）A ．若a b ，与α所成的角相等，则a b ∥B ．若a α∥，b β∥，αβ∥，则a b ∥C ．若a α⊂，b β⊂，a b ∥，则αβ∥D ．若a α⊥，b β⊥，αβ⊥，则a b ⊥18.（2007浙江文、理）若P 是两条异面直线l 、m 外的任意一点，则（ B ）(A)过点P 有且仅有一条直线与l 、m 都平行 (B)过点P 有且仅有一条直线与l 、m 都垂直 (C)过点P 有且仅有一条直线与l 、m 都相交 (D)过点P 有且仅有一条直线与l 、m 都异面19.（2007福建理)顶点在同一球面上的正四棱柱ABCD －A ’B ’C ’D ’中，AB ＝1，AA’＝，则A 、C 两点间的球面距离为（ B ）AB CD正视图侧视图俯视图20.(2007重庆文)垂直于同一平面的两条直线（ A ） （A ）平行 （B ）垂直 （C ）相交 （D ）异面21.（2007重庆理）若三个平面两两相交，且三条交线互相平行，则这三个平面把空间分成（ C ）A ．5部分 B.6部分 C.7部分 D.8部分22.(2007海南、宁夏文、理)已知某个几何体的三视图如下， 根据图中标出的尺寸（单位：cm ），可得这个几何体的体积是（ B ）Ａ．34000cm 3Ｂ．38000cm 3Ｃ．32000cmＤ．34000cm23．(2007海南、宁夏文)已知三棱锥S ABC -的各顶点都在一个半径为r 的球面上，球心O 在AB 上，SO ⊥底面ABC ，AC =，则球的体积与三棱锥体积之比是（ D ）Ａ．π Ｂ．2π Ｃ．3π Ｄ．4π24．(2007海南、宁夏理)一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱，这个四棱锥的底面为正方形，且底面边长与各侧棱长相等，这个三棱锥的底面边长与各侧棱长也都相等．设四棱锥、三棱锥、三棱柱的高分别为1h ，2h ，h ，则12::h h h =（ B ）2:2 2 2: 25．（2007江西文）四面体ABCD 的外接球球心在CD 上，且CD ＝2，AB ＝3，在外接球面上两点A 、B 间的球面距离是（Ｃ ）A ．6π B ．3π C ．32π D ．65π26．（2007江西理）如图，正方体AC1的棱长为1，过点A 作平面A1BD 的垂线，垂足为点H ．则以下命题中，错误的命题是（ D ） A ．点H 是△A1BD 的垂心 B ．AH 垂直平面CB1D1C ．AH 的延长线经过点C1D ．直线AH 和BB1所成角为45° 27. （2007全国Ⅰ文、理）如图，正四棱柱ABCD-A1B1C1D1中，AA1=2AB ， 则异面直线A1B 与AD1所成角的余弦值为（ Ｄ ）（A ）51（B ）52 （C ）53 （D ）5428（2007全国Ⅱ理）已知正三棱柱ABC-A1B1C1的侧棱长与底面边长相等，则AB1与侧面ACC1A1所成角的正弦等于（ A ） (A)46 (B) 410 (C) 22(D) 2329.（2007全国Ⅱ文）已知正三棱锥的侧棱长为底面边长的2倍，则侧棱与底面所成角的余弦值等于（ A ）(A)63(B)43(C)22(D)23 30．（2007山东文、理）下列几何体各自的三视图中，有且仅有两个视图相同的是（ D ）A ．①②B ．①③C ．①④D ．②④31（2007陕西文）Rt △ABC 的三个顶点在半径为13的球面上，两直角边的长分别为6和8，则球心到平面ABC 的距离是（ Ｄ ）（A ）5 （B ）6 （C ）10 （D ）1232.（2007陕西理）一个正三棱锥的四个顶点都在半径为1的球面上，其中底面的三个顶点在该球的一个大圆上，则该正三棱锥的体积是（ Ｂ ）（A ）433(B)33 (C)43 (D)12333.（2007四川文、理）设球O 的半径是1，A 、B 、C 是球面上三点，已知A 到B 、C 两点的球面距离都是2π，且二面角B-OA-C 的大小是3π，则从A 点沿球面经B 、C 两点再回到A 点的最短距离是（ C ）(A)67π (B)45π (C)34π(D)23π二、填空题： 1．（2007江西文）如图，正方体AC1的棱长为1，过点A 作平面A1BD 的垂线，垂足为点H ．则以下命题中，错误的命题是A ．点H 是△A1BD 的垂心B ．AH 垂直平面CB1D1C ．二面角C —B1D1—C1的正切值为2D ．点H 到平面A1B1C1D1的距离为43其中真命题的代号是 A ，B ，C ．(写出所有真命题的代号)2.（2007上海理）在平面上，两条直线的位置关系有相交、平行、重合三种． 已知αβ，是两个 相交平面，空间两条直线12l l ，在α上的射影是直线12s s ，，12l l ，在β上的射影是直线12t t ，．用1s 与2s ，1t 与2t 的位置关系，写出一个总能确定1l 与2l 是异 面直线的充分条件： 21//s s ，并且1t 与2t 相交（//1t 2t ，并且1s 与2s 相交） ．3.（2007浙江文、理）已知点O 在二面角α－AB －β的棱上，点P 在α内，且∠POB ＝45°．若对于β内异于0的任意一点Q ，都有∠POQ ≥45°，则二面角α－AB －β的大小是__900__．4.(2007安徽理)在正方体上任意选择4个顶点，它们可能是如下各种几何形体的4个顶点，这些几何形体是 ①③④⑤ （写出所有正确结论的编号）.①矩形；②不是矩形的平行四边形；③有三个面为等腰直角三角形，有一个面为等边三角形的四面体；④每个面都是等边三角形的四面体； ⑤每个面都是直角三角形的四面体.5.（2007湖南文）棱长为1的正方形1111ABCD A B C D -的8个顶点都在球O 的表面上，则球O 的表面积是 3π ；设E 、F 分别是该正方形的棱11AA 、DD 的中点，则直线EF 被球O 截得的线段长为 .1C C B 1B 1A A 6．（2007江苏）正三棱锥P ABC -高为2，侧棱与底面所成角为45，则点A 到侧面PBC 的距离是.7．（2007辽宁文、的正六棱柱的所有顶点都在一个球的面上，则此球的体积为 π34 ．8.（2007全国Ⅰ文）正四棱锥S-ABCD 的底面边长和各测棱长都为2，点S 、A 、B 、C 、D 都在同一个球面上，则该球的体积为4π39.（2007全国Ⅰ理）一个等腰直角三角形的三个顶点分别在正三棱柱的三条侧棱上.已知正三棱柱的底面边长为2,则该三角形的斜边长为10.（2007全国Ⅱ文、理）一个正四棱柱的各个顶点在一个直径为2cm 的球面上。

年高考数学试题汇编 立体几何一、选择题1．（全国Ⅰ•理•7题）如图，正四棱柱1111D C B A ABCD -中，AB AA 21=，则异面直线11AD B A 与所成角的余弦值为（ D ）A ．51 B ．52 C ．53 D ．542．（全国Ⅱ•理•7题）已知正三棱柱ABC －A 1B 1C 1的侧棱长与底面边长相等，则AB 1与侧面ACC 1A 1所成角的正弦等于（ A ）A ．64B ．104C ．22D ．323．（北京•理•3题）平面α∥平面β的一个充分条件是（ D ）A ．存在一条直线a a ααβ，∥，∥B ．存在一条直线a a a αβ⊂，，∥C ．存在两条平行直线a b a b a b αββα⊂⊂，，，，∥，∥D ．存在两条异面直线a b a a b αβα⊂，，，∥，∥4．（安徽•理•2题）设l ，m ，n 均为直线，其中m ，n 在平面α内，“l α⊥”是l m ⊥且“l n ⊥”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件5．（安徽•理•8题）半径为1的球面上的四点D C B A ,,,是正四面体的顶点，则A 与B 两点间的球面距离为（ ）A ．)33arccos(-B ．)36arccos(-C ．)31arccos(-D ．)41arccos(-6．（福建•理•8题）已知m ，n 为两条不同的直线，α，β为两个不同的平面，则下列命题中正确的是（ D ）A ．,,//,////m n m n ααββαβ⊂⊂⇒B ． //,,//m n m n αβαβ⊂⊂⇒C ．,//m m n n αα⊥⊥⇒D ． //,m n n m αα⊥⇒⊥．（福建•理•10题）顶点在同一球面上的正四棱柱ABCD －A 1B 1C 1D 1中，AB ＝1，AA 1＝，则A 、C 两点间的球面距离为（ B ）A ．4πB ．2πC ．24π D ．22π8．（湖北•理•4题）平面α外有两条直线m 和n ，如果m 和n 在平面α内的射影分别是1m 和1n ，给出下列四个命题：①1m ⊥1n ⇒m ⊥n ； ②m ⊥n ⇒1m ⊥1n ；③1m 与1n 相交⇒m 与n 相交或重合； ④1m 与1n 平行⇒m 与n 平行或重合； 其中不正确的命题个数是（ D ）A.1B.2C.3D.4 9．（湖南•理•8题）棱长为1的正方体1111ABC D A B C D -的8个顶点都在球O 的表面上，E F ，分别是棱1A A ，1DD 的中点，则直线E F 被球O 截得的线段长为（ D ）A ．22B ．1C ．212+ D ．210．（江苏•理•4题）已知两条直线,m n ，两个平面,αβ，给出下面四个命题： ①//,m n m n αα⊥⇒⊥ ②//,,//m n m n αβαβ⊂⊂⇒ ③//,////m n m n αα⇒ ④//,//,m n m n αβαβ⊥⇒⊥ 其中正确命题的序号是（ C ）A ．①③B ．②④C ．①④D ．②③ 11．（江西•理•7题）如图，正方体AC 1的棱长为1，过点A 作平面A 1BD 的垂线，垂足为点H ．则以下命题中，错误．．的命题是（ D ） A ．点H 是△A 1BD 的垂心 B ．AH 垂直平面CB 1D 1C ．AH 的延长线经过点C 1D ．直线AH 和BB 1所成角为45° 12．（辽宁•理•7题）若m n ，是两条不同的直线，αβγ，，是三个不同的平面，则下列命题中的真命题是（ ）A ．若m βαβ⊂⊥，，则m α⊥B ．若m αγ= n βγ= ，m n ∥，则αβ∥C ．若m β⊥，m α∥，则αβ⊥D ．若αγ⊥，αβ⊥，则βγ⊥．（陕西•理•6题）一个正三棱锥的四个顶点都在半径为1的球面上，其中底面的三个顶点在该球的一个大圆上，则该正三棱锥的体积是（ B ）A ．433 B ．33 C ． 43 D ．12314．（四川•理•4题）如图，ABCD -A 1B 1C 1D 1为正方体，下面结论错误．．的是（ D ）A ．BD ∥平面CB 1D 1 B ．AC 1⊥BDC ．AC 1⊥平面CB 1D 1 D ．异面直线AD 与CB 1角为60°15．(宁夏•理•8题) 已知某个几何体的三视图如下，根据图中标出的尺寸（单位：cm ），可得这个几何体的体积是（ B ）Ａ．34000cm 3Ｂ．38000cm 3Ｃ．32000cmＤ．34000cm16．（四川•理•6题）设球O 的半径是1，A 、B 、C 是球面上三点，已知A 到B 、C 两点的球面距离都是2π，且三面角B -OA -C 的大小为3π，则从A 点沿球面经B 、C 两点再回到A 点的最短距离是（ C ）A ．67π B ．45π C ．34π D ．23π17．（天津•理•6题）设a b ，为两条直线，αβ，为两个平面，下列四个命题中，正确的命题是（ D ）Ａ．若a b ，与α所成的角相等，则a b ∥ Ｂ．若a b αβ，∥∥，αβ∥，则a b ∥Ｃ．若a b a b αβ⊂⊂，，∥，则αβ∥ Ｄ．若a b αβ⊥⊥，，αβ⊥，则a b ⊥18．（浙江•理•6题）若P 是两条异面直线,l m 外的任意一点，则（ B ）A ．过点P 有且仅有一条直线与,l m 都平行B ．过点P 有且仅有一条直线与,l m都垂直C ．过点P 有且仅有一条直线与,l m 都相交D ．过点P 有且仅有一条直线与,lm2020正视图20侧视图101020俯视图二、填空题19．（全国Ⅰ•理•16题）一个等腰直角三角形的三个顶点分别在正三棱柱的三条侧棱上。