下载文档原格式
第四章屈服准则在社会生活中，人们不可避免地会面临各种各样的压力和挑战。
在一些情况下，为了达到个人的目标或解决问题，我们可能需要考虑屈服准则。
屈服准则是指在面对一定的压力或影响力时，个体为了适应环境或达到特定目标而改变自己的原则、价值观或行为。
屈服准则是一个复杂的社会心理现象，其背后涉及到多种因素。
首先，人们在社会中生活，需要与不同的人打交道。
在这个过程中，我们会受到他人的意见、期望和群体压力的影响。
有时为了维护人际关系，我们可能会妥协自己的立场，进行屈服。
其次，人们不同的心理需求也会影响屈服准则的运用。
例如，对于那些追求社会认同感、归属感的人来说，他们可能更容易受到群体的影响。
在追求个人目标的过程中，他们可能会为了得到认同和接纳而改变自己的行为。
此外，文化差异也会影响屈服准则的运用。
在一些个人主义的社会中，人们更强调个体的自由和独立，可能不太愿意屈服于他人的压力。
相反，在一些集体主义的社会中，人们更注重团队合作和社会阶层秩序，更容易受到群体的影响。
屈服准则的运用不仅仅是单向的，也可以是双向的。
即使在屈服的过程中，个体也可以对外界施加影响。
当个体在一个强势群体中时，可能会改变自身的态度和行为，以适应群体的期望。
然而，同时也可能通过自己的言行来影响群体，使得群体在其中一种程度上屈服于个体的意愿。
在一些情况下，个体的屈服可能会带来一些负面的后果。
例如，在政治环境中，个体可能会因为政府的压力而放弃自己的信仰或原则，甚至违背良心。
在家庭中，父母可能因为对子女的过度要求而导致孩子过度消沉或逆反。
然而，在一些情况下，屈服准则也可以起到积极的作用。
在一些争议问题上，个体通过屈服可以促成双方的妥协和和解，达到社会和谐。
在团队合作中，个体也可能会为了整体利益而妥协自己的意见，以达成共同的目标。
为了更好地应对屈服准则，个体需要保持对自己的价值观和原则的清晰认知，有自己的立场和底线。
同时，也需要了解他人的需求和期望，做到灵活适应。
第四章 屈服准则第一节 真实应力应变曲线单向拉伸（或压缩）→屈服应力 sσ继续变形→材料强化→流动应力（真实应力） 真实应力应变曲线可以由实验建立一 拉伸试验曲线单向拉伸：2323211,0,εεεσσσ-====存在等效应力1σσ= 1εε=， 因此εσεσ-⇒-曲线一致（一）拉伸图和条件应力——应变曲线 00A F=σ 0ιιε∆=p.比例极限 e.弹性极限 c.屈服极限 b.抗拉强度（颈缩点）b s σσσ,2.0,概念与定义（二）真实应力——应变曲线真实应力()εσε+===10A FA F S ， 真实应变()ε+∈=1ln劲缩后断裂点：K K K A F S = K nK A A 0ι=∈修正：ρ811d KKS S +=（颈缩处为三向应力）（三）失稳点特性（S ：真实应力）()bbds S =AA n n SA F 00......ιιι=∈==∈=∴e A A 0因此∈=e A S F 0 由于失稳点F有极大值，dF=0()00=∈-⇒∈-d se d e A ts化简得dS-Sd ∈=0或 b S d dS=∈即：失稳点处曲线的斜率等于纵坐标值二 压缩试验曲线拉伸时∈达不到很大（一般∈≤1.0），但压缩时存在摩擦必须解决方法：1） 直接消除摩擦的圆柱体压缩法 2） 外推法拉伸曲线与压缩曲线略有区别（压缩时S 略大）三 真实应力—应变曲线的简化形式目的：便于计算 硬化曲线图1） 指数型()幂次式硬化n B S ∈= ()失稳点b n =∈且0<n<1)(1b B S ms ∈+=σ(有初始值硬化)2）直线型()()2sb S s Dc D S σσ-=∈+=直线硬化，用于室温下大变形s S σ=(无加工硬化)用于高温低速变形，理想弹塑性。
∈E =S c ∈≤∈()c s D S ∈-∈+=1σ c ∈≥∈弹塑性线性硬化，用于室温下小变形第二节 理想塑性材料的屈服准则一 定义及有关概念单向应力时：只要单向应力达到屈服极限，材料就屈服，进入塑性状态。
一．屈服准则的概念1 ．屈服准则A.受力物体内质点处于单向应力状态时，只要单向应力大到材料的屈服点时，则该质点开始由弹性状态进入塑性状态，即处于屈服。
B.受力物体内质点处于多向应力状态时，必须同时考虑所有的应力分量。
在一定的变形条件（变形温度、变形速度等）下，只有当各应力分量之间符合一定关系时，质点才开始进入塑性状态，这种关系称为屈服准则，也称塑性条件。
它是描述受力物体中不同应力状态下的质点进入塑性状态并使塑性变形继续进行所必须遵守的力学条件，这种力学条件一般可表示为f（σij）＝C又称为屈服函数，式中C是与材料性质有关而与应力状态无关的常数，可通过试验求得。
屈服准则是求解塑性成形问题必要的补充方程。
2 ．有关材料性质的一些基本概念A.理想弹性材料物体发生弹性变形时，应力与应变完全成线性关系，并可假定它从弹性变形过渡到塑性变形是突然的。
B.理想塑性材料（又称全塑性材料）材料发生塑性变形时不产生硬化的材料，这种材料在进入塑性状态之后，应力不再增加，也即在中性载荷时即可连续产生塑性变形。
C.弹塑性材料在研究材料塑性变形时，需要考虑塑性变形之前的弹性变形的材料这里可分两种情况：Ⅰ.理想弹塑性材料在塑性变形时，需要考虑塑性变形之前的弹性变形，而不考虑硬化的材料，也即材料进入塑性状态后，应力不再增加可连续产生塑性变形。
Ⅱ.弹塑性硬化材料在塑性变形时，既要考虑塑性变形之前的弹性变形，又要考虑加工硬化的材料，这种材料在进入塑性状态后，如应力保持不变，则不能进一步变形。
只有在应力不断增加，也即在加载条件下才能连续产生塑性变形。
D.刚塑性材料在研究塑性变形时不考虑塑性变形之前的弹性变形。
这又可分两种情况：Ⅰ.理想刚塑性材料在研究塑性变形时，既不考虑弹性变形，又不考虑变形过程中的加工硬化的材料。
Ⅱ.刚塑性硬化材料在研究塑性变形时，不考虑塑性变形之前的弹性变形，但需要考虑变形过程中的加工硬化材料。
真实应力-应变曲线及某些简化形式二．屈雷斯加（ H.Tresca ）屈服准则当受力物体（质点）中的最大切应力达到某一定值时，该物体就发生屈服。
屈服准则、失效准则、硬化准则、速率0)为什么讨论这些基本问题有限元技术发展到今天，其算法基本上已经成熟。
对从事有限元软件开发的⼈员⽽⾔，主要的⼯作就是根据新材料的发展不断补充各种材料模型，不断完善材料库，同时也不断完善单元库；⽽对有限元使⽤⼈员来说，主要的⼯作就是建⽴⼏何模型，选择合适的材料及单元，设置求解参数。
选择单元及设置求解参数主要牵涉到有限元基本算法，通过集中的学习可以较快的掌握；⽽材料模型种类繁杂，有时候并不容易选择，有必要群策群⼒，共同学习。
我先抛砖引⽟，真诚希望⼤家能把这些⼯作做起来。
为容易理解计，尽量避免使⽤特别专业的词汇。
(1)屈服对许多延展性较好的材料（如⼤多数⾦属）⽽⾔，其弹性和⾮弹性⾏为⼀般⽤屈服强度（yield strength)这个标量来区分、界定。
在ANSYS⾥，屈服点（yield point)和⽐例极限(proportional limit)被假定为是⼀致的。
应⼒分量的组合千变万化，不可能对每个应⼒状态都指定屈服强度，屈服准则的作⽤就是将林林总总的多向应⼒转化为单向应⼒（屈服强度⼀般通过单向拉伸试验来测定，因为这个实验最简单。
），然后将转化后的等效应⼒和屈服强度进⾏⽐较。
在ANSYS⾥，主要有von Mises 和 Hilll（可以通过TB,HILL指定Hill Potential)两类准则。
当然⼀些塑性模型有⾃⼰特殊的屈服准则，如Drucker-Prager 。
失效指材料失去承载能⼒或者不能满⾜规定的使⽤要求（如过⼤的变形等），对脆性材料，失效⼀般表现为断裂，对延展性材料，失效的表现形式可以是最后的断裂，或者是产⽣永久变形，或过⼤的变形等等。
ANSYS6.0以后，FC系列命令可以⽤来为所有的单元指定失效准则，如最⼤主应⼒，最⼤主应变，蔡-吴准则等等，和TB,FAIL命令有些类似。
对复合材料单元（如SHELL91/99，SOLID46/191)也可以⽤TB,FAIL指定失效；对混凝⼟（SOLID65)，可以使⽤TB,CONCR指定裂纹的产⽣条件。
FASTAMP
专业钣金成形快速仿真软件FASTAMP 增量理论本构方程
FASTAMP 专业钣金成形快速仿真软件FASTAMP 专业钣金成形快速仿真软件
FASTAMP 专业钣金成形快速仿真软件全量形变理论本构方程
FASTAMP 专业钣金成形快速仿真软件
全量形变理论本构方程
⎦
⎣
090
FASTAMP 各向同性屈服准则
FASTAMP FASTAMP 专业钣金成形快速仿真软件FASTAMP 专业钣金成形快速仿真软件
FASTAMP 专业钣金成形快速仿真软件
材料的J2随动强化本构关系
K εσ=FASTAMP 专业钣金成形快速仿真软件
板料各向异性
FASTAMP 各向异性参数R 定义FASTAMP 各向异性系数ΔR
FASTAMP 专业钣金成形快速仿真软件FASTAMP 专业钣金成形快速仿真软件
FASTAMP 专业钣金成形快速仿真软件Barlat_Lian 屈服准则
FASTAMP 专业钣金成形快速仿真软件
Barlat 六参量正交各向异性屈服准则
6
FASTAMP 各种屈服准则比较
FASTAMP J2流动理论
FASTAMP 专业钣金成形快速仿真软件FASTAMP 专业钣金成形快速仿真软件
Barlat_Lian 屈服准则
FASTAMP 专业钣金成形快速仿真软件Barlat 六参量正交各向异性屈服准则
FASTAMP 专业钣金成形快速仿真软件。
第四章 屈服准则§ 4-1屈服准则的意义：屈服是弹性变形的终了，塑性变形的开始。
屈服点是一个方向性的从量变到质变的转折点，屈服点以下为弹性变形区，在该区域，随着应力增加，变形量也不断增加，应力和应变的量不断积累，如果积累的量不超过屈服点，一旦卸载，应力和变形又回到原处。
如果积累的量超过了屈服点，材料性质则发生了质的变化，卸载之后，应力和变形都不会回到原处。
材料内部有残余应力，也有不可回复的塑性变形。
屈服点是材料性能上的一个转折点或者说分界点。
屈服点以下的变形特点是线性、单值、可逆，屈服点以上的变形特点恰恰相反，非线性、非单值、不可逆。
因此，屈服点以下是弹性力学研究的范围，而屈服点以上是塑性力学研究的范围。
从弹性方面说，它是弹性变形的极限，是强度的最高峰，由此构成了强度理论，从事结构研究的人绝对不能接近这一值，他们的活动范围是小于该值。
从塑性加工讲，屈服仅仅是塑性变形的开始，一切塑性加工必须从这一点开始，由此构成了屈服准则。
因此可以说，强度理论和屈服准则是同一事物的两个不同的侧面，必须联系起来看，质点处于单向应力状态下，若s σσ=1，对于结构而言，构件已经失效。
对于塑性加工，例如拔丝加工刚刚开始。
我们已 经学过第三][31σσσ≤-、第四强度理论])()()[(21213232221σσσσσσ-+-+-0≤，将第三、第四强度理论综合起来，可以写成C f ij ≤)(σ；和这两个理论相对应的屈服准则可以写成C f ij =)(σ，由此可见，屈服准则可以定义为：当各应力分量之间符合一定关系时，质点才进入塑性状态。
因为它是在解塑性力学问题时，除力学、几何、物理方程之外的补充方程，故又称塑性方程。
屈服准则是各应力分量之间的一种组合关系，这种关系是无限的，所发不能用有限的实验去穷属它，而只能在理想化的理论分析的基础上，用有限的实验支验证它，在逻辑学上叫有限归纳，所以，到目前为止，屈服准则的本质仍然是分析（推理）型的。
实验验证仍在进行，或许到了某一限度会有突破。
§ 4-2 有关材料性质的一些基本概念一 连续：材料中没有空隙、裂纹。
二 均质：各质点性能一样。
三 各向异性：材料在各个方向上的性能不一样。
四 各向同性：材料在各个方向上的性能一样。
五 理想弹性材料：弹性变形时应力应变关系成线性的材料。
六 理想塑性材料：塑性变形时不产生硬化的材料。
进入塑性状态后应力不再增加可连续产生塑性变形。
七 变形硬化材料：塑性变形时产生硬化的材料，进入塑性状态后不断增加应力才可连续产生塑性变形。
八 刚塑性材料：在塑 性变形前象刚体一样不产生弹性变形，而到达屈服点后不再增加可连续产生塑性变形。
§ 4-3 屈雷斯加（Tresca ）准则一 定义：材料质点中的最大剪应力达到某一定值时材料产生屈服。
二 数学表达式：c =-21σσ ； c =-31σσ； c =-32σσ；当已知1σ、2σ、3σ的值，且有321σσσ≥≥时，则屈雷斯加（Tresca ）准则可写成c =-31σσ；更为简单。
从莫尔圆方面讲，莫尔圆的最大直径达到一定值时材料屈服。
三 屈雷斯加（Tresca ）准则的优缺点：1 优点：一阶线性，数学上处理非常方便，尤其是已知1σ、2σ、3σ的值时，且有321σσσ≥≥时，则屈雷斯加（Tresca ）准则可写成c =-31σσ。
2 缺点：该准则不考虑2σ，在理论上不完整，如果1σ、2σ、3σ的值未知是，不能确定321σσσ≥≥时，数学上处理不一定方便。
四 常数C 的确定：屈服准则应该适用于任何应力状态的组合：故可用简单的材料试验测定常数C 。
1 单向应力状态：单向拉伸则有0;321===σσσσs ; 则s c σσσ==-31。
2 纯剪应力状态：k k-===3210σσσs k c σσσ===-231; s k σ21=这是一个很重要的结论，C 只与材料有关，只与变形历史有关。
这一准则是法国人Tresca1864年研究土力学时，通过对挤压的研究提出的。
§ 4-4 密席斯屈服准则(Mises)一 定义：当材料质点的应力状态的等效应力达到一定值时，材料就会屈服。
二 数学表达式：C =-+-+-=])()()[(21213232221σσσσσσσ三 优缺点：1 优点：全面考虑了三个分量1σ、2σ、3σ，并且从应力到能量在数学上比较严谨。
2 缺点：二阶非线性，数学上处理比较复杂。
四 常数C 的确定： 1单向应力状态：有0;321===σσσσs ;s C σσσσσσσσσ===-+-+-=1213232221])()()[(21；s C σ=∴2 纯剪应力状态：;;0;321k k -===σσσs C k k k k σ==--+++-])()0()0[(21222;s C k σ==∴3; k=s s σσ577.031=k s3])()()[(21213232221==-+-+-=σσσσσσσσ五 物理意义：1924年Henky 阐明了Mises 准则的物理意义，这就是当材料的质点内的单位体积上的变形能达到某临界值时，材料屈服。
Nadai 则认为，Mises 准则的意义是八面体面上的剪应力达到一定值时，材料就屈服。
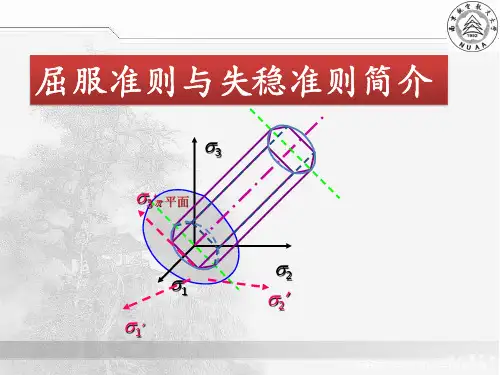
即：s στ328=§ 4-5 屈服准则的几何表达---屈服表面和屈服轨迹 一 应力空间的屈服表面： 1 应力空间：1） 定义：以三条主应力为坐标轴构成的空间叫应力空间。
2） 应力空间的点与变形体内质点的应力状态一一对应。
变形体内任意点的应力状态为()321σσσ，按此值可以在应力空间中确定一个点p ，p 点的坐标为()321σσσ，反之，在应力空间中有一点，就可以确定一个应力状态，因此，应力状态与应力空间中的点是一一对应的。
2 应力空间中的应力球张量：1） 等倾线的定义：与每一个坐标男的夹角都相等 直线叫等倾线。
2） 应力空意味等倾线的意义：等倾线上的每一点都代表一个球张量。
在应力空间第一卦限中作等倾线ON ，在ON 线上任取一点M ，M 点的坐标分别为()321m m m σσσ，它们在三条坐标轴上的投影为：ασcos 1OM m =; βσcos 2OM m =;γσcos 3OM m =; 因为在等倾线上γβα==；所以有： 321m m m σσσ==；M 点表示一个球应力状态，是一个应力球张量。
由于M 点的任意性，可以确定ON 轴上的每一点都是一个球张量。
3 在应力空间中应力偏张量的表示：在应力空间中，任意点p 代表着一个点和应力状态，坐标为()321σσσ，矢量p o同样代表这点的应力状态，将p o向ON 投影得OM ，则OM 等于OP 各分量在ON 上的投影之和，即OM =++γσβσασcos cos cos 321 1c o s c o s c o s 222=++γβα ; 又γβα== ; 31cos cos cos ===γβα；OM =++)(31321σσσ；又232221σσσ++=op ;=-=22OM op MP 23212232221)(31)(σσσσσσ++-++；展开合并同类项而后配方得：=MP σσσσσσσ32])()()[(31213232221=-+-+-p o代表一点的应力张量，M O 代表点的应力球张量，M O p o P M -=代表该点的应力偏张量。
在应力空间中，=MP 32σ=32s σ时材料就会屈服。
4 应力空间中的屈服准则轨迹： 1） Mises 屈服轨迹：过p 点作垂直于ON 的平面，由O 点到平面上所有的点的矢量向ON 投影都为OM ，以M 为圆心，以MP 为半径，作圆，圆上的每一个点到M 的距离都等于MP ，圆上所有点所代表的应力状态的偏张量的模都为MP =32s σ，所以圆上的点表示屈服应力状态。
过p 点作ON 的平行线PQ ，以PQ 为母线作圆柱面，则该圆柱面上的每一点ON 的距离都等于MP ，以O 点到圆柱面上各点的矢量所代表的应力张量的偏张量的模均为MP =32s σ；所以柱面上每一点都代表屈服应状态。
在圆柱面内部的点所表示的应力张量的偏张量的模都小于MP =32s σ，都表示弹性应力状态。
对于刚塑性材料，s σσ=而不能大于s σ。
因为无更大的反作用力，点不会跑到圆柱而的外面。
2）Tresca 屈服准则轨迹：Tresca 屈服准则的数学表达式为：s σσσ=-21 ； s σσσ=-31； s σσσ=-32； ① s σσσ=-21; s σσσ±=-21 ;首先讨论s σσσ+=-21 当01=σ时，s σσ-=2; 得点（0，-s σ）；当02=σ时；s σσ=1；是点（s σ，0）； 所以，s σσσ+=-21是一条过点（0，-s σ）和点（s σ，0）的直线。
在空间是过点（s σ，0，0）、点（0，-s σ，0）的一个平面。
② s σσσ-=-21当01=σ时，s σσ=2; 得点（0，s σ）；当02=σ时；s σσ-=1；是点（-s σ，0）； 所以，s σσσ-=-21是一条过点（0，s σ）和点（-s σ，0）的直线。
在空间是过点（-s σ，0，0）、点（0，s σ，0）的一个平面。
③ s σσσ=-21平面的特性：211121)()(σσσσσσσσ-=---='-'m m ; 由此可见s σσσ=-21与应力球张量无关。
所以s σσσ±=-21两平面与ON 轴无交点，平行于ON 轴。
所以s σσσ±=-21在空间分别是过点（-s σ，0，0）、点（0，s σ，0）和过点（-s σ，0，0）、点（0，s σ，0）而且都平行于ON 轴的两平面。
同理可证s σσσ=-31在空间是过点（s σ，0，0）、点（0，0，-s σ）的一个平面和过点（-s σ，0，0）、点（0，0，s σ）的一个平面。
而s σσσ=-32，在空间是过点（0，-s σ，0）、点（0，0，s σ）的一个平面和过点（0，s σ，0）、点（0，0，-s σ）的一个平面。
这些平面都平等于ON 轴；且两相交，形成一个以ON 为轴的正六棱柱面。
3）Mises 准则和Tresca 准则的关系：在应力空间中，令点（s σ，0，0）为A 点，向量OA 的模为s σ，向ON 轴投影为OM s s ==σασ31cos ;OM s =σ31是A 点应力状态的应力球张量，A 点的应力偏张量应力为=-2231s s σσ32s σ，即过A 点的棱与ON 轴之的距离为32s σ。
并且棱与ON 轴平行。
而Mises 圆柱面的母线与ON 轴的距离或圆柱面的半径为32s σ；所以棱和圆柱面必定重合，也就是说，棱在圆柱面上，同理其它棱也在圆柱面上。
