下载文档原格式
《MATLAB与控制系统仿真》实验报告一、实验目的本实验旨在通过MATLAB软件进行控制系统的仿真，并通过仿真结果分析控制系统的性能。
二、实验器材1.计算机2.MATLAB软件三、实验内容1.搭建控制系统模型在MATLAB软件中，通过使用控制系统工具箱，我们可以搭建不同类型的控制系统模型。
本实验中我们选择了一个简单的比例控制系统模型。
2.设定输入信号我们需要为控制系统提供输入信号进行仿真。
在MATLAB中，我们可以使用信号工具箱来产生不同类型的信号。
本实验中，我们选择了一个阶跃信号作为输入信号。
3.运行仿真通过设置模型参数、输入信号以及仿真时间等相关参数后，我们可以运行仿真。
MATLAB会根据系统模型和输入信号产生输出信号，并显示在仿真界面上。
4.分析控制系统性能根据仿真结果，我们可以对控制系统的性能进行分析。
常见的性能指标包括系统的稳态误差、超调量、响应时间等。
四、实验步骤1. 打开MATLAB软件，并在命令窗口中输入“controlSystemDesigner”命令，打开控制系统工具箱。
2.在控制系统工具箱中选择比例控制器模型，并设置相应的增益参数。
3.在信号工具箱中选择阶跃信号，并设置相应的幅值和起始时间。
4.在仿真界面中设置仿真时间，并点击运行按钮，开始仿真。
5.根据仿真结果，分析控制系统的性能指标，并记录下相应的数值，并根据数值进行分析和讨论。
五、实验结果与分析根据运行仿真获得的结果，我们可以得到控制系统的输出信号曲线。
通过观察输出信号的稳态值、超调量、响应时间等性能指标，我们可以对控制系统的性能进行分析和评价。
六、实验总结通过本次实验，我们学习了如何使用MATLAB软件进行控制系统仿真，并提取控制系统的性能指标。
通过实验，我们可以更加直观地理解控制系统的工作原理，为控制系统设计和分析提供了重要的工具和思路。
七、实验心得通过本次实验，我深刻理解了控制系统仿真的重要性和必要性。
MATLAB软件提供了强大的仿真工具和功能，能够帮助我们更好地理解和分析控制系统的性能。
控制系统仿真答案一．选择题二．名词解释及简答题1．系统的三个属性是什么？请解释其具体含义。
答：系统的三个属性：整体性、相关性、隶属性。
整体性：各部分(子系统)不能随意分割。
相关性：各部分(子系统) 以一定的规律或方式相联系，由此决定了其特有的性能。
隶属性：不能清楚的分出系统“内部”与“外部”，常常需要根据研究的问题来确定哪些属于系统的内部因素，哪些属于外部环境，其界限也是随不同的研究目的而变化，将这一特性称之为隶属性。
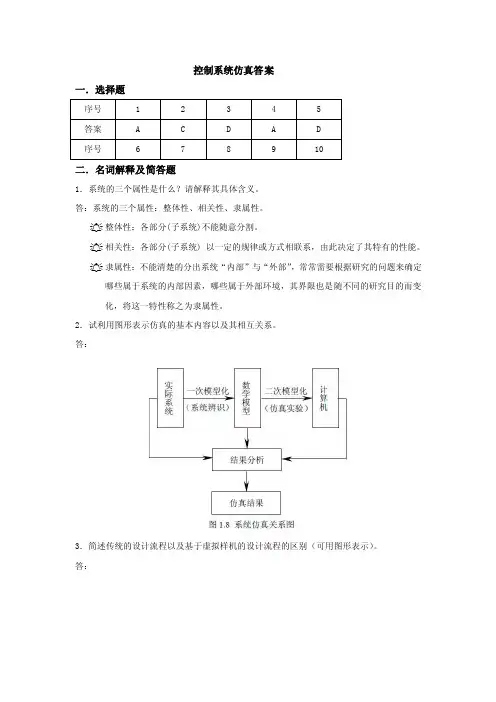
2．试利用图形表示仿真的基本内容以及其相互关系。
答：3．简述传统的设计流程以及基于虚拟样机的设计流程的区别（可用图形表示）。
答：三．判断题，正确的在括号内打“√”，错误的打“╳”，并改正错误结论重新阐述。
1．（√）为了限制所研究问题涉及的范围，一般用系统边界把被研究的系统与系统环境区分开来。
2．（╳）模型按数学模型的形式分为：物理仿真、数学仿真、数学－物理混合仿真或半实物仿真。
改1：按模型的性质分为：物理仿真、数学仿真、数学－物理混合仿真或半实物仿真。
改2：按数学模型的形式分为：连续系统仿真、离散事件系统仿真、离散—连续系统仿真。
3．（√）series函数可以将两个系统按串联方式连接，它即适合于连续时间系统，也适合于离散时间系统。
4．（√）S-函数为Simulink的“系统”函数，它是能够响应Simulink求解器命令的函数，采用非图形化的方法实现一个动态系统。
5．（╳）Matlab在执行运算符的优先级的时候，逻辑运算符“<”的优先级要高于矩阵乘法运算“*”的优先级。
改：Matlab在执行运算符的优先级的时候，逻辑运算符“<”的优先级要低于矩阵乘法运算“*”的优先级。
四、2、main(){float x,money;Scanf(“%f/n”,&x);If(x<50) then money=2.5*xElse if(x>=50 and x<100)Else if (x>=100)Then money=2.5*x*(1-0.2) ;Printf(“money=%f”,money);}五．综合题1．编程实现以下图形绘制。
一、实验目的1. 掌握控制系统仿真的基本原理和方法；2. 熟练运用MATLAB/Simulink软件进行控制系统建模与仿真；3. 分析控制系统性能，优化控制策略。
二、实验内容1. 建立控制系统模型2. 进行仿真实验3. 分析仿真结果4. 优化控制策略三、实验环境1. 操作系统：Windows 102. 软件环境：MATLAB R2020a、Simulink3. 硬件环境：个人电脑一台四、实验过程1. 建立控制系统模型以一个典型的PID控制系统为例，建立其Simulink模型。
首先，创建一个新的Simulink模型，然后添加以下模块：（1）输入模块：添加一个阶跃信号源，表示系统的输入信号；（2）被控对象：添加一个传递函数模块，表示系统的被控对象；（3）控制器：添加一个PID控制器模块，表示系统的控制器；（4）输出模块：添加一个示波器模块，用于观察系统的输出信号。
2. 进行仿真实验（1）设置仿真参数：在仿真参数设置对话框中，设置仿真时间、步长等参数；（2）运行仿真：点击“开始仿真”按钮，运行仿真实验；（3）观察仿真结果：在示波器模块中，观察系统的输出信号，分析系统性能。
3. 分析仿真结果根据仿真结果，分析以下内容：（1）系统稳定性：通过观察系统的输出信号，判断系统是否稳定；（2）响应速度：分析系统对输入信号的响应速度，评估系统的快速性；（3）超调量：分析系统超调量，评估系统的平稳性；（4）调节时间：分析系统调节时间，评估系统的动态性能。
4. 优化控制策略根据仿真结果，对PID控制器的参数进行调整，以优化系统性能。
调整方法如下：（1）调整比例系数Kp：增大Kp，提高系统的快速性，但可能导致超调量增大；（2）调整积分系数Ki：增大Ki，提高系统的平稳性，但可能导致调节时间延长；（3）调整微分系数Kd：增大Kd，提高系统的快速性，但可能导致系统稳定性下降。
五、实验结果与分析1. 系统稳定性：经过仿真实验，发现该PID控制系统在调整参数后，具有良好的稳定性。
控制系统仿真教学大纲控制系统仿真教学大纲控制系统仿真是现代工程领域中一项重要的技术手段，它通过构建数学模型和仿真环境，对实际控制系统进行模拟和分析。
作为一门综合性学科，控制系统仿真在工业自动化、航空航天、能源等领域都有广泛的应用。
为了培养学生的控制系统仿真能力，制定一份科学合理的教学大纲是非常必要的。
一、课程简介本课程主要介绍控制系统仿真的基本概念、原理和方法。
通过理论讲解和实践操作，使学生能够掌握仿真软件的使用技巧，了解仿真模型的建立过程，掌握仿真结果的分析与评估方法，培养学生的问题分析和解决能力。
二、教学目标1. 掌握控制系统仿真的基本概念和原理；2. 熟练使用常见的仿真软件，如MATLAB/Simulink；3. 能够建立控制系统的数学模型，并进行仿真实验；4. 能够分析仿真结果，评估系统性能，并提出改进方案；5. 培养学生的团队合作和创新思维能力。
三、教学内容1. 控制系统仿真概述a. 控制系统仿真的定义和意义b. 控制系统仿真的基本流程和方法c. 常见的仿真软件及其特点介绍2. 数学建模与仿真环境a. 控制系统的数学建模方法b. 仿真环境的选择与搭建c. 仿真模型的参数设置和输入输出分析3. 控制系统仿真实验a. PID控制器的仿真实验b. 系统辨识与模型预测控制的仿真实验c. 状态空间控制的仿真实验4. 仿真结果分析与评估a. 仿真结果的可视化分析方法b. 性能指标的计算与评估c. 仿真结果与实际系统的对比分析5. 仿真实验设计与报告撰写a. 仿真实验设计的基本原则和方法b. 仿真实验报告的撰写要点和格式规范四、教学方法1. 理论讲解：通过课堂讲解，让学生了解控制系统仿真的基本概念和原理。
2. 实验操作：通过实验操作，让学生亲自动手建立仿真模型，进行仿真实验。
3. 课堂讨论：通过课堂讨论，让学生分享仿真结果，互相学习和交流。
4. 课程设计：通过课程设计，让学生能够独立设计控制系统的仿真实验。
如何使用Matlab进行控制系统仿真概述控制系统在工程领域中扮演着重要角色，它用于控制和管理各种工程过程和设备。
而控制系统仿真则是设计、开发和测试控制系统的关键环节之一。
Matlab作为一种功能强大的工程计算软件，提供了丰富的工具和功能，可以帮助工程师进行控制系统仿真。
本文将简要介绍如何使用Matlab进行控制系统仿真，以及一些实用的技巧和建议。
1. Matlab的基础知识在开始控制系统仿真之前，有一些Matlab的基础知识是必要的。
首先，了解Matlab的基本语法和命令，熟悉Matlab的工作环境和编辑器。
其次，学会使用Matlab的集成开发环境（IDE）进行编程和数学建模。
熟悉Matlab的常用函数和工具箱，并了解如何在Matlab中导入和导出数据。
2. 定义系统模型在进行控制系统仿真之前，需要定义系统的数学模型。
根据具体情况选择合适的建模方法，如传递函数、状态空间或差分方程等。
在Matlab中，可以使用tf、ss 或zpk等函数来创建系统模型，并指定系统的参数和输入信号。
此外，Matlab还提供了Simulink这一强大的图形化建模环境，方便用户以图形化界面设计系统模型。
3. 设计控制器控制系统仿真的关键是设计合适的控制器，以实现所需的控制目标。
Matlab提供了各种控制器设计方法和工具，如PID控制器、根轨迹法、频域方法等。
用户可以使用Matlab的Control System Toolbox来设计和分析控制器，并在仿真中进行验证。
此外，Matlab还支持自适应控制和模糊控制等高级控制方法，可根据具体需求选择合适的方法。
4. 进行仿真实验在完成系统模型和控制器设计后，可以开始进行控制系统仿真实验。
首先，确定仿真实验的输入信号，如阶跃信号、正弦信号或随机信号等。
然后，使用Matlab中的sim函数将输入信号应用到系统模型中，并观察系统的输出响应。
通过调整控制器参数或设计不同的控制器，分析系统的性能和稳定性，并优化控制器的设计。
自动控制系统的建模与仿真自动控制系统的建模和仿真是实现控制系统设计、分析、调试和优化的一种重要方法。
本文将从控制系统建模的概念入手，介绍控制系统建模的基本方法，并通过实例介绍控制系统的仿真过程。
一、控制系统建模的基本概念1. 控制系统建模的概念控制系统建模是指将控制系统抽象为数学模型的过程，其目的是方便对控制系统进行设计、分析和优化。
2. 控制系统的分类根据输入输出信号的性质，控制系统可分为模拟控制系统和数字控制系统。
模拟控制系统是指输入输出信号为模拟信号的控制系统，数字控制系统是指输入输出信号为数字信号的控制系统。
3. 控制系统的基本结构控制系统由控制器、执行器和被控对象三部分组成。
控制器负责对被控对象进行信号处理和决策，输出控制信号；执行器接收控制信号，通过转换为相应的动力或能量信号控制被控对象的运动；被控对象是控制系统的实际操作对象，其状态受执行器控制信号影响而改变。
4. 控制系统的数学模型控制系统的数学模型是描述其输入输出关系的数学方程或模型，可将其简化为传递函数的形式。
控制系统的数学模型有两种主要表达方式，一种是状态空间表达式，一种是等效传递函数式。
二、控制系统建模的基本方法1. 确定控制系统类型和目标在建模之前，需要对控制系统的类型和目标进行确定，包括控制系统的输入和输出信号的特征、被控对象的特性等。
2. 建立被控对象的数学模型被控对象的数学模型包括其动态特性和静态特性。
动态特性即描述被控对象内部变化规律的数学模型，静态特性即描述被控对象输入输出关系的数学模型。
3. 建立控制器的数学模型控制器的数学模型要根据被控对象的数学模型和控制系统的控制目标进行设计。
4. 建立控制系统的数学模型将被控对象的数学模型和控制器的数学模型相结合，得到控制系统的数学模型，可推导得到控制系统的传递函数。
5. 对控制系统进行仿真通过仿真软件对控制系统进行仿真，可以实现在不同工作条件下模拟出控制系统的工作状态和性能，以验证控制系统的可行性。
控制系统仿真简介控制系统仿真是指通过使用计算机软件模拟和分析各种控制系统的工作原理和性能。
它可以帮助工程师们在设计和优化控制系统之前，预先评估系统的性能，并对其中可能存在的问题进行分析和改进。
控制系统仿真通常包含建模、仿真和分析三个主要阶段。
在建模阶段，工程师们将实际的控制系统抽象为数学模型，并将其转化为计算机可识别的形式。
在仿真阶段，利用计算机软件运行模型，模拟控制系统在不同输入和工作条件下的行为。
最后，在分析阶段，工程师们对仿真结果进行评估和分析，以便理解控制系统的性能并提出改进措施。
仿真平台常用的控制系统仿真平台包括MATLAB/Simulink、LabVIEW等。
MATLAB/Simulink是一个强大的数学计算和仿真环境，提供了丰富的工具箱和模型库，可用于建模和仿真各种控制系统。
LabVIEW是一种图形化编程环境，具有易于使用的界面和丰富的模块，使得控制系统仿真变得简单而高效。
这些仿真平台都提供了模型搭建、仿真运行和结果分析等功能。
工程师们可以通过使用这些平台，进行控制系统的整体仿真和性能评估。
建模在进行控制系统仿真之前，首先需要对实际系统进行建模。
建模是指将实际系统的物理过程抽象为数学方程或传递函数的形式，以便于计算机运算和仿真。
常用的建模方法包括物理建模和数据建模。
物理建模是基于实际系统的物理过程和原理，通过利用物理方程或控制方程来描述系统的动态行为。
数据建模则是通过对实际系统进行数据采集，建立数学模型来描述系统的行为。
在建模过程中，需要确定系统的输入、输出和状态变量，并根据系统的特性选择适当的数学模型。
常用的系统模型包括常微分方程模型、状态空间模型和传递函数模型等。
仿真运行建立完控制系统的数学模型后，就可以通过仿真运行来模拟系统的行为。
仿真运行是指利用计算机软件运行建立的模型，并通过对不同输入和工作条件的设定，观察系统的响应和输出结果。
在仿真运行中，可以通过指定系统的输入信号来模拟不同的工作情况。
控制系统仿真实验报告一、实验目的本次控制系统仿真实验的主要目的是通过使用仿真软件对控制系统进行建模、分析和设计，深入理解控制系统的工作原理和性能特点，掌握控制系统的分析和设计方法，提高解决实际控制问题的能力。
二、实验设备与软件1、计算机一台2、 MATLAB 仿真软件三、实验原理控制系统是由控制对象、控制器和反馈环节组成的一个闭环系统。
其工作原理是通过传感器测量控制对象的输出，将其与期望的输出进行比较，得到误差信号，控制器根据误差信号产生控制信号，驱动控制对象，使系统的输出逐渐接近期望的输出。
在仿真实验中，我们使用数学模型来描述控制对象和控制器的动态特性。
常见的数学模型包括传递函数、状态空间方程等。
通过对这些数学模型进行数值求解，可以得到系统的输出响应，从而对系统的性能进行分析和评估。
四、实验内容1、一阶系统的仿真建立一阶系统的数学模型，如一阶惯性环节。
使用 MATLAB 绘制系统的单位阶跃响应曲线，分析系统的响应时间和稳态误差。
2、二阶系统的仿真建立二阶系统的数学模型，如典型的二阶振荡环节。
改变系统的阻尼比和自然频率，观察系统的阶跃响应曲线，分析系统的稳定性、超调量和调节时间。
3、控制器的设计与仿真设计比例控制器（P 控制器）、比例积分控制器（PI 控制器）和比例积分微分控制器（PID 控制器）。
对给定的控制系统，分别使用不同的控制器进行仿真，比较系统的性能指标，如稳态误差、响应速度等。
4、复杂控制系统的仿真建立包含多个环节的复杂控制系统模型，如串级控制系统、前馈控制系统等。
分析系统在不同输入信号下的响应，评估系统的控制效果。
五、实验步骤1、打开 MATLAB 软件，新建脚本文件。
2、根据实验内容，定义系统的数学模型和参数。
3、使用 MATLAB 中的函数，如 step(）函数绘制系统的阶跃响应曲线。
4、对响应曲线进行分析，计算系统的性能指标，如超调量、调节时间、稳态误差等。
5、设计控制器，修改系统模型，重新进行仿真，比较系统性能的改善情况。
《控制系统计算机仿真—课程设计作业》姓名： 专业： 学号：1. 构造矩阵（1）试将.*A B 与B A *的结果相加，并找出相加后新矩阵中绝对值大于10的元素。
（2）组合成一个43的矩阵，第一列为按列顺序排列的A 矩阵元素，第二列为按列顺序排列的B 矩阵元素，第三列为按列顺序排列的C 矩 阵元素。
（1）matlab ： A=[-7 1;8 -3]; B=[4 2;5 7]; C=[5 9;6 2]; D=A.*B+A*Bnum=find(abs(D)>10); D(num)结果：D =-51 -5 57 -26 ans = -51 57 -26（2）matlab ：NEW=[A(1,:),A(2,:);B(1,:),B(2,:);C(1,:),C(2,:)]’ 结果：NEW =-7 4 5 1 2 9 8 5 6714259,,835762A B C -⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦-3 7 22. 绘制函数曲线，要求写出程序代码(1)在区间[0,2]π均匀的取50个点，构成向量X。
(2)在同一窗口绘制曲线y1=sin(2*t-0.3); y2=3cos(t+0.5)；要求y1曲线为红色点划线，标记点为圆圈；y2为蓝色虚线，标记点为星号。
程序代码:t=linspace(0,2*pi,50);y1=sin(2*t-0.3);y2=3*cos(t+0.5);plot(t,y1,'r.',t,y2,'b-');hold onplot(t,y1,'o',t,y2,'*');hold off3. 写出生成下图所示波形的MA TLAB 程序。
图中三个波形均为余弦波，x范围为[pi/2 ~7*pi/2] 。
要求它的正半波被置零；且在24[,]33ππ和810[,]33ππ处被削顶。
程序：x=linspace(pi/2,7*pi/2,100);y1=cos(x);figure（1）plot（x,y1）y1(find(y1>0))=0;figure(2)plot(x,y1)n=find((x>2*pi/3&x<4*pi/3)|(x>8*pi/3&x<10*pi/3));y1(n)=cos(2*pi/3);figure(3)plot(x,y1)4对于x=［－2π，2π］，y1=sinx、y2=cosx、y3=sin2x、y4=cos2x①用MATLAB语言分四个区域分别绘制的曲线，并且对图形标题及横纵坐标轴进行标注。
②另建一个窗口，不分区，用不同颜色、线型绘出四条曲线，并标注图例注解。
Matlab：x=linspace(-2*pi,2*pi,1000);y1=sin(x);y2=cos(x);y3=sin(2*x);y4=cos(2*x);figure(1)subplot(2,2,1)plot(x,y1)xlabel('ºá×ø±êx=[-2*pi,2*pi]');ylabel('×Ý×ø±êy=sin(x)')title('y=sin(x)ÔÚ[-2*pi,2*pi]Ö®¼äµÄÇúÏßͼ')subplot(2,2,2)plot(x,y2)xlabel('ºá×ø±êx=[-2*pi,2*pi]');ylabel('×Ý×ø±êy=cos(x)')title('y=cos(x)ÔÚ[-2*pi,2*pi]Ö®¼äµÄÇúÏßͼ')subplot(2,2,3);plot(x,y3);xlabel('ºá×ø±êx=[-2*pi,2*pi]');ylabel('×Ý×ø±êy=sin(2x)')title('y=sin(2x)ÔÚ[-2*pi,2*pi]Ö®¼äµÄÇúÏßͼ')subplot(2,2,4);plot(x,y4);xlabel('ºá×ø±êx=[-2*pi,2*pi]');ylabel('×Ý×ø±êy=cos(2x)')title('y=cos(2x)ÔÚ[-2*pi,2*pi]Ö®¼äµÄÇúÏßͼ')figure(2)plot(x,y1,'r-',x,y2,'b.',x,y3,'ko',x,y4,'g*')legend('y=sin(x)','y=cos(x)','y=sin(2x£©','y=cos(2x)')5. 请分析并修改下面的程序，使用矩阵或数组运算的顺序结构完成嵌套for语句的相同功能。
A=[1 2 3; 4 5 6; 7 8 9];[r c]=size(A);for i=1:1:rfor j=1:1:cif (A(i,j)>8 | A(i,j)<2)A(i,j)=0;endendend修改后的matlab：A=[1 2 3; 4 5 6; 7 8 9];A(find(A>8|A<2))=0;A6. 假设a 是这样一组数组：222()(1)(2)(3)a n a n a n a n =---+-，且(1)0,(2)1,(3)2a a a ===。
试分别用循环指令for 以及while 来寻求该数组中第一个大于10000 的元素。
Matlab ：a(1)=0;a(2)=1; a(3)=2; for i=4:infa(i)=a(i-1)^2-a(i-2)^2+a(i-3)^2; if a(i)>10000 break end end a(i),i 结果：ans =871431 i = 87. 编写分段函数⎪⎩⎪⎨⎧≤≤-<≤=其他021210)(x xx x x f 的函数文件，存放在文件ff.m 中，用input 语句输入x 值，计算)(),2()2-(∞f f f ，的值。
x=input('ÇëÊäÈëx=');if x>=0&x<1 f(x)=x; elseif x>=1&x<=2 f(x)=2-x; else f(x)=0; end f(x) 结果：请输入x=-2 f = 0 > ff.m请输入x=sqrt(2) f =0.5858 >> ff.m请输入x=inf f = 08. (2)将上题编程改为M 函数程序文件，该函数文件满足：对于任意输入的正整数n ，能够输出对应次数小球反弹的高度。
function ff=f(x)if nargin==0,x=1;end if x>=0&x<1 f(x)=x; elseif x>=1&x<=2 f(x)=2-x; elseif x<0disp('ÊäÈë´íÎó'); else f(x)=0; end f(x)9. 已知两个传递函数分别为：12212(),()313G x G x s s s==++①在MA TLAB 中分别用传递函数、零极点、和状态空间法表示； ②在MATLAB 中分别求出通过反馈、串联、并联后得到的系统模型；Matlab ：sys1=tf([1],[3 1]) ss(sys1) zpk(sys1)sys2=tf([2],[3,1,0]) ss(sys2) zpk(sys2)feedback(sys1,sys2,-1) parallel(sys1,sys2) series(sys1,sys2)10. 已知系统的方框图如图所示，试推导出从输入信号到输出信号的总系统模型。
Matlab ：sys1=tf([1],[1,1]);sys2=tf([1,0],[1,0,2]); sys3=tf([4,2],[1,2,1]);sys11=feedback(sys1*sys2,sys3,-1); sys4=tf([1],[1,0,0]); sys22=feedback(sys4,50,-1); sys5=tf([1,0,2],[1,0,0,14]); sys=3*feedback(sys11+sys22,sys5,-1)结果：Transfer function:6 s^8 + 15 s^7 + 168 s^6 + 417 s^5 + 384 s^4 + 2358 s^3 + 4662 s^2 + 2436 s + 84 -----------------------------------------------------------------------------------s^10 + 3 s^9 + 55 s^8 + 177 s^7 + 305 s^6 + 1382 s^5 + 2775 s^4 + 3882 s^3+ 7952 s^2 + 5716 s + 140411. 设单位负反馈控制系统的开环传递函数为：2()(717)KG s s s s =++（1）试绘制K=10,100时闭环系统的阶跃响应曲线，并计算上升时间，超调量和过渡时间； （2）绘制K=1000时闭环系统的阶跃响应曲线，与K=10，100所得的结果相比较，分析增益系数与系统稳定性的关系。
