第二章化学热力学基础

第二章化学热力学基础2.1 热力学概论2.1.11) 高炉炼铁反应Fe2O3 + 3CO = 2Fe + 3CO2 ?2) 汽车尾气污染问题2NO + 2CO = N2 + 2CO2 ？3) 将石墨转化为金刚石C (Graphite) = C (Diamond) ？实现这些化学反应的可能性及反应程度等问题需要化学热力学来解决热力学(themodynamics) ：不需要知道物质的内部结构，只从能量观点出发，专门研究能量相互转变过程中所遵循规律的科学。

热力学将宏观物体作为整体看待，直接以宏观实验与观察为基础，从物体表现出的整体宏观现象上总结抽象出共同的规律作为自然法则，然后进行逻辑推演，进而解释和解决各种有关问题。

其理论支柱是四条热力学基本定律，它们是在漫长的岁月中，总结大量正反两方面的实践经验抽象出的宏观法则。

✓热力学研究各种能量之间的转换关系，如电能和机械能、电能和热能等。

✓热力学研究在各种变化过程中发生的各种能量效应。

✓热力学能判断一定条件下的变化能否发生以及进行到什么程度。

所以，尽管热力学是物理学的分支学科，但其应用范围极其广泛，它可以应用于工程学、化学、生物学等学科。

本章从热力学应用于化学的角度，对热力学的基本原理给予初步简介，仅帮助同学们初步地了解如何从宏观角度解释一些化学问题的方法。

化学热力学利用热力学的基本方法、原理来研究化学变化和与化学变化有关的物理变化中能量的转化或传递的学科。

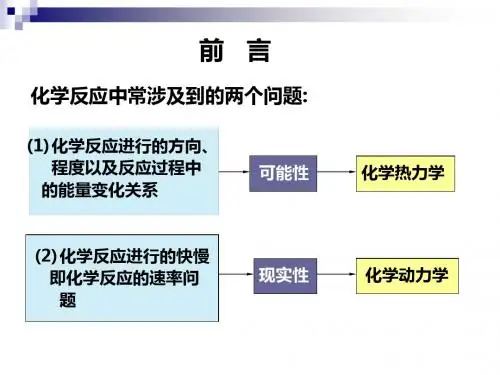
研究化学反应时，常遇到这样一些问题：当几种物质放在一起时，①它们能发生反应吗？②如果发生反应，能量如何变化？③反应是否可进行到底？④反应速率多大？⑤反应是如何进行的（反应机理）？化学热力学的研究范围:①②③属于化学热力学问题，也就是化学反应的方向、限度以及伴随的能量变化。

而④⑤属于化学动力学问题。

化学热力学的作用：☞预测反应发生的可能性及进行的方向（判据）（热力学第二定律）☞判断反应进行的限度（平衡问题）☞确定化学反应的热效应（热力学第一定律）化学热力学的局限性通过化学热力学的研究，能够比较满意地解决①②③这三个问题，但并不能够解决④⑤这两个问题，体现出化学热力学的局限性，因为：✓热力学的研究对象是宏观物体，对于个别原子、分子等微观粒子的性质是无能为力的。

第二章化学热力学基础学习重点一.理解并熟悉热力学有关的概念:体系和环境状态和状态函数过程和途径常见的三个体系:敞开、封闭、孤立体系常见的三个过程:等压、等容、等温过程热和功热力学能(内能)和焓变化学反应热,等容反应热、等压反应热生成焓和标准生成焓;键能和离解能,键能和反应热的关系熵和熵变,标准摩尔熵Gibbs自由能和Gibbs自由能变,标准摩尔生成Gibbs自由能二.理解并熟练运用几个定律(包括两个判据)1.盖斯定律2.热力学第一定律:△U=Q-W3.热力学第二定律:△S(孤立)= △S(体系)+ △(环境)4.热力学第三定律:0K时,任何纯物质的完美晶体,S=05.两个判据:ⅰ.熵判据:△S(孤立)= △S(体系)+ △S(环境) ………………自发过程△S(孤立)= △S(体系)+ △S(环境) ………………不能进行ⅱ.G判据:等温等压吓,体系的G减小的方向是不能做非体积功的化学反应进行的方向.不及化学反应如此,任何等温等压虾,不做非体积功的自发过程的G都将减小.这正是热力学第二定律的另一种表述形式.△G＜0 …………………自发进行△G＞0 …………………不能自发进行△G=0 …………………可逆发应三.熟练掌握并运用几个热力学攻势(方程式)进行计算1.△U=Q-W2.Q v=△U3.Q p=△HH=U+PV △H=△U+△(PV)4.△r H mθ=∑υB△f H mθ(B)5.△S=Q r/T △r S mθ=∑υB△f S mθ(B)6.△G=△H-T△S 并分析自发进行的四种情况△r G mθ=∑υB△f G mθ(B)四.热力学的标准状态,尤其要注意所给定的热力学条件五.热力学化学方程式的书写六.问题:1.P△V和△(PV)2.H和Q。

第2章 化学热力学基础2-1. 估计下列过程ΔS 、ΔH 、ΔG 的符号。

(1)硫酸溶于水 (2)室温下冰融化 (3)NaNO 3(s)溶于水解：(1)ΔS >0，ΔH <0，ΔG <0；(2)ΔS >0，ΔH >0，ΔG <0；(3)ΔS >0，ΔH >0，ΔG <0。

2-2. 确定下列各组物质熵值的大小顺序。

(1)H 2O(l)、H 2O(g)、H 2O(s)； (3)CH 4(g)、C 2H 6 (g)；(2)H 2(g,310K )、H 2(g ，298K) (4)Fe(s)、Fe 2O 3(s)。

解：(1)S (H 2O,g)>S (H 2O,l)>S (H 2O,s) (2)S (H 2,g,80)>℃S (H 2,g,25)℃(3)S (C 2H 6,g) > S (CH 4,g) (4)S (Fe 2O 3,s)>S (Fe,s)2-3. 计算体系热力学能的变化 (1)体系从环境吸热1000J ，并对环境作功540J ；(2)体系向环境放热535J ，环境对体系作功250J 。

解: (1)ΔU =Q +W =(+1000)+(-540)=460(J)(2)ΔU =Q +W =(-250)+(+535)=285(J)2-4. 求下列反应的Δr H m θ。

[Δf H m θ ( Fe 2O 3,s)=－822.2kJ·mol -1，Δf H m θ ( Al 2O 3,s)=－1670kJ·mol -1，其余Δf H m θ值查附录一 ](1)4NH 3(g) + 5O 2(g) = 4NO(g)+ 6H 2O(g) (2)C 2H 4(g)+ H 2O(g)= C 2H 5OH(l)(3)Fe 2O 3(s)+ 2Al(s) = 2Fe(s)+ Al 2O 3(s)解: (1) Δr H m θ =4Δf H m θ(NO,g)+6Δf H m θ(H 2O,g)-[4Δf H m θ( NH 3,g)+5Δf H m θ(O 2,g)]=4×90.25+6×(-241.8)-[4×(-46.11)+5×0]=-905.36(kJ·mol -1)(2) Δr H m θ=Δf H m θ(C 2H 5OH,l)-[Δf H m θ(C 2H 4,g)+Δf H m θ(H 2O,g)]=-277.7-[(52.26+(-241.8)]=-88.16(kJ·mol -1)(3) Δr H m θ=2Δf H m θ(Fe,s)+ Δf H m θ(Al 2O 3,s)- [Δf H m θ(Fe 2O 3,s)+ 2Δf H m θ(Al,s)]=2×0+(-1670)-[(-822.2)+2×0] = -847.8 kJ·mol -12-5. 已知Δc H m θ(C 3H 8,g)=-2220.9kJ·mol -1，Δf H m θ(H 2O,l)=-285.8kJ·mol -1，Δf H m θ(CO 2,g)=-393.5kJ·mol -1，求C 3H 8(g)的Δf H m θ。

第二章、热力学基础杜勇2.1溶体相的热力学模型2.1.1二元系的摩尔吉布斯自由能2.1.2理想溶液2.1.3混合量2.1.4过剩量2.1.5描述替换溶液的经验方法2.1.6真实溶液2.1.7吉布斯－杜亥姆公式的应用2.1.8稀溶液的近似处理2.1.9两个热力学计算的练习2.2磁性对热力学性质的贡献2.3热力学性质的估算2.4稳定图及其在界面反应用中的应用2.51733到2010年热力学发展的里程碑简介2.6综合练习一:纯元素的热力学性质2.7综合练习二:磁性转变对热力学的贡献2.1溶液的热力学模型2.1.1二元系的摩尔吉布斯自由能图Gαm=x A o GαA+x B o GαB+RT(x A ln x A+x B ln x B)+ex Gαm(4)M Gαm=RT(x A ln x A+x B ln x B)+ex Gαm(5)Partial ideal entropy of mixing:M S i ideal=-R lnx iRT(x A ln x A+x B ln x B)⇒(吉布斯自由能的理想混合熵)A、B两种原子随机分布⇒混合熵-R(xln x A+x B ln x B)A问题一:怎样计算吉布斯自由能的理想混合熵?RT(x A ln x A+x B ln x B)?问题一:怎样计算吉布斯自由能的理想混合熵?RT(x A ln x A+x B ln x B)?答案:A、B两种原子随机分布⇒所有位置等价⇒替代固溶体随机分布的数量可以根据N A个A原子与N B个B原子的数量表述:W=N!/(N A!N B!)(6)根据玻尔兹曼公式,这种随机分布对熵的贡献如下:∆S/κ=ln W=ln N!-∑ln N i!≈N ln N-∑N i ln N i=N ln N–N∑(N i/N)ln N i=-N∑(N i/N)ln(N i/N)=-N∑x i ln x i∆G=-T∆S=N k T∑x i ln x i=RT∑x i ln x i(7) *ln N!=N ln N–N(stalin formula)(when N is very large)2.1溶液的热力学模型2.1.2理想溶液(I)假设随机混合(random mixing)(II)在不同种类原子之间没有特殊的相互作用(no particular interaction)理想溶液的吉布斯自由能与体积:Gαm=x A o GαA+x B o GαB+RT(x A ln x A+x B ln x B)(8) V m=x A o V A+x B o V B(9)问题二:请根据方程(8）推导出方程(9）.RT(x A ln x A+x B ln x B)项对二元系的贡献:RT(x A ln x A+x B ln x B+x C ln x C)项对三元系的贡献:Fig.3通过混合熵确定的(a)二元、(b)三元系的摩尔吉布斯能曲线2.1溶液的热力学模型2.1.3热力学性质的混合量∙相的任意摩尔混合量都可用纯组元热力学性质的加权平均来表示Q m=x A o Q A+x B o Q B+M Q m(10) M Q m是任意摩尔混合量.∙偏混合量是相对于纯组元热力学性质的相对值.M Q A=Q A–o Q A(11) G i=o G i+RT ln x i+RT lnγiQ A=G i,o Q A=o Gi,M Q A=RT ln x i+RT lnγi∙对于理想溶液，混合体积M V m为02.1溶液的热力学模型2.1.4热力学性质的过剩量∙过剩量是相对于理想溶液而言:G m=x A o G A+x B o G B+RT(x A ln x A+x B ln x B)+ex G m(12)∙过剩量为实际溶液与理想溶液的热力学函数的差值∙过剩偏自由能,过剩偏熵,和过剩偏焓（混合焓）:ex G j=ex G m+∂ex G m/∂x j-∑x i∂ex G m/∂x i(13) ex G i=G i-o G i+T M s i ideal(14) ex S i=S i-o S i-M s i ideal(15) ex H i=H i-o H i=M H i(16) M s i ideal=-Rlnx i(partial ideal entropy of mixing)M H i ideal=0:(partial ideal enthalpy of mixing)2.1溶液的热力学模型2.1.5描述替换溶液的经验方法∙过剩吉布斯自由能:实际溶液与理想溶液吉布斯自由能的差ex G m=x A x B I 纯组元时为零∙ex G m通常由Redlich-Kister公式表示:I=0L+(x A-x B)⨯1L+(x A-x B)2⨯2L+ (17)∙I的物理意义:两个组元间的相互作用.∙I=0:理想溶液;I=恒量(不随成分、温度变化):规则溶液参数(regular solution parameter)；1L:亚规则溶液参数(sub-regular solution parameter);2L:亚亚规则溶液参数(sub-sub-regular solution parameter)；2.1溶液的热力学模型2.1.5描述替换溶液的经验方法ex G m=x A x B(0L+(x A-x B)⨯1L+(x A-x B)2⨯2L)Fig.4Properties of Redlich-Kister termsm A B A B A Bi L=a i+b i TFig.1具有反常溶解度间隙的Fe-Zn相图m A B A B A Bi L=h i⨯exp(-T/s i)G.Kaptay,CALPHAD,28,115-124(2004)Fig.2无反常溶解度间隙的Fe-Zn相图2.1.6实际溶液Fig.5三种不同相互作用参数的二元系规则溶液模型.2.1.7吉布斯－杜亥姆关系的应用∙T和P为常量时,吉布斯－杜亥姆关系归结为:∑x i d lna i=0(20)∑x i d lnf i=0(21)问题四:怎样由方程（20）得出方程（21）?∙在二元系中,吉布斯－杜亥姆关系采用下面的公式:x A dln a A+x B dln a B=0(22)∙吉布斯－杜亥姆关系的重要性:♠在二元系中，一个组元的活度可以由另一个已测的组元活度计算出。

普通化学第二章化学热力学基础⏹§1.1 热力学基本概念⏹§1.2 热力学第一定律⏹§1.3 焓热力学⏹§1.4 自发过程和熵⏹§1.5 吉布斯自由能与化学反应的方向⏹总结化学热力学研究与解决的主要问题？热力学-------研究各种形式的能量相互转变过程中所遵循规律的科学。

热力学的基础：热力学第一定律和热力学第二定律化学热力学-------将热力学的原理应用于化学变化过程，就称为化学热力学。

化学热力学研究与解决的主要问题：一是在指定的条件下，某一化学反应进行时，与外界交换多少能量？即计算化学反应热。

二是在指定的条件下，某一化学反应能否自发进行，即判断化学反应进行的方向。

三若可能自发进行，反应进行的温度如何？热力学方法的特点：大量质点组成的宏观体系1、热、功、状态函数△U、△H、△G和△S2、热力学第一、二、三定律3、盖斯定律4、自发过程的判定5、吉布斯—亥姆霍兹公式1、功、热、内能、焓、自由能、熵的计算2、自发过程判定AgNO 3与NaCl 的水溶液:如果只研究在水溶液中所进行的反应，则含有这两种物质的水溶液就是体系。

溶液以外的烧杯、溶液上方的空气都是环境。

如果还要研究反应时的能量变化，则水溶液和烧杯为体系，空气为环境。

例如:NaCl+AgNO 3溶液－体系分类敞开体系：体系与环境之间既有能量交换，又有物质交换。

封闭体系：体系与环境之间只有能量交换，没有物质交换。

孤立体系：体系与环境之间既没有能量交换，也没有物质交换。

敞开体系封闭体系绝热箱孤立体系NaOH+H2ONaOH+H2ONaOH+H2O热物质热二、体系的性质1、体系的性质：确定体系状态的各种宏观物理量。

如温度、压力、体积、质量、密度、浓度等2、体系的性质分为广度性质和强度性质两类：广度性质：在数值上与体系中物质的量成正比，即具有加和性。

如体积、质量、内能、焓、熵等。

强度性质：在数值上与体系中物质的量无关，即不具有加和性。