制程能力(Cpk)分析教程.
- 格式:doc
- 大小:286.50 KB
- 文档页数:14

C PK 培訓教材一.Cpk 的定義某一制程在一定因素與正常管制狀態下的品質作業能力.二.Cpk 的影響因素製程要因--—原料,机器設備,人員能力,測量儀器.製程條件-——常態分配,統計管制狀態。
三。
Cpk 的計算USL :上限尺寸L SL:下限尺寸Ave ra ge:測量數据的平均值σ:標準差,其公式為: σ=1/)(22--∑∑n n x xCpu=(USL —Average)/3σCp l=(Average-L SL )/3σCpk=Min(Cpu,C pl) σ:其大小表示測量數据的離散程度, σ越小表示數据的離散程度越小,反之則數据的離散程度越大.C pu:其值表示測量數据偏離上限的程度, Cpu 越大表示測量數据偏離上限較遠; 反之則數据靠近上限。
Cpl: 其值表示測量數据偏離下限的程度, C pl 越大表示測量數据偏離下限較遠; 反之則數据靠近下限。
四.Cp k的等級A : 1.33≦C pkA 級,製程能力滿足圖紙要求,生產中几乎沒有不良品產生。
B: 1。
00≦Cpk〈1.33B級,製程能力基本滿足圖紙要求,生產中約有0。
27%不良品產生,必須加以注意,並設法維持不使其變坏。
C: Cpk<1.00C級,製程能力不能滿足圖紙要求,生產中可能有較多不良品產生, 應採取緊急措施,全面檢討所有可能影響的因素,必要時得停止生產。
五.Cpk 管制抽樣的基本原則管制方法取樣頻率管制圖查檢表高 1—-2小時15——30分鐘中 4-—8小時每小時低每班次 2小時六.CPK數据分析.1.數据均分布于中值兩旁, Cpk值一般大于1。
33,見附圖1. 2。
數据离散地分布中值兩旁,Cpk值一般小于1.33,見附圖2.3。
數据分布离散度小,但偏中值不遠,Cpk值大于1.33,見附圖3。
4.數据分布离散度小,但偏中值較遠,Cpk值小于1.33. 見附圖4.5。
數据絕大多數雖均分布于中值兩旁,但個別超差,將大大降低Cpk值,甚至Cpk值小于1。

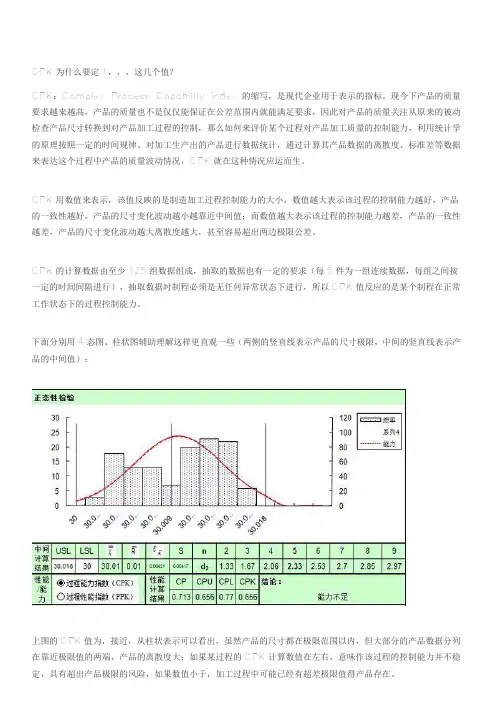
CPK为什么要定1,,,这几个值?CPK:Complex Process Capability index 的缩写,是现代企业用于表示的指标。
现今下产品的质量要求越来越高,产品的质量也不是仅仅能保证在公差范围内就能满足要求,因此对产品的质量关注从原来的被动检查产品尺寸转换到对产品加工过程的控制,那么如何来评价某个过程对产品加工质量的控制能力,利用统计学的原理按照一定的时间规律、对加工生产出的产品进行数据统计,通过计算其产品数据的离散度、标准差等数据来表达这个过程中产品的质量波动情况,CPK就在这种情况应运而生。
CPK用数值来表示,该值反映的是制造加工过程控制能力的大小,数值越大表示该过程的控制能力越好,产品的一致性越好,产品的尺寸变化波动越小越靠近中间值;而数值越大表示该过程的控制能力越差,产品的一致性越差,产品的尺寸变化波动越大离散度越大,甚至容易超出两边极限公差。
CPK的计算数据由至少125组数据组成,抽取的数据也有一定的要求(每5件为一组连续数据,每组之间按一定的时间间隔进行),抽取数据时制程必须是无任何异常状态下进行,所以CPK值反应的是某个制程在正常工作状态下的过程控制能力。
下面分别用4态图、柱状图辅助理解这样更直观一些(两侧的竖直线表示产品的尺寸极限,中间的竖直线表示产品的中间值):上图的CPK值为,接近,从柱状表示可以看出,虽然产品的尺寸都在极限范围以内,但大部分的产品数据分列在靠近极限值的两端,产品的离散度大;如果某过程的CPK计算数值在左右,意味作该过程的控制能力并不稳定,具有超出产品极限的风险,如果数值小于,加工过程中可能已经有超差极限值得产品存在。
上图的CPK值为,与CPK值为的图形对比可以看出,产品的尺寸的波动范围比前一副图约小一点,更趋近中间值。
因此当CPK值增大时,该图反应出的过程控制能力就比CPK值为的过程控制能力要好,那么产品超差两端极限的情况也就更小。
下面分别为CPK值为和左右的图形从上列4张图片的对比不难看出,当CPK值越大时,过程控制能力越强,加工出的产品越靠近中间值且波动范围越小,产品互换性好质量越高。
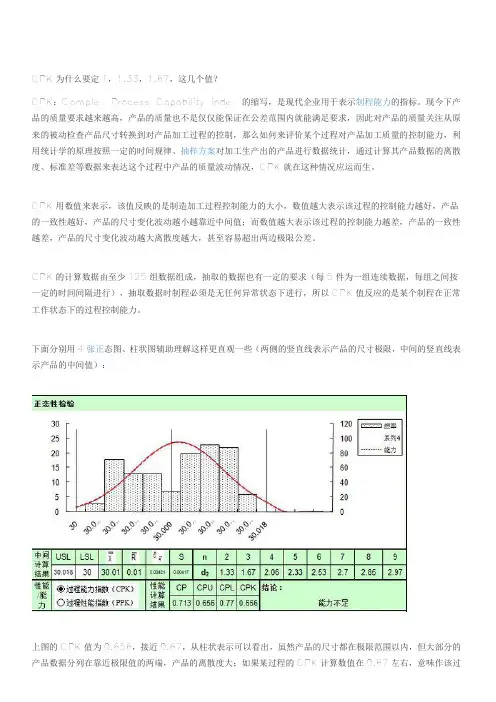
CPK为什么要定1,1.33,1.67,这几个值?CPK:Complex Process Capability index 的缩写,是现代企业用于表示制程能力的指标。
现今下产品的质量要求越来越高,产品的质量也不是仅仅能保证在公差范围内就能满足要求,因此对产品的质量关注从原来的被动检查产品尺寸转换到对产品加工过程的控制,那么如何来评价某个过程对产品加工质量的控制能力,利用统计学的原理按照一定的时间规律、抽样方案对加工生产出的产品进行数据统计,通过计算其产品数据的离散度、标准差等数据来表达这个过程中产品的质量波动情况,CPK就在这种情况应运而生。
CPK用数值来表示,该值反映的是制造加工过程控制能力的大小,数值越大表示该过程的控制能力越好,产品的一致性越好,产品的尺寸变化波动越小越靠近中间值;而数值越大表示该过程的控制能力越差,产品的一致性越差,产品的尺寸变化波动越大离散度越大,甚至容易超出两边极限公差。
CPK的计算数据由至少125组数据组成,抽取的数据也有一定的要求(每5件为一组连续数据,每组之间按一定的时间间隔进行),抽取数据时制程必须是无任何异常状态下进行,所以CPK值反应的是某个制程在正常工作状态下的过程控制能力。
下面分别用4张正态图、柱状图辅助理解这样更直观一些(两侧的竖直线表示产品的尺寸极限,中间的竖直线表示产品的中间值):上图的CPK值为0.656,接近0.67,从柱状表示可以看出,虽然产品的尺寸都在极限范围以内,但大部分的产品数据分列在靠近极限值的两端,产品的离散度大;如果某过程的CPK计算数值在0.67左右,意味作该过程的控制能力并不稳定,具有超出产品极限的风险,如果数值小于0.67,加工过程中可能已经有超差极限值得产品存在。
上图的CPK值为1.078,与CPK值为0.656的图形对比可以看出,产品的尺寸的波动范围比前一副图约小一点,更趋近中间值。
因此当CPK值增大时,该图反应出的过程控制能力就比CPK值为0.656的过程控制能力要好,那么产品超差两端极限的情况也就更小。

CPK (Process CapabilityIndex )的定义:制程能力指数;ﻫCPK的意义:制程水平的量化反映;(用一个数值来表达制程的水平)制程能力指数:是一种表示制程水平高低的方便方法,其实质作用是反映制程合格率的高低。
与CPK相关的几个重要概念:USL (Upper Specification Limit): 即规格上限;ﻫLSL (Lower Specification Li mit): 即规格下限;C (Center Line):规格中心;ﻫ=(X1+X2+……+Xn)/n 平均值;(n为样本数)T=USL-LSL:即规格公差;δ(sigma)为数据的标准差。
标准差是一组数据平均值分散程度的一种度量。
一个较大的标准差,代表大部分数值和其平均值之间差异较大;一个较小的标准差,代表这些数值较接近平均值。
例如,A、B两组各有6位学生参加同一次语文测验,A组的分数为95、85、75、65、55、45,B 组的分数为73、72、71、69、68、67。
这两组的平均数都是70,但A组的标准差约为17.08分,B 组的标准差约为2.16分,说明A组学生之间的差距要比B组学生之间的差距大得多。
ﻫ(Excel中的“ST DEV”函数自动计算所取样数据的标准差(σ) )样本: 从总体中随机抽取的若干个个体的总和称为样本。
组成样本的每个个体称为样品。
样本标准偏差S: 因为标准偏差是用数据整体计算,所以当数据量大太时,就不便以操作,而且不符合现场需要。
所以一般情况下,会用样本标准偏差S来代替σ。
S ≈σﻫCa (Capability of Accuracy):制程准确度,Ca衡量的是“实际平均值“与“规格中心值”的一致性;ﻫ1.对于单边规格,不存在规格中心,因此也就不存在Ca;2.对于双边规格: ﻫCa等级评定及处理原则:A:作业员依作业标准.继续维持.B:有必要时.尽可能改为A级.C:作业员可能看错规格或未照作业标准操作,应加强训练,检讨规格及作业标准.D: 应采取紧急措施.全面检讨可能影响因素.必要时停产.准确度Ca Capability ofAccuracy:代表制程平均值偏离规格中心值之程度。


CPK为什么要定1,1.33,1.67,这几个值?CPK:Complex Process Capability index 的缩写,是现代企业用于表示制程能力的指标。
现今下产品的质量要求越来越高,产品的质量也不是仅仅能保证在公差范围内就能满足要求,因此对产品的质量关注从原来的被动检查产品尺寸转换到对产品加工过程的控制,那么如何来评价某个过程对产品加工质量的控制能力,利用统计学的原理按照一定的时间规律、抽样方案对加工生产出的产品进行数据统计,通过计算其产品数据的离散度、标准差等数据来表达这个过程中产品的质量波动情况,CPK就在这种情况应运而生.CPK用数值来表示,该值反映的是制造加工过程控制能力的大小,数值越大表示该过程的控制能力越好,产品的一致性越好,产品的尺寸变化波动越小越靠近中间值;而数值越大表示该过程的控制能力越差,产品的一致性越差,产品的尺寸变化波动越大离散度越大,甚至容易超出两边极限公差.CPK的计算数据由至少125组数据组成,抽取的数据也有一定的要求(每5件为一组连续数据,每组之间按一定的时间间隔进行),抽取数据时制程必须是无任何异常状态下进行,所以CPK值反应的是某个制程在正常工作状态下的过程控制能力。
下面分别用4张正态图、柱状图辅助理解这样更直观一些(两侧的竖直线表示产品的尺寸极限,中间的竖直线表示产品的中间值):上图的CPK值为0。
656,接近0.67,从柱状表示可以看出,虽然产品的尺寸都在极限范围以内,但大部分的产品数据分列在靠近极限值的两端,产品的离散度大;如果某过程的CPK计算数值在0。
67左右,意味作该过程的控制能力并不稳定,具有超出产品极限的风险,如果数值小于0.67,加工过程中可能已经有超差极限值得产品存在。
上图的CPK值为1.078,与CPK值为0.656的图形对比可以看出,产品的尺寸的波动范围比前一副图约小一点,更趋近中间值.因此当CPK值增大时,该图反应出的过程控制能力就比CPK值为0。




工序能力指数CPK的计算和分析CPK的计算公式如下:CPK = min(USL - μ,μ - LSL)/(3 * σ)其中,USL为规格上限,LSL为规格下限,μ为平均值,σ为标准差。
CPK的值越大,表示工序的稳定性和可控性越强。
一般来说,CPK值大于1.33被认为是良好的,大于1.67则被认为是极好的。
而CPK值小于1则表示工序不稳定或者不可控。
CPK的分析可以从以下几个方面进行:1.变异性分析:通过计算标准差和绘制控制图来评估工序的变异性。
如果标准差较小,并且控制图上的数据点在控制界限内,则说明工序具有较小的变异性,可以认为是稳定的。
反之,则说明工序存在较大的变异性,需要进一步改进。
2.规格限值分析:通过比较规格限值和平均值,以及计算CPK值,来评估工序是否能够满足产品的规格要求。
如果CPK值大于1,则说明工序具有足够的能力满足规格要求。
如果CPK值小于1,则需要进行进一步的改进,以提高工序的能力。
3.误差源分析:通过分析工序中可能存在的误差源,找出和改进引起工序不稳定的原因。
误差源可能包括人为因素、设备问题、材料质量等。
通过改进和优化这些误差源,可以提高工序的稳定性和可控性。
4.过程能力改进:通过改进工序中的控制措施和方法,来提高工序的能力。
例如,可以采用六西格玛等质量管理工具,优化工序的流程和参数设定,以减少变异性和提高工序的能力。
总之,CPK是评估工序稳定性和可控性的重要指标,可以通过计算和分析CPK值来评估工序的能力,并通过改进控制措施和优化过程来提高工序的能力。
CPK的计算及分析方法
CPK是一种统计工具,用于度量一个过程是否处于受控状态。
它是根据过程的规格界限和过程数据的方差来计算的。
CPK的计算及分析方法主要包括以下步骤:
1.确定规格界限:首先需要确定所分析的过程的规格界限,即最大和最小允许的值。
规格界限可以是设计规格,也可以是客户要求的规格。
2.收集过程数据:收集足够的过程数据以计算CPK。
数据可以是过程输出的测量值,例如长度、重量、时间等。
3.计算过程平均值:计算过程数据的平均值,并将其标记为μ。
4.计算过程标准差:计算过程数据的标准差,并将其标记为σ。
5.计算过程能力指数:根据以下公式计算过程的能力指数:
5.1上限CPK=(规格界限上限-μ)/(3σ)
5.2下限CPK=(μ-规格界限下限)/(3σ)
CPK取较小值,即上限CPK和下限CPK中的较小值。
6.判断能力指数的满足程度:根据计算得到的CPK值,可以判断过程的能力。
-CPK值大于1:过程的能力较好,可以满足规格界限的要求。
-CPK值等于1:过程的能力较差,只能满足规格界限的要求。
-CPK值小于1:过程的能力很差,无法满足规格界限的要求。
7.数据分析和改进:根据CPK值,分析过程是否能够满足要求。
如果CPK值小于1,说明过程存在问题,需要进行改进。
可以通过改进流程、提高设备性能、培训操作员等方式来提高过程能力。