2017全国三卷理科数学高考真题与答案
- 格式:doc
- 大小:812.00 KB
- 文档页数:15
绝密★启用前2017年普通高等学校招生全国统一考试(新课标Ⅲ)理科数学注意事项: 1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
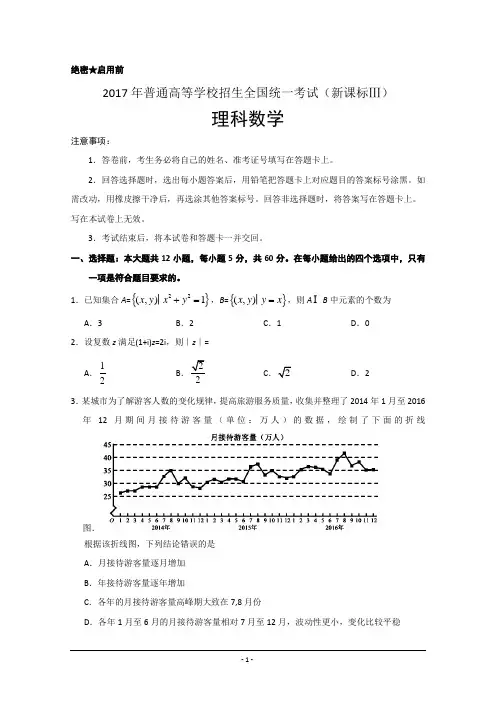
1.已知集合A ={}22(,)1x y x y +=│,B ={}(,)x y y x =│,则A B 中元素的个数为 A .3B .2C .1D .02.设复数z 满足(1+i)z =2i ,则∣z ∣=A .12B C D .23.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是 A .月接待游客量逐月增加 B .年接待游客量逐年增加C .各年的月接待游客量高峰期大致在7,8月份D .各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳4.(x +y )(2x -y )5的展开式中x 3y 3的系数为 A .-80B .-40C .40D .805.已知双曲线C :22221x y a b -= (a >0,b >0)的一条渐近线方程为y x =,且与椭圆221123x y +=有公共焦点,则C 的方程为 A .221810x y -=B .22145x y -= C .22154x y -= D .22143x y -= 6.设函数f (x )=cos(x +3π),则下列结论错误的是 A .f (x )的一个周期为−2πB .y =f (x )的图像关于直线x =83π对称 C .f (x +π)的一个零点为x =6π D .f (x )在(2π,π)单调递减 7.执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为A .5B .4C .3D .28.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为 A .πB .3π4C .π2D .π49.等差数列{}n a 的首项为1,公差不为0.若a 2,a 3,a 6成等比数列,则{}n a 前6项的和为A .-24B .-3C .3D .810.已知椭圆C :22221x y a b+=,(a >b >0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为ABC.3D .1311.已知函数211()2()x x f x x x a e e --+=-++有唯一零点,则a =A .12-B .13C .12D .112.在矩形ABCD 中,AB=1,AD=2,动点P 在以点C 为圆心且与BD 相切的圆上.若AP=λAB +μAD,则λ+μ的最大值为A .3B .CD .2二、填空题:本题共4小题,每小题5分,共20分。

2016年普通高等学校招生全国统一考试理科数学一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)设集合S = ,则S T ={}{}(x 2)(x 3)0,T 0S x x x =--≥=I >P I (A) [2,3] (B)(- ,2] [3,+)∞U ∞(C) [3,+) (D)(0,2] [3,+)∞U ∞(2)若z=1+2i ,则 41i zz =-(A)1 (B) -1 (C) i (D)-i(3)已知向量 , 则ABC=1(2BA =u u v 1),2BC =u u u v ∠(A)300 (B) 450 (C) 600 (D)1200(4)某旅游城市为向游客介绍本地的气温情况,绘制了一年中月平均最高气温和平均最低气温的雷达图。
图中A 点表示十月的平均最高气温约为150C ,B 点表示四月的平均最低气温约为50C 。
下面叙述不正确的是(A) 各月的平均最低气温都在00C 以上(B) 七月的平均温差比一月的平均温差大(C) 三月和十一月的平均最高气温基本相同(D) 平均气温高于200C 的月份有5个(5)若 ,则 3tan 4α=2cos 2sin 2αα+=(A) (B) (C) 1 (D) 642548251625(6)已知,,,则432a =344b =1325c =(A ) (B )(C )(D )b a c <<a b c <<b c a <<c a b<<(7)执行下图的程序框图,如果输入的a =4,b =6,那么输出的n =(A )3(B )4(C )5(D )6(8)在中,,BC 边上的高等于,则 ABC △π4B =13BC cos A =(A (B(C )(D )-- (9)如图,网格纸上小正方形的边长为1,粗实现画出的是某多面体的三视图,则该多面体的表面积为(A)18+(B )54+(C )90(D )81(10) 在封闭的直三棱柱ABC -A 1B 1C 1内有一个体积为V 的球,若AB BC ,AB =6,BC =8,AA 1=3,则V 的最大值是⊥(A )4π (B )(C )6π92π(D ) 323π(11)已知O 为坐标原点,F 是椭圆C :的左焦点,A ,B 分别为C 的左,右顶点.P 为22221(0)x y a b a b+=>>C 上一点,且PF ⊥x 轴.过点A 的直线l 与线段PF 交于点M ,与y 轴交于点E .若直线BM 经过OE 的中点,则C 的离心率为(A )(B )(C )(D )13122334(12)定义“规范01数列”{a n }如下:{a n }共有2m 项,其中m 项为0,m 项为1,且对任意,2k m ≤中0的个数不少于1的个数.若m =4,则不同的“规范01数列”共有12,,,k a a a (A )18个 (B )16个 (C )14个 (D )12个二、填空题:本大题共3小题,每小题5分(13)若x ,y 满足约束条件 则z=x+y 的最大值为_____________.{x ‒y +1≥0x ‒2y ≪0x +2y ‒2≪0(14)函数的图像可由函数的图像至少向右平移_____________个单位长y =sin x ‒3cos x y =sin x +3cos x 度得到。

1 2017高考全国III
卷理数1.已知集合A=22(,)1x y x y │
,B=(,)x y y x │,则A B 中元素的个数为A .3 B .2 C .1
D .0 2.设复数z 满足(1+i)z=2i ,则∣z ∣=
A .12
B .2
2C .2D .2
3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图根据该折线图,下列结论错误的是
A .月接待游客量逐月增加
B .年接待游客量逐年增加
C .各年的月接待游客量高峰期大致在
7,8月份D .各年1月至6月的月接待游客量相对
7月至12月,波动性更小,变化比较平稳4.(x +y )(2x -y )5的展开式中x 3y 3的系数为
A .-80
B .-40
C .40
D .80 5.已知双曲线C :22221x
y a b (a >0,b >0)的一条渐近线方程为5
2y x ,且与椭圆
22
112
3x y 有公共焦点,则C 的方程为
A .221810x y
B .22
145x y C .22
154x y D .22
1
43x y 6.设函数f(x)=cos(x+3),则下列结论错误的是
A .f(x)的一个周期为-2π
B .y=f(x)的图像关于直线x=8
3对称。
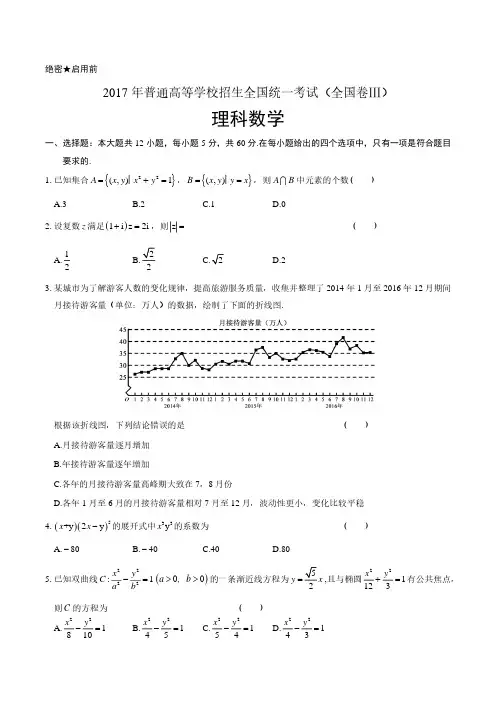
绝密★启用前2017年普通高等学校招生全国统一考试(全国卷Ⅲ)理科数学一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}22(,)1A x y x y =+=│,{}(,)B x y y x ==│,则A B 中元素的个数( )A.3B.2C.1D.0 2.设复数z 满足()1i z 2i +=,则z =( )A.12B.2D.23.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是 ( )A.月接待游客量逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7,8月份D.各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳 4.()()5+y 2y x x −的展开式中33y x 的系数为 ( )A.−80B.−40C.40D.805.已知双曲线2222:1x y C a b−=()00>>a b ,的一条渐近线方程为2y x =,且与椭圆221123x y +=有公共焦点,则C 的方程为( )A.221810x y −= B.22145x y −= C.22154x y −= D.22143x y −=6.设函数()π3cos ⎛⎫=+ ⎪⎝⎭f x x ,则下列结论错误的是( )A.()f x 的一个周期为2π−B.()f x 的图像关于直线8π=3x 对称 C.()π+f x 的一个零点为π6=xD.()f x 在(π2,π)单调递减7.执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为( )A.5B.4C.3D.28.已知圆柱的高为1,它的两个底面的圆周在直径2的同一个球的球面上,则该圆柱的体积为( )A.πB.3π4C.π2D.π49.等差数列{}n a 的首项为1,公差不为0.若236a a a ,,成等比数列,则{}n a 前6项的和为( )A.24−B.3−C.3D.810.已知椭圆C :22221x y a b+=()0a b >>的左、右顶点分别为1A ,2A ,且以线段12A A 为直径的圆与直线20bx ay ab −+=相切,则C 的离心率为( )A.3B.3C.3D.1311.已知函数211()2(e e )−−+=−++x x f x x x a 有唯一零点,则a =( )A.12−B.13C.12D.112.在矩形ABCD 中,12AB AD ==,,动点P 在以点C 为圆心且与BD 相切的圆上.若AP=AB+AD λμ,则λμ+的最大值为( ) A.3D.2二、填空题:本题共4小题,每小题5分,共20分.13.若x ,y 满足约束条件y 0,20,0,x x y y −≥⎧⎪+−≤⎨⎪≥⎩则z 34x y =−的最小值为 .14.设等比数列{}n a 满足1213–1,3a a a a +==−−,则4=a .15.设函数1,0,()2,0,x x x f x x +≤⎧=⎨>⎩则满足1()()12f x f x +−>的x 的取值范围是 .16.a b ,为空间中两条互相垂直的直线,等腰直角三角形ABC 的直角边AC 所在直线与a b ,都垂直,斜边AB 以直线AC 为旋转轴旋转,有下列结论:①当直线AB 与a 成60︒角时,AB 与b 成30︒角; ②当直线AB 与a 成60︒角时,AB 与b 成60︒角; ③直线AB 与a 所成角的最小值为45︒; ④直线AB 与a 所成角的最大值为60︒.其中正确的是 .(填写所有正确结论的编号)三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:共60分. 17.(12分)ABC △的内角AB C ,,的对边分别为a b c ,,,已知sin 0+=A A,a ,2b =. (1)求c ;(2)设D 为BC 边上一点,且AD AC ⊥,求ABD △的面积.某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:以最高气温位于各区间的频率代替最高气温位于该区间的概率. (1)求六月份这种酸奶一天的需求量X (单位:瓶)的分布列;(2)设六月份一天销售这种酸奶的利润为Y (单位:元),当六月份这种酸奶一天的进货量n (单位:瓶)为多少时,Y 的数学期望达到最大值? 19.(12分)如图,四面体ABCD 中,ABC △是正三角形,ACD △是直角三角形,.ABD CBDAB BD ∠=∠=,(1)证明:平面ACD ⊥平面ABC ;(2)过AC 的平面交BD 于点E ,若平面AEC 把四面体ABCD 分成体积相等的两部分,求二面角––D AE C 的余弦值.已知抛物线C :22y x =,过点(2,0)的直线l 交C 与,A B 两点,圆M 是以线段AB 为直径的圆. (1)证明:坐标原点O 在圆M 上;(2)设圆M 过点P (4,−2),求直线l 与圆M 的方程.21.(12分)已知函数1(n )l =−−f x a x x . (1)若()0f x ≥,求a 的值;(2)设m 为整数,且对于任意正整数n ,21111+1+1+222n m ⎛⎫⎛⎫⎛⎫⎪⎪⎪⎝⎭⎝⎭⎝⎭<,求m 的最小值.________________ _____________(二)选考题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分. 22.[选修4−4:坐标系与参数方程](10分)在直角坐标系xOy 中,直线1l 的参数方程为2+,,x t y kt =⎧⎨=⎩(t 为参数),直线2l 的参数方程为2,,x m my k =−+⎧⎪⎨=⎪⎩(m 为参数).设1l 与2l 的交点为P ,当k 变化时,P 的轨迹为曲线C . (1)写出C 的普通方程;(2)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,设3l : ()cos si n ρθθ+,M 为3l 与C 的交点,求M 的极径.23.[选修4−5:不等式选讲](10分)已知函数12f x x x =+−−(). (1)求不等式1f x ≥()的解集; (2)若不等式2– f x x x m ≥+()的解集非空,求m 的取值范围.2017年普通高等学校招生全国统一考试(全国卷Ⅲ)A B 中元素的个数为()()(2i 1i 1i 1i −+−3.【答案】A【解析】根据折线图可知,2014年8月到9月、2014年10月到11月等月接待游客量都是减少,所以A 错误. 4.【答案】C【解析】当第一个括号内取x 时,第二个括号内要取含23x y 的项,即()()23352C x y −,当第一个括号内取y 时,第二个括号内要取含32x y的项,即()()32252C x y −,所以33x y 的系数为()23325522108440C C ⨯−⨯=⨯−=.5.【答案】B【解析】根据双曲线C 的渐近线方程为2y x =,可知2b a = ①,又椭圆221123x y +=的焦点坐标为(3,0)和(3−,0),所以229a b += ②,根据①②可知224,5a b ==,所以选B. 6.【答案】D【解析】根据函数解析式可知函数()f x 的最小正周期为2π,所以函数的一个周期为π2−,A 正确;当8ππ,3π33=+=x x ,所以πcos 13⎛⎫+=− ⎪⎝⎭x ,所以B 正确;()4cos cos 33ππππ⎛⎫⎛⎫+=++=+ ⎪ ⎪⎝⎭⎝⎭f x x x ,当π6=x 时,4π3π32+=x ,所以()π0+=f x ,所以C 正确;函数()πcos 3⎛⎫=+ ⎪⎝⎭f x x 在(π2,23π)上单调递减;(23π,π)上单调递增,故D 不正确.所以选D .7.【答案】D【解析】010*******,100911001090,13S M t S M t =+==−==−===,,>;,,90<91,输出S ,此时,3t =不满足t N ≤,所以输入的正整数N 的最小值为2,故选D. 8.【答案】B【解析】设圆柱的底面半径为r ,则22213=1=24r ⎛⎫− ⎪⎝⎭,所以,圆柱的体积33=π1=π44⨯V ,故选B.9.【答案】A【解析】设等差数列n a 的公差为d ,因为236,,a a a 成等比数列,所以2263a a a =,即()()()211152a d a d a d ++=+,又11a =,所以220d d +=,又0,d ≠则2d =−,所以6159a a d =+=−,所以n a 的前6项的和6196242S −=⨯=−,故选A. 10.【答案】A以线段12A A 为直径的圆的方程为222x y a +=,由原点到直线20bx ay ab −+=的距离==d a ,得223a b =,所以C 的离心率3e ==.11.【答案】C【解析】由()()2112x x f x x x a ee −−+=−++,得()()()()()()2212121121122224422x x x x x x f x x x a e e x x x a e e x x a e e −−+−−−−−−⎡⎤−=−−−++=−++++=−++⎣⎦,所以()()2f x f x −=,即1x =为()f x 图像的对称轴.由题意()f x 有唯一零点,所以()f x 的零点只能为1x =,即()()2111111210f a ee −−+=−⨯++=,解得12a =.故选C. 12.【答案】A【解析】以A 为坐标原点,AB AD ,所在直线分别为x ,y 轴建立如图所示的平面直角坐标系,则A (0,0),B (1,0),C (1,2),D (0,2),可得直线BD 的方程为220x y +−=,点C 到直线BD 的距=,圆C :()()224125x y −+−=,因为P 在圆C 上,所以P (1cos 5θ+,2θ+)(1,0)AB =,(0,2)AD =,(,2)AP AB AD λμλμ=+=,所以122{θλθμ==()22sin 3λμθθθα+==++≤,tan 2α=,选A.13.【答案】1−【解析】作出约束条件表示的可行域如图中阴影部分所示,作出直线:340l x y −=,平移直线l ,当直线34z x y =−经过点A (1,1)时,z 取得最小值,最小值为341−=−.14.【答案】8−【解析】设等比数列{}n a 的公比为q ,则121(1)1a a a q +=+=−,2131(1)3a a a q −=−=−,两式相除,得21113q q +=−,解得12,1q a =−=,所以3418a a q ==−. 15.【答案】∞1(-,+)4【解析】当0x >,()=21xf x >恒成立,当102x −>,即12x >时,121()=212x f x −−>,当102x −≤,即102x ≤<时,111()=222f x x −+>,则不等式1()()12f x f x +−>恒成立.当0x ≤时,113()()121222+−=+++=+f x f x x x x >,所以104x −≤<.综上所述,x 的取值范围是(14−,+∞).16.【答案】②③【解析】由题意知,,,a b AC 三条直线两两相互垂直,画出图形如图.不妨设图中所示正方体的棱长为1,则1,AC AB ==,斜边AB 以直线AC 为旋转轴旋转,则A 点保持不变,B 点的运动轨迹是以C 为圆心,l 为半径的圆.以C 为坐标原点,以CD 的方向为x 轴正方向,CB 方向为y 轴正方向,CA 的方向为z 轴正方向建立空间直角坐标系.则D (1,0,0),A (0,0,1), 直线a 的单位方向向量(0,1,0), 1.a a ==B 点起始坐标为(0,1,0),直线b 的单位方向向量b (1,0,0), 1.b == 设B 点在运动过程中的坐标B'(cos ,sin ,0)θθ, 其中θ为'CB 与CD 的夹角,[0,2)θπ∈.那么AB'在运动过程中的向量'(cos ,sin ,1),'2AB AB θθ=−=.设直线AB'与a 所成的夹角为[0,2],απ∈(cos ,sin ,1)(0,1,0)cos [0,],2a ABθθαθ−⋅==∈故[,],42ππα∈所以③正确,④错误. 设直线AB'与b 所成的夹角为β,则[0,2],βπ∈ 'bcos 'AB b AB β⋅=(cos ,sin ,1)(1,0,0)'b AB θθ−⋅= .θ 当'AB 与a 成60︒角时,=3πα,1sin =322πθα 因为22sin +cos =1,θθ 所以cos =2θ 所以1cos =.2βθ 因为[0,2],βπ∈所以=3πβ,此时'AB 与b 成60︒角.所以②正确,①错误.三、解答题17.【答案】解:(1)由已知得tan =A 所以2π3A=. 在ABC 中,由余弦定理得22π2844cos 3=+−c c ,即2+224=0c c −. 解得c 6=−,(舍去),c =4 (2)由题设可得π=2∠CAD ,所以π6∠=∠−∠=BAD BAC CAD . 故ABD 面积与ACD 面积的比值为1πsin 26112AB AD AC AD= 又ABC 的面积为142sin 2BAC⨯⨯∠=所以ABD ∆【解析】(1))先求出角A ,再根据余弦定理求出c 即可;(2)根据ABD ,ACD ,ABC 的面积之间的关系求解即可. 18.【答案】解:(1)由题意知,X 所有的可能取值为200,300,500,由表格数据知()2162000.290P X +===, ()363000.490P X ===,()25745000.490P X ++===. 因此X 的分布列为(2200,因此只需考虑200500n ≤≤ 当300500n ≤≤时,若最高气温不低于25,则642Y n n n =−=;若最高气温位于区间[)20,,25,则63002300412002;Y n n n =⨯+−−=−() 若最高气温低于20,则6200220048002;Y n n n =⨯+−−=−() 因此()20.4120020.480020.26400.4.EY n n n n =⨯+−⨯+−⨯=−() 当200300n <≤时,若最高气温不低于20,则642;Y n n n =−=若最高气温低于20,则6200220048002;Y n n n =⨯+−−=−() 因此()()20.40.480020.2160 1.2.EY n n n =⨯++−⨯=+所以300n =时,Y 的数学期望达到最大值,最大值为520元.【解析】(1)根据表格提供的数据进行分类求解即可;(2)根据分布列得到关于利润的函数表达式,进而求解最值.19.解:(1)由题设可得,,ABD CBD ∆≅∆从而AD DC =.又ACD ∆是直角三角形,所以0=90ACD ∠.取AC 的中点O ,连接,,DO BO 则,.DO AC DO AO ⊥=又由于ABC ∆是正三角形,故BO AC ⊥.所以DOB ∠为二面角D AC B −−的平面角.在Rt AOB ∆中,222BO AO AB +=.又AB BD =,所以222222BO DO BO AO AB BD +=+==,故0∠DOB=90.所以平面ACD ⊥平面ABC .(2)由题设及(1)知,OA,OB,OD 两两垂直,以O 为坐标原点,OA 的方向为x 轴正方向,OA 为单位长,建立如图所示的空间直角坐标系O xyz -,则−(1,0,0),(0(1,0,0),(0,0,1)A B C D .由题设知,四面体ABCE 的体积为四面体ABCD 的体积的12,从而E 到平面ABC 的距离为D 到平面ABC 的距离的12,即E 为DB 的中点,得1022E ⎛⎫ ⎪ ⎪⎝⎭,,,故 ()()11,0,1,2,0,0,1,,22AD AC AE ⎛⎫=−=−=− ⎪ ⎪⎝⎭ 设()=x,y,z n 是平面DAE 的法向量,则00AD AE ⎧=⎪⎨=⎪⎩,,n n即01022x z x y z .−+=⎧⎪⎨−++=⎪⎩,可取113=,,⎛⎫ ⎪ ⎪⎝⎭n .设m 是平面AEC 的法向量,则0,0,AC AE ⎧=⎪⎨=⎪⎩m m同理可得(01,=−m . 则77cos ,==n m n m n m . 所以二面角D AE C−−的余弦值为7.【解析】(1)通过题目中的边角关系证明线线垂直,进而得二面角D AC B −−的平面角为DOB ∠,最后利用勾股定理的逆定理得 90DOB ∠=︒,从而得证;(2)根据(1)中得到的垂直关系,建立空间直角坐标系计算即可.20.【答案】解:(1)设()()11222A x ,y ,B x ,y ,l :x my .=+由222x my y x =+⎧⎨=⎩,可得212240则4y my ,y y −−==−.又221212==22y y x ,x ,故()21212==44y y x x . 因此OA 的斜率与OB 的斜率之积为12124==14y y x x −−,所以OA OB ⊥. 故坐标原点O 在圆M 上.(2)由(1)可得()2121212+=2+=++4=24y y m,x x m y y m +.故圆心M 的坐标为()2+2,m m ,圆M 的半径r = 由于圆M 过点42P −(,),因此0AP BP =,故()()()()121244220x x y y −−+++=,即()()121212124+2200x x x x y y y y −++++=由(1)可得1212=-4,=4y y x x ,所以2210m m −−=,解得11或2m m ==−.当1m =时,直线l 的方程为20x y −−=,圆心M 的坐标为(3,1),圆M ,圆M 的方程为()()223110x y −+−=.当12m =−时,直线l 的方程为240x y +−=,圆心M 的坐标为91,-42⎛⎫ ⎪⎝⎭,圆M 的半径为4,圆M 的方程为229185++4216x y ⎛⎫⎛⎫−= ⎪ ⎪⎝⎭⎝⎭. 【解析】(1)设出l 的方程,通过联立方程,证明直线OA 与OB 的斜率之积为1−即可;(2)根据(1)的结论及P 点的坐标即可求解直线与圆的方程.21.【答案】解:(1)()f x 的定义域为()0,+∞.①若0a ≤,因为11=-+2<022f a ln ⎛⎫⎪⎝⎭,所以不满足题意; ②若>0a ,由()1a x a f 'x x x−=−=知,当()0x ,a ∈时,()<0f 'x ;当(),+x a ∈∞时,()>0f 'x ,所以()f x 在()0,a 单调递减,在(),+a ∞单调递增,故x a =是()f x 在()0,+x ∈∞的唯一最小值点. 由于()10f =,所以当且仅当1a =时,()0f x ≥.故1a =.(2)由(1)知当()1,+x ∈∞时,1>0x ln x −−. 令1=1+2n x 得111+<22n n ln ⎛⎫ ⎪⎝⎭,从而 2211111111++1+++1+<+++=1-<12222222n n n ln ln ln ⎛⎫⎛⎫⎛⎫⋅⋅⋅⋅⋅⋅ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 故21111+1+1+<222n e ⎛⎫⎛⎫⎛⎫⋅⋅⋅ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭而231111+1+1+>2222⎛⎫⎛⎫⎛⎫ ⎪⎪⎪⎝⎭⎝⎭⎝⎭,所以m 的最小值为3. 【解析】(1)通过求函数的导数,对函数的单调性进行研究,求解函数最小值点即可;(2)将问题转化为“和”式不等式,根据数列求和公式求解即可.22.【答案】(1)消去参数t 得1l 的普通方程()12l :y k x =−;消去参数m 得2l 的普通方程()212l :y x k=+. 设,P x y (),由题设得()()212y k x y x k ⎧=−⎪⎨=+⎪⎩,消去k 得()2240x y y −=≠. 所以C 的普通方程为()2240x y y −=≠.(2)C 的极坐标方程为()()222cos sin 40<<2ππ−=≠,r q q q q .联立()()222cos sin 4cos +sin ⎧−=⎪⎨⎪⎩r q q r q q 得()cos sin =2cos +sin −q q q q . 故1tan 3=−q ,从而2291cos =,sin =1010q q . 代入()222cos -sin =4r q q 得2=5r ,所以交点M【解析】(1)先将两条直线的参数方程化为普通方程,联立,消去k 即可得所求曲线C 的普通方程;(2)先将(1)中求得的曲线C 的普通方程化为极坐标方程,再与3l 的极坐标方程联立,求出M 的极径即可.23.【答案】解:(1)()31211232,x f x x ,x ,x .−−⎧⎪=−−≤≤⎨⎪⎩<,,> 当<1x −时,()1f x ≥无解; 当12x −≤≤时,由()1f x ≥得,211x −≥,解得12x ≤≤当>2x 时,由()1f x ≥解得>2x .所以()1f x ≥的解集为{}1x x ≥.(2)由()2f x x x m ≥−+得212m x x x x ≤+−−−+,而22212+1+235=+2454x x x x x x x xx ,+−−−+≤−−+⎛⎫−− ⎪⎝⎭≤ 且当32x =时,2512=4x x x x +−−−+. 故m 的取值范围为5-,4⎛⎤∞ ⎥⎝⎦.【解析】(1)直接分段讨论即可解决问题;(2)先分离出参数m ,再将问题转化为最值问题,进而求解参数的取值范围.。


2016年普通高等学校招生全国统一考试理科数学一. 选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)设集合S ={}{}(x 2)(x 3)0,T 0S x x x =--≥=I >P ,则S I T =(A) [2,3] (B)(-∞ ,2]U [3,+∞) (C) [3,+∞) (D)(0,2]U [3,+∞) (2)若z=1+2i ,则41izz =- (A)1 (B) -1 (C) i (D)-i(3)已知向量12(,)22BA =uu v ,31(,),22BC =uu u v 则∠ABC= (A)300(B) 450(C) 600(D)1200(4)某旅游城市为向游客介绍本地的气温情况,绘制了一年中月平均最高气温和平均最低气温的雷达图。
图中A 点表示十月的平均最高气温约为150C ,B 点表示四月的平均最低气温约为50C 。
下面叙述不正确的是(A) 各月的平均最低气温都在00C 以上(B) 七月的平均温差比一月的平均温差大(C) 三月和十一月的平均最高气温基本相同(D) 平均气温高于200C 的月份有5个(5)若3tan 4α=,则2cos 2sin 2αα+= (A)6425 (B) 4825 (C) 1 (D)1625(6)已知432a =,344b =,1325c =,则(A )b a c << (B )a b c <<(C )b c a <<(D )c a b << (7)执行下图的程序框图,如果输入的a =4,b =6,那么输出的n =(A )3 (B )4 (C )5 (D )6(8)在ABC △中,π4B =,BC 边上的高等于13BC ,则cos A = (A )310 (B )10(C )10-(D )310- (9)如图,网格纸上小正方形的边长为1,粗实现画出的是某多面体的三视图,则该多面体的表面积为(A )18365+ (B )54185+(C )90 (D )81(10) 在封闭的直三棱柱ABC -A 1B 1C 1内有一个体积为V 的球,若AB ⊥BC ,AB =6,BC =8,AA 1=3,则V 的最大值是 (A )4π (B )92π(C )6π(D )323π(11)已知O 为坐标原点,F 是椭圆C :22221(0)x y a b a b+=>>的左焦点,A ,B 分别为C 的左,右顶点.P 为C上一点,且PF ⊥x 轴.过点A 的直线l 与线段PF 交于点M ,与y 轴交于点E .若直线BM 经过OE 的中点,则C 的离心率为 (A )13(B )12(C )23(D )34(12)定义“规范01数列”{a n }如下:{a n }共有2m 项,其中m 项为0,m 项为1,且对任意2k m ≤,12,,,k a a a L 中0的个数不少于1的个数.若m =4,则不同的“规范01数列”共有 (A )18个 (B )16个 (C )14个 (D )12个二、填空题:本大题共3小题,每小题5分(13)若x ,y 满足约束条件错误!未找到引用源。

绝密★启用前2017年普通高等学校招生全国统一考试(新课标Ⅲ)理科数学注意事项: 1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A ={}22(,)1x y x y +=│,B ={}(,)x y y x =│,则A B 中元素的个数为 A .3B .2C .1D .02.设复数z 满足(1+i)z =2i ,则∣z ∣=A .12B .2C D .23.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.学#科&网根据该折线图,下列结论错误的是 A .月接待游客量逐月增加 B .年接待游客量逐年增加C .各年的月接待游客量高峰期大致在7,8月份D .各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳 4.(x +y )(2x -y )5的展开式中x 3y 3的系数为 A .-80B .-40C .40D .805.已知双曲线C :22221x y a b-= (a >0,b >0)的一条渐近线方程为y x =,且与椭圆221123x y +=有公共焦点,则C 的方程为 A .221810x y -=B .22145x y -= C .22154x y -= D .22143x y -= 6.设函数f (x )=cos(x +3π),则下列结论错误的是 A .f (x )的一个周期为?2πB .y =f (x )的图像关于直线x =83π对称 C .f (x +π)的一个零点为x =6π D .f (x )在(2π,π)单调递减 7.执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为 A .5B .4C .3D .28.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为 A .πB .3π4C .π2D .π49.等差数列{}n a 的首项为1,公差不为0.若a 2,a 3,a 6成等比数列,则{}n a 前6项的和为 A .-24B .-3C .3D .810.已知椭圆C :22221x y a b+=,(a >b >0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为AB C D .1311.已知函数211()2()x x f x x x a ee --+=-++有唯一零点,则a =A .12-B .13C .12D .112.在矩形ABCD 中,AB=1,AD=2,动点P 在以点C 为圆心且与BD 相切的圆上.若AP =λAB +μAD ,则λ+μ的最大值为A .3B .CD .2二、填空题:本题共4小题,每小题5分,共20分。

数学试卷 第1页(共18页) 数学试卷 第2页(共18页)绝密★启用前2017年普通高等学校招生全国统一考试(全国卷Ⅲ)理科数学一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}22(,)1A x y x y =+=│,{}(,)B x y y x ==│,则A B 中元素的个数( )A.3B.2C.1D.0 2.设复数z 满足()1i z 2i +=,则z =( )A.12D.23.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是( )A.月接待游客量逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7,8月份D.各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳 4.()()5+y 2y x x -的展开式中33y x 的系数为( )A.-80B.-40C.40D.805.已知双曲线2222:1x y C a b-=()00>>a b ,的一条渐近线方程为y x =,且与椭圆221123x y+=有公共焦点,则C 的方程为( ) A.221810x y -= B.22145x y -= C.22154x y -= D.22143x y -= 6.设函数()π3cos ⎛⎫=+ ⎪⎝⎭f x x ,则下列结论错误的是( )A.()f x 的一个周期为2π-B.()f x 的图像关于直线8π=3x 对称 C.()π+f x 的一个零点为π6=x D.()f x 在(π2,π)单调递减 7.执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为( )A.5B.4C.3D.28.已知圆柱的高为1,它的两个底面的圆周在直径2的同一个球的球面上,则该圆柱的体积为( )A.πB.3π4C.π2D.π49.等差数列{}n a 的首项为1,公差不为0.若236a a a ,,成等比数列,则{}n a 前6项的和为 ( ) A.24-B.3-C.3D.810.已知椭圆C :22221x y a b+=()0a b >>的左、右顶点分别为1A ,2A ,且以线段12A A 为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为( )-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________数学试卷 第3页(共18页) 数学试卷 第4页(共18页)D.1311.已知函数211()2(e e )--+=-++x x f x x x a 有唯一零点,则a = ( )A.12-B.13C.12D.112.在矩形ABCD 中,12AB AD ==,,动点P 在以点C 为圆心且与BD 相切的圆上.若AP=AB+AD λμ,则λμ+的最大值为( )A.3D.2二、填空题:本题共4小题,每小题5分,共20分.13.若x ,y 满足约束条件y 0,20,0,x x y y -≥⎧⎪+-≤⎨⎪≥⎩则z 34x y =-的最小值为 .14.设等比数列{}n a 满足1213–1,3a a a a +==--,则4=a . 15.设函数1,0,()2,0,xx x f x x +≤⎧=⎨>⎩则满足1()()12f x f x +->的x 的取值范围是 .16.ab ,为空间中两条互相垂直的直线,等腰直角三角形ABC 的直角边AC 所在直线与a b ,都垂直,斜边AB 以直线AC 为旋转轴旋转,有下列结论:①当直线AB 与a 成60︒角时,AB 与b 成30︒角; ②当直线AB 与a 成60︒角时,AB 与b 成60︒角; ③直线AB 与a 所成角的最小值为45︒; ④直线AB 与a 所成角的最大值为60︒.其中正确的是 .(填写所有正确结论的编号)三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:共60分. 17.(12分)ABC △的内角A B C ,,的对边分别为a b c ,,,已知sin 0=A A,a ,2b =.(1)求c ;(2)设D 为BC 边上一点,且AD AC ⊥,求ABD △的面积.18.(12分)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:(1)求六月份这种酸奶一天的需求量X (单位:瓶)的分布列;(2)设六月份一天销售这种酸奶的利润为Y (单位:元),当六月份这种酸奶一天的进货量n (单位:瓶)为多少时,Y 的数学期望达到最大值?19.(12分)如图,四面体ABCD 中,ABC △是正三角形,ACD △是直角三角形,.ABD CBD AB BD ∠=∠=,(1)证明:平面ACD ⊥平面ABC ;(2)过AC 的平面交BD 于点E ,若平面AEC 把四面体ABCD 分成体积相等的两部分,求二面角––D AE C 的余弦值.数学试卷 第5页(共18页) 数学试卷 第6页(共18页)20.(12分)已知抛物线C :22y x =,过点(2,0)的直线l 交C 与,A B 两点,圆M 是以线段AB 为直径的圆.(1)证明:坐标原点O 在圆M 上;(2)设圆M 过点P (4,-2),求直线l 与圆M 的方程.21.(12分)已知函数1(n )l =--f x a x x . (1)若()0f x ≥,求a 的值;(2)设m 为整数,且对于任意正整数n ,21111+1+1+222n m ⎛⎫⎛⎫⎛⎫⎪⎪⎪⎝⎭⎝⎭⎝⎭<,求m 的最小值.(二)选考题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.22.[选修4-4:坐标系与参数方程](10分)在直角坐标系xOy 中,直线1l 的参数方程为2+,,x t y kt =⎧⎨=⎩(t 为参数),直线2l 的参数方程为2,,x m my k =-+⎧⎪⎨=⎪⎩(m 为参数).设1l 与2l 的交点为P ,当k 变化时,P 的轨迹为曲线C .(1)写出C 的普通方程;(2)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,设3l :()cos si n ρθθ+,M 为3l 与C 的交点,求M 的极径.23.[选修4-5:不等式选讲](10分)已知函数12f x x x =+--(). (1)求不等式1f x ≥()的解集;(2)若不等式2– f x x x m ≥+()的解集非空,求m 的取值范围.2017年普通高等学校招生全国统一考试(全国卷Ⅲ)-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________数学试卷 第7页(共18页) 数学试卷 第8页(共18页)AB 中元素的个数为()1i -,所以3.【答案】A【解析】根据折线图可知,2014年8月到9月、2014年10月到11月等月接待游客量都是减少,所以A 错误. 4.【答案】C【解析】当第一个括号内取x 时,第二个括号内要取含23x y 的项,即()()23352C x y -,当第一个括号内取y 时,第二个括号内要取含32x y 的项,即()()32252C x y -,所以33x y 的系数为()23325522108440C C ⨯-⨯=⨯-=.5.【答案】B【解析】根据双曲线C 的渐近线方程为2y x =,可知2b a = ①,又椭圆221123x y +=的焦点坐标为(3,0)和(3-,0),所以229a b += ②,根据①②可知224,5a b ==,所以选B. 6.【答案】D【解析】根据函数解析式可知函数()f x 的最小正周期为2π ,所以函数的一个周期为π2-,A 正确;当8ππ,3π33=+=x x ,所以πcos 13⎛⎫+=- ⎪⎝⎭x ,所以B 正确;()4cos cos 33ππππ⎛⎫⎛⎫+=++=+ ⎪ ⎪⎝⎭⎝⎭f x x x ,当π6=x 时,4π3π32+=x ,所以()π0+=f x ,所以C 正确;函数()πcos 3⎛⎫=+ ⎪⎝⎭f x x 在(π2,23π)上单调递减;(23π,π)上单调递增,故D 不正确.所以选D . 7.【答案】D【解析】010*******,100911001090,13S M t S M t =+==-==-===,,>;, ,90<91,输出S ,此时,3t =不满足t N ≤,所以输入的正整数N 的最小值为2,故选D. 8.【答案】B【解析】设圆柱的底面半径为r ,则22213=1=24r ⎛⎫-⎪⎝⎭,所以,圆柱的体积33=π1=π44⨯V ,故选B. 9.【答案】A【解析】设等差数列n a 的公差为d ,因为236,,a a a 成等比数列,所以2263a a a =,即()()()211152a d a d a d ++=+,又11a =,所以220d d +=,又0,d ≠则2d =-,所以6159a a d =+=-,所以n a 的前6项的和6196242S -=⨯=-,故选A. 10.【答案】A以线段12A A 为直径的圆的方程为222x y a +=,由原点到直线20bx ay ab -+=的距离==d a ,得223a b =,所以C 的离心率3e ==.11.【答案】C【解析】由()()2112x x f x x x a e e --+=-++,得()()()()()(221212112122224422x x x x x f x x x a e e x x x a e e x x a e --+-----⎡⎤-=---++=-++++=-+⎣⎦,所以()()2f x f x -=,即1x =为()f x 图像的对称轴.由题意()f x 有唯一零点,所以()f x 的零点只能为1x =,即()()2111111210f a e e --+=-⨯++=,解得12a =.故选C. 12.【答案】A【解析】以A 为坐标原点,AB AD ,所在直线分别为x ,y 轴建立如图所示的平面直角坐标系,则A (0,0),B (1,0),C (1,2),D (0,2),可得直线BD 的方程为220x y +-=,点C 到直线BD =,圆C :数学试卷 第9页(共18页) 数学试卷 第10页(共18页)()()224125x y -+-=,因为P 在圆C 上,所以P(1cos 5θ+,25θ+)(1,0)AB =,(0,2)AD =,(,2)AP AB AD λμλμ=+=,所以122{θλθμ==()22sin 3λμθθθα+==++≤,tan 2α=,选A.13.【答案】1-【解析】作出约束条件表示的可行域如图中阴影部分所示,作出直线:340l x y -=,平移直线l ,当直线34z x y =-经过点A (1,1)时,z 取得最小值,最小值为341-=-.14.【答案】8-【解析】设等比数列{}n a 的公比为q ,则121(1)1a a a q +=+=-,2131(1)3a a a q -=-=-,两式相除,得21113q q +=-,解得12,1q a =-=,所以3418a a q ==-.15.【答案】∞1(-,+)4【解析】当0x >,()=21xf x >恒成立,当102x ->,即12x >时,121()=212x f x -->,当102x -≤,即102x ≤<时,111()=222f x x -+>,则不等式1()()12f x f x +->恒成立.当0x ≤时,113()()121222+-=+++=+f x f x x x x >,所以104x -≤<.综上所述,x 的取值范围是(14-,+∞).16.【答案】②③【解析】由题意知,,,a b AC 三条直线两两相互垂直,画出图形如图.不妨设图中所示正方体的棱长为1,则1,AC AB ==AB 以直线AC 为旋转轴旋转,则A点保持不变,B 点的运动轨迹是以C 为圆心,l 为半径的圆.数学试卷 第11页(共18页) 数学试卷 第12页(共18页)以C 为坐标原点,以CD 的方向为x 轴正方向,CB 方向为y 轴正方向,CA 的方向为z 轴正方向建立空间直角坐标系.则D (1,0,0),A (0,0,1), 直线a 的单位方向向量(0,1,0), 1.a a == B 点起始坐标为(0,1,0), 直线b 的单位方向向量b (1,0,0), 1.b == 设B 点在运动过程中的坐标B'(cos ,sin ,0)θθ, 其中θ为'CB 与CD 的夹角,[0,2)θπ∈.那么AB'在运动过程中的向量'(cos ,sin ,1),'2AB AB θθ=-=.设直线AB'与a 所成的夹角为[0,2],απ∈(cos ,sin ,1)(0,1,0)cos a ABθθαθ-⋅==∈ 故[,],42ππα∈所以③正确,④错误. 设直线AB'与b 所成的夹角为β,则[0,2],βπ∈'b cos 'AB b AB β⋅=(cos ,sin ,1)(1,0,0)'b AB θθ-⋅=.θ 当'AB 与a 成60︒角时,=3πα,1sin=322πθα因为22sin+cos =1,θθ所以cos =2θ 所以1cos =.2βθ 因为[0,2],βπ∈所以=3πβ,此时'AB 与b 成60︒角.所以②正确,①错误.三、解答题17.【答案】解:(1)由已知得tan =A 所以2π3A=. 在ABC 中,由余弦定理得22π2844cos3=+-c c ,即2+224=0c c -. 解得c 6=-,(舍去),c =4(2)由题设可得π=2∠CAD ,所以π6∠=∠-∠=BAD BAC CAD .故ABD 面积与ACD 面积的比值为1πsin 26112AB AD AC AD= 又ABC 的面积为142sin 2BAC ⨯⨯∠=所以ABD ∆【解析】(1))先求出角A ,再根据余弦定理求出c 即可;(2)根据ABD ,ACD ,ABC 的面积之间的关系求解即可.18.【答案】解:(1)由题意知,X所有的可能取值为200,300,500,由表格数据知()2162000.290P X +===,数学试卷 第13页(共18页) 数学试卷 第14页(共18页)()363000.490P X ===,()25745000.490P X ++===. 因此X 的分布列为(2200,因此只需考虑200500n ≤≤当300500n ≤≤时,若最高气温不低于25,则642Y n n n =-=;若最高气温位于区间[)20,,25,则63002300412002;Y n n n =⨯+--=-() 若最高气温低于20,则6200220048002;Y n n n =⨯+--=-() 因此()20.4120020.480020.26400.4.EY n n n n =⨯+-⨯+-⨯=-() 当200300n <≤时,若最高气温不低于20,则642;Y n n n =-=若最高气温低于20,则6200220048002;Y n n n =⨯+--=-() 因此()()20.40.480020.2160 1.2.EY n n n =⨯++-⨯=+ 所以300n =时,Y 的数学期望达到最大值,最大值为520元.【解析】(1)根据表格提供的数据进行分类求解即可;(2)根据分布列得到关于利润的函数表达式,进而求解最值. 19.解:(1)由题设可得,,ABD CBD ∆≅∆从而AD DC =. 又ACD ∆是直角三角形,所以0=90ACD ∠.取AC 的中点O ,连接,,DO BO 则,.DO AC DO AO ⊥= 又由于ABC ∆是正三角形,故BO AC ⊥. 所以DOB ∠为二面角D AC B --的平面角. 在Rt AOB ∆中,222BO AO AB +=.又AB BD =,所以222222BO DO BO AO AB BD +=+==,故0∠DOB=90.所以平面ACD ⊥平面ABC .(2)由题设及(1)知,OA,OB,OD 两两垂直,以O 为坐标原点,OA 的方向为x 轴正方向,OA为单位长,建立如图所示的空间直角坐标系O xyz -,则-(1,0,0),(0(1,0,0),(0,0,1)A B C D .由题设知,四面体ABCE 的体积为四面体ABCD 的体积的12,从而E 到平面ABC 的距离为D 到平面ABC 的距离的12,即E 为DB 的中点,得102E ⎛⎫ ⎪ ⎪⎝⎭,,故()()11,0,1,2,0,0,1,2AD AC AE ⎛⎫=-=-=- ⎪ ⎪⎝⎭设()=x,y,z n 是平面DAE 的法向量,则0AD AE ⎧=⎪⎨=⎪⎩,,n n即01022x z x y z .-+=⎧⎪⎨-++=⎪⎩,可取113=,⎛⎫⎪ ⎪⎝⎭n .设m 是平面AEC 的法向量,则0,0,AC AE ⎧=⎪⎨=⎪⎩m m 同理可得(01,=-m .则77cos ,==n m n m n m . 所以二面角D AE C --.数学试卷 第15页(共18页) 数学试卷 第16页(共18页)【解析】(1)通过题目中的边角关系证明线线垂直,进而得二面角D AC B --的平面角为DOB ∠,最后利用勾股定理的逆定理得 90DOB ∠=︒,从而得证;(2)根据(1)中得到的垂直关系,建立空间直角坐标系计算即可. 20.【答案】解:(1)设()()11222A x ,y ,B x ,y ,l :x my .=+ 由222x my y x=+⎧⎨=⎩,可得212240则4y my ,y y --==-.又221212==22y y x ,x ,故()21212==44y y x x . 因此OA 的斜率与OB 的斜率之积为12124==14y y x x --,所以OA OB ⊥. 故坐标原点O 在圆M 上.(2)由(1)可得()2121212+=2+=++4=24y y m,x x m y y m +. 故圆心M 的坐标为()2+2,m m ,圆M 的半径r =由于圆M 过点42P -(,),因此0AP BP = ,故()()()()121244220x x y y --+++=,即()()121212124+2200x x x x y y y y -++++= 由(1)可得1212=-4,=4y y x x , 所以2210m m --=,解得11或2m m ==-. 当1m =时,直线l 的方程为20x y --=,圆心M 的坐标为(3,1),圆M 的半径为,圆M 的方程为()()223110x y -+-=.当12m =-时,直线l 的方程为240x y +-=,圆心M 的坐标为91,-42⎛⎫⎪⎝⎭,圆M 的半径为4,圆M 的方程为229185++4216x y ⎛⎫⎛⎫-= ⎪ ⎪⎝⎭⎝⎭.【解析】(1)设出l 的方程,通过联立方程,证明直线OA 与OB 的斜率之积为1-即可; (2)根据(1)的结论及P 点的坐标即可求解直线与圆的方程. 21.【答案】解:(1)()f x 的定义域为()0,+∞.①若0a ≤,因为11=-+2<022f a ln ⎛⎫⎪⎝⎭,所以不满足题意; ②若>0a ,由()1a x a f 'x x x-=-=知,当()0x ,a ∈时,()<0f 'x ;当(),+x a ∈∞时,()>0f 'x ,所以()f x 在()0,a 单调递减,在(),+a ∞单调递增,故x a =是()f x 在()0,+x ∈∞的唯一最小值点.由于()10f =,所以当且仅当1a =时,()0f x ≥. 故1a =.(2)由(1)知当()1,+x ∈∞时,1>0x ln x --. 令1=1+2n x 得111+<22n n ln ⎛⎫ ⎪⎝⎭,从而 2211111111++1+++1+<+++=1-<12222222n n n ln ln ln ⎛⎫⎛⎫⎛⎫⋅⋅⋅⋅⋅⋅ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭故21111+1+1+<222n e ⎛⎫⎛⎫⎛⎫⋅⋅⋅ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭而231111+1+1+>2222⎛⎫⎛⎫⎛⎫⎪⎪⎪⎝⎭⎝⎭⎝⎭,所以m 的最小值为3. 【解析】(1)通过求函数的导数,对函数的单调性进行研究,求解函数最小值点即可;(2)将问题转化为“和”式不等式,根据数列求和公式求解即可.数学试卷 第17页(共18页) 数学试卷 第18页(共18页)22.【答案】(1)消去参数t 得1l 的普通方程()12l :y k x =-;消去参数m 得2l 的普通方程()212l :y x k=+.设,P x y (),由题设得()()212y k x y x k ⎧=-⎪⎨=+⎪⎩,消去k 得()2240x y y -=≠. 所以C 的普通方程为()2240x y y -=≠. (2)C 的极坐标方程为()()222cossin 40<<2ππ-=≠,.联立()()222cossin 4cos +sin-2=0⎧-=⎪⎨⎪⎩得()cossin =2cos +sin -.故1tan 3=-,从而2291cos =,sin =1010.代入()222cos-sin =4得2=5,所以交点M .【解析】(1)先将两条直线的参数方程化为普通方程,联立,消去k 即可得所求曲线C的普通方程;(2)先将(1)中求得的曲线C 的普通方程化为极坐标方程,再与3l 的极坐标方程联立,求出M 的极径即可.23.【答案】解:(1)()31211232,x f x x ,x ,x .--⎧⎪=--≤≤⎨⎪⎩<,,> 当<1x -时,()1f x ≥无解;当12x -≤≤时,由()1f x ≥得,211x -≥,解得12x ≤≤ 当>2x 时,由()1f x ≥解得>2x . 所以()1f x ≥的解集为{}1x x ≥.(2)由()2f x x x m ≥-+得212m x x x x ≤+---+,而22212+1+235=+2454x x x x x x x xx ,+---+≤--+⎛⎫-- ⎪⎝⎭≤且当32x =时,2512=4x x x x +---+. 故m 的取值范围为5-,4⎛⎤∞ ⎥⎝⎦.【解析】(1)直接分段讨论即可解决问题;(2)先分离出参数m ,再将问题转化为最值问题,进而求解参数的取值范围.。
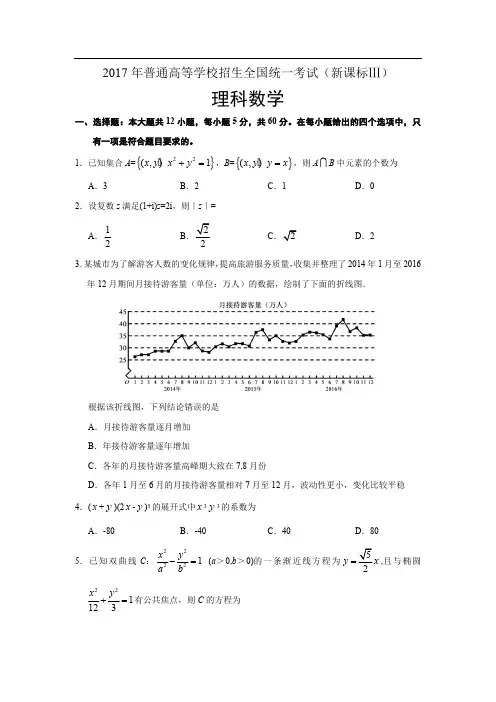
2017年普通高等学校招生全国统一考试(新课标Ⅲ)理科数学一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A =,B =,则A B 中元素的个数为{}22(,)1x y x y +=│{}(,)x y y x =│ A .3B .2C .1D .02.设复数z 满足(1+i)z =2i ,则∣z ∣=A .B C D .2123.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是A .月接待游客量逐月增加B .年接待游客量逐年增加C .各年的月接待游客量高峰期大致在7,8月份D .各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳4.(+)(2-)5的展开式中33的系数为x y x y x y A .-80B .-40C .40D .805.已知双曲线C : (a >0,b >0)的一条渐近线方程为,且与椭圆22221x y a b -=y x =有公共焦点,则C 的方程为221123x y +=A .B .C .D .221810x y -=22145x y -=22154x y -=22143x y -=6.设函数f (x )=cos(x +),则下列结论错误的是3πA .f (x )的一个周期为−2πB .y =f (x )的图像关于直线x =对称83πC .f (x +π)的一个零点为x =D .f (x )在(,π)单调递减6π2π7.执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为A .5B .4C .3D .28.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为A .B .C .D .π3π4π2π49.等差数列的首项为1,公差不为0.若a 2,a 3,a 6成等比数列,则前6项的和{}n a {}n a 为A .-24B .-3C .3D .810.已知椭圆C :,(a >b >0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为22221x y a b+=直径的圆与直线相切,则C 的离心率为20bx ay ab -+=A B C D .1311.已知函数有唯一零点,则a =211()2()x x f x x x a e e --+=-++A .B .C .D .112-131212.在矩形ABCD 中,AB=1,AD=2,动点P 在以点C 为圆心且与BD 相切的圆上.若=AP+,则+的最大值为λAB μADλμA .3B.CD .2二、填空题:本题共4小题,每小题5分,共20分。

绝密★启用前2017年普通高等学校招生全国统一考试(全国Ⅲ卷)理科数学参考答案一、选择题1.B2.C3.A4.C5.B6.D7.D8.B9.A 10.A 11.C 12.A 二、填空题13. -1 14. -8 15.∞1(-,+)416. ②③ 三、解答题 17.解:(1)由已知得tanA=π2A=3在 △ABC 中,由余弦定理得2222844cos+2-24=03c 6c c c c c π=+-=-,即解得(舍去),=4 (2)有题设可得ππ∠∠=∠-∠==,所以26CAD BAD BAC CAD故△ABD 面积与△ACD 面积的比值为π=g g g 1sin 26112AB AD AC AD 又△ABC的面积为⨯⨯∠=∆142sin 2BAC ABD18.解:(1)由题意知,X 所有的可能取值为200,300,500,由表格数据知()2162000.290P X +=== ()363000.490P X ===()25745000.490P X ++===.因此X 的分布列为,因此只需考虑200500n ≤≤ 当300500n ≤≤时,若最高气温不低于25,则Y=6n-4n=2n若最高气温位于区间[)20,,25,则Y=6×300+2(n-300)-4n=1200-2n; 若最高气温低于20,则Y=6×200+2(n-200)-4n=800-2n; 因此EY=2n ×0.4+(1200-2n )×0.4+(800-2n) ×0.2=640-0.4n 当200300n <≤时,若最高气温不低于20,则Y=6n-4n=2n;若最高气温低于20,则Y=6×200+2(n-200)-4n=800-2n; 因此EY=2n ×(0.4+0.4)+(800-2n)×0.2=160+1.2n 所以n=300时,Y 的数学期望达到最大值,最大值为520元。
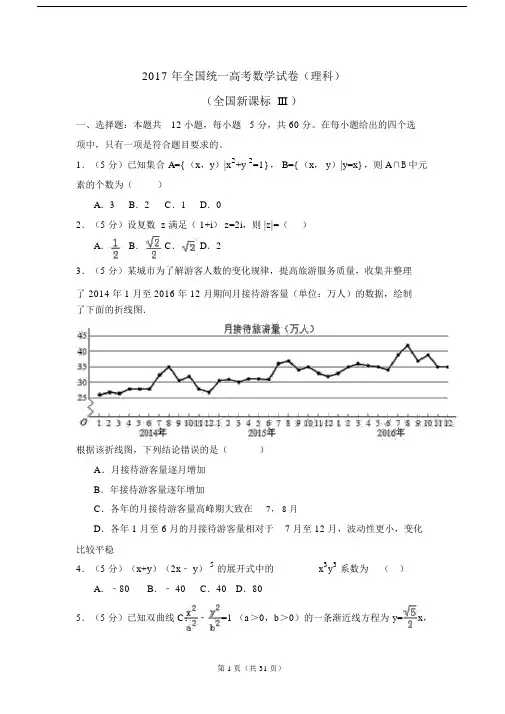
2017 年全国统一高考数学试卷(理科)(全国新课标III )一、选择题:本题共12 小题,每小题 5 分,共 60 分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5 分)已知集合 A={ (x,y)|x2+y 2=1} , B={ (x, y)|y=x} ,则 A∩B中元素的个数为()A.3 B.2 C.1 D.02.(5 分)设复数 z 满足( 1+i) z=2i,则 |z|=()A.B.C.D.23.(5 分)某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014 年 1 月至 2016 年 12 月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是()A.月接待游客量逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7, 8 月D.各年 1 月至 6 月的月接待游客量相对于7 月至 12 月,波动性更小,变化比较平稳4.(5 分)(x+y)(2x﹣ y)5的展开式中的x3y3系数为()A.﹣80B.﹣ 40C.40 D.805.(5 分)已知双曲线 C:﹣=1 (a>0,b>0)的一条渐近线方程为 y=x,且与椭圆+ =1 有公共焦点,则 C 的方程为()A.﹣=1B.﹣=1C.﹣=1D.﹣=16.(5 分)设函数 f( x) =cos(x+),则下列结论错误的是()A .f( x)的一个周期为﹣ 2πB. y=f (x)的图象关于直线x=对称C. f( x+π)的一个零点为x=D.f( x)在(,π)单调递减7.(5 分)执行如图的程序框图,为使输出S 的值小于 91,则输入的正整数N 的最小值为()A.5 B.4 C.3 D.28.(5 分)已知圆柱的高为1,它的两个底面的圆周在直径为 2 的同一个球的球面上,则该圆柱的体积为()A .πB.C.D.9.(5 分)等差数列 {a n} 的首项为 1,公差不为 0.若 a2,a3,a6成等比数列,则{a n} 前 6 项的和为()A.﹣24B.﹣ 3 C.3 D.810.( 5 分)已知椭圆C:=1(a>b>0)的左、右顶点分别为 A 1,A 2,且以线段 A 1A 2为直径的圆与直线 bx﹣ay+2ab=0 相切,则 C 的离心率为()A.B.C.D.11.( 5 分)已知函数2x﹣ 1﹣ x+1)有唯一零点,则 a=()f(x)=x ﹣ 2x+a(e+eA .﹣B.C.D.112.( 5 分)在矩形 ABCD 中, AB=1 , AD=2 ,动点 P 在以点 C 为圆心且与 BD 相切的圆上.若=λ +μ,则λ+μ的最大值为()A.3 B.2 C.D.2二、填空题 :本题共 4 小题,每小题 5 分,共 20 分。
2017 年普通高等学校招生全国统一考试(新课标Ⅲ)理科数学一、选择题:本大题共12 小题,每小题 5 分,共 60 分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合 A= (x,y│) x2y 21 ,B= ( x,y│) y x ,则 A B 中元素的个数为A .3 B.2C. 1 D. 02.设复数 z满足 (1+i) z=2i ,则∣ z∣ =1B.2C. 2 D. 2A .2 23.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014 年 1 月至2016 年 12 月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是A.月接待游客量逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7,8 月份D .各年 1 月至 6 月的月接待游客量相对7 月至 12 月,波动性更小,变化比较平稳4. ( x+ y )(2 x - y )5的展开式中 x 3y 3的系数为A .-80B. -40 C. 40 D. 80x2y21(a > 0,b > 0) 的一条渐近线方程为y 5 x , 且与椭圆5 .已知双曲线C:b2a2 2x2y21有公共焦点,则 C 的方程为12 3x2y 2B.x2y2C.x2y 2x2y 2A . 14 151 D. 18 10 5 4 4 36.设函数f(x)=cos(x+),则下列结论错误的是3A .f(x)的一个周期为 -2 πB . y=f(x)的图像关于直线x= 8对称3C. f(x+π)的一个零点为x=D .f(x)在(, π)单调递减6 27.执行下面的程序框图,为使输出S 的值小于91,则输入的正整数 N 的最小值为A .5B . 4C. 3 D. 28.已知圆柱的高为1,它的两个底面的圆周在直径为 2 的同一个球的球面上,则该圆柱的体积为A .πB.3πππ4C.D.2 49.等差数列 a n的首项为 1,公差不为0.若 a2, a3, a6成等比数列,则a n前 6 项的和为A .-24B . -3C. 3 D. 8x2y21,( a>b>0)的左、右顶点分别为A1, A2,且以线段A1A2 为10.已知椭圆 C:b2a2直径的圆与直线bx ay 2ab 0 相切,则 C 的离心率为6 3C.2 1A .B.3 D.3 3 311.已知函数 f ( x) x22x a(e x 1 e x 1 ) 有唯一零点,则 a=A . 1B . 1C . 1D . 12 3 2 12.在矩形 ABCD 中,AB=1 ,AD=2 ,动点 P 在以点 C 为圆心且与BD 相切的圆上. 若 AP = AB + AD ,则 + 的最大值为A .3B . 2 2C . 5D . 2二、填空题:本题共 4 小题,每小题 5 分,共 20分。
x y 0 3x 4 y 的最小值为 __________ ..若 x , y 满足约束条件 x y 2 0 ,则 z 13y 014.设等比数列 a n 满足 a1 + a2 = –1, a1–a3 = –3,则 a4 = ___________.x , , 11 x 0 f( x 1 的 x 的取值围是 _________。
15.设函数 f (x) x , x , 则满足f ( x) ) 2 0 216. a ,b 为空间中两条互相垂直的直线,等腰直角三角形ABC 的直角边 AC 所在直线与 a , b 都垂直,斜边 AB 以直线 AC 为旋转轴旋转,有下列结论:①当直线 AB 与 a 成 60°角时, AB 与 b 成30°角;②当直线 AB 与 a 成 60°角时, AB 与 b 成60°角;③直线 AB 与 a 所成角的最小值为 45°;④直线 AB 与 a 所成角的最小值为 60°;其中正确的是 ________。
(填写所有正确结论的编号)三、解答题:共 70 分。
解答应写出文字说明、证明过程或演算步骤。
第 17~21 题为必考题,每个试题考生都必须作答。
第 22、 23 题为选考题,考生根据要求作答。
(一)必考题:共 60 分。
17.( 12 分)△ABC 的角A ,B ,C的对边分别为a ,b ,c ,已知sinA +3 cosA=0,a=27 ,b=2.( 1)求 c ;( 2)设 D 为 BC 边上一点, 且 AD AC,求 △ABD 的面积.18.( 12 分)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4 元,售价每瓶 6 元,未售出的酸奶降价处理, 以每瓶 2 元的价格当天全部处理完. 根据往年销售经验, 每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500 瓶;如果最高气温位于区间 [20 , 25),需求量为300 瓶;如果最高气温低于20,需求量为200 瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:最高气温[10, 15)[15,20)[20 , 25)[25, 30)[30, 35)[35 ,40)天数 2 16 36 25 7 4 以最高气温位于各区间的频率代替最高气温位于该区间的概率。
(1)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列;(2)设六月份一天销售这种酸奶的利润为 Y(单位:元),当六月份这种酸奶一天的进货量 n(单位:瓶)为多少时, Y 的数学期望达到最大值?19.( 12 分)如图,四面体 ABCD 中,△ABC 是正三角形,△ACD 是直角三角形,∠ ABD =∠ CBD ,AB=BD .(1)证明:平面 ACD ⊥平面 ABC;(2)过 AC 的平面交 BD 于点 E,若平面 AEC 把四面体 ABCD 分成体积相等的两部分,求二面角 D –AE–C 的余弦值.20.( 12 分)已知抛物线 C: y2=2 x,过点( 2,0)的直线 l 交 C 与 A,B 两点,圆 M 是以线段 AB 为直径的圆.( 1)证明:坐标原点 O 在圆 M上;(2)设圆 M 过点 P(4, -2),求直线 l 与圆 M 的方程.21.( 12 分)已知函数 f ( x) =x﹣ 1﹣ alnx.( 1)若 f (x) 0,求 a 的值;( 2)设 m 为整数,且对于任意正整数n,(1+ 1)(1 +1) (1+1) ﹤ m,求 m 的最小2 222n值.(二)选考题:共 10 分。
请考生在第 22、23 题中任选一题作答,如果多做,则按所做的第一题计分。
22. [选修4 - 4:坐标系与参数方程] ( 10分)在直角坐标系 xOy 中,直线 l1的参数方程为x 2+t ,( t 为参数),直线 l2的参数方程y kt, x 2 m,为(为参数).设 l1与 l2的交点为 P,当 k 变化时, P 的轨迹为曲线 C.y m ,mk( 1)写出 C 的普通方程;( 2)以坐标原点为极点, x 轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ)-2=0,M 为 l 3与 C 的交点,求 M 的极径.23. [选修4 - 5:不等式选讲 ]( 10 分)已知函数 f( x)=│x+1│–│x–2│.(1)求不等式 f( x)≥1的解集;(2)若不等式 f( x)≥x2–x +m 的解集非空,求 m 的取值围.绝密★启用前2017 年普通高等学校招生全国统一考试理科数学试题正式答案一、选择题1.B2.C3.A4.C5.B6.D7.D 8.B 9.A 10.A 11.C 12.A二、填空题13. -1 14. -8 15. (-1,+)16.②③4三、解答题17.解:(1)由已知得tanA= 3,所以 A= 23在△ ABC中,由余弦定理得28 4 c24c cos 2 ,即 c2 +2c-24=03解得c (舍去),c=4 6(2)有题设可得CAD =,所以BAD BAC CAD2 61AB ADsin故△ ABD面积与△ ACD面积的比值为21 AC AD 6121 42 sinBAC 2 3,所以的面积为3.又△ ABC的面积为ABD218. 解:(1)由题意知,X 所有的可能取值为200,300,500 ,由表格数据知P X 200 2 160.290P X 300 360.4 90P X 500 25 7 4 0.4.90因此X的分布列为X 200300 500P 0.2 0.4 0.4⑵由题意知,这种酸奶一天的需求量至多为500,至少为 200,因此只需考虑 200 ≤ n ≤500当300 ≤ n ≤ 500 时,若最高气温不低于 25,则 Y=6n-4n=2n若最高气温位于区间20, ,25,则 Y=6× 300+2( n-300 ) -4n=1200-2n;若最高气温低于20 ,则 Y=6×200+2( n-200 ) -4n=800-2n; 因此 EY=2n× 0.4+ ( 1200-2n )×0.4+(800-2n)× 0.2=640-0.4n 当 200 ≤ n 300 时,若最高气温不低于 20,则 Y=6n-4n=2n;若最高气温低于20 ,则 Y=6×200+2( n-200 ) -4n=800-2n; 因此 EY=2n× (0.4+0.4)+(800-2n) ×0.2=160+1.2n所以 n=300时, Y的数学期望达到最大值,最大值为520元。
19. 解:(1)由题设可得,ABD CBD , 从而 AD DC又 ACD 是直角三角形,所以ACD =90 0取AC的中点 O,连接 DO,BO,则DO⊥ AC,DO=AO 又由于ABC是正三角形,故BO AC所以 DOB 为二面角 DAC B 的平面角在 中, BO 2AO 2 AB 2 Rt AOB 又 AB BD ,所以BO 2 DO 2 BO 2 AO 2 AB 2 2 ,故 0 BD DOB=90所以平面 ACD 平面 ABC (2)由题设及( 1)知,OA, OB, OD 两两垂直,以 O 为坐标原点, OA 的方向为 x 轴正方向,OA为单位长,建立如图所示的空间直角坐标系O - xyz,则(1,0,0), (0,3,0), ( 1,0,0), (0,0,1)ABCD由题设知,四面体 ABCE 的体积为四面体ABCD 的体积的 1 ,从而 E 到平面 ABC 的距离 2 1 ,即 E 为 DB 的中点,得 E 0,3 1 .故为 D 到平面 ABC 的距离的 , 2 2 2 1,0,1 , 2,0,0 ,3 1AD 1, , AC AE 2 2n AD0, x z 0设 n = x,y,z 是平面 DAE 的法向量,则 31 n AE 即x y 0 0,2 z2 可取 n = 1, 3,13m AC0,设 m 是平面 AEC 的法向量,则同理可得 m 0, 1, 3 m AE 0,n m7 则 cos n,m7 n m7 所以二面角 D-AE-C 的余弦值为720.解(1)设 A x 1 ,y 1 ,Bx 2 ,y 2,l : x my2 xmy 22my 4 0,则 y 1 y 2 4由2 2x 可得 y 2y 2 2y 1 y 2 2又 x 1 = y1,x 2 = y2=4,故x 1x 2 =2 2 4 因此 OA 的斜率与 OB 的斜率之积为 y 1 y2 = -4=-1x 1 x 2 4所以 OA ⊥ OB故坐标原点 O 在圆 M 上 .(2)由( 1)可得 y 1 +y 2 =2m,x 1 +x 2 =m y 1 +y 2 +4=2m 24故圆心 M 的坐标为m 2+2, m ,圆 M 的半径 r m 22 m 22由于圆 M 过点 P ( 4,-2),因此 AP BP 0 ,故 x 1 4 x 2 4 y 1 2 y 2 2即 x 1 x 24 x 1 +x 2 y 1 y 2 2 y 1 y 220 0由( 1)可得 y 1 y 2 =-4,x 1x 2 =4 ,所以 2m 2m 1 0 ,解得m 1或m 12 .当 m=1 时,直线 l 的方程为 x-y-2=0 ,圆心 M 的坐标为( 3,1),圆 M 的半径为 10 ,圆 Mx 2 y2 10的方程为3 11 时,直线 l 的方程为2x 9 1 当 my 4 0 ,圆心 M 的坐标为 ,-2 4 2,圆 M 的半径为8522x 9 + y+ 185 ,圆 M 的方程为4 4 2 1621.解:( 1) f x 的定义域为0,+ .①若 a 0 ,因为f1 =- 1+aln 2<0 ,所以不满足题意;2 2②若 a > 0,由 f ' x 1 a x a 0,a 时, f 'x <0 ;当 x a ,+ 时, x 知,当 x x f ' x >0 ,所以 f x 在 0,a 单调递减,在 a ,+ 单调递增,故 x=a 是 f x 在x0,+ 的唯一最小值点 .由于 f 1 0 ,所以当且仅当 a=1 时, f x 0 .故 a=1(2)由( 1)知当 x 1,+时, x 1 ln x >0 令 =1+ 1得 ln 1+ 1< 1,从而 x 2n 2n 2nln 1+ 1+ ln 1+ 1+ + ln 1+ 1< 1+ 1+ + 1=1- 1<12222n2 222n2n故 1+ 1 1+ 11+1 < e2 22 2n而 1+11+ 11+ 1>2 ,所以 m 的最小值为 3.2 222322.解:( 1 )消去参数 t 得 l 1 的普通方程 l 1 : y k x 2 ;消去参数 m 得 l 2 的普通方程 l 2 :y 1 x 2k y k x2设 P ( x,y ),由题设得 y 1 x ,消去 k 得 x 2 y 24 y 0 . 2k所以 C 的普通方程为 x 2y 24 y 0 (2) C 的极坐标方程为r2 cos 2q sin 2q 4 0< q <2pq,pr 2 cos2q sin2q 4sinq =2 cosq + sinq联立得 cosq .r cosq + sinq - 2=0故tanq 1 2 = 9, 2 = 1 3,从而 cos q 10 sin q 10代入 r2cos2q - sin2q =4得r 2 =5,所以交点 M 的极径为5 .23.解:3, x< 1 (1) f x2x 1, 1 x 23, x>2当 x<1时,fx 1无解;当 1 x 2 时,由f x 1得, 2x 1 1,解得 1 x 2当 x>2 时,由 f x 1 解得 x>2 .所以f x 1的解集为x x 1.(2)由 f xx2x m 得 m x 1 x 2 x2x ,而x 1 x 2 x2x x +1+ x 2 x2x=-3 25 x - +4254且当 x 3 时, x 1 x 2 x2x = 5 .2 4故 m 的取值围为-5 ,4。