数据结构课程设计树与二叉树的转换
- 格式:doc
- 大小:266.50 KB
- 文档页数:13

数据结构有序树转⼆叉树(树的遍历)Description计算输⼊有序树的深度和有序树转化为⼆叉树之后树的深度。
Input输⼊包含多组数据。
每组数据第⼀⾏为⼀个整数n(2<=n<=30000)代表节点的数量,接下来n-1⾏,两个整数a、b代表a是b的⽗亲结点。
Output输出当前树的深度和转化成⼆叉树之后的深度。
Sample Input51 51 35 21 4Sample Output3 4HINTAppend Code析:这个题很好说,只要遍历⼀次就能得到答案,由于要先有序树转成⼆叉树,我也没听过,我百度了⼀下怎么转,看到百度百科中有,我总结⼀下就是,左⼉⼦,右兄弟,和那个字典树有的⼀拼,也就是左结点是⼉⼦结点,⽽右结点是兄弟结点,那么我们可以⽤两个参数来记录深度,⼆叉树既然是右兄弟,那么同⼀深度的就会多⼀层,加1,这样最⼤的就是答案。
代码如下:#pragma comment(linker, "/STACK:1024000000,1024000000")#include <cstdio>#include <string>#include <cstdlib>#include <cmath>#include <iostream>#include <cstring>#include <set>#include <queue>#include <algorithm>#include <vector>#include <map>#include <cctype>#include <cmath>#include <stack>#define debug puts("+++++")//#include <tr1/unordered_map>#define freopenr freopen("in.txt", "r", stdin)#define freopenw freopen("out.txt", "w", stdout)using namespace std;//using namespace std :: tr1;typedef long long LL;typedef pair<int, int> P;const int INF = 0x3f3f3f3f;const double inf = 0x3f3f3f3f3f3f;const LL LNF = 0x3f3f3f3f3f3f;const double PI = acos(-1.0);const double eps = 1e-8;const int maxn = 3e4 + 5;const LL mod = 1e3 + 7;const int N = 1e6 + 5;const int dr[] = {-1, 0, 1, 0, 1, 1, -1, -1};const int dc[] = {0, 1, 0, -1, 1, -1, 1, -1};const char *Hex[] = {"0000", "0001", "0010", "0011", "0100", "0101", "0110", "0111", "1000", "1001", "1010", "1011", "1100", "1101", "1110", "1111"}; inline LL gcd(LL a, LL b){ return b == 0 ? a : gcd(b, a%b); }inline int gcd(int a, int b){ return b == 0 ? a : gcd(b, a%b); }inline int lcm(int a, int b){ return a * b / gcd(a, b); }int n, m;const int mon[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};const int monn[] = {0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};inline int Min(int a, int b){ return a < b ? a : b; }inline int Max(int a, int b){ return a > b ? a : b; }inline LL Min(LL a, LL b){ return a < b ? a : b; }inline LL Max(LL a, LL b){ return a > b ? a : b; }inline bool is_in(int r, int c){return r >= 0 && r < n && c >= 0 && c < m;}vector<int> G[maxn];bool in[maxn];int ans1, ans2;void dfs(int u, int cnt1, int cnt2){ans1 = Max(ans1, cnt1);ans2 = Max(ans2, cnt2);for(int i = 0; i < G[u].size(); ++i)dfs(G[u][i], cnt1+1, cnt2+i+1);}int main(){while(scanf("%d", &n) == 1){for(int i = 0; i <= n; ++i) G[i].clear(), in[i] = 0;int u, v;for(int i = 1; i < n; ++i){scanf("%d %d", &u, &v);G[u].push_back(v);in[v] = true;}ans1 = ans2 = 0;for(int i = 1; i <= n; ++i) if(!in[i]){dfs(i, 1, 1); break;}printf("%d %d\n", ans1, ans2);}return 0;}。

二叉树,树,森林遍历之间的对应关系一、引言在计算机科学中,数据结构是非常重要的知识点之一。
而树这一数据结构,作为基础的数据结构之一,在软件开发中有着广泛的应用。
本文将重点探讨二叉树、树和森林遍历之间的对应关系,帮助读者更加全面地理解这些概念。
二、二叉树1. 二叉树的定义二叉树是一种特殊的树结构,每个节点最多有两个子节点,分别称为左子节点和右子节点。
二叉树可以为空,也可以是一棵空树。
2. 二叉树的遍历在二叉树中,有三种常见的遍历方式,分别是前序遍历、中序遍历和后序遍历。
在前序遍历中,节点的访问顺序是根节点、左子树、右子树;在中序遍历中,节点的访问顺序是左子树、根节点、右子树;在后序遍历中,节点的访问顺序是左子树、右子树、根节点。
3. 二叉树的应用二叉树在计算机科学领域有着广泛的应用,例如用于构建文件系统、在数据库中存储有序数据、实现算法中的搜索和排序等。
掌握二叉树的遍历方式对于理解这些应用场景非常重要。
三、树1. 树的定义树是一种抽象数据类型,由n(n>0)个节点组成一个具有层次关系的集合。
树的特点是每个节点都有零个或多个子节点,而这些子节点又构成了一颗子树。
树中最顶层的节点称为根节点。
2. 树的遍历树的遍历方式有先根遍历、后根遍历和层次遍历。
在先根遍历中,节点的访问顺序是根节点、子树1、子树2...;在后根遍历中,节点的访问顺序是子树1、子树2...,根节点;在层次遍历中,节点的访问顺序是从上到下、从左到右依次访问每个节点。
3. 树的应用树广泛用于分层数据的表示和操作,例如在计算机网络中的路由算法、在操作系统中的文件系统、在程序设计中的树形结构等。
树的遍历方式对于处理这些应用来说至关重要。
四、森林1. 森林的定义森林是n(n>=0)棵互不相交的树的集合。
每棵树都是一颗独立的树,不存在交集。
2. 森林的遍历森林的遍历方式是树的遍历方式的超集,对森林进行遍历就是对每棵树进行遍历的集合。
3. 森林的应用森林在实际编程中经常用于解决多个独立树结构的问题,例如在数据库中对多个表进行操作、在图像处理中对多个图形进行处理等。



第7章树和森林树形结构是一类重要的非线性结构。
树形结构的特点是结点之间具有层次关系。
本章介绍树的定义、存储结构、树的遍历方法、树和森林与二叉树之间的转换以及树的应用等内容。
重点提示:●树的存储结构●树的遍历●树和森林与二叉树之间的转换7-1 重点难点指导7-1-1 相关术语1.树的定义:树是n(n>=0)个结点的有限集T,T为空时称为空树,否则它满足如下两个条件:①有且仅有一个特定的称为根的结点;②其余的结点可分为m(m>=0)个互不相交的子集T1,T2,…,T m,其中每个子集本身又是一棵树,并称为根的子树。
要点:树是一种递归的数据结构。
2.结点的度:一个结点拥有的子树数称为该结点的度。
3.树的度:一棵树的度指该树中结点的最大度数。
如图7-1所示的树为3度树。
4.分支结点:度大于0的结点为分支结点或非终端结点。
如结点a、b、c、d。
5.叶子结点:度为0的结点为叶子结点或终端结点。
如e、f、g、h、i。
6.结点的层数:树是一种层次结构,根结点为第一层,根结点的孩子结点为第二层,…依次类推,可得到每一结点的层次。
7.兄弟结点:具有同一父亲的结点为兄弟结点。
如b、c、d;e、f;h、i。
8.树的深度:树中结点的最大层数称为树的深度或高度。
9.有序树:若将树中每个结点的子树看成从左到右有次序的(即不能互换),则称该树为有序树,否则称为无序树。
10.森林:是m棵互不相交的树的集合。
7-1-2 树的存储结构1.双亲链表表示法以图7-1所示的树为例。
(1)存储思想:因为树中每个元素的双亲是惟一的,因此对每个元素,将其值和一个指向双亲的指针parent构成一个元素的结点,再将这些结点存储在向量中。
(2)存储示意图:-1 data:parent:(3)注意: Parrent域存储其双亲结点的存储下标,而不是存放结点值。
下面的存储是不正确的:-1 data:parent:2.孩子链表表示法(1)存储思想:将每个数据元素的孩子拉成一个链表,链表的头指针与该元素的值存储为一个结点,树中各结点顺序存储起来,一般根结点的存储号为0。
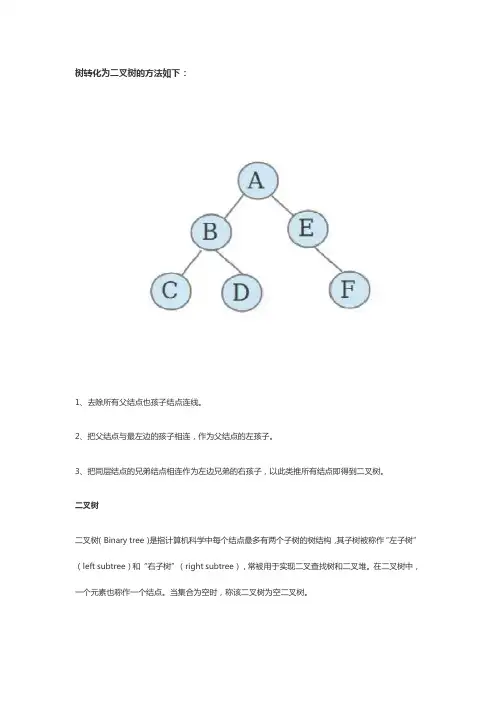
树转化为二叉树的方法如下:
1、去除所有父结点也孩子结点连线。
2、把父结点与最左边的孩子相连,作为父结点的左孩子。
3、把同层结点的兄弟结点相连作为左边兄弟的右孩子,以此类推所有结点即得到二叉树。
二叉树
二叉树(Binary tree)是指计算机科学中每个结点最多有两个子树的树结构,其子树被称作“左子树”(left subtree)和“右子树”(right subtree),常被用于实现二叉查找树和二叉堆。
在二叉树中,一个元素也称作一个结点。
当集合为空时,称该二叉树为空二叉树。
二叉树的遍历,遍历是对树的一种最基本的运算,所谓遍历二叉树,就是按一定的规则和顺序走遍二叉树的所有结点,使每一个结点都被访问一次,而且只被访问一次。
由于二叉树是非线性结构,因此,树的遍历实质上是将二叉树的各个结点转换成为一个线性序列来表示。
设L、D、R分别表示遍历左子树、访问根结点和遍历右子树,则对一棵二叉树的遍历有三种情况:DLR(称为先根次序遍历),LDR(称为中根次序遍历),LRD(称为后根次序遍历)。

二叉树转换为树的规则摘要:一、二叉树与树的定义1.二叉树的定义2.树的定义二、二叉树转换为树的规则1.树的根节点2.树的层次结构3.树的节点关系三、转换方法与步骤1.遍历二叉树2.构建树结构3.确定节点关系四、转换过程中的注意事项1.避免重复遍历2.确保节点唯一性3.考虑节点顺序正文:二叉树与树是计算机科学中常用的数据结构,它们在数据存储与处理方面具有重要作用。
二叉树是一种特殊的树结构,每个节点最多只有两个子节点,分别称为左子节点和右子节点。
在实际应用中,有时需要将二叉树转换为树结构。
本文将详细介绍二叉树转换为树的规则及方法。
首先,我们需要了解二叉树与树的定义。
二叉树是一种特殊的树结构,它的每个节点最多有两个子节点,分别称为左子节点和右子节点。
树是一种非线性的数据结构,由若干个节点组成,这些节点通过边相互连接,具有唯一的根节点。
二叉树转换为树的规则主要包括以下几点:1.树的根节点:二叉树的根节点将成为树的根节点。
2.树的层次结构:二叉树的层次结构将转换为树的层次结构。
具体来说,二叉树的同一层节点将转换为树的同一行节点。
3.树的节点关系:二叉树中相邻的兄弟节点在树中将成为兄弟节点或子节点。
对于二叉树的每个节点,它的左子节点将成为树的子节点,右子节点将成为兄弟节点。
需要注意的是,在转换过程中要确保节点关系的正确性。
接下来,我们介绍二叉树转换为树的步骤:1.遍历二叉树:首先需要遍历二叉树,获取每个节点的信息,如节点值、左右子节点等。
2.构建树结构:根据遍历得到的节点信息,构建树的层次结构。
树的根节点即为二叉树的根节点,树的层次结构应与二叉树的层次结构保持一致。
3.确定节点关系:根据二叉树中节点之间的关系,确定树中节点之间的关系。
具体来说,二叉树的左子节点将成为树的子节点,右子节点将成为兄弟节点。
在二叉树转换为树的过程中,需要注意以下几点:1.避免重复遍历:在遍历二叉树时,应尽量避免重复遍历同一节点,以提高转换效率。

二叉树转化为树的例题二叉树转化为树的例题介绍:二叉树是计算机科学中常见的数据结构之一。
在某些情况下,我们需要将二叉树转化为树。
本文将通过一个例题来详细讨论如何将二叉树转化为树的过程。
例题描述:给定一棵二叉树,我们需要将其转化为一棵普通树。
具体地说,二叉树的每个节点都有一个左孩子和一个右孩子,而普通树的每个节点可以有多个孩子节点。
解题思路:将二叉树转化为树的关键在于将二叉树中的右孩子节点移到左孩子节点并构建新的树结构。
下面我们将分析并实现该转化过程的算法。
算法步骤:1. 定义一个空的树结构,作为转化后的普通树。
2. 从二叉树的根节点开始遍历,将当前节点的右孩子移动到左孩子,并将左孩子添加到树中。
3. 对于每个节点,如果它有左孩子,则将其添加到树中并将其左孩子置为空。
4. 将当前节点设置为它原来的右孩子。
5. 重复步骤2-4,直到所有节点都被处理完。
6. 返回转化后的树结构。
注意事项:在实现算法之前,我们需要考虑可能出现的边界情况和异常输入,例如空二叉树或只有根节点的情况。
代码实现示例(Python):```pythonclass TreeNode:def __init__(self, val):self.val = valself.children = []def binary_tree_to_tree(root):if not root:return Nonenew_root = TreeNode(root.val)if root.left:new_root.children.append(binary_tree_to_tree(root.left)) root.left = Noneif root.right:new_root.children.append(binary_tree_to_tree(root.right)) root.right = Nonereturn new_root```总结:本文讨论了如何将二叉树转化为树的例题。

数据结构详细教案——树与二叉树一、教学目标1.了解树和二叉树的基本概念和特点;2.掌握树和二叉树的基本操作;3.能够通过递归遍历树和二叉树。
二、教学重难点1.树和二叉树的基本概念和特点;2.递归遍历树和二叉树。
三、教学内容1.树的概念和特点1.1树的定义树是n(n>=0)个节点的有限集。
当n=0时,称为空树;如果不为空树,则1. 树有且仅有一个特殊节点被称为根(Root);2.其余节点可分为m(m>0)个互不相交的有限集T1,T2,...,Tm,其中每个集合又是一棵树。
1.2节点间的关系- 父节点(parent)是当前节点的直接上级节点;- 子节点(child)是当前节点的直接下级节点;- 兄弟节点(sibling)是具有同一父节点的节点;- 祖先节点(ancestor)是通过从当前节点到根的任意路径可以到达的节点;- 子孙节点(descendant)是通过从该节点到子树的任意节点可以到达的节点。
1.3树的特点-树是一个有层次的结构,可以看作是一个鱼骨图;-树中的每个节点都可以有多个子节点,但只有一个父节点;-树中的节点之间是唯一的,不存在重复节点;-树中的任意两个节点之间都有且仅有一条路径连接。
2.二叉树的概念和特点2.1二叉树的定义二叉树是一种特殊的树结构,它的每个节点最多只能有两个子节点,分别称为左子节点和右子节点。
2.2二叉树的特点-二叉树的度最大为2,即每个节点最多有两个子节点;-二叉树的第i层最多有2^(i-1)个节点;-对于任意一颗二叉树,如果其叶子节点数为n0,度为2的节点数为n2,则有n0=n2+1;-完全二叉树是一种特殊的二叉树,除了最后一层的叶子节点外,每一层的节点都是满的。
四、教学过程1.讲解树和二叉树的基本概念和特点,引导学生理解树和二叉树的定义和节点间的关系。
2.分析树和二叉树的基本操作,并通过实例演示操作过程,让学生掌握操作的步骤和方法。
3.运用递归算法遍历树和二叉树的过程,详细讲解前序遍历、中序遍历和后序遍历的定义和实现方法。

二叉树,树,森林互相转化的题
二叉树、树和森林是数据结构中常见的概念,它们之间可以相互转化。
首先我们来看一下它们的定义和特点。
二叉树是一种特殊的树结构,每个节点最多有两个子节点,分别为左子节点和右子节点。
树是由n(n>=1)个节点组成的有限集合,它们之间存在唯一的父子关系。
而森林是由若干棵互不相交的树组成。
现在我们来看一下它们之间的转化关系:
1. 二叉树转化为树,将二叉树的左子节点作为树的子节点,右子节点作为兄弟节点,这样就可以将二叉树转化为树。
2. 树转化为二叉树,将树的每个节点的第一个子节点作为二叉树的左子节点,其余的子节点作为左子节点的右子节点,这样就可以将树转化为二叉树。
3. 树转化为森林,如果一个树有多个子节点,可以将它的子节点拆分成多棵树,这样就可以将树转化为森林。
4. 森林转化为树,将森林中的每棵树的根节点作为新树的子节点,这样就可以将森林转化为树。
通过以上转化方法,我们可以实现二叉树、树和森林之间的互相转化。
这些转化方法在实际的数据结构操作中有着重要的应用,能够帮助我们更好地理解和利用这些数据结构。
在实际编程中,我们可以根据具体的需求选择合适的数据结构,并通过转化实现各种操作和算法。
希望这些信息能够对你有所帮助。
树转换成二叉树的方法树转换成二叉树的方法树是一种非常常见的数据结构,但是在某些情况下,我们需要将树转换成二叉树。
这里,我们将详细介绍如何将一棵普通的树转换成二叉树。
1. 什么是二叉树?在介绍如何将树转换成二叉树之前,我们需要先了解什么是二叉树。
二叉树是一种特殊的树形结构,每个节点最多有两个子节点,分别称为左子节点和右子节点。
同时,左子节点的值必须小于等于父节点的值,右子节点的值必须大于等于父节点的值。
2. 树转换成二叉树的方法将一棵普通的树转换成二叉树可以分为以下几个步骤:2.1 将每个节点的第一个子节点作为其左子节点对于每个节点来说,它可能有多个子节点。
我们可以将第一个子节点作为它的左子节点,并且将其他子节点插入到它左侧相邻兄弟节点的右边。
这样就能够保证每个节点最多只有两个子节点。
2.2 将所有右侧相邻兄弟节点都作为其父亲或者祖先节点的右子节点对于每个节点的右侧相邻兄弟节点,我们需要将它们插入到它们的父亲或者祖先节点的右子树中。
如果当前节点没有父亲或者祖先节点,则需要创建一个虚拟的根节点,并将其作为新的父亲节点。
2.3 递归地将所有子树转换成二叉树对于每个子树来说,我们需要递归地进行转换操作,直到所有子树都被转换成了二叉树。
3. 代码实现下面是将一棵普通的树转换成二叉树的代码实现:```class TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightdef treeToBinaryTree(root: ''Node'') -> TreeNode:if not root:return None# 将第一个子节点作为左子节点,其他兄弟节点插入到左侧相邻兄弟右边for child in root.children[1:]:child.left = root.leftroot.left.right = childroot.left = child# 将右侧相邻兄弟插入到父亲或者祖先节点的右子树中if root.children:node = treeToBinaryTree(root.children[0])for child in root.children[1:]:node.right = treeToBinaryTree(child)node = node.right# 递归地将所有子树转换成二叉树root.left = treeToBinaryTree(root.left)root.right = Nonereturn root```4. 总结将一棵普通的树转换成二叉树可以通过将每个节点的第一个子节点作为其左子节点,将所有右侧相邻兄弟节点都作为其父亲或者祖先节点的右子节点,以及递归地将所有子树转换成二叉树来实现。
数据结构课程设计_⼆叉树操作数据结构课程设计题⽬:⼆叉树的操作学⽣姓名:学号:系部名称:计算机科学与技术系专业班级:指导教师:课程设计任务书第⼀章程序要求1)完成⼆叉树的基本操作。
2)建⽴以⼆叉链表为存储结构的⼆叉树;3)实现⼆叉树的先序、中序和后序遍历;4)求⼆叉树的结点总数、叶⼦结点个数及⼆叉树的深度。
第⼆章算法分析建⽴以⼆叉链表为存储结构的⼆叉树,在次⼆叉树上进⾏操作;1先序遍历⼆叉树的操作定义为:若⼆叉树唯恐则为空操作;否则(1)访问根节点;(2)先序遍历做字数和;(3)先序遍历有⼦树;2中序遍历⼆叉树的操作定义为:若⼆叉树为空,则空操作;否则(1)中序遍历做⼦树;(2)访问根节点;(3)中序遍历有⼦树;3后续遍历⼆叉树的操作定义为:若⼆叉树为空则为空操作;否则(1)后序遍历左⼦树;(2)后序遍历右⼦树;(3)访问根节点;⼆叉树的结点总数、叶⼦结点个数及⼆叉树的深度。
第三章⼆叉树的基本操作和算法实现⼆叉树是⼀种重要的⾮线性数据结构,是另⼀种树形结构,它的特点是每个节点之多有两棵⼦树(即⼆叉树中不存在度⼤于2的结点),并且⼆叉树的结点有左右之分,其次序不能随便颠倒。
1.1⼆叉树创建⼆叉树的很多操作都是基于遍历实现的。
⼆叉树的遍历是采⽤某种策略使得采⽤树形结构组织的若⼲年借点对应于⼀个线性序列。
⼆叉树的遍历策略有四种:先序遍历中续遍历后续遍历和层次遍历。
基本要求1 从键盘接受输⼊数据(先序),以⼆叉链表作为存储结构,建⽴⼆叉树。
2 输出⼆叉树。
3 对⼆叉树进⾏遍历(先序,中序,后序和层次遍历)4 将⼆叉树的遍历打印出来。
⼀.问题描述⼆叉树的很多操作都是基于遍历实现的。
⼆叉树的遍历是采⽤某种策略使得采⽤树型结构组织的若⼲结点对应于⼀个线性序列。
⼆叉树的遍历策略有四种:先序遍历、中序遍历、后序遍历和层次遍历。
⼆.基本要求1.从键盘接受输⼊数据(先序),以⼆叉链表作为存储结构,建⽴⼆叉树。
2.输出⼆叉树。
树、森林与二叉树的转换1、树转换为二叉树由于二叉树是有序的,为了避免混淆,对于无序树,我们约定树中的每个结点的孩子结点按从左到右的顺序进行编号。
将树转换成二叉树的步骤是:(1)加线。
就是在所有兄弟结点之间加一条连线;(2)抹线。
就是对树中的每个结点,只保留他与第一个孩子结点之间的连线,删除它与其它孩子结点之间的连线;(3)旋转。
就是以树的根结点为轴心,将整棵树顺时针旋转一定角度,使之结构层次分明。
树转换为二叉树的过程示意图2、森林转换为二叉树森林是由若干棵树组成,可以将森林中的每棵树的根结点看作是兄弟,由于每棵树都可以转换为二叉树,所以森林也可以转换为二叉树。
将森林转换为二叉树的步骤是:(1)先把每棵树转换为二叉树;(2)第一棵二叉树不动,从第二棵二叉树开始,依次把后一棵二叉树的根结点作为前一棵二叉树的根结点的右孩子结点,用线连接起来。
当所有的二叉树连接起来后得到的二叉树就是由森林转换得到的二叉树。
森林转换为二叉树的转换过程示意图3、二叉树转换为树二叉树转换为树是树转换为二叉树的逆过程,其步骤是:(1)若某结点的左孩子结点存在,将左孩子结点的右孩子结点、右孩子结点的右孩子结点……都作为该结点的孩子结点,将该结点与这些右孩子结点用线连接起来;(2)删除原二叉树中所有结点与其右孩子结点的连线;(3)整理(1)和(2)两步得到的树,使之结构层次分明。
二叉树转换为树的过程示意图4、二叉树转换为森林二叉树转换为森林比较简单,其步骤如下:(1)先把每个结点与右孩子结点的连线删除,得到分离的二叉树;(2)把分离后的每棵二叉树转换为树;(3)整理第(2)步得到的树,使之规范,这样得到森林。
根据树与二叉树的转换关系以及二叉树的遍历定义可以推知,树的先序遍历与其转换的相应的二叉树的先序遍历的结果序列相同;树的后序遍历与其转换的二叉树的中序遍历的结果序列相同;树的层序遍历与其转换的二叉树的后序遍历的结果序列相同。
由森林与二叉树的转换关系以及森林与二叉树的遍历定义可知,森林的先序遍历和中序遍历与所转换得到的二叉树的先序遍历和中序遍历的结果序列相同。
《数据结构》课程设计报告设计题目:_树与二叉树的转换___姓名:_______李锦_____________学号:________211214011_______专业:_______物联网工程_______院系:_______计算机科学与技术_______班级:__________1205___________指导教师:_________高秀梅______ 2014年 2 月14 日目录一、问题描述 (2)二、基本要求 (2)三、概要设计 (2)四、数据结构设计 (2)五、算法设计 (3)1、算法分析 (3)2、算法实现 (3)六、程序测试与实现 (6)1、函数之间的调用关系 (6)2、主程序 (6)3、测试数据 (8)4、测试结果 (8)七、调试分析 (10)八、遇到的问题及解决办法 (10)九、心得体会 (10)一、问题描述完成树与二叉树的转换二、基本要求1、树采用双亲表示法2、能够将树转换为二叉树3、对转换的二叉树进行算法设计统计人一结点的孩子数4、利用转换的二叉树计算树的高度三、概要设计操作集合:(1) CTreeNode *SearchCTree(CTreeNode *root ,char data) 查找树结点(2) CTreeNode *CreateSTree() 生成树(3) void preorderTree(CTreeNode *ctroot) 树的遍历(4) void PrintTree(CTreeNode *troot,int depth) 树的输出(5 void initQueueCTree(QueueCTree *&q) 初始化树队列(6) void initQueueBTree(QueueBTree *&q) 初始化二叉树队列(7)void TreeToBTree(CTreeNode *ctroot,BTreeNode *&btroot) //树转化为二叉树ctroot指向树的根节点,btroot,指向二叉树的根四、数据结构设计struct CTreeNode//树节点的类型{char data;//数据域,采用char星struct CTreeNode *children[DEGREE];//指向孩子节点的指针域};struct BTreeNode{char data;//数据域BTreeNode *lchild,*rchild;//左右孩子节点的指针};//树队列结构体类型struct QueueCTree{CTreeNode *CTreeArray[MAX_NODE_NUM];//结构体指针数组,存放节点的地址//struct nodeCTree *next;int CTreeFront,CTreeRear;};//二叉树队列结构类型struct QueueBTree{BTreeNode *BTreeArray[MAX_NODE_NUM];//结构体指针数组,存放节点的地址//struct nodeBTree *next;int BTreeFront,BTreeRear;};五、算法设计1、算法分析将树转换成二叉树的步骤是:(1)加线。
就是在所有兄弟结点之间加一条连线;(2)抹线。
就是对树中的每个结点,只保留他与第一个孩子结点之间的连线,删除它与其它孩子结点之间的连线;(3)旋转。
就是以树的根结点为轴心,将整棵树顺时针旋转一定角度,使之结构层次分明。
2、算法实现void TreeToBTree(CTreeNode *ctroot,BTreeNode *&btroot)//树转化为二叉树ctroot 指向树的根节点,btroot,指向二叉树的跟{QueueCTree *VisitedCTreeNodes;QueueBTree *VisitedBTreeNodes;//辅助队列initQueueCTree(VisitedCTreeNodes);initQueueBTree(VisitedBTreeNodes);//初始化队列CTreeNode *ctnode;BTreeNode *btnode,*p,*LastSibling;int i;btroot=new BTreeNode;//添加开辟内存空间语句btroot->data=ctroot->data;//树的根节点作为二叉树的根节点btroot->lchild=btroot->rchild=NULL;addQueueCTree(VisitedCTreeNodes,ctroot);//树的跟节点入队addQueueBTree(VisitedBTreeNodes,btroot);//二叉树的跟节点入队while(!QueueCTreeEmpty(VisitedCTreeNodes)){ctnode=delQueueCTree(VisitedCTreeNodes);//树节点出队btnode=delQueueBTree(VisitedBTreeNodes);//二叉树节点出队for(i=0;i<DEGREE;i++)//访问节点所有的孩子节点{if(ctnode->children[i]==NULL)//孩子节点访问完毕break;p=new BTreeNode;//分配二叉树节点p->data=ctnode->children[i]->data;p->lchild=p->rchild=NULL;if(i==0)btnode->lchild=p;//长子,作为父节点的做孩子elseLastSibling->rchild=p;//作为上一个兄弟节点的右孩子LastSibling=p;addQueueCTree(VisitedCTreeNodes,ctnode->children[i]);//树节点进队列addQueueBTree(VisitedBTreeNodes,p);//二叉树节点进门队列}3、算法流程图六、程序测试与实现1、函数之间的调用关系2、主程序int main(){CTreeNode *Tree;BTreeNode *BTree;int x=0;char n,i,j,k;while(1){p:n=menu();if(n=='1'){while(1){i=Treemenu();switch(i){case '1':Tree=CreateSTree();break;case '2':PrintTree(Tree,10);cout<<"\n\t\t按任意键返回...\n";getch();break;case '3':preorderTree(Tree);cout<<"\n\t\t按任意键返回...\n";getch();break;case '4':goto p;break;}}}if(n=='2'){TreeToBTree(Tree,BTree);while(1){j=Btreemenu();switch(j){case '1':PrintIn(BTree,5);cout<<"\n\t\t按任意键返回...\n";getch();break;case '2':Preorder(BTree);cout<<"\n\t\t按任意键返回...\n";getch();break;case '3':cout<<FindDepth(BTree);cout<<"\n\t\t按任意键返回...\n";getch();break;case '4':count(BTree);cout<<"\n\t\t按任意键返回...\n";getch();break;case '5':goto p;break;}}}if(n=='3'){break;}}return 0;}3、测试数据a b c d e4、测试结果七、调试分析首先根据指令,输入信息,生成一个树后,再将生成的树转化成二叉树,然后输出二叉树的结构图,二叉树的前序遍历结果以及二叉树的深度和节点孩子数八、遇到的问题及解决办法调试时遇到诸多问题,其中最主要的问题是死循环问题,在非递归遍历时,容易进入死循环,经过查找资料、分步调试最终找到循环结束条件,顺利解决各个难题。
九、心得体会通过本次课程设计,我发现,有关一个课题的所有知识不仅仅是在课本上,多查阅一些资料能够更好的完成课题,这就需要一种能力,即自学能力。
本次课程设计还让我认识到自己的缺点。
本次选的课题是二叉树的遍历,因为本学期所学的就是二叉树等数据结构,所以认为比较适合。
刚开始认为会很简单,但到后来就出现一些难以解决的问题,就像老师请教,并查阅相关资料。
经过慢慢的调试,最终测试成功。
这次课程设计让我所学到的数据结构知识发挥的淋漓尽致,而且还拓展了我的知识面,使我更加熟练的掌握各种方法。
总之,这次课程设计增强了我的自学能力,拓展了我的知识面,让我对数据结构更加了解。