电磁学第四版课后答案解析 梁灿彬

电磁场 与电磁波（第四版） 课后答案第一章 习 题 解答1.1 给定三个矢量A 、B 和C 如下： 23x y z =+-A e e e4y z =-+B e e 52x z =-C e e求：（1）A a ；（2）-A B ；（3）A B ；（4）AB θ；（5）A 在B 上的 分量；（6）⨯A C ；（7）()⨯A B C 和()⨯A B C ；（8）()⨯⨯A B C 和()⨯⨯A B C 。

解 （1）23A x y z +-===e e e A a e e e A （2）-=A B (23)(4)x y z y z +---+=e e e ee 64x y z +-=e e e （3）=A B (23)x y z +-e e e (4)y z -+=e e －11 （4）由cos AB θ=14-==⨯A B AB ，得1cos AB θ-=(135.5= （5）A 在B 上的分 量 B A =A cos AB θ=1117=-A B B （6）⨯=A C 123502x yz-=-e e e 41310x y z ---e e e（7）由于⨯=B C 041502x yz-=-e e e 8520x y z ++e e e⨯=A B 123041xyz-=-e e e 1014x y z ---e e e所以 ()⨯=A B C (23)x y z +-e e e (8520)42x y z ++=-e e e ()⨯=A B C (1014)x y z ---e e e (52)42x z -=-e e（8）()⨯⨯=A B C 1014502x y z---=-e e e 2405x y z -+e e e()⨯⨯=A B C 1238520xy z -=e e e 554411x y z --e e e1.2 三角形的三个顶点 为1(0,1,2)P -、2(4,1,3)P -和3(6,2,5)P 。

///5．1．1 解答：(1) 质子所受洛伦兹力的方向向东(2) 质子的电荷量191.610q C -=⨯，质子所受洛伦兹力大小为163.210F qvB N -==⨯质子的质量271.6710m kg -=⨯，质子所受洛伦兹力与受到的地球引力相比较：101.9510F qvB F mg==⨯洛重 5．2．1 解答：O 点的磁场B 可看作两条半无限长直载流导线产生的磁场1B 、2B 和MN 部分阶段1/4圆周载流导线产生的磁场3B 的合成。

由于磁场方向均垂直纸面向外，所以直接求出它们大小并相加即可0012cos0cos 424I IB B R Rμμπππ⎛⎫==-=⎪⎝⎭ 40032448I IB Rd R Rππμμαπ-==⎰0123124I B B B B R μππ⎛⎫=++=+ ⎪⎝⎭方向垂直纸面向外 5．2．2 解答：（a ）延长线通过圆心的直长载流导线在O 点产生磁场为1B ，其大小为0；另一直长载流导线在O 点产生的磁场为2B ，方向垂直纸面向里；圆弧部分载流导线在O 点产生的磁场为3B ，方向垂直纸面向里。

故O 点的合磁场大小为0001233314842I I I B B B B R R R μμμπππ⎛⎫=++=+=+ ⎪⎝⎭方向垂直纸面向里（b ）两半直长载流导线在O 点产生的磁场分别为1B 、2B ，方向均垂直纸面向里；圆弧部分载流导线在O 点产生的磁场为3B ，方向垂直纸面向里。

故O 点的合磁场大小为()000012324444I I I IB B B B R R R Rμμμμππππ=++=++=+ 方向垂直纸面向里 5．2．3 解答：（a ）因为两直长载流导线延长线均通过圆心，所以对O 点的磁场没有贡献，故只需要考虑两个圆弧载流导线在O 点产生的磁场，它们所激发的磁场分别为1B 、2B ，方向均垂直纸面向里，故O 点的合磁场大小为00123312248I I B B B a b a b ππμμπ⎛⎫⎪⎛⎫=+=+=+ ⎪ ⎪⎝⎭ ⎪⎝⎭方向均垂直纸面向里（b ）两延长线的直长载流导线对O 点的磁场没有贡献，只需要考虑两长度为b 的直长载流导线对O 点的磁场1B 、2B 和圆弧载流导线对O 点的磁场3B ，方向均垂直纸面向里，其合磁场大小为()0001232332cos90cos13524442a I I I B B B B b a b a πμμμππππ⎛⎫⎛⎫⎪=++=-⨯+=+ ⎪ ⎪ ⎪⎝⎭ ⎪⎝⎭方向均垂直纸面向里。

3．2．1 解答：（1）如图3.2.1所示，偶极子的电荷量q 和q -所受的电场力分别为qE 和qE -，大小相等，合力为0，但所受的力矩为M P E =⨯当且仅当0θ=和θπ=时，电偶极子受的力矩为0，达到平衡状态，但在0θ=的情况下稍受微扰，电偶极子将受到回复力矩回到平衡位置上，因此，0θ=时，是稳定平衡；但在θπ=的情况下稍受微扰，电偶极子受到的力矩将使电偶极子“倾覆”到达0θ=情况，因此，θπ=的情况是不稳定平衡。

（2）若E 不均匀，一般情况下，偶极子的电荷量q 和q -所受的电场力不为0，电场力将使偶极子转向至偶极矩P 与场强E 平行的情况，由于电场不均匀，偶极子所受的合力不为0.因此,电偶极子不能达到平衡状态。

3．2．2 解答：（1）如图3.2.2所示，偶极子1P 和2P 中的2q -处激发的电场为13222p E kl r -=⎛⎫- ⎪⎝⎭2q -所受的电场力为2123222q p F q E kl r ---=-=⎛⎫- ⎪⎝⎭偶极子1P 和2P 中的2q 处激发的电场为13222p E kl r +=⎛⎫+ ⎪⎝⎭2q 所受的电场力为2123222q p F q E kl r ++==⎛⎫+ ⎪⎝⎭偶极子2P 受到的合力为()332221222l l F F F k q p r r --+-⎡⎤⎛⎫⎛⎫=+=+--⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦令22l x ≡，()()3f x r x -≡+，()()3g x r x -≡-，则()()330,0f r g r --==，故()()()()()()4444'3,'3,'03,'03f x r x g x r x f r g r ----=-+=-=-=因22l r >>，对22l r ⎛⎫+ ⎪⎝⎭和22l r ⎛⎫- ⎪⎝⎭在0r =处展开后，略去高次项 ()()()()()()3434'003,0'03f x f x f r r x g x g g x r r x ----≈+=-=+=+()()46f x g x xr --=-所以()42121221440033(2)62q p l p p F k q p xr r rπεπε--=-=-= 其大小为124032p p F r πε=以上是1P 和2P 同向的情况，反向时大小不变，受力方向相反。

电磁学习题解答1．2．2两个同号点电荷所带电荷量之和为Q 。

在两者距离一定的前提下，它们带电荷量各为多少时相互作用力最大？解答：设一个点电荷的电荷量为1q q =，另一个点电荷的电荷量为2()q Q q =-，两者距离为r ，则由库仑定律求得两个点电荷之间的作用力为令力F 对电荷量q 的一队导数为零，即 得即取122Qq q ==时力F 为极值，而 故当122Qq q ==时，F 取最大值。

1．2．3两个相距为L 的点电荷所带电荷量分别为2q 和q ，将第三个点电荷放在何处时，它所受的合力为零？解答：要求第三个电荷Q 所受的合力为零，只可能放在两个电荷的连线中间，设它与电荷q 的距离为了x ，如图1.2.3所示。

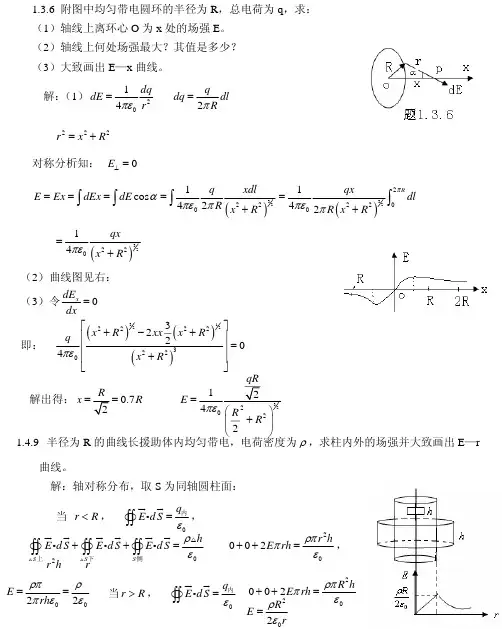
电荷Q 所受的两个电场力方向相反，但大小相等，即得2220x Lx L +-=舍去0x <的解，得1)x L =- 1．3．8解答:（1）先求竖直无限长段带电线在O 点产生的场强1E ϖ，由习题1.3.7（2）可知104x E Rηπε=仿习题1.3.7解答过程，得故10ˆˆ()4E i j Rηπε=-v 同理，水平无限长段带电线在O 点产生的场强对于圆弧段带电线在O 点产生的场强3E ϖ，参看图1.3.8（b ），得同理得304y E Rηπε=故30ˆˆ()4E i j Rηπε=+v 解得（2）利用（1）中的结论，参看习题1.3.8图（b ），A -∞的带电直线在O 点的场强为B -∞的带电直线在O 点产生的场强为根据对称性，圆弧带电线在O 点产生的场强仅有x 分量，即 故带电线在O 点产生的总场强为 1．3．9解答:在圆柱上取一弧长为Rd ϕ、长为z 的细条，如图（a ）中阴影部分所示，细条所带电荷量为()dq zRd σϕ=，所以带电细条的线密度与面密度的关系为由习题1.3.7知无限长带电线在距轴线R 处产生的场强为图（b ）为俯视图，根据对称性，无限长带电圆柱面轴线上的场强仅有x 分量，即 1．4．5解答：如图所示的是该平板的俯视图，OO ′是与板面平行的对称平面。

电磁场与电磁波（第四版）课后答案第一章习题解答1.1 给定三个矢量A 、B 和C 如下： 23x y z =+-A e e e4y z =-+B e e52x z =-C e e求：（1）A a ；（2）-A B ；（3）A B ；（4）AB θ；（5）A 在B 上的分量；（6）⨯A C ；（7）()⨯A B C 和()⨯A B C ；（8）()⨯⨯A B C 和()⨯⨯A B C。

解 （1）23A x y z+-===+-e e e A a e e e A （2）-=A B (23)(4)x y z y z +---+=e e e e e 64x y z +-e e e （3）=A B (23)x y z +-e e e (4)y z -+=e e －11 （4）由c o s AB θ=11238=A B A B ，得1c o sAB θ-=(135.5= （5）A 在B 上的分量 B A=A c o s AB θ==A B B （6）⨯=A C 123502xyz-=-e e e 41310x y z ---e e e （7）由于⨯=B C 041502x y z-=-e e e 8520x y z ++e e e⨯=A B 123041xyz-=-e e e 1014x y z ---e e e所以 ()⨯=A B C (23)x y z +-e e e (8520)42x y z ++=-e e e ()⨯=A B C (1014)x y z ---e e e (52)42x z -=-e e （8）()⨯⨯=A B C 1014502xyz---=-e e e 2405x y z -+e e e()⨯⨯=A B C 1238520x y z -=e e e 554411x y z --e e e1.2 三角形的三个顶点为1(0,1,2)P -、2(4,1,3)P -和3(6,2,5)P 。

普通物理学教程：电磁学引言电磁学是物理学的一个重要分支，研究电荷在空间中的分布和相互作用。

本教程旨在介绍电磁学的基本概念和原理，帮助读者理解电磁学的基本知识和应用。

1. 电荷和电场1.1 电荷电荷是物质的一种属性，它分为正电荷和负电荷。

电荷之间存在相互作用力，这种力称为电荷间的库仑力。

1.2 电场电场是电荷在周围空间产生的一种物理量，它可以用来描述电荷之间相互作用的方式。

电场可以通过电场线来直观地表示，电场线指示了电场的强度和方向。

在电场中，电荷会受到电场力的作用。

2. 静电场和电势2.1 静电场静电场是指所有电荷都处于静止状态时产生的电场。

静电场的特点是电场强度只与电荷的分布有关，与电荷的运动状态无关。

2.2 电势电势是描述电场能量的一种物理量，它表示单位正电荷在电场中所具有的能量。

电势可以通过电势线来表示，电势线距离越近，电势越高。

3. 电容和电容器3.1 电容电容是描述物体存储电荷能力的物理量，它与物体的几何形状和介质的性质密切相关。

3.2 电容器电容器是存储电荷的装置，常见的电容器有平行板电容器和球面电容器。

电容器的电容可以通过电容公式计算。

4. 电流和电阻4.1 电流电流是描述电荷运动情况的物理量，它表示单位时间内通过导体横截面的电荷量。

4.2 电阻电阻是物体对电流流动的阻碍程度，它是导体材料的一种性质。

电阻与导体的长度、横截面积和电阻率有关。

5. 磁场和磁感应5.1 磁场磁场是磁荷在周围空间产生的一种物理量，它可以用来描述磁荷之间相互作用的方式。

磁场可以通过磁力线来直观地表示，磁力线指示了磁场的强度和方向。

在磁场中，磁荷会受到磁场力的作用。

5.2 磁感应磁感应是指物体受到磁场作用后表现出的一种物理现象，它可以通过磁感应线来表示。

6. 电磁感应和法拉第定律6.1 电磁感应电磁感应是指导体中的电磁感应现象，当导体中的磁通量发生变化时，会在导体中产生感应电流。

6.2 法拉第定律法拉第定律描述了电磁感应现象的定量关系，它表明感应电动势等于磁通量的变化率。

实用文档2.1点电荷的严格定义是什么？点电荷是电荷分布的一种极限情况，可将它看做一个体积很小而电荷密度很的带电小球的极限。

当带电体的尺寸远小于观察点至带电体的距离时，带电体的形状及其在的电荷分布已无关紧要。

就可将带电体所带电荷看成集中在带电体的中心上。

即将带电体抽离为一个几何点模型，称为点电荷。

2.2研究宏观电磁场时，常用到哪几种电荷的分布模型？有哪几种电流分布模型？他们是如何定义的？常用的电荷分布模型有体电荷、面电荷、线电荷和点电荷；常用的电流分布模型有体电流模型、面电流模型和线电流模型，他们是根据电荷和电流的密度分布来定义的。

2,3点电荷的电场强度随距离变化的规律是什么？电偶极子的电场强度又如何呢？点电荷的电场强度与距离r 的平方成反比；电偶极子的电场强度与距离r 的立方成反比。

2.4简述E / 和E 0 所表征的静电场特性静电荷是静电场的通量源。

E /表明空间任意一点电场强度的散度与该处的电荷密度有关，E 0表明静电场是无旋场。

2.5表述高斯定律，并说明在什么条件下可应用高斯定律求解给定电荷分布的电场强度。

高斯定律：通过一个任意闭合曲面的电通量等于该面所包围的所有电量的代数和除以与闭合面外的电荷无1关，即E dS dV 在电场（电荷）分布具有某些对称性时，可应用高斯定律求解给定电荷分S 0 V 布的电场强度。

2.6简述 B 0和 B J所表征的静电场特性。

0，磁力线是无关尾的闭合线，B 0表明穿过任意闭合面的磁感应强度的通量等于B J表明恒定磁场是有旋场，恒定电流是产生恒定磁场的漩涡源安培环路定理：磁感应强度沿任何闭合回路的线积分等于穿过这个环路所有电流的代数和0倍，即B dl 0I如果电路分布存在某种对称性，则可用该定理求解给定电流分布的磁感应强度。

C2.8简述电场与电介质相互作用后发生的现象。

在电场的作用下出现电介质的极化现象，而极化电荷又产生附加电场2.9极化强度的如何定义的？极化电荷密度与极化强度又什么关系？单位体积的点偶极矩的矢量和称为极化强度，P 与极化电荷密度的关系为p - P极化强度P 与极化电荷面的密度sp P e n2.10电位移矢量是如何定义的？在国际单位制中它的单位是什么电位移矢量定义为 D 0E P E其单位是库伦/ 平方米（C/m2）2.11简述磁场与磁介质相互作用的物理现象？在磁场与磁介质相互作用时，外磁场使磁介质中的分子磁矩沿外磁场取向，磁介质被磁化，被磁化的介质要产生附加磁场，从而使原来的磁场分布发生变化，磁介质实用文档中的磁感应强度B 可看做真空中传导电流产生的磁感应强度B0 和磁化电流产生的磁感应强度B' 的叠加，即B B 0 B2.12磁化强度是如何定义的？磁化电流密度与磁化强度又什么关系？单位体积内分子磁矩的矢量和称为磁化强度；磁化电流体密度与磁化强度： JM M磁化电流面密度与磁化强度： JSMM e n2.13 磁场强度是如何定义的？在国际单位制中它的单位是什么？磁场强度定义为： H BM 国际单位之中，单位是安培 / 米(A/m)2,14 你理解均匀媒质与非均匀媒质，线性媒质与非线性媒质，各向同性与各向异性媒质的含义么？均匀媒质是指介电常数 0 或磁介质磁导率 处处相等， 不是空间坐标的函数。