下载文档原格式
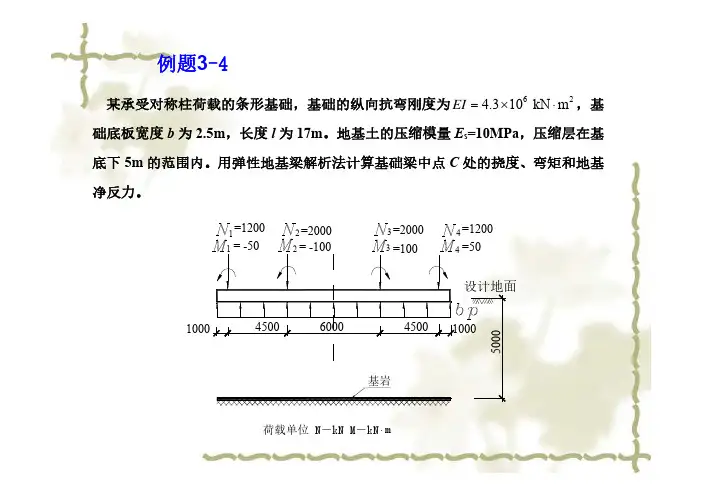
某承受对称柱荷载的条形基础，基础的纵向抗弯刚度为624.310 kN m EI =⨯⋅，基础底板宽度b 为2.5m ，长度l 为17m 。
地基土的压缩模量E s =10MPa ，压缩层在基底下5m 的范围内。
用弹性地基梁解析法计算基础梁中点C 处的挠度、弯矩和地基净反力。
m.荷载单位 N－kN M－kN 基岩=100= -100=50=1200=2000=2000=120043215000600045004500100010004321例题3-4【解】 1）确定地基的基床系数和梁的柔度指数 基底的附加压力近似按地基的平均净反力考虑(12002000)2150.62.517N p bl+⨯===⨯∑ kPa基础中心点的沉降计算，取沉降修正系数Ψs ＝1.0；按薄压缩层计算，取z i -1＝0，z i =5.0m ，基底中心的平均附加应力系数C i 可按地基附加应力计算方法查有关表格求得为0.6024。
于是基础的中心沉降 0150.61.050.60240.045410000s i i s p s z C E ψ==⨯⨯⨯= m 考虑柔性基础中点沉降与平均沉降的差异，根据l /b 查表可求得沉降影响系数ω0、ωm 分别为2.31和2.02。
基础的平均沉降 m002.020.04540.03972.31m s s ωω⎛⎫==⨯=⎪⎝⎭m基床系数 m 150.638000.0397s p k s === kN/m 3集中基床系数 2.538009500s bk =⨯= kPa 柔度指数 4695000.15334 4.310λ==⨯⨯ m -12.6064l πλπ<=< 故属有限长梁。
按无限长梁计算的基础梁左端A 处内力值外荷 载 与A 点距离x （m ）A x C x D x m)kN (⋅a M)kN (a QN 1=1200kN 1.0 0.716900.84782(x C P λ40正对称)=1402.7 (x D P 20-反对称)=508.7 M 1=-50kN-m 1.0 0.978750.84782(x D M20反对称)=21.2 (x A M 20λ-正对称)=3.8N 2=2000kN 5.5 -0.035130.2862 (x C Pλ40正对称)=-114.6 (x D P20-反对称)=286.2 M 2=-100kN-m 5.5 0.613180.2860 (x D M20反对称)=14.3 (x A M 20λ-正对称)=4.7N 3=2000kN 11.5 -0.20113-0.0328 (x C Pλ40正对称)=-656.0 (x D P20-反对称)=-32.8 M 3=100kN-m 11.5 0.13046-0.0320 (x D M20反对称)=1.6 (x A M 20λ-正对称)=-1.0N 4=1200kN 16.0 -0.12111-0.0665 (x C Pλ40正对称)=-237.0 (x D P20-反对称)=-39.9 M 4=50kN-m16.0-0.0115-0.0680(x D M20反对称)=1.7 (x A M 20λ-正对称)=0.04总 计433.9 729.72) 按无限长梁计算基础梁左端A处的内力3) 计算梁端的边界条件力按 2.606l λ=查表得0.02579, 0.10117, D 0.063484.04522, 0.30666l l l l l A C F F =-=-=-==-计算虚拟集中荷载[][]()(1)(1) (4.045220.30666)(10.06348)730.7(10.02579)0.1533433.9 2810.0 kNA B l l l a l a P P E F D Q A M λ==+++-=--⨯++⨯⨯= ()(1)(1)2730.7 (4.045220.30666)(10.10117)(10.06348)33.920.1533 9721.5 kNa A B l l l l a Q M M E F C D M λ⎡⎤=-=-+++-⎢⎥⎣⎦⎡⎤=---⨯++⨯⎢⎥⨯⎣⎦=- 4）计算C 点处的挠度、弯矩和地基的净反力先计算半边荷载引起C 点处的内力，然后根据对称原理计算叠加得出C 点处的挠度C w 、弯矩M C 和地基的净反力p CC 点处的弯矩与挠度计算表（半边荷载作用下）外荷载与边界条件力 C 点相距荷载位置x （m ）M C /2 (kNꞏm)w c /2 (cm)N 1 M 1 N 2 M 2 P A M A7.5 7.5 3.0 3.0 8.5 8.5-312.3 -3.2 931.2 -28.3 -871.2 -349.3 0.405 -0.004 1.365 -0.007 0.757 -0.630 总 计－633.11.886于是2(633.1)1266.2 kN m C M =⨯-=-⋅ 20.01890.0377 m C w =⨯=3800.0377143.3 kPa C s C p k y ==⨯=4）计算C 点处的挠度、弯矩和地基的净反力先计算半边荷载引起C 点处的内力，然后根据对称原理计算叠加得出C 点处的挠度w C 、弯矩M C 和地基的净反力p C。
某框架结构柱下条形基础设计（倒梁法）一、设计资料1、某建筑物为7层框架结构，框架为三跨的横向承重框架，每跨跨度为7.2m ；边柱传至基础顶部的荷载标准值和设计值分别为：Fk=2665KN 、Mk=572KN •M 、Vk=146KN ，F=3331KN 、M=715KN •M 、V=182KN ；中柱传至基础顶部的荷载标准值和设计值分别为：Fk=4231KN 、Mk=481KN •M 、Vk=165KN ，F=5289KN 、M=601KN •M 、V=206KN 。
2、根据现场观察描述，原位测试分析及室内试验结果，整个勘察范围内场地地层主要由粘性土、粉土及粉砂组成，根据土的结构及物理力学性质共分为7层，具体层位及工程特性见附表。
勘察钻孔完成后统一测量了各钻孔的地下水位，水位埋深平均值为0.9m ，本地下水对混凝土无腐蚀性，对钢筋混凝土中的钢筋无腐蚀性。
3、根据地质资料，确定条基埋深d ＝1.9m ； 二、内力计算1、基础梁高度的确定 取h ＝1.5m 符合GB50007-2002 8.3.1柱下条形基础梁的高度宜为柱距的11~48的规定。
2、条基端部外伸长度的确定据GB50007-2002 8.3.1第2条规定外伸长度宜为第一跨的0.25倍考虑到柱端存在弯矩及其方向左侧延伸0.250.257.2 1.8l m m =⨯=为使荷载形心与基底形心重合，右端延伸长度为ef l ，ef l 计算过程如下：a . 确定荷载合力到E 点的距离o x ：333137.2528927.271526012182 1.52206 1.523331252892o x ⨯⨯+⨯⨯-⨯-⨯-⨯⨯-⨯⨯=⨯+⨯得18239610.5817240o x m ==b . 右端延伸长度为ef l ：(1.8 2.77.2210.58)2 1.87.23 2.24ef l m =++⨯-⨯--⨯= 3、地基净反力j p 的计算。
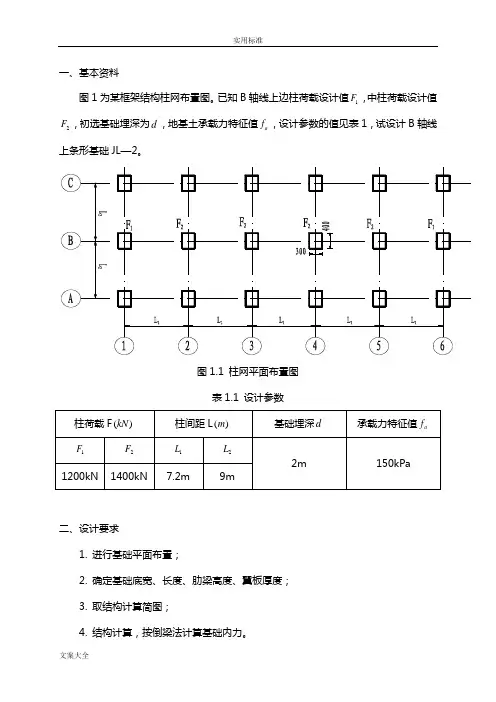
一、基本资料图1为某框架结构柱网布置图。
已知B 轴线上边柱荷载设计值1F ，中柱荷载设计值2F ，初选基础埋深为d ，地基土承载力特征值a f ，设计参数的值见表1，试设计B 轴线上条形基础JL —2。
图1.1 柱网平面布置图 表1.1 设计参数二、设计要求1. 进行基础平面布置；2. 确定基础底宽、长度、肋梁高度、翼板厚度；3. 取结构计算简图；4. 结构计算，按倒梁法计算基础内力。
5、根据内力进行配筋。
三、设计计算书1. 基础平面布置图根据题目条件及表中数据，绘制基础平面布置图，如图3.1.1所示图3.1.12. 基础底面尺寸（1）确定荷载合力重心位置设合力作用点与边柱A 的距离为c x ，根据合力距定理，以A 为参照点，有：14007.2140014.4140021.6140028.8120036181400412002ik ic ikF x x m F⨯+⨯+⨯+⨯+⨯===⨯+⨯∑∑（2）确定基础梁的长度和外伸尺寸基础梁两端外伸长度为12a a 、，取边跨的0.25倍。
取10.257.2 1.8a m =⨯=12()2(18 1.8)39.6c L x a m =+=⨯+= 239.6 1.87.25 1.8a m =--⨯=（3）按地基持力层的承载力确定基础梁的宽度b14004120021.83 1.8(20)39.6(150202)kFb m m L f d ⨯+⨯===≈-⨯-⨯∑（4）确定肋梁高度及翼板高度采用C30混凝土，21.43/t f N mm = 基底沿宽度b 方向的净反力28000112.2/1.839.6kn Fp kN m bL===⨯∑悬臂根部剪力设计值0.4 1.8()112.2(0.2)78.54/222n b V p kN m =-=⨯-=翼缘板有效高度0378.541078.560.70.71 1.43101h t V h mm f l β⨯≥==⨯⨯⨯⨯ 取0220h mm =（等厚翼板）。
柱下条形基础计算例题摘要：一、柱下条形基础计算概述二、柱下条形基础计算方法1.了解基本概念和参数2.计算条形基础的面积3.计算条形基础的承载力4.确定基础的材料和尺寸5.校核基础的稳定性三、实例分析四、注意事项五、总结正文：一、柱下条形基础计算概述柱下条形基础计算是建筑工程中基础设计的重要环节，它涉及到建筑物的稳定性和安全性。
在进行柱下条形基础计算时，需要充分了解和掌握相关概念和参数，以确保计算结果的准确性。
二、柱下条形基础计算方法1.了解基本概念和参数在进行柱下条形基础计算前，首先要了解以下基本概念和参数：（1）柱下条形基础：是指在柱子下方设置的一种基础形式，通常用于减轻柱脚的应力集中，提高基础的整体稳定性。
（2）基础底面积：是指条形基础底部的水平投影面积，用于计算基础的承载力和稳定性。
（3）基础高度：是指从基础底面到基础顶面的垂直距离。
（4）材料参数：包括基础材料的弹性模量、泊松比等。
2.计算条形基础的面积根据设计要求和工程地质条件，确定条形基础的形状和尺寸，然后计算基础的底面积。
3.计算条形基础的承载力根据基础的材料、尺寸和地质条件，采用合适的方法计算基础的承载力。
常见的方法有经验公式法、理论解析法和数值模拟法等。
4.确定基础的材料和尺寸根据计算得到的承载力和设计要求，选择合适的基础材料（如混凝土、砖石等），并确定基础的尺寸（如宽度、高度等）。
5.校核基础的稳定性根据国家相关规范和设计要求，校核基础的稳定性，主要包括抗压稳定性、抗拉稳定性、抗弯稳定性等。
三、实例分析以下为一个柱下条形基础计算的实例：假设某建筑工程，柱子直径为400mm，基础底座宽度为600mm，基础高度为800mm，土壤极限承载力为200kN/m。
现采用C30混凝土作为基础材料，试计算柱下条形基础的尺寸和稳定性。
根据实例，可以进行如下计算：1.计算基础底面积：600mm × 800mm = 480000 mm = 0.48 m2.计算基础承载力：200 kN/m × 0.48 m = 96 k N3.计算基础抗压稳定性：根据C30混凝土的抗压强度f"c = 20 MPa，抗压极限强度σ Lim = f"c × A = 20 MPa × 0.48 m = 96000 Pa4.校核基础稳定性：根据国家规范，基础稳定性安全系数不得小于1.5。
柱下条形基础计算例题
柱下条形基础计算是指在土木工程中，计算柱下条形基础的设
计和施工过程。
下面是一个柱下条形基础计算的例题：
假设我们要设计一个柱下条形基础，柱子的尺寸为1米×1米，深度为2米。
地下的土壤层为黏土，抗剪强度为150 kPa，承载力
为200 kPa。
现在我们需要计算基础的尺寸和承载力。
首先，我们需要计算基础的尺寸。
柱下条形基础的尺寸通常由
基础底面积和基础深度决定。
在这个例子中，基础底面积为1米×1米，基础深度为2米，所以基础的体积为1米×1米×2米=2立方米。
接下来，我们需要计算基础的承载力。
柱下条形基础的承载力
通常由土壤的承载力和基础底面积决定。
在这个例子中，土壤的承
载力为200 kPa，基础底面积为1米×1米，所以基础的承载力为
200 kPa × 1米× 1米 = 200 kN。
除了计算基础的尺寸和承载力，还需要考虑其他因素，如基础
的稳定性和安全性。
在设计柱下条形基础时，需要考虑土壤的性质、
地下水位、地震力等因素，并采取相应的措施来确保基础的稳定性和安全性。
总结起来，柱下条形基础计算涉及基础尺寸和承载力的计算，并需要考虑其他因素来确保基础的稳定性和安全性。
以上是一个柱下条形基础计算的例题。
建筑结构常规设计方法结构体系的力学模型上部结构设计：用固定支座代替基础，假设支座没有任何变形，求的结构的内力和支座反力。
基础设计：把支座反力作用于基础，用材料力学的方法求得地基反力，再进行基础得内力和变形验算。
地基验算：把基础反力作用于地基，验算地基的承载力和沉降。
常规设计得结果：上部底层和边跨的实际内力大于计算值，而基础的实际内力要比计算值小很多。
2 相对刚度影响（上部结构+基础）与地基之间的刚度比结构绝对柔性：相对刚度为0，产生整体弯曲，排架结构结构绝对刚性:相对刚度为无穷大，产生局部弯曲，剪力墙、筒体结构结构相对刚性：相对刚度为有限值，既产生整体弯曲，又产生局部弯曲, 砌体结构、钢筋混凝土框架结构(敏感性结构 )3 工程处理中的规定: ①按照具体条件不考虑或计算整体弯距时，必须采取措施同时满足整体弯曲的受力要求。
②从结构布置上，限制梁板基础（或称连续基础）在边柱或边墙以外的挑出尺寸，以减轻整体弯曲效应。
③在确定地基反力图形时，除箱形基础按实测以外，柱下条形基础和筏形基础纵向两端起向内一定范围，如1-2开间，将平均反力加大10%～20%设计。
④基础梁板的受力钢筋至少应部分通长配置（具体数量见有关规范），在合理的条件下，通长钢筋以多为好，尤其是顶面抵抗跨中弯曲的受拉钢筋，对筏板基础，这种钢筋应全部通长配置为宜7.8.2 柱下刚进混凝土条形基础的设计地基模型地基模型：用以描述地基σ～ε的数学模型. 下面介绍的地基模型应注意其适用条件。
1 文克尔地基模型基本假定：地基上任一点所受的压力强度与该点的地基沉陷s成正比，关系式如下:P=ksk—地基基床系数，表示产生单位变形所需的压力强度(kN／m3)；p—地基上任—点所受的压力强度(kPa)；s— p作用位置上的地基变形(m)。
注：基床系数k可根据不同地基分别采用现场荷载试验、室内三轴试验或室内固结试验成果获得。
见下表。
适用条件：抗剪强度很低的半液态土(如淤泥、软粘土等)地基或塑性区相对较大土层上的柔性基础;厚度度不超过梁或板的短边宽度之半的薄压缩层地基(如薄的破碎岩层)上的柔性基础.这个假定是文克勒于1867年提出的．故称文克勒地基模型。
该模型计算简便，只要k值选择得当，可获得较为满意的结果。
地基土越软弱，土的抗剪强度越低，该模型就越接近实际情况。
缺点：文克勒地基模型忽略了地基中的剪应力，按这一模型，地基变形只发生在基底范围内，而基底范围外2半无限弹性体法基本假定：假定地基土半无限弹性体，柱下条形基础看作时放在半无限弹性体上的梁，当荷载作用与半无限弹性体上时，某点的沉降不但和该点上的压力有关，和该点附近作用的荷载也有关。
特点：考虑了应力扩散，但扩散范围超出实际，未考虑地基的非均匀性。
适用条件：压缩层深度较大的一般土层的柔性基础。
要求土的弹性模量和泊松比角准确。
柱下条形基础设计1 构造要求2 内力计算方法简化的内力计算方法 （按线形分布的基底净反力）方法种类：倒梁法、剪力平衡法（1）倒梁法1）基本假定：a 、刚度较大，基础的弯曲挠度不致改变地基反力；b 、地基反力分布呈直线，其重心与作用于板上的荷载合力作用线重合。
2）适用条件：地基较均匀，上部结构刚度较好，荷载分布较均匀，且条形基础梁的高度大于1/6柱距（设计时尽可能按此设计），地基反力按直线分布，条形基础梁的内力可按连续梁计算，此时边跨跨中弯距及第一支座的弯距值乘以1.2系数。
补充：倒梁法计算假定1.将地基净反力作为基础梁的荷载，柱子看成铰支座，基础梁看成倒置的连续梁；2.作用在基础梁上的荷载为直线分布；3.竖向荷载合力作用点必须与基础梁形心相重合，若不能满足，两者偏心距以不超过基础梁长的3%为宜；4.结构和荷载对称时，或合力作用点与基础形心相重合时，地基反力为均匀分布；3）计算步骤①绘出条形基础的计算草图，包括荷载、尺寸等；②求合力作用点的位置 (目的是尽可能的将偏心地基净反力化成均匀的地基反力，然后确定基础梁的长度)。
设合力作用点离边柱的距离为Xc ，用合力矩定理，以A 点为参考点，则有：③确定基础梁的底面尺寸L,B 当Xc 确定后，按合力作用点与底面心形相重合的原则，可定出基础的长度L 。
确定后，宽度B 按地基承载力fa 确定 中心受荷 ：偏心受荷 ：n n i i w w i 1i 1M M T H G e ===+⋅+⋅∑∑∑④基础底板净反力计算n n n n i i i i i i i 1i 1i 1i 1c n ii 1N a M N a M x R N =====⋅+⋅+==∑∑∑∑∑n i W i 1k aN G G p f L B =++=≤⋅∑n i W i 1k an i WN G G p f L B N G G 6M =++=≤⋅++∑∑∑⑤确定基础梁的底板厚度h 及配筋则有：⑥求基础梁纵向正截面强度计算斜截面强度计算对连续梁可用弯矩分配法或连续梁系数法求解。
由于柱下条基一般两端都有外伸部分，因此，若用连续梁系数法，要对悬臂端进行处理，现有两种方法：1）悬臂端在净反力作用下的弯矩全部由悬臂端承担，不再传给其他支座，其他跨按连续梁系数法计算；2）悬臂端弯矩对其他跨有影响，此弯矩要传给其他支座，因此，悬臂端用弯矩分配法求出各支座及跨中弯矩，其他跨用连续梁系数法求出各支座及跨中弯矩，然后将所得结果叠加，或全梁用弯矩分配法求出各支座及跨中弯矩。
注意：按倒梁法求得的梁的支座反力，往往会不等于柱传来的竖向荷载（轴力）。
此时，可采用所谓“基底反力局部调整法”，即：将支座处的不平衡力均匀分布在本支座两侧各1/3跨度范围内，从而将地基反力调整为台阶状，再按倒梁法计算出内力后与原算得的内力叠加。
经调整后的不平衡力将明显减少，一般调整1～2次即可。
据基础梁的M 图，对各支座、跨中分别按矩形、T 形截面进行强度计算；据V 图，进行斜截面抗剪强度计算，并应满足构造要求（2）剪力平衡法（静定分析法）适用范围：上部结构为柔性结构，且自身刚度较大的条形基础以及联合基础。
计算方法：静力平衡条件（剪力平衡）计算出任意截面上的弯距 M 和剪力 V 。
【例】试确定如下图所示条形基础的底面尺寸，并用简化计算方法分析内力。
已知：基础埋深d=1.5m,地基承载力特征值fa=120Kpa,其余数据见图示。
【解】1、确定基础底面尺寸各柱竖向力的合力，距图中A 点的距离x 为 考虑构造需要，基础伸出A 点外取b=2.5m 。
2、内力分析：（1）倒梁法因荷载的合力通过基底形心，故地基反力是均布的，沿基础每米长度上的净反力值以柱底A 、B 、C 、D 为支座，按弯距分配法分析三跨连续梁，其弯距M 和剪力V 见图7-43b 。
（2）剪力平衡法按静力平衡条件计算内力：AB 跨内最大负弯距的截面至A 点的距离:则： 其余各截面的M 、V 均仿此计算，结果见图7-43c 。
0h t S 0y V h 0.7f M A 0.9h f ≥β≥96014.71754 1.21740 4.2x 7.85m 96017541740554⨯+⨯+⨯==+++,5.01m x =(96017541740554)/16.7300/n q KN m=+++=21M 3000.538KN m 2=⨯⨯=∙15540.5 1.35300a m =-=比较两种方法的计算结果，按剪力平衡法算出的支座弯距较大；按倒梁法算得的跨中弯距较大。
倒梁法剪力平衡法【书例7-12】如图7-44为某柱网布置图。
已知B 轴线上边柱荷载设计值中柱初选基础埋深为1.5m ，地基承载力特征值fa=120Kpa ，试设计B 轴线上条形基础。
【解】1、确定基底面积基础两边各放出：基础底宽度（综合荷载分项系数取1.35）： 取b=2.50m 设计。
2、梁的弯矩计算在对称荷载作用下，由于基础底面反力为均匀分布，因此单位长度地基的净反力为：基础梁可看成在均布线荷载 qn 作用下以柱为支座的五跨等跨度连续梁。
为了计算方便，可将图7-45a 分解为图7-45b 和图7-45c 两部分。
图7-45b 用力矩分配法计算，A 截面处的固端弯矩为：在图7-45c 的荷载作用下，利用五跨等跨度连续梁的相应弯矩系数m ，可得有关截面的弯矩：支座B （和B ＇）：其余同（略）。
将图7-45b 与c 的弯矩叠加，即为按倒梁法计算所得的JL —2梁的弯矩图[见图7-45d].3、梁的剪力计算基础梁TL —2的剪力图绘于图7-45e 。
4、梁板部分计算基底宽2500㎜，主助宽500㎜（400+2×50），翼板外挑长度 1/2 ×（2500-500）=1000㎜，翼板外边缘厚度200㎜，梁助处（相当于翼板固定端）翼板厚度300㎜（见图7-46）。
翼板采用C20混凝土，HPB235钢筋。
基底净反力设计值： (1)斜截面抗剪强度验算（按每米长计）实际 >113.2㎜，可以。
m l 2363==[]/1.351310410802 2.48(20)(6522)(12020 1.5) 1.35a Fb m l f d ⨯+⨯≥==-⨯+⨯⨯-⨯⨯∑21887.22.5n n q p kPa b ===087.2113.20.70.7 1.0 1.10h a V h mm f β===⨯⨯300401025020oh mm mm =--=（假定受力筋直径为，有垫层）】（2）翼板受力筋计算配 实际AS =942mm²)。
5、肋梁部分计算肋梁高取 宽500㎜。
主筋用HRB335钢筋，C20混凝土。
（1）正截面强度计算根据图7-45d 的JL-2梁M 图，对各支座、跨中分别按矩形、T 形截面进行正截面强度计算。
轴②支座处（M=700KNm ）由 查混凝土设计手册可知 （2）斜截面强度计算轴②左边截面（V=698KN ）：配 箍筋（四肢箍）。
，可以各部分的正、斜截面配筋均可列表计算，此略。
统一调整后，JL-2梁的配筋见图7-46。
62043.610923/0.90.9250310s y M A mm m h f ⨯===⨯⨯60001000,66l mm ==622070010 1.55500950M A bh ⨯===⨯%54.0=ρ1408000.70.7 1.10500950350950h t f h KN β⎛⎫=⨯⨯⨯⨯= ⎪⎝⎭。
