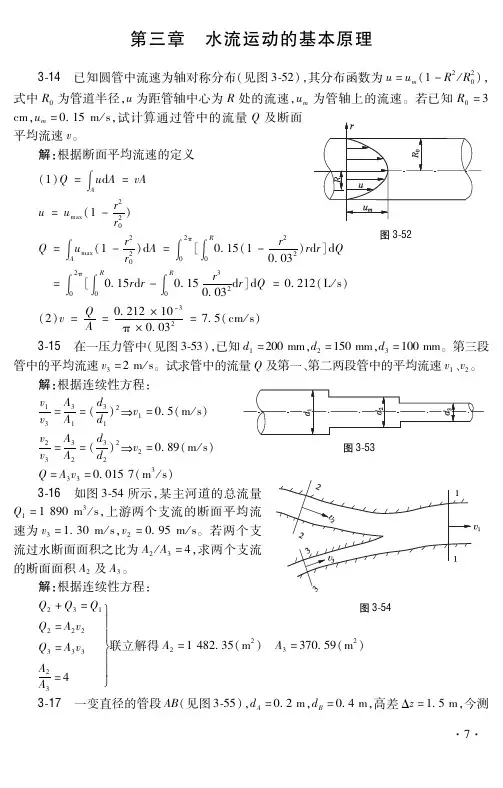
第三章水流运动的基本原理上一章已阐述了有关水静力学的基本概念、基本理论及其应用。
但在自然界或许多工程实际问题中，液体多处于运动状态。
只有对运动状态的液体进行深入地分析研究才能得出液体运动规律的一般原理。
因此，从本章开始将转入有关水流运动问题的讨论。
实际工程中的水流尽管千差万别，变化万千，但理论和实践都证明，它们必须遵循物质机械运动的普遍规律，如在物理学或理论力学中已学习过的质量守恒定律、动能定理和动量定理等。
本章作为水流运动问题的开端，重点介绍描述液体运动的方法和有关水流运动的基本概念，讨论并建立一元恒定流的连续性方程、能量方程、动量方程和动量矩方程。
至于如何应用这些规律解决具体边界条件特定形式的水流运动，如管流、明渠水流、堰闸水流等将在以后各章中分别讨论。
本章是水力学的理论核心内容，它将为以后各章的学习打下良好的基础。
第一节描述水流运动的两种方法一、描述水流运动的两种方法水流运动时，表征液体运动的各种物理量称为运动要素，常遇到的运动要素有流速、压强、加速度、切应力、液体的密度和容重等。
这些运动要素随着时间和空间位置不断发生变化。
水力学中研究水流运动通常采用两种方法，即迹线法和流线法。
（一）迹线法迹线法又叫拉格朗日（Lagrange）法，就是像物理学中研究固体运动那样，把液体中单个质点作为研究对象，通过对每个水流质点运动轨迹的研究来获得整个液体运动的规律。
运用迹线法研究液体运动实质上与研究一般固体力学方法相同，所以也称为质点系法。
（二）流线法流线法又叫欧拉（Euler）法，就是把充满液体质点的固定空间作为研究对象，不再跟踪每个质点，而是把注意力集中在考察分析水流中的水质点在通过固定空间点时的运动要素的变化情况，来获得整个液体运动的规律。
水流运动时在同一时刻每个质点都占据一个空间点，只要搞清楚每个空间点上运动要素随时间的变化规律，就可以了解整个水流的运动规律了。
由于流线法是以流动的空间作为研究对象，而且通常把液体流动所占据的空间称为流场。
