矩阵微分方程

矩阵论第七章函数矩阵与矩阵微分方程北京理工大学高数教研室* 第一章第一节函数第七章函数矩阵与矩阵微分方程函数矩阵定义: 以实变量的函数为元素的矩阵称为函数矩阵, 其中所有的元素都是定义在闭区间上的实函数。

函数矩阵与数字矩阵一样也有加法, 数乘, 乘法, 转置等几种运算, 并且运算法则完全相同。

例:已知计算定义:设为一个阶函数矩阵, 如果存在阶函数矩阵使得对于任何都有那么我们称在区间是可逆的。

称是的逆矩阵, 一般记为例 :已知那么在区间上是可逆的, 其逆为函数矩阵可逆的充分必要条件定理 : 阶矩阵在区间上可逆的充分必要条件是在上处处不为零, 并且其中为矩阵的伴随矩阵。

定义:区间上的型矩阵函数不恒等于零的子式的最高阶数称为的秩。

特别地, 设为区间上的阶矩阵函数, 如果的秩为 , 则称一个满秩矩阵。

注意:对于阶矩阵函数而言, 满秩与可逆不是等价的。

即:可逆的一定是满秩的, 但是满秩的却不一定是可逆的。

例 :已知那么。

于是在任何区间上的秩都是2。

即是满秩的。

但是在上是否可逆, 完全依赖于的取值。

当区间包含有原点时, 在上有零点, 从而是不可逆的。

函数矩阵对纯量的导数和积分定义:如果的所有各元素在处有极限, 即其中为固定常数。

则称在处有极限, 且记为其中如果的各元素在处连续, 即则称在处连续, 且记为其中容易验证下面的等式是成立的: 设则定义:如果的所有各元素在点处(或在区间上)可导, 便称此函数矩阵在点处(或在区间上)可导, 并且记为函数矩阵的导数运算有下列性质: 是常数矩阵的充分必要条件是设均可导, 则设是的纯量函数, 是函数矩阵,与均可导, 则特别地, 当是常数时有 (4) 设均可导, 且与是可乘的, 则因为矩阵没有交换律,所以 (5) 如果与均可导, 则 (6) 设为矩阵函数, 是的纯量函数, 与均可导, 则定义: 如果函数矩阵的所有各元素在上可积, 则称在上可积, 且函数矩阵的定积分具有如下性质: 例1 :已知函数矩阵试计算证明: 由于 , 所以下面求。

常数矩阵微分方程基解矩阵的计算方法常数矩阵微分方程基解矩阵是指对于一个m阶常系数矩阵微分方程组x′(x)=xx(x)，其中x(x)为x的函数，x为常数矩阵，基解矩阵是一组线性无关的解所构成的矩阵。

计算常数矩阵微分方程基解矩阵的方法主要有以下几种：常数变易法、指数矩阵法、特征值法。

一、常数变易法
使用常数变易法求解常数矩阵微分方程基解矩阵的步骤如下：
1.假设基解矩阵为x(x)，则存在常数矩阵x，使得
x(x)=xx^xx。

2.对基解矩阵进行求导，并代入微分方程，得到
xxx(x)(x)=xx(x)，其中x(x)(x)表示第n阶导数。

3.解出x(x)(x)，得到x的表达式。

4.代入x=0时的初始条件，求解得到x的具体值。

5.将x代入基解矩阵的表达式中，得到基解矩阵。

二、指数矩阵法
使用指数矩阵法求解常数矩阵微分方程基解矩阵的步骤如下：
1.求解常数矩阵x的特征值和特征向量。

2.将特征值分别代入指数函数的表达式中，得到特征向量的指数函数形式。

3.将特征向量的指数函数形式构成的矩阵x和其逆矩阵x^(-1)代入基解矩阵的表达式中，得到基解矩阵。

三、特征值法
使用特征值法求解常数矩阵微分方程基解矩阵的步骤如下：
1.求解常数矩阵x的特征值和特征向量。

2.将特征向量的形式代入基解矩阵的表达式中，得到基解矩阵。

在实际计算中，选择哪种方法取决于方程的形式、矩阵的性质和计算的复杂程度。

以上三种方法均可得到常数矩阵微分方程的基解矩阵，计算方法相对较为简单，但对于高阶矩阵微分方程，计算工作量可能较大，需要根据具体情况选择合适的方法。

线性代数矩阵的分解与微分方程应用线性代数是数学中的一个重要分支，它研究的是线性空间以及其上的线性变换。

线性代数在不同领域中都有广泛的应用，比如说在计算机图形学、物理学、经济学等领域中都起着非常重要的作用。

其中，矩阵的分解和微分方程的应用是线性代数的两大重要内容。

一、矩阵的分解矩阵的定义是一个由数字排成的矩形表格。

在线性代数中，矩阵是一个重要的工具，矩阵的分解是矩阵理论中的一个基本问题。

矩阵的分解通常是指将一个矩阵分解成几个特定形式的矩阵的乘积。

常见的矩阵分解包括LU分解、QR分解、SVD分解等。

1、LU分解LU分解是线性代数中的一种矩阵分解方法，可以将一个矩阵分解成一个下三角矩阵L和一个上三角矩阵U的乘积。

LU分解可以用于求解线性方程组、求矩阵的逆以及计算矩阵的行列式等问题。

在实际应用中，使用LU分解求解线性方程组比直接求解更加高效和准确。

2、QR分解QR分解是一个将一个矩阵分解成一个正交矩阵Q和一个上三角矩阵R的乘积的方法。

QR分解在求解最小二乘问题、特征值问题以及解非线性方程组等问题中都有广泛的应用。

3、SVD分解SVD分解是一种将一个矩阵分解成三个矩阵的乘积的方法，包括一个左奇异矩阵、一个右奇异矩阵和一个奇异值矩阵。

SVD分解可以用于降维、信号处理、图像处理等方面。

二、微分方程的应用微分方程是研究变化的数学分支，它研究的是变量与其变化率的关系。

微分方程在科学、工程和经济等领域中都有广泛的应用。

微分方程的解法中涵盖了矩阵分解的知识。

1、矩阵微分方程矩阵微分方程指的是方程中包含了一个矩阵与它的导数。

矩阵微分方程在控制系统、差分方程的研究中都有广泛的应用。

解矩阵微分方程时，可以使用矩阵指数函数或拉普拉斯变换等方法。

2、级数解法级数解法是一种用级数求微分方程解的方法。

在级数解法中，将未知函数表示为级数的形式，将其代入微分方程中，然后通过逐项比较系数来求解微分方程。

级数解法在近似计算和数值解法方面都有重要应用。

方向余弦矩阵的微分方程求解方向余弦矩阵是描述刚体在空间中姿态变化的重要工具，它可以将刚体的旋转转化为矩阵运算。

在机器人学、航空航天等领域中，方向余弦矩阵的微分方程求解对于姿态控制和导航非常关键。

姿态是刚体相对于参考坐标系的方向，它可以由方向余弦矩阵表示。

方向余弦矩阵是一个3×3的矩阵，其中的元素描述了刚体在空间中的旋转关系。

我们假设刚体的初始姿态为单位阵，即方向余弦矩阵为单位矩阵。

刚体的姿态变化可以由方向余弦矩阵的微分方程描述。

假设刚体在空间中绕着某个轴进行旋转，我们可以通过微分方程来求解方向余弦矩阵的变化。

我们定义一个表示刚体角速度的向量ω，在刚体坐标系下表示为[ωx, ωy, ωz]，其中ωx、ωy、ωz分别表示绕x轴、y轴、z轴的角速度。

刚体的角速度向量可以通过方向余弦矩阵与角速度在参考坐标系下的表示之间的关系计算得到。

然后，我们可以得到方向余弦矩阵的微分方程：dC/dt = Cω_hat其中，dC/dt表示方向余弦矩阵的微分，C表示方向余弦矩阵，ω_hat表示角速度向量的斜对称矩阵。

方向余弦矩阵的微分方程描述了刚体姿态的变化速率与角速度的关系。

通过求解方向余弦矩阵的微分方程，我们可以得到刚体姿态的变化规律。

在实际应用中，可以利用数值求解方法，如欧拉法、龙格-库塔法等，来求解微分方程的数值解。

方向余弦矩阵的微分方程求解对于姿态控制和导航具有重要意义。

它可以帮助我们理解刚体在空间中的旋转规律，并为机器人、航空器等的姿态控制提供基础。

对于航天器的导航来说，方向余弦矩阵的微分方程求解可以帮助我们准确地预测航天器的姿态变化，从而实现精确的导航和定位。

方向余弦矩阵的微分方程求解是研究刚体姿态变化的重要内容。

通过求解微分方程，可以揭示刚体姿态的变化规律，并为姿态控制和导航提供理论支持。

在实际应用中，我们可以利用数值求解方法来求解微分方程，从而实现对刚体姿态的精确控制和导航。

矩阵微积分基础知识矩阵微积分是微积分的一个重要分支，它将微积分的概念和方法应用于矩阵和向量的运算中。

在矩阵微积分中，我们可以通过对矩阵进行微分和积分来研究矩阵的性质和变化规律。

本文将介绍矩阵微积分的基础知识，包括矩阵的导数、矩阵的积分和矩阵微分方程等内容。

一、矩阵的导数在矩阵微积分中，我们可以定义矩阵的导数。

对于一个矩阵函数f(X)，其中X是一个矩阵，我们可以通过对f(X)的每个元素分别求导来得到矩阵的导数。

具体而言，如果f(X)的每个元素都是可导的，那么矩阵f(X)的导数就是一个与f(X)具有相同维度的矩阵，其中每个元素都是对应元素的导数。

例如，对于一个2×2的矩阵X = [x1 x2; x3 x4]，我们可以定义一个矩阵函数f(X) = [x1^2 x2^2; x3^2 x4^2]。

那么矩阵f(X)的导数就是一个2×2的矩阵，其中每个元素都是对应元素的导数，即f'(X) = [2x1 2x2; 2x3 2x4]。

二、矩阵的积分与矩阵的导数类似，我们也可以定义矩阵的积分。

对于一个矩阵函数f(X)，其中X是一个矩阵，我们可以通过对f(X)的每个元素分别积分来得到矩阵的积分。

具体而言，如果f(X)的每个元素都是可积的，那么矩阵f(X)的积分就是一个与f(X)具有相同维度的矩阵，其中每个元素都是对应元素的积分。

例如，对于一个2×2的矩阵X = [x1 x2; x3 x4]，我们可以定义一个矩阵函数f(X) = [∫x1dx1 ∫x2dx2; ∫x3dx3 ∫x4dx4]。

那么矩阵f(X)的积分就是一个2×2的矩阵，其中每个元素都是对应元素的积分，即∫f(X)dX = [∫x1dx1 ∫x2dx2; ∫x3dx3 ∫x4dx4]。

三、矩阵微分方程矩阵微分方程是矩阵微积分中的一个重要概念。

它是描述矩阵函数与其导数之间关系的方程。

一般而言，矩阵微分方程可以分为常微分方程和偏微分方程两种类型。

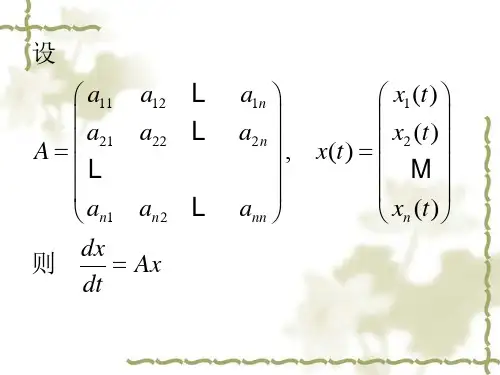
第九讲矩阵微分方程一、矩阵的微分和积分1.矩阵导数定义：若矩阵ij m ×n A(t)=(a (t))的每一个元素a (t)ij 是变量t 的可微函数，则称A(t)可微，其导数定义为'ij m ×n da dA=A (t)=()dt dt由此出发，函数可以定义高阶导数，类似地，又可以定义偏导数。

2.矩阵导数性质：若A(t),B(t)是两个可进行相应运算的可微矩阵，则（1）d dA dB[A(t)±B(t)]=±dt dt dt（2）d dA dB [A(t)B(t)]=B +A dt dt dt （3）d da dA[a(t)A(t)]=A +a dt dt dt （4）()()()()()()()t A t A t Ad dde =A e =e Ac o s t A =-A s i n t A s i n t A =A c o s t Ad td t d t(A 与t 无关)此处仅对tA tA tAd (e )=Ae =e A dt加以证明证： tA 2233223d d 111(e )=(I+tA +t A +t A +)=A +tA +t A +dt dt 2!3!2!22tA1=A(I+tA+t A +)=Ae 2!又22tA 1=(I+tA+t A +)A=e A 2!3.矩阵积分定义：若矩阵A(t)=(a (t))m ×n ij的每个元素ij a (t)都是区间01[t ,t ]上的可积函数，则称A(t)在区间01[t ,t ]上可积，并定义A(t)在01[t ,t ]上的积分为⎛⎫⎰⎰ ⎪⎝⎭1100ij t t A(t)dt =a (t)dt t t m ×n4.矩阵积分性质（1）⎰⎰⎰111t t t t t t [A(t)±B(t)]dt =A(t)dt±B(t)dt（2）⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎰⎰⎰⎰11110000t t t t t t t t [A(t)B]dt =A (t)dt B,[AB(t)]dt =A B(t)dt （3）'''⎰⎰t ba adA(t )dt =A(t),A (t)dt =A(b)-A(a)dt 二、阶线性齐次常系数常微分方程组设有一阶线性其次常系数常微分方程组⎧⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩ 11111221n n 22112222n n n n11n22nn ndx =a x(t)+a x (t)++a x (t)dt dx =a x(t)+a x (t)++a x (t)dt dx =a x(t)+a x (t)++a x (t)dt式中t 是自变量，i ix =x(t)是t 的一元函数 ij (i=1,2,,n),a (i,j=1,2,,n)是常系数。

一类二阶矩阵微分方程的特解矩阵的微分方程是一类相对复杂的微分方程，也是近年来非常热门的研究课题。

矩阵的微分方程的特解是指满足特定条件的特殊解，弗拉瓦尔（F. L. Varvarin）等人针对这类矩阵微分方程，提出了一类具有重要意义的特解：一类二阶矩阵微分方程的特解。

弗拉瓦尔等人提出的“一类二阶矩阵微分方程”是指一个对称矩阵$A$的微分方程。

记其特解为$x(t)$，则有：$ frac{mathrm{d}^{2} x(t)}{mathrm{d} t^{2}} + A x(t) = 0 $这类特解的求解方法是：首先将$A$分解成特征值-特征向量形式：$ A = Q Lambda Q^{T} $，其中$Q=left(q_{1}, q_{2}, ldots,q_{n}right)$为正交矩阵，$Lambda = left(lambda_{1}, lambda_{2}, ldots, lambda_{n}right)$为其特征值对角矩阵，即$A$的特征分解。

然后将$x(t)$替换为$Qoverline{x}$，其中$overline{x}$为一个$n$维列向量，称为$A$的共轭向量，则上式变为：$ frac{mathrm{d}^{2} overline{x}}{mathrm{d} t^{2}} + Lambda overline{x} = 0 $上式具有$n$个解$overline{x_{j}} = left(c_{j} costheta_{j}+s_{j} sin theta_{j}right) e^{lambda_{j} t} quad(j=1,2, ldots, n)$，其中$c_{j}, s_{j}$和$theta_{j}$为常数，$lambda_{j}$为$A$的特征值，于是，原微分方程的特解可以表示为： $x(t)=Q left(sum_{j=1}^{n}left(c_{j} cos theta_{j}+s_{j}sin theta_{j}right) e^{lambda_{j} t}right)$弗拉瓦尔等人对于这类特解进行了进一步研究，他们指出，若特征值$lambda_{j}=0$，即$A$具有零特征值，则上式变为：$x(t) = Q left(sum_{j=1}^{n} left(c_{j}t+s_{j}right)right)$这表明，当$A$具有零特征值时，特解可以表示为$A$的共轭向量的有限次多项式。

矩阵常微分方程求解矩阵常微分方程是指形式为$\frac{{dX}}{{dt}}=AX$的方程，其中$X$是一个$n\times 1$的矩阵，$A$是一个$n\times n$的常数矩阵。

要求解矩阵常微分方程，可以使用矩阵的特征值和特征向量来求解。

首先，求解特征值问题$AX=\lambda X$，其中$\lambda$是特征值，$X$是特征向量。

求解得到的特征值为$\lambda_1, \lambda_2, ..., \lambda_n$，对应的特征向量为$X_1, X_2, ..., X_n$。

然后，构造$n\times n$的矩阵$P$，其中每列是一个特征向量$X_i$，使得$P=[X_1, X_2, ...,X_n]$。

接下来，构造$n\times n$的对角矩阵$\Lambda$，其中对角线上的元素是特征值$\lambda_1,\lambda_2, ..., \lambda_n$。

最后，可以得到方程的通解$X(t)=P\Lambda e^{At}P^{-1}$，其中$e^{At}$是矩阵$A$的指数函数，$P^{-1}$是矩阵$P$的逆矩阵。

需要注意的是，指数函数$e^{At}$的计算需要使用矩阵的幂级数展开，即$e^{At}=\sum_{k=0}^{\infty} \frac{1}{k!}(At)^k$，其中$(At)^k$代表矩阵$At$的$k$次幂。

在实际求解时，可以利用计算工具如MATLAB或Python的NumPy库中的函数来求解矩阵常微分方程。

例如，在Python中可以使用scipy库中的`scipy.linalg.expm`函数来计算矩阵的指数函数，使用NumPy库中的`numpy.linalg.eig`函数来求解特征值和特征向量，使用NumPy库中的`numpy.linalg.inv`函数来计算矩阵的逆矩阵。

矩阵微分方程的解法引言矩阵微分方程是数学中的一个重要分支，它研究了矩阵的导数和微分方程之间的关系。

在许多领域，如物理学、工程学和经济学等，矩阵微分方程都扮演着重要的角色。

本文将探讨矩阵微分方程的解法，包括常微分方程和偏微分方程两种情况。

常微分方程的解法一阶常微分方程对于形如dydx=f(x,y)的一阶常微分方程，可以通过分离变量的方法求得解。

将方程变形为dy=f(x,y)dx，然后将变量分离得到dyf(x,y)=dx。

对两边同时积分，得到∫dyf(x,y)=∫dx+C，其中C为常数。

最后求解出y和x之间的关系。

二阶常微分方程对于形如d 2ydx2+p(x)dydx+q(x)y=g(x)的二阶常微分方程，可以通过特征根法或变化参数法求解。

特征根法假设方程的通解为y=y1(x)+y2(x)，其中y1(x)是对应于齐次方程d2ydx2+p(x)dydx+q(x)y=0的通解，y2(x)是一个特解。

通过特征根法可以求得齐次方程的通解y1(x)。

然后根据特解的形式，代入原方程得到特解y2(x)。

最后将齐次方程的通解和特解相加，即可得到原方程的通解。

变化参数法假设方程的一个特解为y=y1(x)，其中y1(x)是对应于齐次方程d2ydx2+p(x)dydx+q(x)y=0的通解。

通过变化参数法，可以求得齐次方程的通解y1(x)。

然后令y=u (x )y 1(x )，将u (x )看作是x 的函数，代入原方程并化简得到du dx =−g (x )y 1(x )W(y 1(x ))，其中W(y 1(x ))是y 1(x )的朗斯基行列式。

最后求解出u (x )，再将u (x )代入y =u (x )y 1(x )，即可得到原方程的特解。

偏微分方程的解法偏微分方程在数学的多个领域中都有广泛应用，包括物理、工程和经济学等。

下面介绍两种常见的偏微分方程的解法。

热传导方程的解法热传导方程是描述物体在热平衡状态下的热传导过程的方程。

矩阵求微分方程一、引言微分方程是数学中的重要分支之一，它描述了自然界中许多现象的变化规律。

矩阵求微分方程是解决微分方程的一种常见方法，它可以将微分方程转化为矩阵形式进行求解。

本文将介绍矩阵求微分方程的基本思路和具体步骤。

二、基本概念1. 线性微分方程线性微分方程指的是具有以下形式的微分方程：y' + p(t)y = q(t)其中p(t)和q(t)都是已知函数，y表示未知函数。

2. 矩阵矩阵是由数个数构成的矩形数组，其中每个数称为元素。

矩阵可以表示为：A = [a_ij]其中i表示行号，j表示列号，a_ij表示第i行第j列的元素。

3. 线性代数基础知识在进行矩阵求解时需要掌握线性代数基础知识，如矩阵加减、乘法、转置等运算规则。

三、矩阵求解步骤1. 将线性微分方程转化为向量形式将未知函数y及其导数y'看作向量，并将p(t)和q(t)看作常向量，则线性微分方程可以表示为：y' = Ay + b其中A是一个n阶矩阵，b是一个n维常向量。

2. 求解齐次线性微分方程将b置为零，即求解齐次线性微分方程：y' = Ay其通解可以表示为：y(t) = c_1e^(λ_1t)v_1 + c_2e^(λ_2t)v_2 + ... + c_ne^(λ_nt)v_n其中λ_i和v_i分别表示A的特征值和对应的特征向量，c_i是任意常数。

3. 求解非齐次线性微分方程将b不为零时的情况加入通解中，即可得到非齐次线性微分方程的通解：y(t) = y_h(t) + y_p(t)其中y_h(t)是齐次线性微分方程的通解，y_p(t)是非齐次线性微分方程的一个特解。

4. 求解特解求解非齐次线性微分方程的特解需要根据b的形式进行分类讨论。

一般情况下，可以采用常数变易法或待定系数法求解。

具体步骤如下：(1) 常数变易法设特解为y_p(t) = u(t)v，其中u(t)和v都是未知函数。

将y_p(t)代入非齐次线性微分方程中，并求解u(t)和v的值。

矩阵常微分方程及其解析应用随着科学技术不断发展，对于复杂系统的研究也越来越深入。

在这个过程中，矩阵常微分方程作为数学工具的应用也越来越广泛。

本文将对矩阵常微分方程及其解析应用做出简要介绍。

一、矩阵常微分方程的概念及意义矩阵常微分方程是指矩阵值函数满足常微分方程的情形，其中常微分方程指的是只依赖自变量的微分方程，而不依赖于另外的变量。

矩阵常微分方程在科学研究中被广泛运用，例如在物理、计算机等领域中，都能看到它的应用。

以物理领域为例，矩阵常微分方程提供了一种描述系统动力学的方法。

对于某一特定的系统，通过对其状态的研究，可以得到该系统中的基本动力学规律。

而矩阵常微分方程可以通过对这些规律加以整合和描述，提供一个更为全面和准确的模型，揭示系统内部的运动机制。

二、矩阵常微分方程的解析应用矩阵常微分方程的应用是十分广泛的，尤其是在控制理论、机器人学、动画制作等方面，得到了广泛的应用。

在控制理论中，矩阵常微分方程可以提供一种更加高效的控制算法。

例如，可以用矩阵常微分方程描述某一系统的状态，利用其模型进行控制，通过对系统内部模型的详细分析，可以设计出最优的控制方法，提高系统性能。

在机器人学中，矩阵常微分方程可以用来描述机器人的运动规律。

例如，对于具有多自由度的机器人，可以用矩阵常微分方程描述各个关节的运动状态，进而分析和优化机器人的动态性能，设计出满足操作要求的机器人运动规律。

在动画制作中，矩阵常微分方程可以应用于人物动作捕捉技术中。

在此过程中，人类动作的运动轨迹可以被表示为矩阵常微分方程的形式，可以利用该方程式来指导人物的运动轨迹，从而生成更加真实、自然的动画效果。

三、矩阵常微分方程求解方法矩阵常微分方程的求解方法有多种。

其中，最为常见的方法是基于矩阵的特征值与特征向量进行求解。

具体来说，可以利用矩阵对角化定理将矩阵常微分方程转化为一组关于矩阵特征值和特征向量的常微分方程组，进而求解出该矩阵常微分方程的解析解。

矩阵法求解微分方程组在数学的世界里，有一个神奇的地方，那就是微分方程组。

听上去就像个高深莫测的术语，对吧？其实这就像一场探险，特别是用矩阵法去解这些方程的时候，简直像打开了一个新世界。

想象一下，微分方程组就像一群小朋友在操场上追逐打闹，每个小朋友都有自己的个性和特点，他们有时候会一起玩，有时候又会分开。

但是一旦我们用矩阵这个大玩具把他们聚在一起，哇，事情就变得简单多了。

咱们得搞清楚什么是矩阵。

矩阵就像是一张表格，上面摆满了数字。

看上去有点复杂，其实它就像我们每天用的购物清单，只不过这里面装的不是苹果和香蕉，而是方程的系数。

对了，矩阵的每一行每一列都可以看作是微分方程组中的一个方程，简直是一目了然。

用矩阵把这些方程整理在一起，就像把那些小朋友们排成整齐的队伍，马上就显得有条理多了。

我们来聊聊如何用矩阵法求解这个微分方程组。

步骤其实不复杂。

把方程转化成矩阵的形式。

听上去好像是个数学魔法，其实就是把各个方程的系数和变量按照一定的规则摆在一起。

比如，假设你有两个方程，像“y' = 2x + 3”和“z' = 4y + 5”，那么就可以把它们整理成一个大矩阵。

这样，咱们就把问题浓缩成了一张图表，看着舒服多了。

矩阵法的“主角”就是特征值和特征向量。

说到特征值，那可是个大咖！它决定了整个系统的行为。

特征值就像是那些小朋友的性格，有的活泼好动，有的安静内敛。

不同的特征值会导致方程组的解有不同的表现，就像小朋友们的游戏风格，千奇百怪，各有特色。

通过计算特征值，我们可以了解到系统的长远趋势，是朝着繁荣昌盛的方向，还是走向凋零的边缘。

然后，咱们还得求解特征向量。

这个过程就像是在找合适的搭档，谁和谁在一起最默契。

特征向量能告诉我们，如何从特征值出发，找到具体的解。

也就是说，特征向量会为我们指明道路，让我们在解的海洋中找到方向。

通过这些特征值和特征向量的组合，我们就能把微分方程组的解找出来，真是令人惊喜！如果你觉得这些步骤听上去太复杂，不用担心，实际操作起来并没有想象中那么麻烦。

用矩阵函数方法求微分方程微分方程是自然科学和工程学科中经常遇到的问题，求解微分方程的方法有很多种，其中一种是使用矩阵函数的方法。

在这篇文章中，我们将介绍如何使用矩阵函数来求解微分方程，并通过一个具体的例子来说明此方法的应用。

矩阵函数的方法是一种求解常微分方程组的有效方法，它将微分方程组转化为矩阵的形式，然后通过对矩阵求解其特征值和特征向量来得到微分方程组的解。

首先，让我们考虑一个一阶线性微分方程组的例子：(1) dx/dt = Ax其中x是一个n维向量，A是一个n×n矩阵。

我们可以将该微分方程组表示为矩阵形式：(2) dX/dt = AX其中X是一个n×n矩阵，A是一个n×n矩阵。

为了求解这个微分方程组，我们首先将X和A分解为特征值和特征向量的形式：(3)A=PDP^-1其中D是一个对角矩阵，其对角线上的元素是矩阵A的特征值，P是一个矩阵，其列向量是矩阵A的特征向量。

将方程(3)代入方程(2)中，得到：(4) dX/dt = PDP^-1X我们令Y=P^-1X，那么方程(4)可以进一步转化为：(5) dY/dt = DY这是一个非常简单的微分方程组(6)Y(t)=e^(Dt)Y(0)其中e^(Dt)是一个对角矩阵，其对角线上的元素是特征值e^λt，Y(0)是初始条件。

最后，我们将Y(t)代入方程(5)得到X(t)：(7)X(t)=Pe^(Dt)Y(0)综上所述，我们使用矩阵函数的方法求解微分方程组的步骤如下：首先，将微分方程组表示为矩阵形式；然后，求解矩阵的特征值和特征向量；最后，将特征值和特征向量代入矩阵函数公式中求解微分方程组的解。

通过以上的介绍，我们可以看出矩阵函数的方法是一种求解微分方程组的非常有效的方法，它利用了矩阵的特征值和特征向量的性质来简化微分方程组的求解过程。

在实际应用中，我们可以通过计算机编程来实现矩阵函数的方法，以求解复杂的微分方程组。

总之，矩阵函数的方法是一种求解微分方程组的重要方法，它可以简化求解过程并得到准确的解。

矩阵微分方程的解法一般的矩阵微分方程可以写成如下形式：$$\frac{d\mathbf{Y}}{dt}=\mathbf{A}(t)\mathbf{Y}(t)+\mathbf {F}(t)$$其中$\mathbf{Y}(t)$是$n$维列向量，$\mathbf{A}(t)$是$n\times n$的矩阵，$\mathbf{F}(t)$是$n$维列向量。

解法如下：1. 求解齐次微分方程$$\frac{d\mathbf{Y}}{dt}=\mathbf{A}(t)\mathbf{Y}(t)$$先求得$\mathbf{A}(t)$的本征值和本征向量，设$\mathbf{X}(t)$是使得$\mathbf{A}(t)\mathbf{X}(t)=\lambda(t)\mathbf{X}(t)$成立的$n$维列向量，则通解为：$$\mathbf{Y}(t)=\sum_{i=1}^nc_i\mathbf{X}_i(t)e^{\int\lambda_i(t)dt}$$其中$c_i$是常数，$\mathbf{X}_i(t)$是满足$\mathbf{A}(t)\mathbf{X}_i(t)=\lambda_i(t)\mathbf{X}_i(t)$的归一化本征向量，$\lambda_i(t)$是本征值。

2. 求解非齐次微分方程将上一步的通解代入微分方程，得到：$$\sum_{i=1}^nc_i\left(\frac{d\mathbf{X}_i(t)}{dt}e^{\int\lambda_i(t)dt}+\mathbf{X}_i(t)e^{\int\lambda_i(t)dt}\lambda_i(t)\right)=\mathbf{F}(t)$$解得$c_i$，带入通解即可得到矩阵微分方程的解。

matlab求解矩阵微分方程矩阵微分方程是常见的数学模型，它描述了矩阵随时间的变化规律。

在实际应用中，矩阵微分方程广泛应用于控制系统、信号处理、图像处理等领域。

在本文中，我们将介绍如何使用matlab求解矩阵微分方程。

我们需要了解矩阵微分方程的基本形式。

矩阵微分方程可以表示为x'(t)=Ax(t)，其中x(t)是一个n维列向量，A是一个n×n矩阵。

它的解可以表示为x(t)=exp(At)x0，其中x0是初始向量。

在matlab中，我们可以使用ode45函数来求解矩阵微分方程。

ode45是matlab中的一个常用ODE求解器，可以求解一般的非刚性ODE。

它的基本用法是ode45(odefun,tspan,y0)，其中odefun是一个函数句柄，tspan是时间区间，y0是初始向量。

为了使用ode45求解矩阵微分方程，我们需要将其转化为向量微分方程。

具体来说，我们可以将x(t)展开为一个列向量，然后将矩阵微分方程转化为向量微分方程y'(t)=f(t,y(t))，其中y(t)是一个n²维列向量，f(t,y(t))是一个n²维列向量的函数。

具体地，我们可以将矩阵A展开为一个n²维列向量，然后将x(t)展开为一个n维列向量，从而得到向量微分方程y'(t)=Ay(t)，其中y(t)是一个n²维列向量。

接下来，我们可以定义一个函数handle来表示向量微分方程f(t,y(t))，具体代码如下：function dydt = matrixODE(t,y)A = reshape(y,[n,n]);dydt = reshape(A*reshape(y,[n,n]),[n^2,1]);end其中n是矩阵的维数，reshape函数可以将向量转化为矩阵，将矩阵转化为向量。

在函数handle中，我们将y(t)转化为一个n×n矩阵，然后计算A*y(t)，最后将结果转化为一个n²维列向量。