第二讲 基于搜索问题的求解(2)
- 格式:ppt
- 大小:164.00 KB
- 文档页数:17

(完整版)《搜索算法》知识点总结1. 搜索算法的概念搜索算法是计算机科学中的一类算法,用于在一个数据集合中查找指定的数据项。
搜索算法的目标是通过最少的计算操作来找到目标数据项,以提高效率。
2. 常见的搜索算法2.1 线性搜索线性搜索是最简单的搜索算法之一,它从数据集合的第一个元素开始逐个比较,直到找到目标数据项或者遍历整个数据集合。
线性搜索的时间复杂度为O(n),其中n为数据集合的大小。
2.2 二分搜索二分搜索是一种高效的搜索算法,它适用于有序的数据集合。
它将数据集合分为两部分,并与目标数据项进行比较,然后根据比较结果确定继续搜索的方向。
通过每次排除一半的数据,二分搜索的时间复杂度为O(log n),其中n为数据集合的大小。
2.3 哈希搜索哈希搜索通过将数据项映射到哈希表中的特定索引位置来进行搜索。
通过哈希函数,可以快速找到目标数据项所在的位置。
哈希搜索的时间复杂度为O(1),但需要额外的存储空间来存储哈希表。
2.4 深度优先搜索深度优先搜索是一种递归的搜索算法,它从起始点开始一直沿着一个路径搜索,直到找到目标数据项或者无法继续搜索。
如果搜索失败,则回溯到上一个节点,并探索其他路径。
深度优先搜索在有向图和无向图中均适用。
2.5 广度优先搜索广度优先搜索是一种逐层扩展的搜索算法,它从起始点开始,先访问所有直接相邻的节点,然后再访问相邻节点的邻居节点。
通过队列数据结构,广度优先搜索可以按层次进行遍历,直到找到目标数据项。
广度优先搜索适用于无权图和加权图。
3. 搜索算法的应用场景搜索算法在各种领域和实际问题中广泛应用,包括但不限于以下几个方面:- 文本搜索:在大规模的文本数据集中查找关键字或短语。
- 图像搜索:根据图像特征找到相似的图像。
- 数据库查询:根据指定条件查询数据库中的记录。
- 路径规划:在地图上找到最短路径或最优路径。
- 推荐系统:根据用户的兴趣和偏好推荐相关的内容。
- 人工智能:在机器研究和深度研究中的搜索空间优化等。




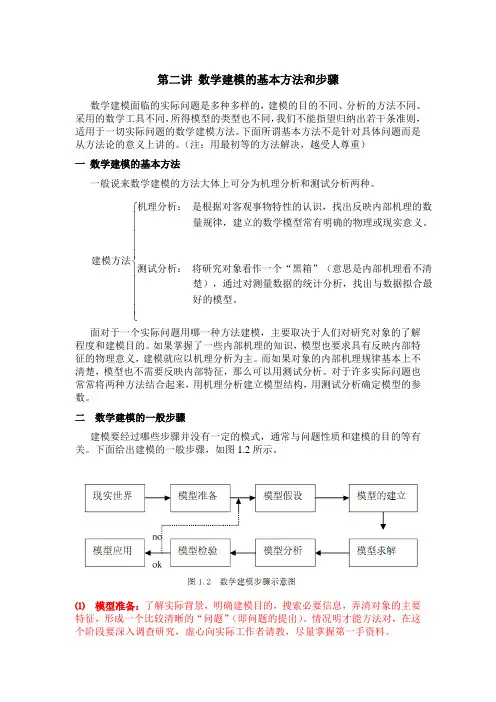
第二讲 数学建模的基本方法和步骤数学建模面临的实际问题是多种多样的,建模的目的不同、分析的方法不同、采用的数学工具不同,所得模型的类型也不同,我们不能指望归纳出若干条准则,适用于一切实际问题的数学建模方法。
下面所谓基本方法不是针对具体问题而是从方法论的意义上讲的。
(注:用最初等的方法解决,越受人尊重)一 数学建模的基本方法一般说来数学建模的方法大体上可分为机理分析和测试分析两种。
⎧⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎩机理分析: 是根据对客观事物特性的认识,找出反映内部机理的数 量规律,建立的数学模型常有明确的物理或现实意义。
建模方法测试分析: 将研究对象看作一个“黑箱”(意思是内部机理看不清 楚),通过对测量数据的统计分析,找出与数据拟合最 好的模型。
面对于一个实际问题用哪一种方法建模,主要取决于人们对研究对象的了解程度和建模目的。
如果掌握了一些内部机理的知识,模型也要求具有反映内部特征的物理意义,建模就应以机理分析为主。
而如果对象的内部机理规律基本上不清楚,模型也不需要反映内部特征,那么可以用测试分析。
对于许多实际问题也常常将两种方法结合起来,用机理分析建立模型结构,用测试分析确定模型的参数。
二 数学建模的一般步骤建模要经过哪些步骤并没有一定的模式,通常与问题性质和建模的目的等有关。
下面给出建模的一般步骤,如图1.2所示。
⑴ 模型准备:了解实际背景,明确建模目的,搜索必要信息,弄清对象的主要特征,形成一个比较清晰的“问题”(即问题的提出)。
情况明才能方法对,在这个阶段要深入调查研究,虚心向实际工作者请教,尽量掌握第一手资料。
⑵模型假设:根据对象的特征和建模目的,抓住问题的本质,忽略次要因素,作出必要的、合理的简化假设。
对于建模的成败这是非常重要和困难的一步。
假设不合理或太简单,会导致错误的或无用的模型;假设作得过分详细,试图把复杂对象的众多因素都考虑进去,会使你很难或无法继续下一步的工作。
常常需要在合理与简化之间作出恰当的折衷,要不段积累经验,并注意培养和充分发挥对事物的洞察力和判断力。





第1篇摘要:随着信息技术的飞速发展,搜索算法在各个领域都发挥着至关重要的作用。
本文以设计搜索算法为主题,通过教学实践,探讨了如何将搜索算法的理论知识与实际应用相结合,以提高学生的编程能力和解决问题的能力。
一、引言搜索算法是计算机科学中的重要分支,广泛应用于人工智能、数据挖掘、搜索引擎等领域。
在教学中,设计搜索算法的教学实践旨在培养学生的编程思维、算法设计能力和实际应用能力。
本文将结合教学实践,分析搜索算法的教学方法、实践案例和教学效果。
二、搜索算法的教学方法1. 理论讲解与案例分析相结合在教学过程中,首先讲解搜索算法的基本概念、原理和常用算法,如深度优先搜索、广度优先搜索、A搜索等。
接着,通过分析实际案例,让学生了解搜索算法在实际问题中的应用。
2. 实践操作与代码实现相结合为了让学生更好地理解搜索算法,可以让学生动手编写代码实现各种搜索算法。
通过实践操作,让学生亲身体验搜索算法的设计过程,提高编程能力。
3. 多种算法对比分析在教学中,可以引入多种搜索算法,如深度优先搜索、广度优先搜索、A搜索等,让学生对比分析它们的优缺点,从而更好地理解不同算法的特点和应用场景。
4. 优化与改进在学生掌握基本搜索算法的基础上,引导他们思考如何优化和改进算法。
例如,在广度优先搜索中,如何利用优先队列提高搜索效率;在A搜索中,如何设计启发式函数等。
三、实践案例1. 八数码问题八数码问题是一种经典的搜索问题,通过搜索算法找到将初始状态变为目标状态的最短路径。
在教学过程中,可以让学生使用深度优先搜索、广度优先搜索和A搜索解决八数码问题,并对比分析不同算法的搜索效率。
2. 图搜索问题图搜索问题广泛应用于路径规划、社交网络分析等领域。
在教学过程中,可以让学生使用广度优先搜索、深度优先搜索和A搜索解决图搜索问题,并分析不同算法在解决实际问题时的优缺点。
3. 字谜问题字谜问题是一种典型的组合优化问题。
在教学过程中,可以让学生使用回溯法解决字谜问题,通过编写代码实现搜索算法,提高学生的编程能力。