凸轮选型计算

偏心圆凸轮怎样计算偏心圆凸轮是一种常见的机械传动装置，它通过偏心圆的凸轮轴与连杆相连，实现机械运动的转换。

而要计算偏心圆凸轮的相关参数，需要考虑凸轮的形状、偏心圆的半径、连杆长度等因素。

下面将详细介绍偏心圆凸轮的计算方法。

我们需要确定凸轮的形状。

常见的凸轮形状有圆形、椭圆形、正弦形等。

不同形状的凸轮对应的运动规律不同，因此在计算前需要明确凸轮的形状。

我们需要确定偏心圆的半径。

偏心圆的半径决定了凸轮轴的偏心程度和凸轮的运动规律。

在计算时，需要根据具体的设计要求和运动特性确定偏心圆的半径。

接下来，我们需要确定连杆的长度。

连杆的长度决定了凸轮轴和工作机构之间的距离，直接影响到凸轮轴的运动和工作机构的运动。

在计算时，需要根据实际情况确定连杆的长度。

在确定了凸轮的形状、偏心圆的半径和连杆的长度后，我们可以开始计算凸轮的相关参数。

计算的关键是确定凸轮轴的旋转角度和工作机构的位置。

具体的计算方法如下：1. 根据凸轮的形状，可以确定凸轮轴的旋转角度与时间的关系。

对于圆形凸轮，凸轮轴的旋转角度与时间成正比；对于椭圆形凸轮，凸轮轴的旋转角度与时间的关系是非线性的；对于正弦形凸轮，凸轮轴的旋转角度与时间的关系是周期性的。

2. 根据凸轮轴的旋转角度，可以确定工作机构的位置与时间的关系。

工作机构的位置可以用连杆的长度和凸轮轴的旋转角度来计算。

3. 根据工作机构的位置与时间的关系，可以确定工作机构的运动规律。

根据具体的设计要求，可以计算工作机构的速度、加速度等参数。

在计算过程中，需要考虑摩擦、惯性等因素对凸轮轴和工作机构的影响。

这些因素会导致实际运动与理论计算有一定的偏差，因此在实际设计中需要进行修正和调整。

总结起来，偏心圆凸轮的计算涉及到凸轮的形状、偏心圆的半径、连杆的长度等因素。

通过确定凸轮轴的旋转角度和工作机构的位置，可以计算出相关的参数，进而确定凸轮的运动规律。

在实际设计中，还需要考虑摩擦、惯性等因素的影响，并进行修正和调整。

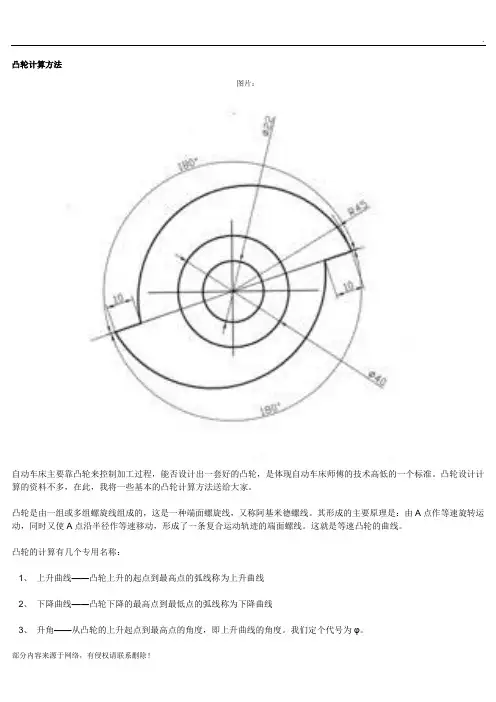
凸轮计算方法图片：自动车床主要靠凸轮来控制加工过程，能否设计出一套好的凸轮，是体现自动车床师傅的技术高低的一个标准。

凸轮设计计算的资料不多，在此，我将一些基本的凸轮计算方法送给大家。

凸轮是由一组或多组螺旋线组成的，这是一种端面螺旋线，又称阿基米德螺线。

其形成的主要原理是：由A点作等速旋转运动，同时又使A点沿半径作等速移动，形成了一条复合运动轨迹的端面螺线。

这就是等速凸轮的曲线。

凸轮的计算有几个专用名称：1、上升曲线——凸轮上升的起点到最高点的弧线称为上升曲线2、下降曲线——凸轮下降的最高点到最低点的弧线称为下降曲线3、升角——从凸轮的上升起点到最高点的角度，即上升曲线的角度。

我们定个代号为φ。

4、降角——从凸轮的最高点到最低点的角度，即下降曲线的角度。

代号为φ1。

5、升距——凸轮上升曲线的最大半径与最小半径之差。

我们给定代号为h，单位是毫米。

6、降距——凸轮下降曲线的最大半径与最小半径之差。

代号为h1。

7、导程——即凸轮的曲线导程，就是假定凸轮曲线的升角（或降角）为360°时凸轮的升距（或降距）。

代号为L，单位是毫米。

8、常数——是凸轮计算的一个常数，它是通过计算得来的。

代号为K。

凸轮的升角与降角是给定的数值，根据加工零件尺寸计算得来的。

凸轮的常数等于凸轮的升距除以凸轮的升角，即K=h/φ。

由此得h＝Kφ。

凸轮的导程等于360°乘以常数，即L＝360°K。

由此得L＝360°h/φ。

举个例子：一个凸轮曲线的升距为10毫米，升角为180°，求凸轮的曲线导程。

(见下图)解：L＝360°h/φ=360°×10÷180°＝20毫米升角(或降角)是360°的凸轮，其升距(或降距)即等于导程。

这只是一般的凸轮基本计算方法，比较简单，而自动车床上的凸轮，有些比较简单，有些则比较复杂。

在实际运用中，许多人只是靠经验来设计，用手工制作，不需要计算，而要用机床加工凸轮，特别是用数控机床加工凸轮，却是需要先计算出凸轮的导程，才能进行电脑程序设计. 走心机生产率的计算和凸轮设计公式的分析车削球面圆弧零件的凸轮设计计算。

自动车床主要靠凸轮来控制加工过程，能否设计出一套好的凸轮，是体现自动车床师傅的技术高低的一个标准。

凸轮设计计算的资料不多，在此，我将一些基本的凸轮计算方法送给大家。

凸轮是由一组或多组螺旋线组成的，这是一种端面螺旋线，又称阿基米德螺线。

其形成的主要原理是：由A点作等速旋转运动，同时又使A点沿半径作等速移动，形成了一条复合运动轨迹的端面螺线。

这就是等速凸轮的曲线。

凸轮的计算有几个专用名称：1、上升曲线——凸轮上升的起点到最高点的弧线称为上升曲线2、下降曲线——凸轮下降的最高点到最低点的弧线称为下降曲线3、升角——从凸轮的上升起点到最高点的角度，即上升曲线的角度。

我们定个代号为φ。

4、降角——从凸轮的最高点到最低点的角度，即下降曲线的角度。

代号为φ1。

5、升距——凸轮上升曲线的最大半径与最小半径之差。

我们给定代号为h，单位是毫米。

6、降距——凸轮下降曲线的最大半径与最小半径之差。

代号为h1。

7、导程——即凸轮的曲线导程，就是假定凸轮曲线的升角（或降角）为360°时凸轮的升距（或降距）。

代号为L，单位是毫米。

8、常数——是凸轮计算的一个常数，它是通过计算得来的。

代号为K。

凸轮的升角与降角是给定的数值，根据加工零件尺寸计算得来的。

凸轮的常数等于凸轮的升距除以凸轮的升角，即K=h/φ。

由此得h＝Kφ。

凸轮的导程等于360°乘以常数，即L＝360°K。

由此得L＝360°h/φ。

举个例子：一个凸轮曲线的升距为10毫米，升角为180°，求凸轮的曲线导程。

(见下图) 解：L＝360°h/φ=360°×10÷180°＝20毫米升角(或降角)是360°的凸轮，其升距(或降距)即等于导程。

这只是一般的凸轮基本计算方法，比较简单，而自动车床上的凸轮，有些比较简单，有些则比较复杂。

在实际运用中，许多人只是靠经验来设计，用手工制作，不需要计算，而要用机床加工凸轮，特别是用数控机床加工凸轮，却是需要先计算出凸轮的导程，才能进行电脑程序设计。

凸轮分割器凸轮分割器驱动角，又名动程角，是指输入轴驱动输出轴旋转1个工位，输入轴所旋转的角度。

静止角，是指输入轴转动而输出轴静止，输入轴所旋转的角度。

常用的驱动角有90度、120度、150度、180度、210度、240度、270度、300度、330度360度等。

二、驱动角+静止角=360度，因为输入轴旋转1圈，输出轴完成1次分割（1次分割=1次转位+1次停止）。

如上所描述，驱动角与静止角之比就是动静之比。

即决定了输出端面的转动与静止的时间比例。

因此，我们是可以根据转动时间与静止时间来选择驱动角的。

三、同时需要考虑到凸轮曲线的运动特性，驱动角越大，凸轮曲线越平缓，其运转越平稳。

因此应尽量选择驱动角度较大的凸轮分割器。

四、举例说明1：如转动时间是0.5秒，静止时间是0.5秒，应该选多大的驱动角呢，首先我们先来看动静比，即为0.5秒：0.5秒=1:1，也就是驱动角与静止角比例为1:1，因此我们推荐驱动角为180度；五、举例说明2：如转动时间为0.5秒，静止时间为1.5秒，又该怎么选呢，动静比为1:3，即驱动角与静止角之比为1:3，驱动角为90度，这个驱动角是否合适呢？从运动特性来看，其驱动角为90度下运转平稳性不好，不建议选用，最好选用驱动角为270度，静止时间需通过输入轴来延长所需要的静止时间。

因此，选择驱动角是要综合考虑动静比、驱动角曲线的运转特性等因素。

通过以上介绍，不知你是否可以选好凸轮分割器的驱动角呢。

==88888888888888888888888888888888888888888888888888888888凸轮分割器选型手册范例及计算使用场合：间歇回转圆盘选用适当大小及规格之间歇分割器及所需动力之马达，请依据下列之计算，参考图一所示的设计资料：解答如下：1-1 间歇分割定位等份：S=81-2 转位角度θ=360°×0.25/（0.25+0.5）=360°×1/3=120°1-3 入力轴之回转数：N=60/t1×θ/360=60/0.25×120/360=80rpm1-4 凸轮曲线是变形正弦曲线，因此Vm=1.76，Am=5.53，Qm=0.9871-5 负载安全系数fe=1.81-6 摩擦系数μ=0.2(1)惯性扭力：Ti（a）转盘重量：W1，夹具重量：W2,工件重量：W3，则：W1=л×20²×3×7.85×1/1000=29.59KgW2=4×8=32KgW3=0.5×8=4Kg（b）回转盘惯性矩：I1，夹具惯性矩：I2，工件惯性矩：I3，各为：I1=W1R1²/2G=29.59×0.2²/2×9.8=0.060kgf.m.s²I2=W2R2²/G=32×0.15²/9.8=0.0735kgf.m.s²I3=W3R3²/G=4×0.15²/9.8=0.00992kgf.m.s²（c）总惯性矩：II=I1+I2+I3=0.060+0.0735+0.0092=0.1427kgf.m.s²因为是单道程，m=ITi=226.2Am×I.N²/S(θ/m)²=226.2×5.53×0.1427×80²/8×120²=9.916kgf.m (2)摩擦扭矩：TfTf=μ.W.R=0.2×(29.59+32+4)×0.15=1.968kgf.m(3)工作扭矩：Tw在间歇分割时没有作功，因此Tw=0(4)以上总负载扭矩：TtTt=Ti+Tf+Tw=9.916+1.9968+0=11.884kgf.m实际负载扭矩：Te=Tt.fe=11.884×1.8=21.391kgf.m入力轴扭矩：Tc，注：入力轴起动负载扭矩视为0，因此Tca=0Tc=360/θ.S×Qm×Te=360/(120×8)×0.987×21.391=7.917kgf.m计算所需之马力，假设马达的效率为60%，则：P=Tc×N×9.8/9550×0.6=7.917×80×9.8/9550×0.6=1.083kw事实上，以上所计算之值为起动时之最大马力，而连续传动所需之马力：Pa=P×1/2=1.083×1/2=0.542kw(5)选择适用之间歇分割器根据以上所计算之资料以及入力轴之转数80rpm来选择，请参考说明书上所记载，凡是出力轴扭矩高于以上所计算之Te值者均可选用。

凸轮计算方法图片：自动车床主要靠凸轮来控制加工过程，能否设计出一套好的凸轮，是体现自动车床师傅的技术高低的一个标准。

凸轮设计计算的资料不多，在此，我将一些基本的凸轮计算方法送给大家。

凸轮是由一组或多组螺旋线组成的，这是一种端面螺旋线，又称阿基米德螺线。

其形成的主要原理是：由A点作等速旋转运动，同时又使A点沿半径作等速移动，形成了一条复合运动轨迹的端面螺线。

这就是等速凸轮的曲线。

凸轮的计算有几个专用名称：1、上升曲线——凸轮上升的起点到最高点的弧线称为上升曲线2、下降曲线——凸轮下降的最高点到最低点的弧线称为下降曲线3、升角——从凸轮的上升起点到最高点的角度，即上升曲线的角度。

我们定个代号为φ。

4、降角——从凸轮的最高点到最低点的角度，即下降曲线的角度。

代号为φ1。

5、升距——凸轮上升曲线的最大半径与最小半径之差。

我们给定代号为h，单位是毫米。

6、降距——凸轮下降曲线的最大半径与最小半径之差。

代号为h1。

7、导程——即凸轮的曲线导程，就是假定凸轮曲线的升角（或降角）为360°时凸轮的升距（或降距）。

代号为L，单位是毫米。

8、常数——是凸轮计算的一个常数，它是通过计算得来的。

代号为K。

凸轮的升角与降角是给定的数值，根据加工零件尺寸计算得来的。

凸轮的常数等于凸轮的升距除以凸轮的升角，即K=h/φ。

由此得h＝Kφ。

凸轮的导程等于360°乘以常数，即L＝360°K。

由此得L＝360°h/φ。

举个例子：一个凸轮曲线的升距为10毫米，升角为180°，求凸轮的曲线导程。

(见下图)解：L＝360°h/φ=360°×10÷180°＝20毫米升角(或降角)是360°的凸轮，其升距(或降距)即等于导程。

这只是一般的凸轮基本计算方法，比较简单，而自动车床上的凸轮，有些比较简单，有些则比较复杂。

在实际运用中，许多人只是靠经验来设计，用手工制作，不需要计算，而要用机床加工凸轮，特别是用数控机床加工凸轮，却是需要先计算出凸轮的导程，才能进行电脑程序设计. 走心机生产率的计算和凸轮设计公式的分析车削球面圆弧零件的凸轮设计计算CM1107机床调整卡及凸轮设计CM1107机床调整卡及凸轮设计自动车床在投入生产之前，必须做好以下几项生产准备工作：1．拟订零件的加工工艺过程，选用适当的切削用量标准刀具和辅具，必要时设计特殊的刀辅具；2．根据零件的加工工艺，拟订机床调整卡；3．根据调整卡的数据，设计并制造凸轮；4．按照调整卡调整机床下面以零件“轮轴”的加工为例（见表2-2）说明拟订工艺过程的注意事项，调整卡的制定方法和凸轮曲线的绘制方法。

凸轮分割器选型相关搜索:凸轮, 选型例一回转圆盘式凸轮分割器选型：选用适当大小及规格之间歇分割器及所需动力之马达，请依据下列方法计算，参考图一所示〈参考图一〉回转圆盘式凸轮分割器设计资料【1】间歇分割定位等分∶N=6【2】每等分回转时间∶秒【3】输入轴回转数∶n=80rpm∶凸轮轴速度(每分钟回转数)【4】凸轮曲线∶修正正弦曲线【5】回转盘尺寸∶￠300*20【6】夹具重量∶3kg／组【7】工件重量∶0.25kg／组【8】转盘依靠其底部滑动面支持本身重量负荷，有效半径∶R=100㎜【9】夹具固定节圆直径￠200㎜处解答1~1间歇分割定位等分∶N=61~2回转时间和定位时间之比为1:2，因此转位角度，h=360°*1/（1+2）=120°1~3输入轴回转数∶n=80rpm1~4凸轮曲线：修正正弦曲线，因此Vm=1.76, Am=5.53, Qm=0.991~5负载扭矩∶Tt惯性扭矩∶Tt(a)转盘重量∶W1；夹具重量∶W2 ；工作重量∶W3 则W1= 3.1415926*(30/2)²*2*7.8*1/1000=11.026(kg)W2=3*6=18(kg)W3=0.25*6=1.5(kg)(b)回转盘惯性矩∶I1; 夹具惯性矩∶I2 ;工作惯性矩∶I3 各为I1=W1*R²/2G=11.026*0.15²/(2x9.8)=0.0126(kg.cm.s²)I2=W2*Re²/G=18*0.1²/9.8=0.018(kg.cm.s²)I3=W3*Re²/G=1.5x0.1²/9.8=0.0015(kg.cm.s²)(c)总惯性矩∶II=I1+I2+I3 I=0.0126+0.018+0.0015=0.032(kg.cm.s²)(d)输出轴最大角加速度∶ε=(Am*2*3.1415926/N)*((360/ h)*(n/60))²ε=(5.53*2*3.1415926/6)*((360/120)*(80/60))²=92.66(rad/s²)(e)静扭矩(惯性扭矩)∶TiTi=I*Ti=0.032*92.66=2.965(kg.cm)摩擦扭矩∶TfW=W1+W2+W3Tf=u*W*Re=0.15*(11.026+18+1.5)*0.1=0.458(kg.cm)摩擦系数：u=0.15(f)工作扭矩Tw在间歇分割时没有作功因此Tw=0以上总负载扭矩∶TtTt=Ti+Tf+Tw=2.965+0.458+0=3.423(kg.m)1~6实际负载扭矩∶Te 安全负载之因数 fc=1.5Te=Tt*fc=3.423*1.5= 5.135(kg.m)1~7输入轴扭矩∶Tc 注∶输入轴起动负载扭矩视为0，因此Tca=0Tc=360/ h*N *Qm*Te + Tca= 360/120*6*0.99*5.135 =2.54(kg.m)1~8计算所需之马力∶PP=Tc*n/(716*Q)(HP) 或 P= Tc*n/(975*Q)(kw)假设效率Q=60%那么P=2.54x80/716x0.6=0.47(HP) 或P=2.54x80/975x0.6=0.34(kw)事实上，以上所计算数值为起动时最大马力，而连续传动所需之马力为1/21~9选择适用之间歇分割器根据以上所计算之资料以及输入轴转速80rpm来选择，请参考说明书上所记载，凡是输出轴扭矩高于以上所计算之Te值者均可选用。

03凸轮机构的设计计算凸轮机构是一种用于驱动轴、执行轴、连杆和滑块等机械元件的传动装置，广泛应用于各种机械设备和工业领域中。

它的设计计算涉及到凸轮的形状、尺寸和运动规律等方面，下面将详细介绍凸轮机构的设计计算。

第一步：确定凸轮的类型和运动规律凸轮的类型有很多种，包括圆柱形凸轮、球形凸轮、心形凸轮等。

不同类型的凸轮适用于不同的机械运动规律。

在确定凸轮类型之后，需要确定凸轮的运动规律，例如旋转、摆动、直线运动等。

根据需要确定凸轮的运动规律可以为后续计算提供基础。

第二步：计算凸轮的基本参数计算凸轮的基本参数包括凸轮的直径、偏距、厚度等。

凸轮的直径决定了凸轮的外形尺寸；凸轮的偏距决定了凸轮所产生的运动；凸轮的厚度决定了凸轮的刚度和强度。

第三步：绘制凸轮的曲线在计算凸轮的曲线时，可以采用手工绘制或计算机辅助设计（CAD）绘制。

在绘制凸轮的曲线时，需要根据凸轮的运动规律和基本参数，按照一定比例绘制凸轮的曲线。

第四步：计算凸轮机构的运动参数凸轮机构的运动参数包括凸轮的角速度、轴向加速度、径向加速度、凸轮与随动件之间的相对速度等。

这些参数可以通过对凸轮轮廓曲线进行微分和积分计算得到。

第五步：计算凸轮机构的受力和刚度凸轮机构的受力和刚度是设计计算的重要内容。

在计算凸轮机构的受力和刚度时，需要考虑凸轮与随动件之间的力、力矩和弯曲等因素，并根据材料的强度和刚度计算凸轮的设计要求。

第六步：优化凸轮机构的设计在完成凸轮机构的设计计算后，可以进行适当的优化设计。

优化设计可以根据实际需要调整凸轮的形状、尺寸和运动规律等，以实现更好的运动效果和工作性能。

总结起来，凸轮机构的设计计算包括确定凸轮的类型和运动规律、计算凸轮的基本参数、绘制凸轮的曲线、计算凸轮机构的运动参数、计算凸轮机构的受力和刚度，以及优化凸轮机构的设计等多个步骤。

这些计算需要依靠数学和力学等相关知识，并结合实际工作需求进行。

设计人员应根据实际情况和要求进行适当调整和改进，以满足不同工程和应用领域的需求。

目录一：产品介绍与外型选购1.弧面凸轮分割器（1）介绍（2）型式选定参数（3）外形图及尺寸（4）技术参数表2.平行凸轮分割器（1）介绍（2）型式选定参数（3）外形图及尺寸（4）技术参数表3.圆柱凸轮分割器（1）介绍（2）示意外形图4.凸轮及模具制作二：选型范例三：新品推荐。

凸轮间歇机构广泛应用在制药机械、印刷机械、包装机械、玻璃机械、陶瓷机械、烟草机械、机床加工中心、自动送料机等需要把连续运转转化为步进动作的各种自动化机械上。

该产品具有步进定位精度高、高速运转平稳、传递扭矩大、定位时自锁等显著优点，是替代槽轮机构、不完全齿轮机构、棘轮机构等传统间歇机构的最理想产品。

“一：产品介绍与外型选择1、弧面凸轮分割器“弧面凸轮分割器”是输入轴上的空间立体凸轮与输出从动轴上的从动滚子无间隙啮合形成的机构。

其特点是：凸轮基面为圆弧回转体，从动滚子轴线与输出轴垂直，并与凸轮轴线处在同一平面内。

凸轮廓面的曲线段驱使分割盘转位，直线段使分割盘静止并自锁。

通过该机构将连续的输入回转运动转化为间歇的步进输出运动。

该种类型的分割器由于精度高、速度快、扭矩大、体积小等显著特点，广泛应用于各种需要步进驱动的自动组合机，加工机械，金属加工器械，输送机步进驱动，包装机，食品机械，分装设备，医药器械，自动检测机，挤压入料装置，以及在其他工业使用的间歇分割机。

弧面凸轮分割器按照输出轴的输出类型分为：轴式、法兰式、平台桌面式.型式选定需提供如下参数：1．中心距(即输入轴与输出轴间的距离)：45、50、63、70、80、83、100、110、125、140、150、160、175、180、200、250、3502．分割数：2、3、4、5、6、8、9、10、12、16、24、32、……3．动程角：90°；120°；180°；240°；270°；300°等4．凸轮旋向：右旋R为标准型、左旋L（见下图）5．曲线类型：（1）MS曲线（优选变正弦曲线，标准）、（2）MT 曲线、（3）MCV曲线、（4）按用户要求曲线。

凸轮曲线系修正正弦曲线，因此负载扭矩计算Tt1.惯性扭矩：Tt(a)转盘重量：W 1 夹具重量：W 2 工作重量：W 3 则W1=99.879318W2=56W3=0(b)回转盘惯性矩：I 1 夹具惯性矩：I 2 工件惯性矩：I 3 各为I 1=W 1R 2/2GI1= 1.03191642I 2=W 1Re 2/GI2=0.05714286I 3=W 1Re 2/GI3=0(c)总惯性矩：II=I 1+I 2+I 3I= 1.08905928(d)出力轴最大角加速度：Am×2/N×(360/h×n/60)239.089358(e)静扭矩(惯性扭矩)：Ti 以下为自动计算分割器选型计Ti=Ti=42.57062812. 摩擦扭矩：TfTf=Tf= 2.338189773. 作功扭矩：Tw在间歇分割时没有作功，因此Tw=0Tw=04.以上总负载扭矩：TtTt=Ti+Tf+Tw Tt=44.9088179实际负载扭矩：Te 安全负载之因数fc fc= 1.5Te=Tt x fc Te=67.3632268入力轴扭矩：Tc 注：入力轴起动负载扭矩视为0，因此Tca=0Tca=0Tc=360/（h×N） × Qm × te + Tca Tc=25.0085979计算所需之马力：PP=Tc×n/716×n(HP) 或 P= Tc×n/975×n(kw) Thp=Tc×n/716×n(HP) 或 P=Tc×n/975×n 假设效率n=60%那么P= 3.49282094P= 2.5649844事实上，以上所计算之值为起动时之最大马力，而连续传动所需之马力为1/2选择适用之间歇分割器(INDEXING DRIVES)根据以上所计算之资料以及入力轴之转数n rpm来选择，请参考说明书上所记载，凡是出力Vm:最大非向性速度Am:最大非向性之加速度Qm:凸轮轴最大扭力系数:角加速度h:入力轴转位(驱动)角度N: 分割数秒转位时间(仅回转时间）rpm凸轮轴速度(每分钟回转数) 修正正弦曲线cm单位为cm cm单位为cm g/cm3单位为g/cm3kg／组kg／组m100mm处m支撑处直径200mm °秒常数：pi=3.1416G=9.8Am=5.53Qm=0.99kgkgkg(kg x m x s2)rad/s2kg x m x s2kg x m x s2kg x m x s2选型计算公式如下参数取夹具重心到转盘轴心距离的2倍回转时间和定位时间之比选为1:2，因此转位角度h=360°x1/1+2=120°包括回转时间和停止时间kg· mkg· mkg· m一般取1.5~2对照分割器参数表选取＞Te值的型号kg x mkg x mP=Tc×n/975×nHPkw是出力轴扭矩高于以上所计算之Te值者均可选用。

凸轮曲线方程公式
凸轮曲线的一般方程为：
\(x = f(t)\)
\(y = g(t)\)
其中，\(f(t)\)和\(g(t)\)分别是关于参数\(t\)的函数。

具体的凸轮曲线方程取决于具体的凸轮形状和设计要求。

常见的一些凸轮曲线方程公式有：
1. 圆形凸轮：
\(x = R \cdot \cos(t)\)
\(y = R \cdot \sin(t)\)
其中，\(R\)为凸轮的半径。

2. 奥伊拉曲线（一种常用的凸轮曲线）：
\(x = R \cdot e^{a \cdot t} \cdot \cos(t)\)
\(y = R \cdot e^{a \cdot t} \cdot \sin(t)\)
其中，\(R\)为凸轮的半径，\(a\)为曲线的形状参数。

3. 椭圆形凸轮：
\(x = R \cdot \cos(t)\)
\(y = R \cdot \sin(t) \cdot \frac{b}{a}\)
其中，\(R\)为凸轮的半径，\(a\)和\(b\)为轴向长度的一半。

这些方程仅为常见的凸轮曲线方程，实际上可以根据具体的设计要求和凸轮形状进行调整和推导。