matlab例题

习题：1， 计算⎥⎦⎤⎢⎣⎡=572396a 与⎥⎦⎤⎢⎣⎡=864142b 的数组乘积。

2， 对于B AX =，如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=282637B ，求解X 。

3， 已知：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321a ，分别计算a 的数组平方和矩阵平方，并观察其结果。

4， 角度[]604530=x ，求x 的正弦、余弦、正切和余切。

(应用sin,cos,tan.cot)5， 将矩阵⎥⎦⎤⎢⎣⎡=7524a 、⎥⎦⎤⎢⎣⎡=3817b 和⎥⎦⎤⎢⎣⎡=2695c 组合成两个新矩阵： （1）组合成一个4⨯3的矩阵，第一列为按列顺序排列的a 矩阵元素，第二列为按列顺序排列的b 矩阵元素，第三列为按列顺序排列的c 矩阵元素，即 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡237912685574（2）按照a 、b 、c 的列顺序组合成一个行矢量，即 []2965318772546， 将(x -6)(x -3)(x -8)展开为系数多项式的形式。

(应用poly,polyvalm)7， 求解多项式x 3-7x 2+2x +40的根。

(应用roots)8， 求解在x =8时多项式(x -1)(x -2) (x -3)(x -4)的值。

(应用poly,polyvalm)9， 计算多项式9514124234++--x x x x 的微分和积分。

(应用polyder,polyint ，poly2sym)10， 解方程组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡66136221143092x 。

(应用x=a\b)11， 求欠定方程组⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡5865394742x 的最小范数解。

(应用pinv) 12， 矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=943457624a ，计算a 的行列式和逆矩阵。

(应用det,inv)13， y =sin(x )，x 从0到2π，∆x =0.02π，求y 的最大值、最小值、均值和标准差。

matlab程序设计例题及答案1.编写程序：计算1/3+2/5+3/7+……+10/21法一： s=0;for i=1:10s=s+i/(2*i+1); end ss =法二：sum((1:10)./(3:2:21)) ans =2.编写程序：计算1~100中即能被3整除，又能被7整除的所有数之和。

s=0;for i=1:100if mod(i,3)==0&&mod(i,7)==0 s=s+i; end,end ss =2103.画出y=n！的图,阶乘的函数自己编写，禁用MATLAB 自带的阶乘函数。

x=1:10; for i=1:10try y(i)=y(i-1)*i; catch y(i)=1; end,end plot(x,y)106123456789104.一个数恰好等于它的因子之和，这个数就称为完数。

例如，6的因子为1，2,3，而6=1+2+3，因此6就是一个完数。

编程找出20XX以内的所有完数。

g=;for n=2:20XX s=0;for r=1:n-1if mod(n,r)==0 s=s+r; end endif s==ng=[g n]; end end gg =6 28 4965.编写一个函数，模拟numel函数的功能，函数中调用size函数。

function y=numelnumel(x) m=size(x); y=m(1)*m(2);numelnumel([1 2 3;4 5 6])ans =66. 编写一个函数，模拟length函数的功能，函数中调用size函数。

function y=lengthlength(x) m=size(x);y=max(m(1),m(2));lengthlength([1 2 3;4 5 6])ans =37.求矩阵rand的所有元素和及各行平均值，各列平均值。

s=rand(5);sum=sum(sum(s)) mean2=mean(s,2) mean1=mean(s)sum =mean2 =mean1 =8.编程判断1001,1003,1007，1009，1011为素数，若不是，输出其约数。

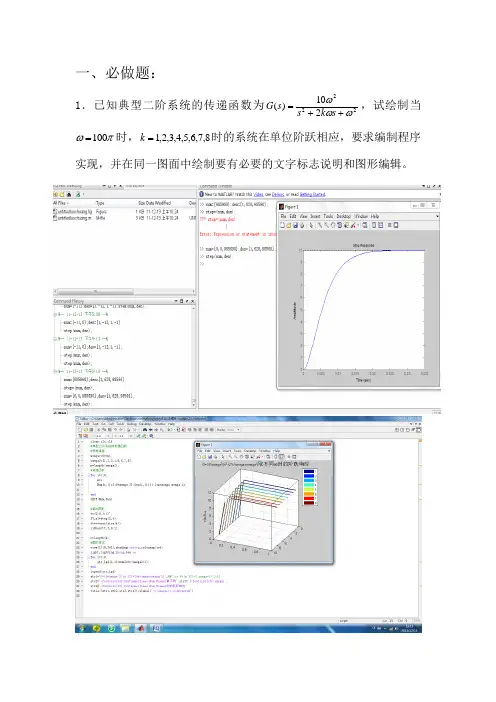
一、必做题：
1．已知典型二阶系统的传递函数为2
22210)(ωωω++=s k s s G ，试绘制当100ωπ=时，8,7,6,5,4,3,2,1=k 时的系统在单位阶跃相应，要求编制程序实现，并在同一图面中绘制要有必要的文字标志说明和图形编辑。

2．试用Simulink构建三相整流逆变电路。

要求：给出整流桥桥臂电流和电压，整流桥输出电压和逆变桥输入电压，逆变滤波以后的输出电压，并有必要的分析和说明。

第二题 、选做题
5、已知某控制系统的开环传递函数，)
9)(5()2()()(2+++=s s s s k s H s G ，要求绘制系统正反馈、负反馈时系统的根轨迹，并判断系统的稳定性有何区别。

要求编制相应的程序实现。

7、已知如图1所示的电路中，电源
电压10)(=t u s V 时，L =2H ，Ω=1R 求解
图中的电流波形。

假设初始电流
A i 2)0(=，试用Simulink 工具箱搭建模型求出电流波形。

15．用Simulink构建如图8所示的电路，其中R1＝5 Ώ，R2＝3 Ώ，R3＝4 Ώ，R4＝2 Ώ，R5＝1 Ώ，求电流I。

习题：1， 计算⎥⎦⎤⎢⎣⎡=572396a 与⎥⎦⎤⎢⎣⎡=864142b 的数组乘积。

2， 对于B AX =，如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=282637B ，求解X 。

3， 已知：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321a ，分别计算a 的数组平方和矩阵平方，并观察其结果。

4， 角度[]604530=x ，求x 的正弦、余弦、正切和余切。

(应用sin,cos,tan.cot)5， 将矩阵⎥⎦⎤⎢⎣⎡=7524a 、⎥⎦⎤⎢⎣⎡=3817b 和⎥⎦⎤⎢⎣⎡=2695c 组合成两个新矩阵： （1）组合成一个4⨯3的矩阵，第一列为按列顺序排列的a 矩阵元素，第二列为按列顺序排列的b 矩阵元素，第三列为按列顺序排列的c 矩阵元素，即 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡237912685574（2）按照a 、b 、c 的列顺序组合成一个行矢量，即 []2965318772546， 将(x -6)(x -3)(x -8)展开为系数多项式的形式。

(应用poly,polyvalm)7， 求解多项式x 3-7x 2+2x +40的根。

(应用roots)8， 求解在x =8时多项式(x -1)(x -2) (x -3)(x -4)的值。

(应用poly,polyvalm)9， 计算多项式9514124234++--x x x x 的微分和积分。

(应用polyder,polyint ，poly2sym)10， 解方程组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡66136221143092x 。

(应用x=a\b)11， 求欠定方程组⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡5865394742x 的最小范数解。

(应用pinv)12， 矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=943457624a ，计算a 的行列式和逆矩阵。

(应用det,inv)13， y =sin(x )，x 从0到2π，∆x =0.02π，求y 的最大值、最小值、均值和标准差。

Matlab例题汇总：【例2-4】两个矩阵分别为[1 2 3;4 5 6;7 8 9]和[1 1 1;2 2 2;3 3 3]，求两者相加的和。

a=[1 2 3;4 5 6;7 8 9];b=[1 1 1;2 2 2;3 3 3];c=a+b【例2-5】两个矩阵分别为[1 2 3;4 5 6;7 8 9]和[1 1 1]，阶数不同，求两者相减的差。

a=[1 2 3;4 5 6;7 8 9];b=[1 1 1];c=a-b【例2-6】两个矩阵相乘，矩阵a为，矩阵b为，分别计算c=a*b和d=b*a。

a=[1 2 3;4 5 6;7 8 9];b=[1 2 3];c=a*b% 将第三句c=a*b改成d=b*a，再运行一次% 【例2-7】两个数组相乘，数组a为，数组b为，求两数组的乘法。

% 在命令窗口输入两数组，计算c=a.*b：a=[1 2 3];b=[4 5 6];c=a.*b% 【例2-8】两个矩阵相除，矩阵a和b均为3×3阶矩阵。

a=rand(3)b=rand(3)c=a/bd=b\a% 【例2-9】数组a为，数组b为，求两数组的除法。

a=[1 2 3];b=[4 5 6];c=a.\bc=b./a% 【例2-10】矩阵a为[1 2;3 4]，求它的1.5次幂。

a=[1 2;3 4];c=a^1.5% 【例2-11】数组a为[1 2 3]，数组b为[4 5 6]，求数组的幂c=a.^b。

a=[1 2 3];b=[4 5 6];c=a.^b% 【例2-12】数组a为[1 2 3]，求数组的幂c=a.^2。

a=[1 2 3];c=a.^2% 【例2-13】数组a为[1 2 3]，求数组的幂运算c=2.^a。

a=[1 2 3];c=2.^a% 【例2-14】矩阵a为[1 2 3;4 5 6;7 8 9]，计算a的转置。

a=[1 2 3;4 5 6;7 8 9];c=a'% 【例2-15】矩阵a为[1+2i 3+4i]，计算a的转置。

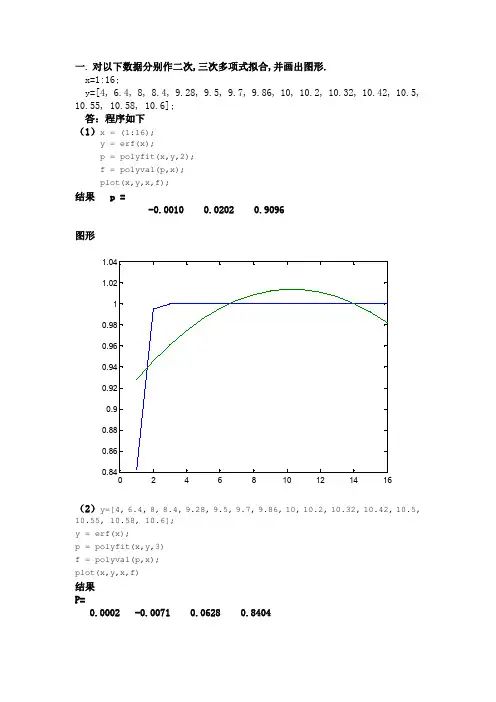
一.对以下数据分别作二次,三次多项式拟合,并画出图形.x=1:16;y=[4,6.4,8,8.4,9.28,9.5,9.7,9.86,10,10.2,10.32,10.42,10.5, 10.55,10.58,10.6];答：程序如下（1）x=(1:16);y=erf(x);p=polyfit(x,y,2);f=polyval(p,x);plot(x,y,x,f);结果p=-0.00100.02020.9096（2）y=[4,6.4,8,8.4,9.28,9.5,9.7,9.86,10,10.2,10.32,10.42,10.5, 10.55,10.58,10.6];y=erf(x);p=polyfit(x,y,3)f=polyval(p,x);plot(x,y,x,f)结果P=0.0002-0.00710.06280.8404二.在[0,4pi]画sin(x),cos(x)(在同一个图象中);其中cos(x)图象用红色小圆圈画.并在函数图上标注“y=sin(x)”,“y=cos(x)”,x轴,y轴,标题为“正弦余弦函数图象”.答：程序如下x=[0:720]*pi/180;plot(x,sin(x),x,cos(x),'ro');x=[2.5;7];y=[0;0];s=['y=sin(x)';'y=cos(x)'];text(x,y,s);xlabel('正弦余弦函数图象'),ylabel('正弦余弦函数图象')图形如下三.选择一个单自由度线性振动系统模型，自定质量、弹簧刚度、阻尼、激振力等一组参数，分别编程（m 文件）计算自由和强迫振动时的响应，并画出振动曲线图。

（要求画出该单自由度线性振动系统模型图）其中质量为m=1000kg,弹性刚度k=48020N/m,阻尼c=1960N.s/m,激振力f(t)=0.阻尼比ζ的程序p=1960/(2*sqrt(48020*1000))求得p=0.1414而p为阻尼比ζ强迫振动时的响应程序g =tf([-101],[48020048020*1.9848020]);bode(g)图形g =tf([001],[0001]);bode(g)振动曲线图程序：函数文件function dx =rigid(t,x)dx =zeros(2,1);dx(1)=x(2);dx(2)=(-48020*x(1)-1960*x(2))/1000;命令文件options =odeset('RelTol',1e-4,'AbsTol',[1e-41e-4]);[T,X]=ode45(@rigid,[012],[11],options);plot(T,X(:,1),'-')其图形如下024681012-6-5-4-3-2-11234单自由度线性强迫振动系统模型图其中质量为m=1000kg,弹性刚度k=48020N/m,阻尼c=1960N.s/m，f(t)=cos(3*pi*t)振动曲线图程序：函数文件function dx=rigid(t,x)dx=zeros(2,1);dx(1)=x(2);dx(2)=(-48020*x(1)-1960*x(2))/1000+cos(3*pi*t);命令文件options=odeset('RelTol',1e-4,'AbsTol',[1e-41e-4]);[T,X]=ode45(@rigid,[020],[11],options);plot(T,X(:,1),'-')力等一组参数，建立Simulink仿真模型框图进行仿真分析。

1
3.2 程序控制结构 3.2.1 顺序结构 1．数据的输入 从键盘输入数据，则可以使用input函数来进
行，该函数的调用格式为： A=input(提示信息，选项)； 其中提示信息为一个字符串，用于提示用户 输入什么样的数据。 如果在input函数调用时采用's'选项，则允 许用户输入一个字符串。例如，想输入一 个人的姓名，可采用命令： xm=input('What''s your name?','s');
%输出商品实际销售价格
3．try语句 语句格式为：
try 语句组1
catch 语句组2
end try语句先试探性执行语句组1，如果语句组1
在执行过程中出现错误，则将错误信息赋 给保留的lasterr变量，并转去执行语句组2。
1
例3-7 矩阵乘法运算要求两矩阵的维数相容，否则 会出错。先求两矩阵的乘积，若出错，则自动转 去求两矩阵的点乘。
语句组m
else 语句组n
end 语句用于实现多分支选择结构。
1
例3-5 输入一个字符，若为大写字母，则输出其 对应的小写字母；若为小写字母，则输出其对应 的大写字母；若为数字字符则输出其对应的数值， 若为其他字符则原样输出。 c=input('请输入一个字符','s'); if c>='A' & c<='Z' disp(setstr(abs(c)+abs('a')-abs('A'))); elseif c>='a'& c<='z' disp(setstr(abs(c)- abs('a')+abs('A'))); elseif c>='0'& c<='9' disp(abs(c)-abs('0')); else disp(c); end

以下各题均要求编程实现，并将程序贴在题目下方。

1．从键盘输入任意个正整数，以0结束，输出那些正整数中的素数。

clc;clear;zzs(1)=input('请输入正整数：');k=1;n=0;%素数个数while zzs(k)~=0flag=0;%是否是素数，是则为1for yz=2:sqrt(zzs(k))%因子从2至此数平方根if mod(zzs(k),yz)==0flag=1;break;%非素数跳出循环endendif flag==0&zzs(k)>1%忽略0和1的素数n=n+1;sus(n)=zzs(k);endk=k+1;zzs(k)=input('请输入正整数：');enddisp(['你共输入了' num2str(k-1) '个正整数。

它们是：'])disp(zzs(1:k-1))%不显示最后一个数0if n==0disp('这些数中没有素数！')%无素数时显示elsedisp('其中的素数是：')disp(sus)end2．若某数等于其所有因子（不含这个数本身）的和，则称其为完全数。

编程求10000以内所有的完全数。

clc;clear;wq=[];%完全数赋空数组for ii=2:10000yz=[];%ii 的因子赋空数组for jj=2:ii/2 %从2到ii/2考察是否为ii 的因子if mod(ii,jj)==0yz=[yz jj];%因子数组扩展，加上jjendendif ii==sum(yz)+1wq=[wq ii];%完全数数组扩展，加上iiendenddisp(['10000以内的完全数为：' num2str(wq)])%输出3．下列这组数据是美国1900—2000年人口的近似值（单位：百万）。

（1） 若.2c bt at y t y ++=的经验公式为与试编写程序计算出上式中的a 、b 、c;（2） 若.bt ae y t y =的经验公式为与试编写程序计算出上式中的a 、b;（3） 在一个坐标系下，画出数表中的散点图（红色五角星），c bx ax y ++=2中拟合曲线图(蓝色实心线),以及.bt ae y = (黑色点划线)。

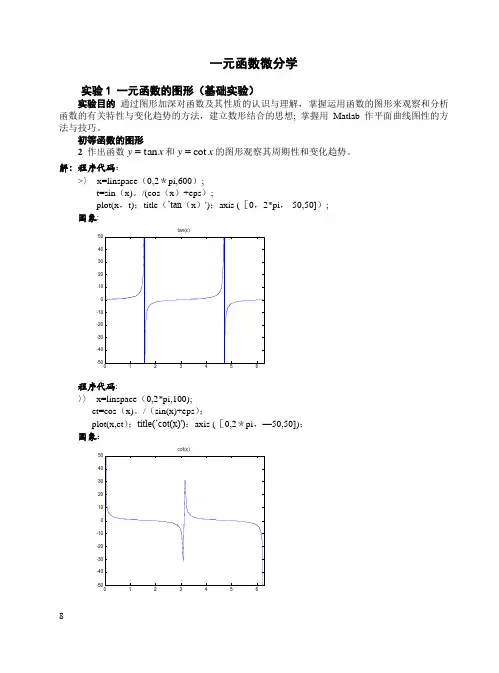
一元函数微分学实验1 一元函数的图形（基础实验）实验目的 通过图形加深对函数及其性质的认识与理解， 掌握运用函数的图形来观察和分析 函数的有关特性与变化趋势的方法，建立数形结合的思想; 掌握用Matlab 作平面曲线图性的方法与技巧。

初等函数的图形2 作出函数x y tan =和x y cot =的图形观察其周期性和变化趋势。

解：程序代码：>〉 x=linspace （0,2＊pi,600）; t=sin （x)。

/(cos （x ）+eps ）;plot(x ，t)；title （’tan （x ）')；axis (［0，2*pi ，-50,50]）; 图象:程序代码: 〉〉 x=linspace （0,2*pi,100); ct=cos （x)。

/（sin(x)+eps ）； plot(x,ct ）；title(’cot(x)')；axis (［0,2＊pi ，—50,50])； 图象：cot(x)4在区间]1,1[-画出函数xy 1sin =的图形。

解：程序代码:>> x=linspace （-1，1，10000）;y=sin(1。

/x ）; plot （x,y ）; axis （［-1，1，—2,2］） 图象：二维参数方程作图6画出参数方程⎩⎨⎧==t t t y tt t x 3cos sin )(5cos cos )(的图形：解：程序代码:>〉 t=linspace(0,2＊pi,100)； plot(cos(t ）.＊cos （5＊t ），sin(t ）。

*cos(3*t)); 图象：极坐标方程作图8 作出极坐标方程为10/t e r =的对数螺线的图形. 解：程序代码：〉〉 t=0:0.01:2*pi ； r=exp （t/10);polar(log(t+eps ）,log （r+eps)); 图象：90270分段函数作图10 作出符号函数x y sgn =的图形。

Zhangbin 87.5
Liping 90.0
Wangwei 78.0
Wujian 92.5
… …
6. 已知某班的5名学生的三门课成绩列表如下：
学生序号 1 2 3 4 5
高等数学 78 89 64 73 68
13
21
34
55
89
144
233
377
610
987
1597
2584
4181
6765
%【4】
a=input('input a:')
b=input('input b:')
c=input('input c:')
s=(a+b+c)/2;
Area=sqrt(s*(s-a)*(s-b)*(s-c))
运行结果：
input a:3
else y==x
disp('You won')
return
end
end
运行结果：
x = 22
Input number:20
y = 20
Low
Input number:30
y = 30
High
Input number:25
a = 3
input b:4
b = 4
input c:5
c = 5
Area = 6
%【7】
x=[ 1 3 5 7 9 ]
xx=rot90(rot90(x))
运行结果：
x =
1 3 5 7 9

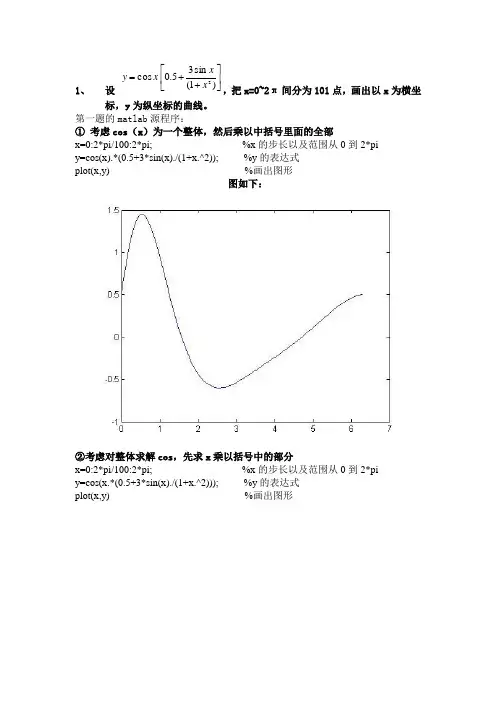
1、设⎥⎦⎤⎢⎣⎡++=)1(sin35.0cos2xxxy，把x=0~2π间分为101点，画出以x为横坐标，y为纵坐标的曲线。

第一题的matlab源程序：①考虑cos（x）为一个整体，然后乘以中括号里面的全部x=0:2*pi/100:2*pi; %x的步长以及范围从0到2*pi y=cos(x).*(0.5+3*sin(x)./(1+x.^2)); %y的表达式plot(x,y)%画出图形图如下：②考虑对整体求解cos，先求x乘以括号中的部分x=0:2*pi/100:2*pi; %x的步长以及范围从0到2*pi y=cos(x.*(0.5+3*sin(x)./(1+x.^2))); %y的表达式plot(x,y) %画出图形图如下：2、产生8×6阶的正态分布随机数矩阵R1, 求其各列的平均值和均方差。

并求该矩阵全体数的平均值和均方差。

第二题的matlab源程序如下：R1=randn(8,6) %产生正态分布随机矩阵R1 =1.0933 -0.7697 1.5442 -0.1924 1.4193 0.21571.1093 0.3714 0.0859 0.8886 0.2916 -1.1658-0.8637 -0.2256 -1.4916 -0.7648 0.1978 -1.14800.0774 1.1174 -0.7423 -1.4023 1.5877 0.1049-1.2141 -1.0891 -1.0616 -1.4224 -0.8045 0.7223-1.1135 0.0326 2.3505 0.4882 0.6966 2.5855-0.0068 0.5525 -0.6156 -0.1774 0.8351 -0.66691.5326 1.1006 0.7481 -0.1961 -0.2437 0.1873aver=(sum(R1(1:end,1:end)))./8 %产生各行的平均值aver =0.0768 0.1363 0.1022 -0.3473 0.4975 0.1044a=std(R1(1:end,1:end)) %产生各行的均方差也就是标准差a =1.0819 0.8093 1.3456 0.8233 0.8079 1.2150aver1=(sum(R1(:)))./48 %全体数的平均值aver1 =0.0950b=std(R1(:)) %全体数的均方差即标准差b =1.01033、设x=rcost+3t,y=rsint+3,分别令r=2,3,4，画出参数t=0~10区间生成的x~y 曲线。

matlab仿真实例100题Matlab是一种强大的数学软件，广泛应用于科学计算、数据分析和工程仿真等领域。

在学习和使用Matlab的过程中，通过实例的方式进行仿真练习是一种非常有效的学习方法。

下面将给出100个Matlab仿真实例题目，帮助读者更好地掌握Matlab的使用。

1. 编写一个程序，计算并输出1到100之间所有奇数的和。

2. 编写一个程序，计算并输出1到100之间所有偶数的乘积。

3. 编写一个程序，计算并输出1到100之间所有素数的个数。

4. 编写一个程序，计算并输出1到100之间所有整数的平方和。

5. 编写一个程序，计算并输出1到100之间所有整数的立方和。

6. 编写一个程序，计算并输出1到100之间所有整数的阶乘和。

7. 编写一个程序，计算并输出1到100之间所有整数的倒数和。

8. 编写一个程序，计算并输出1到100之间所有整数的平均值。

9. 编写一个程序，计算并输出1到100之间所有整数的中位数。

10. 编写一个程序，计算并输出1到100之间所有整数的标准差。

11. 编写一个程序，计算并输出1到100之间所有整数的方差。

12. 编写一个程序，计算并输出1到100之间所有整数的最大值。

13. 编写一个程序，计算并输出1到100之间所有整数的最小值。

15. 编写一个程序，计算并输出1到100之间所有整数的平方根和。

16. 编写一个程序，计算并输出1到100之间所有整数的立方根和。

17. 编写一个程序，计算并输出1到100之间所有整数的对数和。

18. 编写一个程序，计算并输出1到100之间所有整数的指数和。

19. 编写一个程序，计算并输出1到100之间所有整数的正弦和。

20. 编写一个程序，计算并输出1到100之间所有整数的余弦和。

21. 编写一个程序，计算并输出1到100之间所有整数的正切和。

22. 编写一个程序，计算并输出1到100之间所有整数的双曲正弦和。

23. 编写一个程序，计算并输出1到100之间所有整数的双曲余弦和。

matlab编程经典例题
以下是一些经典的 MATLAB 编程例题：
1. 编写一个程序，计算一个数列的前 N 个斐波那契数（斐波那契数列是指前两个数为 1，后续每个数是前两个数之和）。

2. 编写一个程序，计算一个数的阶乘。

3. 编写一个程序，计算两个矩阵的乘积。

4. 编写一个程序，找到一个数组中的最大元素。

5. 编写一个程序，检查一个字符串是否是回文。

6. 编写一个程序，为给定的一组数据计算均值、中位数和标准差。

7. 编写一个程序，将一个字符串中的所有元音字母替换成大写字母。

8. 编写一个程序，计算一个数列的前 N 个素数（素数是指只能被 1 和自身整除的数）。

9. 编写一个程序，实现冒泡排序算法，对一个数组进行排序。

10. 编写一个程序，计算一个数的平方根。

以上是一些经典的 MATLAB 编程例题，你可以根据自己的实际需要选择其中的一个或几个进行练习和编程。

MATLAB例题考试及答案例1.1 分别绘制函数和的曲线。

x=-2*pi:pi/180:2*pi;plot(x,2.^(-abs(x)),':',x,sin(x));例1.2 求方程2x5-3x3 +71x2-9x+13=0的全部根。

p=[2,0,-3,71,-9,13];x=roots(p)例1.3 求解线性方程组。

a=[2,3,-1;8,2,3;45,3,9];b=[2;4;23];x=inv(a)*b例1.4 求积分quad('x.*log(1+x)',0,1)例2.2 利用M文件建立MYMAT矩阵。

(1)启动有关编辑程序或MATLAB文本编辑器(见第4章)，并输入待建矩阵：MYMAT=[101,102,103,104,105,106,107,108,109;201,202,203,204,205,206,207,208,209;301,302,303,304,305,306,307,308,309]例2.3 建立5阶方阵A，判断A的元素是否能被3整除。

A =[24,35,13,22,63;23,39,47,80,80; ...90,41,80,29,10;45,57,85,62,21;37,19,31,88,76]P=rem(A,3)==0例2.5 建立矩阵A，然后找出在[10，20]区间的元素的位置。

(1) 建立矩阵A。

A=[4,15,-45,10,6;56,0,17,-45,0](2) 找出大于4的元素的位置。

find(A>=10 & A<=20)ans =367例2.6 建立一个字符串向量，然后对该向量做如下处理：(1)取第1~5个字符组成的子字符串。

(2)将字符串倒过来重新排列。

(3)将字符串中的小写字母变成相应的大写字母，其余字符不变。

(4)统计字符串中小写字母的个数。

命令如下：ch='ABc123d4e56Fg9';subch=ch(1:5)subch =ABc12revch=ch(end:-1:1)revch =9gF65e4d321cBAk=find(ch>='a'&ch<='z');ch(k)=ch(k)-('a'-'A');char(ch)ans =ABC123D4E56FG9length(k)ans =4例3.2 建立随机矩阵：(1) 在区间[20,50]内均匀分布的5阶随机矩阵。

【例】水资源系统规划调度常应用系统分析方法处理，以一个水资源分配问题为例，讨论线性规划问题。

例：有甲、乙两个水库同时给A、B、C三个城市供水，甲水库的日供水量为28万m3/d，乙水库的日供水量为35万m3/d，三个城市的日需水量分别为A≥10万m3/d，B≥15万m3/d，C≥20 万m3/d。

由于水库与各城市的距离不等，输水方式不同，因此单位水费也不同。

各单位水费分别为c11＝2000元/万m3、c12＝3000元/万m3、c13＝4000元/万m3、c21＝4500元/万m3、c22＝3500元/万m3、c23＝3000元/万m3。

试作出在满足对三个城市供水的情况下，输水费用最小的方案。

设甲水库向三城市日供水量分别为x ll、x12、x13，乙水库向三城市日供水量分别为x2l、x22、x23。

建立约束条件：x11 + x21 ≥10x12 + x22 ≥15x13 + x23 ≥20x11 + x12 + x13 ≤28x21 + x22 + x23 ≤35x11，x12，x13，x21，x22，x23，≥0目标函数：fmin=c11x11+c12x12+c13x13+c21x21+c22x22+c23x23这样的问题单纯求解是非常繁琐的，而MLTLAB求解是十分简单的，只要在命令行输入：》f=[0.2 0.3 0.4 0.45 0.35 0.3]’；》A=[-1 0 0 -1 0 0；0 -1 0 0 -1 0；0 0 -1 0 0 -1；1 1 1 0 0 0；0 0 0 1 1 1]；》B=[-10 -15 -20 28 35]；》lb=zeros（6，1）；》[X，Zmin]=linprog(f，A，B，[]，[]，lb,[])最后得出x=[10 15 0 0 0 20]万m3，Zmin=12.5万元。

填空题1. MATLAB于1984年由美国Mathworks公司推出，其后每年更新（两次。

2. MATLAB是一种以（矩阵）运算为基础的交互式程序设计语言。

3. MATLAB具有卓越的数值计算能力和符号计算、文字处理、可视化建模仿真和实时控制等众多功能，其每个变量代表一个（矩阵），每个元素都看作（复数）。

4.通过命令（help）、（lookfor），可以查找所有命令或函数的使用方法。

5.执行语句a=1:2:10，得到的一维数组是（1 3 5 7 9）.6.执行语句b=linspace（1,10,10）后，一维数组b包含（10）个元素，最大值是10）7.函数rem（）的功能是取（余）数。

8.若p=[1 0 0;1 1 0],则p|〜p=（[1 1 1;1 1 1]）.（注：填空时请用本题的p的方式表示结果）9.若p=[1 0 0;1 1 0],则all（p）=（[1 0 0]）.10.矩阵的加减运算，要求相加减的矩阵阶数相同。

若A=[1 2 3 4；2 3 1 8]，则执行语句：[n,m]=size（A），则n=（2 ）,m=（4 ）.11.对于一维矩阵，求其长度的函数是（length（））.12.数组和数组之间的运算，尤其是对于乘除运算和乘方运算，如果采用点方式进行计算，表明是数组的（元素）之间的运算关系。

13.求矩阵运算A*B时，要求在维度上，A的（列）数与B的（行）数相等。

二、判断题1.MATLAB只有一种数据类型，一种标准的输入输出语句，不需编译，可直接运行。

（对2.MATLAB的特殊常量是一些预选定义好的数值变量。

（对3.MATLAB变量名不区分大小写。

（错4.i是特殊常量。

（对5.NAN是非数。

（对6.MATLAB中所有的变量都表示一个矩阵或一个向量。

（对7.MATLAB中变量不需要先定义后使用，会自动根据实际赋值的类型对变量类型进行定义。

（对8.clc命令可以从内存中删除一个、多个和所有变量。

1、 在MATLAB 中用Jacobi 迭代法讨论线性方程组,1231231234748212515x x x x x x x x x -+=⎧⎪-+=-⎨⎪-++=⎩（1）给出Jacobi 迭代法的迭代方程，并判定Jacobi 迭代法求解此方程组是否收敛。

（2）若收敛，编程求解该线性方程组.解（1）：A=[4 -1 1;4 —8 1;-2 1 5］ %线性方程组系数矩阵A =4 -1 1 4 -8 1 —2 1 5>> D=diag(diag(A)）D =4 0 0 0 —8 0 0 0 5〉〉 L=—tril （A,-1) ％ A 的下三角矩阵L =0 0 0 —4 0 0 2 —1 0〉〉U=-triu(A，1）% A的上三角矩阵U =0 1 —10 0 —10 0 0B=inv（D）*（L+U）% B为雅可比迭代矩阵B =0 0.2500 —0。

25000.5000 0 0.12500。

4000 —0.2000 0〉〉r=eigs(B,1）%B的谱半径r =0。

3347 〈1Jacobi迭代法收敛。

(2）在matlab上编写程序如下:A=[4 —1 1;4 -8 1;—2 1 5]；〉〉b=［7 —21 15］'；>〉x0=［0 0 0]’;〉〉［x,k］=jacobi（A,b，x0，1e—7)x =2。

00004.00003。

0000k =17附jacobi迭代法的matlab程序如下：function [x,k］=jacobi（A,b，x0，eps)% 采用Jacobi迭代法求Ax=b的解％A为系数矩阵％b为常数向量％x0为迭代初始向量％eps为解的精度控制max1= 300; %默认最多迭代300，超过300次给出警告D=diag（diag（A）)；％求A的对角矩阵L=-tril(A，—1); %求A的下三角阵U=—triu（A,1); %求A的上三角阵B=D\(L+U);f=D\b;x=B＊x0+f；k=1；%迭代次数while norm（x-x0）>=epsx0=x;x=B＊x0+f；k=k+1;if（k〉=max1)disp(’迭代超过300次，方程组可能不收敛’）；return；endend2、设有某实验数据如下：（1)在MATLAB中作图观察离散点的结构,用多项式拟合的方法拟合一个合适的多项式函数；（2）在MATLAB中作出离散点和拟合曲线图。