上海市奉贤区2009年高考模拟考试数学试卷理科2009.3

2009年高考模拟考试 数学（理）参考答案及评分标准一、选择题：每小题5分，共50分。

————（其中1为原创，10选自2008年江苏盐城中学，其它为改编）二、填空题：每小题4分，共28分11．1- 12．14 13．4 14．00221x x y y a b+= 15． 112-或 16．273a π 17． ln 2 ————（其中14、15题为原创，其它为改编）三、解答题：本大题共5小题72分 18.解：（1）2()sin(2)sin(2)2cos 66f x x x x ππ=++-+sin 2coscos 2sinsin 2coscos 2sincos 216666x x x x x ππππ=++-++……3分12cos 2sin 3++=x x 1)62sin(2++=πx ………………6分312)(max =+=∴x fππωπ===22||2T…………………………8分 （2）由()2f x ≥ 得2sin(2)126x π++≥21)62sin(≥+∴πx πππππ6526262+≤+≤+∴k x k …………12分)(3Z k k x k ∈+≤≤∴πππ2)(≥∴x f 的x 的取值范围是},3|{Z k k x k x ∈+≤≤πππ…………14分————（此题根据必修四第三章复习题9、10、11、12改编）19.解：（1） 甲胜的概率为10.50.30.2--=，甲输的概率（即乙胜）为0.3……2分∴甲的得分ξ可取0，1，2，3，4，5，6 3(0)0.30.027P ξ===223(1)0.30.50.135P C ξ==⨯= 221233(2)0.30.20.30.50.279P C C ξ==⨯+⨯= 333(3)0.30.50.20.50.305P A ξ==⨯⨯+=122233(4)0.30.20.50.20.186P C C ξ==⨯+⨯=123(5)0.50.20.06P C ξ==⨯= 3(6)0.20.008P ξ=== ξ∴的分布列为8分（2）∵f x （）在（0，2）上单调递减 ∴242ξξ≥≥对称轴，即…………………………11分∴()(4)0.1860.060.0080.254P A P ξ=≥=++=……………………14分————（此题为改编）20.解：（1）∵- ()-()-1x mf x f x e '∞+∞=在（，）上连续，令.,0)(m x x f =='得……………………2分;1)()(.)(,,.0)(,1,),(;0)(,1,),(min m m f x f x f m x x f e m x x f e m x m x m x -==∴=>'>+∞∈<'<-∞∈--取极小值也是最小值时当所以时当时当由①知f （x ）无最大值.……………………6分（2）函数f （x ）在[m ，2m]上连续，,02)(,1,2)(,2)(,2)2(>->'∴>-='-=-=e m g m e m g m e m g m e m f m m m 则令而∴()1g m +∞在（，）上递增。

上海市奉贤区2009年高考模拟考试数学试卷（理工类）2009.03（完卷时间：120分钟 满分：150分）一、填空题：（共55分，每小题5分）1、方程233log (10)1log x x -=+的解是 。

2、不等式1223x->的解集为 。

3、已知复数z ＝－i 为纯虚数，则实数a= 。

4、在极坐标系中，O 是极点，设点)6,4(πA ，)65,2(πB ，则三角形OAB 的面积为 5、若51x a ⎛⎫- ⎪⎝⎭的二项展开式中含3x 项的系数是80，则实数a 的值为 ．6、在1，2，3，4，5这五个数字中任取不重复的3个数字组成一个三位数，则组成的三位数是奇数的概率是 。

（用分数表示）7、关于函数()x x x f 2arcsin =有下列命题：①()x f 的定义域是R ；②()x f 是偶函数；③()x f 在定义域内是增函数；④()x f 的最大值是4π，最小值是0。

其中正确的命题是 。

（写出你所认为正确的所有命题序号）8、已知直角三角形的两直角边长分别为3cm 和4cm ，则以斜边为轴旋转一周所得几何体的表面积为 。

9、已知各项均为正数的等比数列}{n a 的首项11=a ，公比为q ，前n 项和为n S ，若1lim1=+∞→nn n S S ，则公比为q 的取值范围是 。

10、设实数y x ,满足1)1(22=-+y x ，若对满足条件y x ,，不等式0≥++c y x 恒成立，则c 的取值范围是 。

11、现有31行67列表格一个，每个小格都只填1个数，从左上角开始，第一行依次为1，2，…67；第二行依次为68，69…134；…依次把表格填满。

现将此表格的数按另一方式填写，从左上角开始，第一列从上到下依次为1，2…，31；第二列从上到下依次为32，33，…，62；…依次把表格填满。

对于上述两种填法，在同一小格里两次填写的数相同，这样的小格在表格中共有_________个。

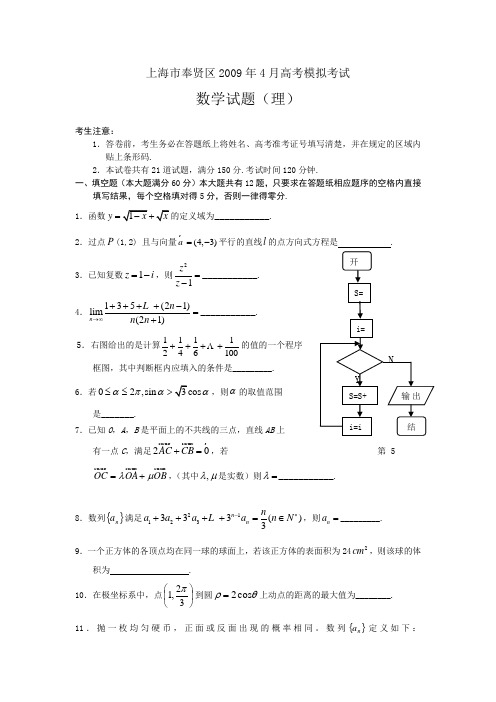
第5上海市奉贤区2009年4月高考模拟考试数学试题（理）考生注意：1．答卷前，考生务必在答题纸上将姓名、高考准考证号填写清楚，并在规定的区域内贴上条形码.2．本试卷共有21道试题，满分150分.考试时间120分钟.一、填空题（本大题满分60分）本大题共有12题，只要求在答题纸相应题序的空格内直接填写结果，每个空格填对得5分，否则一律得零分. 1．函数y =___________.2．过点P (1,2) 且与向量a r(4,3)=-平行的直线l 的点方向式方程是 .3．已知复数1z i =-，则21z z =-___________. 4．135(21)lim(21)n n n n →∞++++-=+L ___________.5．右图给出的是计算1001614121++++Λ的值的一个程序 框图，其中判断框内应填入的条件是_________. 6．若02,sin απαα≤≤>，则α的取值范围是_______.7．已知O ，A ，B 是平面上的不共线的三点，直线AB 上有一点C ，满足20AC CB +=u u u r u u u r r，若OC =u u u r OA OB λμ+u u u r u u u r ，（其中,λμ是实数）则λ=___________.8．数列{}n a 满足21123333()3n n na a a a n N -*++++=∈L ，则n a =_________. 9．一个正方体的各顶点均在同一球的球面上，若该正方体的表面积为242cm ，则该球的体积为 . 10．在极坐标系中，点⎪⎭⎫⎝⎛32,1π到圆θρcos 2=上动点的距离的最大值为________. 11．抛一枚均匀硬币，正面或反面出现的概率相同。

数列{}n a 定义如下：⎩⎨⎧-=次投掷出现反面第次投掷出现正面第n n a n 11，设∈++++=n a a a a S n n (321ΛN*)，那么28=S 的概率是______.12．设全集{}(,),U x y x y R =∈，集合{}(,)cos sin 20,,,A x y x y x y R θθθ=+-=∈，则在直角平面上集合U C A 内所有元素的对应点构成的图形的面积等于______. 二．选择题（本大题满分16分）本大题共有4题，每题都给出四个结论，其中有且只有一个结论是正确的，必须把答题纸上相应题序内的正确结论代号涂黑，选对得 4分，否则一律得零分.13．200辆汽车通过某一段公路时的时速的频率分布直方图如右图所示，时速在[50,60)的汽车大约有（ ） A ．30辆 B ．40辆 C ．60辆D ．80辆14．方程)(122R a ay x ∈=+所表示的曲线不可能是（ ） A ．抛物线 B ．圆C ．双曲线D ．直线15．“18a =”是“对任意的正数x ，21ax x+≥”的（ ） A ．充分不必要条件 B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件16．设函数()()(),F x f x f x x R =+-∈在区间,2ππ⎡⎤--⎢⎥⎣⎦上单调递增，现将()F x 的图象向右平移π个单位得到函数()G x ，则函数()G x 的单调递减区间必定是（ ）A ．,02π⎡⎤-⎢⎥⎣⎦ B ．,2ππ⎡⎤⎢⎥⎣⎦C ．3,2ππ⎡⎤⎢⎥⎣⎦D ．3,22ππ⎡⎤⎢⎥⎣⎦三．解答题（本大题满分74分）本大题共有5题，解答下列各题必须在答题纸的规定区域（对应的题号．．．．．）内写出必要的步骤. 17．(本题满分12分) 本题共有2个小题，第1小题满分6分，第2小题满分6分.如图所示为电流强度i （安培）随时间t （秒）变化的关系式是：[)sin ,0,i A t t ω=∈+∞（其中A >0）的图象。

2009年全国普通高等学校招生统一考试上海 数学试卷一．填空题 （本大题满分56分）本大题有14题，考生应在答题纸相应编号的空格内直接写结果，每个空格填对得4分，否则一律得零分1． 若复数 z 满足z (1+i) =1-i (i 是虚数单位)，则其共轭复数z =__________________ . 2． 已知集合{}|1A x x = ，{}|B x x a = ，且A BR ?，则实数a 的取值范围是______________________ .3． 若行列式417xx 5 3 8 9中，元素4的代数余子式大于0，则x 满足的条件是________________________ .4．某算法的程序框如右图所示，则输出量y 与输入量x 满足的关系式是____________________________ .5．如图，若正四棱柱1111ABC D A B C D - 的底面边长为2，高为4，则异面直线1BD 与AD 所成角的大小是______________（结果用反三角函数表示）. 6．函数22cos sin 2y x x =+的最小值是_____________________ .7．某学校要从5名男生和2名女生中选出2人作为上海世博会志愿者，若用随机变量ξ表示选出的志愿者中女生的人数，则数学期望E ξ=____________（结果用最简分数表示）.8. 已知三个球的半径1R ，2R ，3R 满足12323R R R +=，则它们的表面积1S ，2S ，3S ，满足的等量关系是___________. 9. 已知1F 、2F 是椭圆2222:1x y C ab+=（a ＞b ＞0）的两个焦点，P 为椭圆C 上一点，且12PF PF ^.若12PF F D 的面积为9，则b =____________. 10. 在极坐标系中，由三条直线0q =，3p q =，cos sin 1r q r q +=围成图形的面积是________.11.当01x ＃时，不等式sin2x kx p ³成立，则实数k 的取值范围是_______________.12．已知函数()sin tan f x x x =+.项数为27的等差数列{}n a 满足22n a p p骣琪?琪桫，，且公差0d ¹.若1227()()()0f a f a f a ++?=，则当k =___________时，()0k f a =.13. 某地街道呈现东—西、南—北向的网格状，相邻街距都为1.两街道相交的点称为格点。

2009年上海市高考数学试卷（理科)一、填空题（共14小题，每小题4分，满分56分）1．若复数z 满足z （1+i ）=1-i （i 是虚数单位），则其共轭复数z =_________． 【测量目标】复数的基本概念;复数代数形式的四则运算. 【考查方式】化简复数等式，求解一个复数的共轭复数. 【难易程度】中等 【参考答案】i【试题解析】设z ＝a ＋b i,则（a ＋b i ）(1+i) =1-i,即a －b ＋（a ＋b )i ＝1－i ，（步骤1）由⎩⎨⎧-=+=-11b a b a ,解得a ＝0，b ＝－1，所以z ＝－i ，z ＝i,故答案为i ．（步骤2) 2．已知集合A ={x |x1｝，B =｛x |xa ｝,且A B =R ，则实数a 的取值范围是_________．【测量目标】集合的基本运算.【考查方式】给出两个集合,已知集合间的关系,运用数轴法求解集合中未知参数的取值范围． 【难易程度】容易 【参考答案】a1【试题解析】因为A B =R ,画数轴可知，实数a 必须在点1上或在1的左边，所以，有a 1。

第2题图3．若行列式4513789xx 中，元素4的代数余子式大于0,则x 满足的条件是_________．【测量目标】矩阵初步.【考查方式】根据代数余子式的概念，列出关于x 的不等式求出取值范围. 【难易程度】中等【参考答案】x ＞83【试题解析】依题意，得： (-1）2⨯(9x -24）＞0，解得：83x >，故答案为：x ＞83. 4．某算法的程序框如下图所示,则输出量y 与输入量x 满足的关系式是_________．第4题图【测量目标】选择结构程序框图.【考查方式】给出程序框图，按照程序框图的执行流程分析循环过程，判断输入值与输出值之间的关系。

【难易程度】容易 【参考答案】2,12,1xx x y x->⎧=⎨⎩【试题解析】根据流程图所示的顺序，程序的作用是分段函数的函数值．其中输出量y 与输入量x 满足的关系式是2,12,1x x x y x ->⎧=⎨⎩，故答案为：2,12,1xx x y x ->⎧=⎨⎩. 5．如图,若正四棱柱ABCD -A 1B 1C 1D 1的底面边长为2，高为4,则异面直线BD 1与AD 所成角的大小是_________。

2009年上海市高考数学试卷（理科）参考答案与试题解析一、填空题（共14小题，每小题4分，满分56分）1．（4分）（2009•上海）若复数z满足z（1+i）=1﹣i（I是虚数单位），则其共轭复数=i．【考点】复数的基本概念；复数代数形式的乘除运算．【专题】计算题．【分析】本题考查的知识点是共轭复数的定义，由复数z满足z（1+i）=1﹣i，我们可能使用待定系数法，设出z，构造方程，求出z值后，再根据共轭复数的定义，计算【解答】解：设z=a+bi，则∵（a+bi）（1+i）=1﹣i，即a﹣b+（a+b）i=1﹣i，由，解得a=0，b=﹣1，所以z=﹣i，=i，故答案为i．【点评】求复数的共轭复数一般步骤是：先利用待定系数法设出未知的向量，根据已知条件构造复数方程，根据复数相等的充要条件，转化为一个实数方程组，进而求出求知的复数，再根据共轭复数的定义，求出其共轭复数．2．（4分）（2009•上海）已知集合A={x|x≤1}，B={x|x≥a}，且A∪B=R，则实数a的取值范围是a≤1．【考点】集合关系中的参数取值问题．【专题】集合．【分析】利用数轴，在数轴上画出集合，数形结合求得两集合的并集．【解答】解：∵A={x|x≤1}，B={x|x≥a}，且A∪B=R，如图，故当a≤1时，命题成立．故答案为：a≤1．【点评】本题属于以数轴为工具，求集合的并集的基础题，也是高考常会考的题型．3．（4分）（2009•上海）若行列式中，元素4的代数余子式大于0，则x满足的条件是x＞且x≠4．【考点】三阶矩阵．【专题】计算题．【分析】根据3阶行列式D的元素a ij的余子式M ij附以符号（﹣1）i+j后，叫做元素a ij的代数余子式，所以4的余子式加上（﹣1）1+1即为元素4的代数余子式，让其大于0列出关于x的不等式，求出不等式的解集即可得到x的范围．【解答】解：依题意得，（﹣1）2＞0，即9x﹣24＞0，解得x＞，且x≠4，故答案为：x＞且x≠4【点评】此题考查学生掌握三阶矩阵的代数余子式的定义，是一道基础题．4．（4分）（2009•上海）某算法的程序框如下图所示，则输出量y与输入量x满足的关系式是．【考点】程序框图．【分析】根据流程图所示的顺序，逐框分析程序中各变量、各语句的作用可知：该程序的作用是根据输入x值的不同，根据不同的式子计算函数值．即求分段函数的函数值．【解答】解：根据流程图所示的顺序，程序的作用是分段函数的函数值．其中输出量y与输入量x满足的关系式是故答案为：【点评】根据流程图（或伪代码）写程序的运行结果，是算法这一模块最重要的题型，其处理方法是：：①分析流程图（或伪代码），从流程图（或伪代码）中既要分析出计算的类型，又要分析出参与计算的数据（如果参与运算的数据比较多，也可使用表格对数据进行分析管理）⇒②建立数学模型，根据第一步分析的结果，选择恰当的数学模型③解模．5．（4分）（2009•上海）如图，若正四棱柱ABCD﹣A1B1C1D1的底面边长为2，高为4，则异面直线BD1与AD所成角的大小是arctan（结果用反三角函数值表示）．【考点】异面直线及其所成的角．【专题】计算题．【分析】先通过平移将两条异面直线平移到同一个起点，得到的锐角或直角就是异面直线所成的角，在直角三角形中求出正切值，再用反三角函数值表示出这个角即可．【解答】解：先画出图形将AD平移到BC，则∠D1BC为异面直线BD1与AD所成角，BC=2，D1C=，tan∠D1BC=，∴∠D1BC=arctan，故答案为arctan．【点评】本题主要考查了异面直线及其所成的角，以及解三角形的应用，属于基础题．6．（4分）（2009•上海）函数y=2cos2x+sin2x的最小值是．【考点】三角函数的最值．【专题】计算题．【分析】先利用三角函数的二倍角公式化简函数，再利用公式化简三角函数，利用三角函数的有界性求出最小值．【解答】解：y=2cos2x+sin2x=1+cos2x+sin2x=1+=1+当=2k，有最小值1﹣故答案为1﹣【点评】本题考查三角函数的二倍角余弦公式将三角函数降幂、利用公式化简三角函数．7．（4分）（2009•上海）某学校要从5名男生和2名女生中选出2人作为上海世博会志愿者，若用随机变量ξ表示选出的志愿者中女生的人数，则数学期望Eξ（结果用最简分数表示）．【考点】离散型随机变量的期望与方差．【专题】计算题．【分析】用随机变量ξ表示选出的志愿者中女生的人数，ξ可取0，1，2，结合变量对应的事件写出分布列当ξ=0时，表示没有选到女生；当ξ=1时，表示选到一个女生；当ξ=2时，表示选到2个女生，求出期望．【解答】解：用随机变量ξ表示选出的志愿者中女生的人数，ξ可取0，1，2，当ξ=0时，表示没有选到女生；当ξ=1时，表示选到一个女生；当ξ=2时，表示选到2个女生，∴P（ξ=0）==，P（ξ=1）=，P（ξ=2）=，∴Eξ=0×=．故答案为：【点评】本题考查离散型随机变量的分布列和期望，这是近几年经常出现的一个问题，可以作为解答题出现，考查的内容通常是以分布列和期望为载体，有时要考查其他的知识点．8．（4分）（2009•上海）已知三个球的半径R1，R2，R3满足R1+2R2=3R3，则它们的表面积S1，S2，S3，满足的等量关系是．【考点】球的体积和表面积．【专题】计算题．【分析】表示出三个球的表面积，求出三个半径，利用R1+2R2=3R3，推出结果．【解答】解：因为S1=4πR12，所以，同理：，即R1=，R2=，R3=，由R1+2R2=3R3，得故答案为：【点评】本题考查球的表面积，考查计算能力，是基础题．9．（4分）（2009•上海）已知F1、F2是椭圆C：（a＞b＞0）的两个焦点，P为椭圆C上一点，且．若△PF1F2的面积为9，则b=3．【考点】椭圆的应用；椭圆的简单性质．【专题】圆锥曲线的定义、性质与方程．【分析】由已知得|PF1|+|PF2|=2a，=4c2，，由此能得到b的值．【解答】解：∵F1、F2是椭圆C：（a＞b＞0）的两个焦点，P为椭圆C上一点，且．∴|PF1|+|PF2|=2a，=4c2，，∴（|PF1|+|PF2|）2=4c2+2|PF1||PF2|=4a2，∴36=4（a2﹣c2）=4b2，∴b=3．故答案为3．【点评】主要考查椭圆的定义、基本性质和平面向量的知识．10．（4分）（2009•上海）在极坐标系中，由三条直线θ=0，，ρcosθ+ρsinθ=1围成图形的面积等于．【考点】简单曲线的极坐标方程；定积分．【专题】计算题．【分析】三条直线化为直角坐标方程，求出三角形的边长，然后求出图形的面积．【解答】解：三条直线θ=0，，ρcosθ+ρsinθ=1的直角坐标方程分别为：y=0，y=x，x+y=1，所以它们的交点坐标分别为O（0，0），A（1，0），B（，），OB==，由三条直线θ=0，，ρcosθ+ρsinθ=1围成图形的面积S==．故答案为：．【点评】本题考查极坐标与直角坐标的互化，三角形的面积的求法，考查计算能力．11．（4分）（2009•上海）当时，不等式sinπx≥kx恒成立．则实数k的取值范围是k≤2．【考点】函数恒成立问题．【专题】数形结合．【分析】要使不等式sinπx≥kx恒成立，设m=sinπx，n=kx，利用图象得到k的范围即可．【解答】解：设m=sinπx，n=kx，x∈[0，]．根据题意画图得：m≥n恒成立即要m的图象要在n图象的上面，当x=时即πx=时相等，所以此时k==2，所以k≤2故答案为k≤2【点评】考查学生利用数形结合的数学思想解决问题的能力，理解函数恒成立时取条件的能力．12．（4分）（2009•上海）已知函数f（x）=sinx+tanx，项数为27的等差数列{a n}满足a n∈（﹣），且公差d≠0，若f（a1）+f（a2）+…f（a27）=0，则当k=14时，f（a k）=0．【考点】函数奇偶性的性质．【专题】计算题；压轴题．【分析】本题考查的知识点是函数的奇偶性及对称性，由函数f（x）=sin x+tan x，项数为27的等差数列{a n}满足a n∈（﹣），且公差d≠0，若f（a1）+f（a2）+…f（a27）=0，我们易得a1，a2，…，a27前后相应项关于原点对称，则f（a14）=0，易得k值．【解答】解：因为函数f（x）=sinx+tanx是奇函数，所以图象关于原点对称，图象过原点．而等差数列{a n}有27项，a n∈（）．若f（a1）+f（a2）+f（a3）+…+f（a27）=0，则必有f（a14）=0，所以k=14．故答案为：14【点评】代数的核心内容是函数，函数的定义域、值域、性质均为高考热点，所有要求同学们熟练掌握函数特别是基本函数的图象和性质，并能结合平移、对称、伸缩、对折变换的性质，推出基本函数变换得到的函数的性质．13．（4分）（2009•上海）某地街道呈现东﹣西、南﹣北向的网格状，相邻街距都为1．两街道相交的点称为格点．若以互相垂直的两条街道为轴建立直角坐标系，现有下述格点（﹣2，2），（3，1），（3，4），（﹣2，3），（4，5），（6，6）为报刊零售点．请确定一个格点（除零售点外）（3，3）为发行站，使6个零售点沿街道到发行站之间路程的和最短．【考点】两点间距离公式的应用．【专题】直线与圆．【分析】设发行站的位置为（x，y），则可利用两点间的距离公式表示出零售点到发行站的距离，进而求得在（3，3）处z取得最小值．【解答】解：设发行站的位置为（x，y），6个零售点到发行站的距离为Z，则z=|x+2|+|y﹣2|+|x﹣3|+|y﹣1|+|x﹣3|+|y﹣4|+|x+1|+|y﹣3|+|x﹣4|+|y﹣5|+|x﹣6|+|y﹣6|=|x+2|+|x﹣3|+|x﹣3|+|x+1|+|x﹣4|+|x﹣6|+|y﹣2|+|y﹣1|+|y﹣4|+|y﹣3|+|y﹣5|+|y﹣6|x=3，3≤y＜4时，取最小值，∴在（3，3）处z取得最小值．故答案为（3，3）．【点评】本题主要考查了两点间的距离公式的应用．考查了学生创造性思维能力和逻辑思维能力．14．（4分）（2009•上海）将函数（x∈[0，6]）的图象绕坐标原点逆时针方向旋转角θ（0≤θ≤α），得到曲线C．若对于每一个旋转角θ，曲线C都是一个函数的图象，则α的最大值为arctan．【考点】旋转变换．【专题】计算题；压轴题．【分析】先画出函数（x∈[0，6]）的图象，然后根据由图可知当此圆弧绕坐标原点逆时针方向旋转角大于∠MAB时，曲线C都不是一个函数的图象，求出此角即可．【解答】解：先画出函数（x∈[0，6]）的图象这是一个圆弧，圆心为M（3，﹣2）由图可知当此圆弧绕坐标原点逆时针方向旋转角大于∠MAB时，曲线C都不是一个函数的图象∴∠MAB=arctan故答案为：arctan【点评】本题主要考查了旋转变换，同时考查了数形结合的思想和分析问题解决问题的能力，属于基础题．二、选择题（共4小题，每小题4分，满分16分）15．（4分）（2009•上海）“﹣2≤a≤2”是“实系数一元二次方程x2+ax+1=0有虚根”的（）A．必要不充分条件B．充分不必要条件C．充要条件 D．既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断．【分析】实系数一元二次方程x2+ax+1=0有虚根⇒△=a2﹣4＜0⇒﹣2＜a＜2，由此入手能够作出正确选择．【解答】解：∵实系数一元二次方程x2+ax+1=0有虚根，∴△=a2﹣4＜0，解得﹣2＜a＜2，∴“﹣2≤a≤2”是“﹣2＜a＜2”的必要不充分条件，故选A．【点评】本题考查必要条件、充分条件和充要条件的应用，解题时要认真审题，仔细解答．16．（4分）（2009•上海）若事件E与F相互独立，且P（E）=P（F）=，则P（E∩F）的值等于（）A．0 B．C．D．【考点】相互独立事件的概率乘法公式．【分析】本题考查的知识点是相互独立事件的概率乘法公式，由相互独立事件的概率计算公式，我们易得P（E∩F）=P（E）•P（F），将P（E）=P（F）=代入即可得到答案．【解答】解：P（E∩F）=P（E）•P（F）=×=．故选B．【点评】相互独立事件的概率计算公式：P（E∩F）=P（E）•P（F），P（E∪F）=P（E）+P（F）．17．（4分）（2009•上海）有专业机构认为甲型N1H1流感在一段时间没有发生大规模群体感染的标志为“连续10天，每天新增疑似病例不超过15人”．根据过去10天甲、乙、丙、丁四地新增疑似病例数据，一定符合该标志的是（）A．甲地：总体均值为3，中位数为4B．乙地：总体均值为1，总体方差大于0C．丙地：中位数为2，众数为3D．丁地：总体均值为2，总体方差为3【考点】众数、中位数、平均数；极差、方差与标准差．【专题】压轴题．【分析】平均数和方差都是重要的数字特征，是对总体的一种简单的描述，平均数描述集中趋势，方差描述波动大小．【解答】解：假设连续10天，每天新增疑似病例的人数分别为x1，x2，x3，…x10．并设有一天超过15人，不妨设第一天为16人，根据计算方差公式有s2=[（16﹣5）2+（x2﹣5）2+（x3﹣5）2+…+（x10﹣5）2]＞12，说明乙地连续10天，每天新增疑似病例的人数都不超过15人．故选：B．【点评】根据题意可知本题主要考查用数字特征估计总体，属于基础题．18．（4分）（2009•上海）过圆C：（x﹣1）2+（y﹣1）2=1的圆心，作直线分别交x、y正半轴于点A、B，△AOB被圆分成四部分（如图），若这四部分图形面积满足S|+S IV=S||+S|||则直线AB有（）A．0条B．1条C．2条D．3条【考点】直线与圆的位置关系．【专题】综合题；压轴题；数形结合．【分析】由圆的方程得到圆心坐标和半径，根据四部分图形面积满足S|+S IV=S||+S|||，得到S IV﹣S II=SⅢ﹣S I，第II，IV部分的面积是定值，所以三角形FCB减去三角形ACE的面积为定值即SⅢ﹣S I为定值，所以得到满足此条件的直线有且仅有一条，得到正确答案．【解答】解：由已知，得：S IV﹣S II=SⅢ﹣S I，由图形可知第II，IV部分的面积分别为S正方形OECF﹣S扇形ECF=1﹣和S扇形ECF=，所以，S IV﹣S II为定值，即SⅢ﹣S I为定值，当直线AB绕着圆心C移动时，只可能有一个位置符合题意，即直线AB只有一条．故选B．【点评】此题考查学生掌握直线与圆的位置关系，会求三角形、正方形及扇形的面积，是一道综合题．三、解答题（共5小题，满分78分）19．（14分）（2009•上海）如图，在直三棱柱ABC﹣A1B1C1中，AA1=BC=AB=2，AB⊥BC，求二面角B1﹣A1C﹣C1的大小．【考点】向量在几何中的应用；与二面角有关的立体几何综合题．【专题】计算题；向量法．【分析】建立空间直角坐标系，求出2个平面的法向量的坐标，设二面角的大小为θ，显然θ为锐角，设2个法向量的夹角φ，利用2个向量的数量积可求cosφ，则由cosθ=|cosφ|求出二面角的大小θ．【解答】解：如图，建立空间直角坐标系．则A（2，0，0），C（0，2，0），A1（2，0，2），B1（0，0，2），C1（0，2，2），设AC的中点为M，∵BM⊥AC，BM⊥CC1．∴BM⊥平面A1C1C，即=（1，1，0）是平面A1C1C的一个法向量．设平面A1B1C的一个法向量是n=（x，y，z）．=（﹣2，2，﹣2），=（﹣2，0，0），∴令z=1，解得x=0，y=1．∴n=（0，1，1），设法向量n与的夹角为φ，二面角B1﹣A1C﹣C1的大小为θ，显然θ为锐角．∵cosθ=|cosφ|==，解得：θ=．∴二面角B1﹣A1C﹣C1的大小为．【点评】本题考查利用向量求二面角的大小的方法，设二面角的大小为θ，2个平面法向量的夹角φ，则θ和φ相等或互补，这两个角的余弦值相等或相反．20．（16分）（2009•上海）有时可用函数f（x）=，描述学习某学科知识的掌握程度．其中x表示某学科知识的学习次数（x∈N*），f（x）表示对该学科知识的掌握程度，正实数a与学科知识有关．（1）证明：当x≥7时，掌握程度的增长量f（x+1）﹣f（x）总是下降；（2）根据经验，学科甲、乙、丙对应的a的取值区间分别为（115，121]，（121，127]，（127，133]．当学习某学科知识6次时，掌握程度是85%，请确定相应的学科．【考点】分段函数的应用．【专题】应用题；探究型；数学模型法．【分析】（1）x≥7时，作差求出增长量f（x+1）﹣f（x），研究其单调性知，差是一个减函数，故掌握程度的增长量总是下降、（2）学习某学科知识6次时，掌握程度是85%，故得方程由此方程解出a的值即可确定相应的学科．【解答】证明：（1）当x≥7时，而当x≥7时，函数y=（x﹣3）（x﹣4）单调递增，且（x﹣3）（x﹣4）＞0故函数f（x+1）﹣f（x）单调递减当x≥7时，掌握程度的增长量f（x+1）﹣f（x）总是下降（2）由题意可知整理得解得（13分）由此可知，该学科是乙学科..（14分）【点评】本题是分段函数在实际问题中的应用，在实际问题中，分段函数是一个很重要的函数模型．21．（16分）（2009•上海）已知双曲线，设直线l过点，（1）当直线l与双曲线C的一条渐近线m平行时，求直线l的方程及l与m的距离；（2）证明：当k＞时，在双曲线C的右支上不存在点Q，使之到直线l的距离为．【考点】双曲线的简单性质．【专题】计算题；证明题．【分析】（1）先求出双曲线的渐近线方程，进而可得到直线l的斜率，然后根据直线l过点求出直线l的方程，再由平行线间的距离公式可求直线l的方程及l与m 的距离．（2）设过原点且平行于l的直线方程利用直线与直线的距离求得l与b的距离，当k＞时，可推断出，利用双曲线的渐近线方程可知双曲线C的右支在直线b的右下方，进而推断出双曲线C的右支上的任意点到直线l的距离大于，进而可知故在双曲线C的右支上不存在点Q（x0，y0）到到直线l的距离为．【解答】解：（1）双曲线C的渐近线，即∴直线l的方程∴直线l与m的距离．（2）设过原点且平行于l的直线b：kx﹣y=0，则直线l与b的距离d=，当时，．又双曲线C的渐近线为，∴双曲线C的右支在直线b的右下方，∴双曲线C的右支上的任意点到直线l的距离大于．故在双曲线C的右支上不存在点Q（x0，y0）到到直线l的距离为．【点评】本题主要考查了双曲线的简单性质．考查了学生综合分析问题和解决问题的能力．22．（16分）（2009•上海）已知函数y=f（x）的反函数．定义：若对给定的实数a（a≠0），函数y=f（x+a）与y=f﹣1（x+a）互为反函数，则称y=f（x）满足“a和性质”；若函数y=f（ax）与y=f﹣1（ax）互为反函数，则称y=f（x）满足“a积性质”．（1）判断函数g（x）=x2+1（x＞0）是否满足“1和性质”，并说明理由；（2）求所有满足“2和性质”的一次函数；（3）设函数y=f（x）（x＞0）对任何a＞0，满足“a积性质”．求y=f（x）的表达式．【考点】反函数；函数解析式的求解及常用方法．【专题】压轴题；新定义．【分析】（1）先求出g﹣1（x）的解析式，换元可得g﹣1（x+1）的解析式，将此解析式与g （x+1）的作对比，看是否满足互为反函数．（2）先求出f﹣1（x）的解析式，再求出f﹣1（x+2）的解析式，再由f（x+2）的解析式，求出f﹣1（x+2）的解析式，用两种方法得到的f﹣1（x+2）的解析式应该相同，解方程求得满足条件的一次函数f（x）的解析式．（3）设点（x0，y0）在y=f（ax）图象上，则（y0，x0）在函数y=f﹣1（ax）图象上，可得ay0=f （x0）=af（ax0），，即，即满足条件．【解答】解（1）函数g（x）=x2+1（x＞0）的反函数是，∴，而g（x+1）=（x+1）2+1（x＞﹣1），其反函数为，故函数g（x）=x2+1（x＞0）不满足“1和性质”．（2）设函数f（x）=kx+b（x∈R）满足“2和性质”，k≠0．∴，∴，而f（x+2）=k（x+2）+b（x∈R），得反函数，由“2和性质”定义可知，对（x∈R）恒成立．∴k=﹣1，b∈R，即所求一次函数f（x）=﹣x+b（b∈R）．（3）设a＞0，x0＞0，且点（x0，y0）在y=f（ax）图象上，则（y0，x0）在函数y=f﹣1（ax）图象上，故，可得ay0=f（x0）=af（ax0），令ax0=x，则，∴，即．综上所述，，此时，其反函数是，而，故y=f（ax）与y=f﹣1（ax）互为反函数．【点评】本题考查反函数的求法，函数与反函数的图象间的关系，体现了换元的思想，属于中档题．23．（16分）（2009•上海）已知{a n}是公差为d的等差数列，{b n}是公比为q的等比数列．（1）若a n=3n+1，是否存在m、k∈N*，有a m+a m+1=a k？说明理由；（2）找出所有数列{a n}和{b n}，使对一切n∈N*，，并说明理由；（3）若a1=5，d=4，b1=q=3，试确定所有的p，使数列{a n}中存在某个连续p项的和是数列{b n}中的一项，请证明．【考点】等差数列与等比数列的综合；等差数列的性质；数列递推式．【专题】综合题；压轴题；分类讨论；转化思想．【分析】（1）由a m+a m+1=a k，得6m+5=3k+1，，由m、k∈N*，知k﹣2m为整数，所以不存在m、k∈N*，使等式成立．（2）设a n=nd+c，若，对n∈N×都成立，且{b n}为等比数列，则，对n∈N×都成立，由此入手能够导出有a n=c≠0，b n=1，使对一切n∈N×，．（3）a n=4n+1，b n=3n，n∈N*，设a m+1+a m+2++a m+p=b k=3k，p、k∈N*，m∈N．4m+2p+3+，由p、k∈N*，知p=3s，s∈N．由此入手能导出当且仅当p=3s，s∈N，命题成立．【解答】解：（1）由a m+a m+1=a k，得6m+5=3k+1，整理后，可得，∵m、k∈N*，∴k﹣2m为整数，∴不存在m、k∈N*，使等式成立．（2）设a n=nd+c，若，对n∈N×都成立，且{b n}为等比数列，则，对n∈N×都成立，即a n a n+2=qa n+12，∴（dn+c）（dn+2d+c）=q（dn+d+c）2，对n∈N×都成立，∴d2=qd2（i）若d=0，则a n=c≠0，∴b n=1，n∈N*．（ii）若d≠0，则q=1，∴b n=m（常数），即=m，则d=0，矛盾．综上所述，有a n=c≠0，b n=1，使对一切n∈N×，．（3）a n=4n+1，b n=3n，n∈N*，设a m+1+a m+2++a m+p=b k=3k，p、k∈N*，m∈N．，∴，∵p、k∈N*，∴p=3s，s∈N取k=3s+2，4m=32s+2﹣2×3s﹣3=（4﹣1）2s+2﹣2×（4﹣1）s﹣3≥0，由二项展开式可得整数M1、M2，使得（4﹣1）2s+2=4M1+1，2×（4﹣1）s=8M2+（﹣1）S2∴4m=4（M1﹣2M2）﹣（（﹣1）S+1）2，∴存在整数m满足要求．故当且仅当p=3s，s∈N，命题成立．【点评】本题考查数列的性质和应用，解题时要认真审题，仔细解答，注意公式的灵活运用．。

上海市2009年高三十校联考模拟考试数学（理科）试卷一. 填空题（本大题满分60分）本大题共有12题，只要求直接填写结果，每个空格填对得5分，否则一律得零分．1. 若()22311n n n C C C n *--=+∈N，则n =_____________． 2. 若复数z 满足132i 2izz =--（i 是虚数单位），则z =__________． 3. 已知1tan 62πα⎛⎫+= ⎪⎝⎭，tan 36πβ⎛⎫-= ⎪⎝⎭，则()tan αβ+=____________． 4. 由0，1，2，3，4，5六个数字组成无重复数字且数字2，3相邻的四位数共_______个（结果用数字表示）．5. 函数44sin cos y x x =+的单调递增区间是______________________．6. 科学家以里氏震级来度量地震的强度，若设I 为地震时所散发出来的相对能量强度，则里氏震级量度r 可定义为2lg 23r I =+．2008年5月12日，四川汶川发生的地震是8.0级，而1976年唐山地震的震级为7.8级，那么汶川地震所散发的相对能量是唐山地震所散发的相对能量的_____________倍．（精确到个位）7. 在一个水平放置的底面半径为3cm 的圆柱形量杯中装有适量的水，现放入一个半径为R cm 的实心铁球，球完全浸没于水中且无水溢出，若水面高度恰好上升R cm ，则R =________cm ．8. 已知平面上直线l 的方向向量()3,4d →=-，点()0,0O 和()4,2A -在l 上的射影分别是1O 和1A ，则11O A =________________．9. 已知函数()f x =的值域是[0,)+∞，则实数m 的取值范围是________________．10. 有一道解三角形的问题，缺少一个条件．具体如下：“在ABC ∆中，已知a =45B =，____________，求角A 的大小．”经推断缺少的条件为三角形一边的长度，且答案提示60A =，试将所缺的条件补充完整．11. 如图，设A 是棱长为a 的正方体的一个顶点，过从此顶点出发的三条棱的中点作截面，对正方体的所有顶点都如此操作，所得的各截面与正方体各面共同围成一个多面体，则关于此多面体有以下结论：①有12个顶点；②有24条棱；③有12个面；④表面积为23a ；⑤体积为365a ．其中正确的结论是____________．（要求填上所有正确结论的序号）12. 在解决问题：“证明数集{}23A x x =<≤没有最小数”时，可用反证法证明．假设()23a a <≤是A 中的最小数，则取22a a +'=，可得：22223222a a aa a +++'=<=<=≤，与假设中“a 是A 中的最小数”矛盾！ 那么对于问题：“证明数集,,,n B x x m n n m m *⎧⎫==∈<⎨⎬⎩⎭N 并且没有最大数”，也可以用反证法证明．我们可以假设0n x m =是B 中的最大数，则可以找到x '=____________（用0m ，0n 表示），由此可知x B '∈，x x '>，这与假设矛盾！所以数集B 没有最大数．二．选择题（本大题满分16分）本大题共有4题，每题都给出四个结论，其中有且只有一个结论是正确的，必须把答题纸上相应题序内的正确结论代号涂黑，选对得 4分，否则一律得零分.13. 圆2286160x y x y +-++=与圆2264x y +=的位置关系是 ( )(A) 相交 (B) 相离 (C) 内切 (D) 外切 14. 已知无穷等比数列}{n a 的前n 项和为n S ，各项的和为S ，且()lim 21n n S S →∞-=，则其首项1a 的取值范围是 ( ) (A)()()1,00,1- (B)()()2,11,0--- (C) ()()0,11,2 (D)()()2,00,2-15. 在平面直角坐标系中，横坐标、纵坐标均为整数的点称为整点，如果函数()y f x =的图像上有且仅有()n n ∈*N个整点，则称函数()y f x =为n 阶整点函数．有下列函数：①()sin 2f x x =； ②()3g x x =； ③()13xh x ⎛⎫= ⎪⎝⎭； ④()ln x x φ=，其中是一阶整点函数的个数为 （ ） （A ）1 （B ）2 （C ）3 （D ）416. 已知正方形ABCD 的面积为36，BC 平行于x 轴，顶点A 、B 和C 分别在函数3log a y x =、2log a y x =和log a y x =（其中1a >）的图像上，则实数a 的值为 ( )(D)三．解答题（本大题满分74分）本大题共有5题，解答下列各题必须在答题纸的规定区域（对应的题号）内写出必要的步骤. 17. (本题满分12分)已知函数()221f x x tx =-+，[]2,5x ∈有反函数，且函数()f x 的最大值为8，求实数t 的值.18. (本题满分14分) 本题共有2个小题，第1小题满分6分，第2小题满分8分.如图，已知四棱锥P ABCD -的底面ABCD 是边长为1的正方形，PD ⊥底面ABCD ，且2PD =．（1） 若点E 、F 分别在棱PB 、AD 上，且4PE EB =，4DF FA =，求证：EF ⊥平面PBC ；（2） 若点G 在线段PA 上，且三棱锥G PBC -的体积为14，试求线段PG 的长．19. (本题满分14分) 本题共有2个小题，第1小题满分6分，第2小题满分8分.已知数列{}n a 满足125a =，且对任意n *∈N ，都有11422n n n n a a a a +++=+．（1） 求证：数列1n a ⎧⎫⎨⎬⎩⎭为等差数列； （2） 试问数列{}n a 中任意连续两项的乘积()1k k a a k *+⋅∈N 是否仍是{}n a 中的项？如果是，请指出是数列的第几项；如果不是，请说明理由．20. (本题满分16分)本题共有3个小题，第1小题满分4分，第2小题满分5分，第3小题满分7分.定义区间(),m n ，[],m n ，(],m n ，[),m n 的长度均为n m -，其中n m >．（1） 若关于x 的不等式221230ax x -->，求实数a的值；（2） 已知关于x的不等式2sin cos 0x x x b ++>，[]0,x π∈的解集构成的各区间的长度和超过3π，求实数b 的取值范围； （3） 已知关于x 的不等式组()2271,1log log 32x x tx t ⎧>⎪+⎨⎪++<⎩的解集构成的各区间长度和为6，求实数t 的取值范围．21. (本题满分18分)本题共有3个小题，第1小题满分5分，第2小题满分5分，第3小题满分8分.已知等轴双曲线C 的两个焦点1F 、2F 在直线y x =上，线段12F F 的中点是坐标原点，且双曲线经过点33,2⎛⎫ ⎪⎝⎭．（1） 若已知下列所给的三个方程中有一个是等轴双曲线C 的方程：①22274x y -=；②9xy =；③92xy =．请确定哪个是等轴双曲线C 的方程，并求出此双曲线的实轴长；（2） 现要在等轴双曲线C 上选一处P 建一座码头，向()3,3A 、()9,6B 两地转运货物．经测算，从P 到A 、从P 到B 修建公路的费用都是每单位长度a 万元，则码头应建在何处，才能使修建两条公路的总费用最低？（3） 如图，函数1y x x=+的图像也是双曲线，请尝试研究此双曲线的性质，你能得到哪些结论？（本小题将按所得到的双曲线性质的数量和质量酌情给分）理科答案说明1. 本解答列出试题的一种解法，如果考生的解法与所列解法不同,可参照解答中评分标准的精神进行评分.2. 评阅试卷，应坚持每题评阅到底，不要因为考生的解答中出现错误而中断对该题的评阅. 当考生的解答在某一步出现错误，影响了后继部分，但该步以后的解答未改变这一题的内容和难度时，可视影响程度决定后面部分的给分，这时原则上不应超过后面部分应给分数之半，如果有较严重的概念性错误，就不给分.3. 第17题至第21题中右端所注的分数，表示考生正确做到这一步应得的该题累加分数.4. 给分或扣分均以1分为单位.答案及评分标准一、（第1至12题）每题正确的给5分，否则一律得零分. 1.5. 2.47i 55-. 3. 7-. 4. 60. 5. (),242k k k πππ⎡⎤-∈⎢⎥⎣⎦Z . 6. 2. 7. 32. 8. 4.9.[][)0,19,+∞. 10. c =. 11. ①②⑤12.答案不惟一，0011n m ++，0002n m m +，…….二、（第13至16题）每一题正确的给4分，否则一律得零分.三、（第17至21题）17.【解】 因为函数有反函数，所以在定义域内是一一对应的函数()221f x x tx =-+的对称轴为x t =，所以2t ≤或5t ≥ …… 3分若2t ≤，在区间[]2,5上函数是单调递增的，所以()()max 5251018f x f t ==-+=，解得95t =，符合 …… 7分 若5t ≥，在区间[]2,5上函数是单调递减的，所以()()max 24418f x f t ==-+=，解得34t =-，与5t ≥矛盾，舍去 …… 11分 综上所述，满足题意的实数t 的值为95……12分18.【解】（1）以点D 为坐标原点，DA 为x 轴正方向，DC 为y 轴正方向建立空间直角坐标系． …… 1分 则()0,0,0D ，()1,0,0A ，()1,1,0B ，()0,1,0C ，()0,0,2P ， 因为4PE EB =，4DF FA =，所以4,0,05F ⎛⎫⎪⎝⎭，442,,555E ⎛⎫⎪⎝⎭， …… 3分 则420,,55EF ⎛⎫=-- ⎪⎝⎭，()1,0,0BC =-，()1,1,2PB =--． …… 5分 0EF BC ⋅=，0EF PB ⋅=，即EF 垂直于平面PBC 中两条相交直线，所以EF ⊥平面PBC ． …… 7分（2）()1,0,2PA =-，可设()01PG PA λλ=≤≤，所以向量PG 的坐标为(),0,2λλ-， …… 8分平面PBC 的法向量为420,,55EF ⎛⎫=-- ⎪⎝⎭． 点G 到平面PCE的距离42PG EFd EFλ⋅===．…… 10分 PBC∆中，1BC =，PC =，PB =2PBC S ∆=．…… 12分三棱锥G PBC -的体积11133234PBC V S d λ∆=⋅=⋅==，所以34λ=． …… 13分此时向量PG 的坐标为33,0,42⎛⎫- ⎪⎝⎭，3PG =PG ． …… 14分19.【解】（1）由11422n n n n a a a a +++=+及125a =可知数列{}n a 的每一项都是正的． …… 1分 111242n n n n n n a a a a a a ++++=+，即11223n n n n a a a a ++-=， …… 3分所以11132n n a a +-=， …… 4分 所以数列1n a ⎧⎫⎨⎬⎩⎭是以52为首项，公差为32的等差数列． ……6分（2）由（1）可得数列1n a ⎧⎫⎨⎬⎩⎭的通项公式为1322n n a +=，所以232n a n =+． …… 8分 ()122243231292110k k a a k k k k +⋅=⋅=+++++ 22921622k k =+++22372322k k =++⋅+． …… 10分 因为()2213723122k k k k k k +++=+++， …… 11分当k *∈N 时，()12k k +一定是正整数，所以23722k k ++是正整数． …… 13分所以1k k a a +⋅是数列{}n a 中的项，是第23722k k ++项． …… 14分20.【解】（1）0a =时不合题意； …… 1分0a ≠时，方程221230ax x --=的两根设为1x 、2x ，则126x x a +=，1232x x a=-，由题意知()22121212236664x x x x x x a a=-=+-=+， …… 2分 解得2a =-或3a =（舍）， …… 3分 所以2a =-． …… 4分（2）因为2sin cos x x x b ++)1sin 21cos 2sin 22232x x b x b π⎛⎫=+++=+++ ⎪⎝⎭， …… 5分 设()sin 23f x x π⎛⎫=+⎪⎝⎭，原不等式等价于“()f x b >，[]0,x π∈”，…… 6分 因为函数()f x 的最小正周期为π，[]0,π的长度恰为函数的一个正周期，所以当122b --<时，()2f x b >--，[]0,x π∈的解集构成的各区间的长度和超过3π，即b的取值范围为⎛⎫+∞ ⎪ ⎪⎝⎭． …… 9分 （3）先解不等式711x >+，整理得601x x -+>+，即()()160x x +-< 所以不等式711x >+的解集()1,6A =- …… 10分 设不等式()22log log 32x tx t ++<的解集为B ，不等式组的解集为AB不等式()22log log 32x tx t ++>等价于2030340x tx t tx tx ⎧>⎪+>⎨⎪+-<⎩…… 11分所以()0,B ⊆+∞，()0,6AB ⊆，不等式组的解集的各区间长度和为6，所以不等式组230340tx t tx tx +>⎧⎨+-<⎩，当()0,6x ∈时，恒成立 …… 12分 当()0,6x ∈时，不等式30tx t +>恒成立，得0t > …… 13分 当()0,6x ∈时，不等式2340tx tx +-<恒成立，即243t x x<+恒成立 …… 14分当()0,6x ∈时，243x x +的取值范围为2,27⎛⎫+∞ ⎪⎝⎭，所以实数227t ≤ …… 15分 综上所述，t 的取值范围为20,27⎛⎤⎥⎝⎦…… 16分21.【解】（1）双曲线22274x y -=的焦点在x 轴上，所以①不是双曲线C 的方程……1分 双曲线9xy =不经过点33,2⎛⎫ ⎪⎝⎭，所以②不是双曲线C 的方程 …… 2分所以③92xy =是等轴双曲线C 的方程 …… 3分 等轴双曲线92xy =的焦点1F 、2F 在直线y x =上，所以双曲线的顶点也在直线y x =上， …… 4分联立方程92xy y x ⎧=⎪⎨⎪=⎩，解得双曲线92xy =的两顶点坐标为22⎛⎫ ⎪ ⎪⎝⎭，,22⎛⎫-- ⎪ ⎪⎝⎭，所以双曲线92xy =的实轴长为6 …… 5分 （2） 所求问题即为：在双曲线92xy =求一点P ，使PA PB +最小．首先，点P 应该选择在等轴双曲线的92xy =中第一象限的那一支上 …… 6分等轴双曲线的92xy =的长轴长为6，所以其焦距为又因为双曲线的两个焦点1F 、2F 在直线y x =上，线段12F F 的中点是原点，所以()3,3A 是92xy =的一个焦点， …… 7分 设双曲线的另一个焦点为()23,3F --，由双曲线的定义知：26PA PF =- 所以()26PA PB PF PB +=-+，要求PA PB +的最小值，只需求2PF PB +的最小值 …… 8分直线2BF 的方程为3430x y --=，所以直线2BF 与双曲线92xy =在第一象限的交点为33,2⎛⎫ ⎪⎝⎭…… 9分所以码头应在建点P 33,2⎛⎫ ⎪⎝⎭处，才能使修建两条公路的总费用最低 …… 10分（3）① ())()1133f x x x f x x x ⎛⎫-=-+=-+=- ⎪ ⎪-⎝⎭，此双曲线是中心对称图形，对称中心是原点()00，；…… 1分② 渐近线是3y x =和0x =．当0x >时，当x 无限增大时，1x无限趋近于0，13y x x =+与3y x =无限趋近；当y 无限增大时，x 无限趋近于0． …… 2分③ 双曲线的对称轴是y =和y x =． …… 3分④ 双曲线的顶点为，⎛⎝，实轴在直线y =上，实轴长为…… 4分⑤虚轴在直线y x =，虚轴长为 …… 5分⑥焦点坐标为，⎛ ⎝，焦距…… 6分 说明：（i ）若考生能把上述六条双曲线的性质都写出，建议此小题给满分8分（ii ）若考生未能写全上述六条双曲线的性质，但是给出了13y x x=+的一些函数性质（诸如单调性、最值），那么这些函数性质部分最多给1分。

2009年高考模拟试卷数学（理科）考试时间120分钟 满分150分本试题卷分第Ⅰ卷和第Ⅱ卷两部分。

全卷共4页，第Ⅰ卷1至2页，第Ⅱ卷3至4页。

满分150分，考试时间120分钟。

请考生按规定用笔将所有试题的答案涂、写在答题纸上。

第Ⅰ卷（共50分）注意事项：1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸上。

2．每小题选出答案后，用2B 铅笔把答题纸上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

不能答在试题卷上。

参考公式：如果事件A 、B 互斥，那么P （A+B ）=P （A ）+（B ）如果事件A 、B 相互独立，那么P （A ·B ）=P （A ）·（B ） 如果事件A 在一次试验中发生的概率是p 那么n 次独立重复试验中恰好发生k 次的概率： k n kk n n p p C k P --=)1()( 球的表面积公式S=42R π （其中R 表示球的半径）求的体积公式334R V π=（其中R 表示球的半径）一、选择题：本大题共10个小题；每小题5分，共50分．在每小题给出的四个选项中，有且只有一项是符合题目要求的．1．如果复数(1—ai)i (a ∈R)的实部与虚部是互为相反数，则a 的值等于（ ） 【原创】 A ．－1 B ．1 C ．－2 D ．2 2．右图是一个几何体的三视图，根据 图中数据，可得该几何体的表面积是 （ ）【原创】A ．32πB ．16πC ．12πD ．8π3．若函数f (x)=log a (x+b)的大致图像如右图，其中a ，b 为常数，则函数g(x)=a x +b 的大致图像是（ ）4．已知l ,m 为两条直线，则下列条件中可以判断平面βα与平面平行的是（ ）【原创】左视图正(主)视俯视图 BA ．βα//,//l lB ．βα⊥⊥l l ,C ．βα//,l l ⊂D ．ββα//,//,,m l m l ⊂5．设平面区域D 是双曲线22x y 14-=的两条渐进线和椭圆22x y 12+=的右准线所围成的三角形含边界及内部，若点(x ，y) ∈D ，则目标函数z= x+y 的最小值为（ ）【深圳市一模改编】A ．1B ．2C ．3D ．6 6．定义行列式运算：12142334a a ||a a a a a a =-，将函数f(x)=cos x||1sin x的图像向左平 移m 个单位(m>o)，若所得对应的函数为偶函数，则m 的最小值为（ ）【根据试题研究改编】A ．23π B ．3π C ．8π D ．56π 7．在右图的表格中，如果每格填上一个数后，每一横行成等差数列，每一纵行成等比数列， 那么x+y+z 的值为（ ）【原创】A ．4B ．3C ． 2D ．18．设m 、n 都是不大于6的自然数，则方程12626=-y C x C n m 表示双曲线的个数是（ ）【原创】 A ．49 B ．36 C ．25 D9．下图给出的是计算1001614121++++ 的值的一个程序框图， 其中判断框内应填入的条件是（ ）【根据课本习题改编】（A ）.i>100 （B ）i<＝100 （C ）i>50 （D ）i<＝5010．一机器狗每秒钟前进或后退一步，程序设计师让机器狗以前进3步，再后退2步的规律移动，如果将此机器狗放在数轴的原点，面向正方向，以一步的距离为一个单位长，令P (n )表示第n 秒时机器狗所在位置的坐标，且P (0)=0，那么下列结论中错误的是（ ）【杭州高中2007第5次模拟试题】 A ． P (3)=3 B ． P (5)=1 C ． P (101)=21 D ． P (103)<P (104)第9题第Ⅱ卷（共100分）注意事项：1．黑色字迹的签字笔或钢笔填写在答题纸上，不能答在试题卷上。

上海市2009年高三十四校联考模拟试卷数学试题（理科）考试用时120分钟 满分150分一、填空题（本大题满分60分，共12小题，每小题满分5分）1．不等式021≥+-x x 的解集为 .2．设θθθ2,54cos ,53sin 则-==的终边所在的象限是.3．以原点为顶点，x 轴为对称轴且焦点在0342=+-y x 上的抛物线方程是 .4．二项式()15153yx -展开式中所有的理系数之和为 .5．设65432,2321z z z z z z i z ++++++=那么= .6．设l 为平面上过点（0，1）的直线，l 的斜率等可能地取ξ且,22,3,25,0,25,3,22--- 表示坐标原点到l 的距离，则随机变量ξ的数学期望E ξ=.7．若数列}{),,(}{*221n nn n a N n p p a a a 则称为正常数满足∈=+为“等方比数列”。

则“数列}{n a 是等方比数列”是“数列}{n a 是等方比数列”的条件.8．一个圆锥的侧面展开图是圆心角为π34，半径为18cm 的扇形，则圆锥母线与底面所成角的余弦值为.9．已知R x f 是定义在)(上的函数，且R x f ∈=对任意的,1)1(都有下列两式成立：)6(,1)()(.1)()1(;5)()5(g x x f x g x f x f x f x f 则若-+=+≤++≥+的值为.10．如图，在杨辉三角中，斜线上方的数组成数列： 1，3，6，10，…，记这个数列的前n 项和为S n ，则nn S n 3lim ∞→=.11．符号][x 表示不超过x 的最大整数，如[2.3]=2，][}{,2]3.1[x x x +=-=-定义函数，那么下列命题中所有正确命题的序号为 .①函数}{x 的定义域是R ；②函数}{x 的值域为R ；③方程23}{=x 有唯一解；④函数}{x 是周期函数；⑤函数}{x 是增函数.12．矩阵的一种运算,⎪⎪⎭⎫⎝⎛++=⎪⎪⎭⎫ ⎝⎛⋅⎪⎪⎭⎫⎝⎛dy cx by ax y x d c b a 该运算的几何意义为平面上的点),(y x 在矩阵⎪⎪⎭⎫⎝⎛d c b a 的作用下变换成点124),,(22=++++y xy x dy cx by ax 若曲线在矩阵⎪⎪⎭⎫ ⎝⎛11b a 的作用下变换成曲线b a y x +=-则,1222的值为 .二、选择题（本大题满分16分，共4小题，每小题满分4分）13．无穷等比数列,42,21,22,1…各项的和等于（）A ．22-B ．22+C ．12+D ．12-14．已知非零向量,21||||,0||||==⋅+AC AB AC AB 满足则△ABC 的形状是（ ）A ．三边均不相等的三角形B ．直角三角形C ．等腰（非等边）三角形D ．等边三角形15．对任意正整数n ，定义n 的双阶乘n ！！如下：当n 为偶数时， 135)4)(2(!!,;246)4)(2(!!⨯⨯--=⨯⨯--= n n n n n n n n n 为奇数时当；现有四个命题：①!2009)!!2008)(!!2009(=，②!10042!!2008⨯=，③2008！！个位数为0，④2009！！个位数为5。