2015届高考理科数学第一轮知识点复习方案测试题55.doc

沁园春·雪<毛泽东>北国风光，千里冰封，万里雪飘。

望长城内外，惟余莽莽；大河上下，顿失滔滔。

山舞银蛇，原驰蜡象，欲与天公试比高。

沁园春·雪 <毛泽东> 北国风光，千里冰封，万里雪飘。

望长城内外，惟余莽莽；大河上下，顿失滔滔。

山舞银蛇，原驰蜡象，欲与天公试比高。

须晴日，看红装素裹，分外妖娆。

江山如此多娇，引无数英雄竞折腰。

惜秦皇汉武，略输文采；唐宗宋祖，稍逊风骚。

一代天骄，成吉思汗，只识弯弓射大雕。

俱往矣，数风流人物，还看今朝。

须晴日，看红装素裹，分外妖娆。

江山如此多娇，引无数英雄竞折腰。

惜秦皇汉武，略输文采；唐宗宋祖，稍逊风骚。

一代天骄，成吉思汗，只识弯弓射大雕。

俱往矣，数风流人物，还看今朝。

第8讲函数与方程一、填空题1．若a >2，则函数f (x )＝13x 3－ax 2＋1在(0,2)内零点的个数为________．解析 依题意得f ′(x )＝x 2－2ax ，由a >2可知，f ′(x )在x ∈(0,2)时恒为负，即f (x )在(0,2)内单调递减，又f (0)＝1>0，f (2)＝83－4a ＋1<0，因此f (x )在(0,2)内只有一个零点．答案 12．已知符号函数sgn(x )＝⎩⎨⎧ 1，x >0，0，x ＝0，－1，x <0，则函数f (x )＝sgn(ln x )－ln 2x的零点个数为________． 解析 依题意得，当x ＞1时，ln x ＞0，sgn(ln x )＝1，f (x )＝sgn(ln x )－ln 2x ＝1－ln 2x ，令1－ln 2x ＝0，得x ＝e 或x ＝1e ，结合x ＞1，得x ＝e ；当x ＝1时，ln x ＝0，sgn(ln x )＝0，f (x )＝－ln 2x ，令－ln 2x ＝0，得x ＝1，符合；当0＜x ＜1时，ln x ＜0，sgn(ln x )＝－1，f (x )＝－1－ln 2x .令－1－ln 2x ＝0，得ln 2x ＝－1，此时无解．因此，函数f (x )＝sg n(ln x )－ln 2x 的零点个数为2.答案 23．若定义在R 上的函数f (x )满足f (x ＋2)＝f (x )，且x ∈[－1,1]时，f (x )＝1－x 2，函数g (x )＝⎩⎪⎨⎪⎧ lg x ，x >0，0，x ＝0，－1x ，x <0，则函数h (x )＝f (x )－g (x )在区间[－5,5]内的零点的个数是________．解析 依题意得，函数f (x )是以2为周期的函数，在同一坐标系下画出函数y ＝f (x )与函数y ＝g (x )的图象，结合图象得，当x ∈[－5,5]时，它们的图象的公共点共有8个，即函数h (x )＝f (x )－g (x )在区间[－5,5]内的零点的个数是8.答案 84．设函数f (x )＝13x －ln x (x ＞0)，则函数f (x )在区间(0,1)，(1，＋∞)内的零点个数分别为________．解析 设y ＝13x 与y ＝ln x ，作图象可知f (x )在区间(0,1)内无零点，在(1，＋∞)内仅有两个零点．答案 0,25．设函数f (x )＝⎩⎨⎧ 4x －4，x ≤1，x 2－4x ＋3，x ＞1，则函数g (x )＝f (x )－log 4x 的零点个数为________．解析 设y ＝f (x )与y ＝log 4x ，分别画出它们的图象，得有2个交点，所以函数g (x )的零点个数为2.答案 26．已知函数f (x )＝⎩⎨⎧2x －1，x ＞0，－x 2－2x ，x ≤0.若函数g (x )＝f (x )－m 有3个零点，则实数m 的取值范围是________．解析 画出图象，令g (x )＝f (x )－m ＝0，即y ＝f (x )与y ＝m 的图象的交点有3个，∴0＜m ＜1.答案 (0,1)7．方程log 2(x ＋4)＝2x 的根有________个．解析 作函数y ＝log 2(x ＋4)，y ＝2x 的图象如图所示，两图象有两个交点，且交点横坐标一正一负，∴方程有一正根和一负根．答案 28．已知函数f (x )＝x 2＋(1－k )x －k 的一个零点在(2,3)内，则实数k 的取值范围是________．解析 因为Δ＝(1－k )2＋4k ＝(1＋k )2≥0对一切k ∈R 恒成立，又k ＝－1时，f (x )的零点x ＝－1∉(2,3)，故要使函数f (x )＝x 2＋(1－k )x －k 的一个零点在(2,3)内，则必有f (2)·f (3)<0，即2<k <3.答案 (2,3)9．若关于x 的方程kx ＋1＝ln x 有解，则实数k 的取值范围是________．解析 如图，若y ＝kx ＋1与y ＝ln x 相切于点P (x 0，y 0)，则⎩⎨⎧ k ＝1x 0，kx 0＋1＝ln x 0，解得x 0＝e 2，k ＝1e 2.欲使方程有解，则y ＝kx ＋1与y ＝ln x 有公共点，所以k ≤1e 2.答案 ⎝ ⎛⎦⎥⎤－∞，1e 2 10．已知函数f (x )＝1＋x －x 22＋x 33－x 44＋…＋x 2 0112 011，g (x )＝1－x ＋x 22－x 33＋x 44－…－x 2 0112 011，设F (x )＝f (x ＋3)·g (x －3)，且函数F (x )的零点均在区间[a ，b ](a ＜b ，a ，b ∈Z )内，则b －a 的最小值为________．解析 由f ′(x )＝1－x ＋x 2－x 3＋…＋x 2 010＝1＋x 2 0111＋x， 则f ′(x )＞0，f (x )为增函数，又f (0)＝1＞0，f (－1)＜0，从而f (x )的零点在(－1,0)上；同理g (x )为减函数，零点在(1,2)上，∴F (x )的零点在(－4，－3)和(4,5)上，要使区间[a ，b ]包含上述区间，则需(b －a )min ＝9. 答案 9二、解答题11．已知函数f (x )＝－x 2＋2e x ＋m －1，g (x )＝x ＋e 2x (x >0)． (1)若g (x )＝m 有零点，求m 的取值范围；(2)试确定m 的取值范围，使得g (x )－f (x )＝0有两个相异实根．解 (1)∵g (x )＝x ＋e 2x ≥2e 2＝2e ，等号成立的条件是x ＝e ，故g (x )的值域是[2e ，＋∞)，因而只需m ≥2e ，则g (x )＝m 就有零点．(2)若g (x )－f (x )＝0有两个相异的实根，即g (x )与f (x )的图象有两个不同的交点．作出g (x )＝x ＋e 2x (x >0)和f (x )的图象如图．∵f (x )＝－x 2＋2e x ＋m －1＝－(x －e)2＋m －1＋e 2，其对称轴为直线x ＝e ，开口向下，最大值为m －1＋e 2，故当m －1＋e 2>2e ，即m >－e 2＋2e ＋1时，g (x )与f (x )有两个交点，即g (x )－f (x )＝0有两个相异实根，∴m 的取值范围是m >－e 2＋2e ＋1.12．已知二次函数f (x )＝4x 2－2(p －2)x －2p 2－p ＋1在区间[－1,1]内至少存在一个实数c ，使f (c )＞0，求实数p 的取值范围．解 二次函数f (x )在区间[－1,1]内至少存在一个实数c ，使f (c )＞0的否定是对于区间[－1,1]内的任意一个x 都有f (x )≤0，∴⎩⎪⎨⎪⎧ f (1)≤0，f (－1)≤0，即⎩⎪⎨⎪⎧ 4－2(p －2)－2p 2－p ＋1≤0，4＋2(p －2)－2p 2－p ＋1≤0，整理得⎩⎪⎨⎪⎧2p 2＋3p －9≥0，2p 2－p －1≥0， 解得p ≥32或p ≤－3，∴二次函数f (x )在区间[－1,1]内至少存在一个实数c ，使f (c )＞0的实数p 的取值范围是⎝ ⎛⎭⎪⎫－3，32. 13．已知函数f (x )＝|x －a |－a 2ln x ，a ∈R .(1)求函数f (x )的单调区间；(2)若函数f (x )有两个零点x 1，x 2(x 1<x 2)，求证：1<x 1<a <x 2<a 2.(1)解 由题意，函数的定义域为(0，＋∞)，当a ≤0时，f (x )＝|x －a |－a 2ln x ＝x －a －a 2ln x ，f ′(x )＝1－a 2x >0，函数f (x )的单调递增区间为(0，＋∞)．当a >0时，f (x )＝|x －a |－a 2ln x ＝⎩⎪⎨⎪⎧ x －a －a 2ln x ，x ≥a ，a －x －a 2ln x ，0<x <a ，若x ≥a ，f ′(x )＝1－a 2x ＝2x －a 2x >0，此时函数f (x )单调递增，若0<x<a，f′(x)＝－1－a2x<0，此时函数f(x)单调递减，综上，当a≤0时，函数f(x)的单调递增区间为(0，＋∞)；当a>0时，函数f(x)的单调递减区间为(0，a)；单调递增区间为(a，＋∞)．(2)证明由(1)知，当a≤0时，函数f(x)单调递增，至多只有一个零点，不合题意；则必有a>0，此时函数f(x)的单调递减区间为(0，a)；单调递增区间为(a，＋∞)，由题意，必须f(a)＝－a2ln a<0，解得a>1.由f(1)＝a－1－a2ln 1＝a－1>0，f(a)<0，得x1∈(1，a)．而f(a2)＝a2－a－a ln a＝a(a－1－ln a)，下面证明：a>1时，a－1－ln a>0.设g(x)＝x－1－ln x，x>1，则g′(x)＝1－1x＝x－1x>0，∴g(x)在x>1时递增，则g(x)>g(1)＝0，∴f(a2)＝a2－a－a ln a＝a(a－1－ln a)>0，又f(a)<0，∴x2∈(a，a2)，综上，1<x1<a<x2<a2.14．设函数f(x)＝3ax2－2(a＋c)x＋c (a>0，a，c∈R)．(1)设a>c>0.若f(x)>c2－2c＋a对x∈[1，＋∞)恒成立，求c的取值范围；(2)函数f(x)在区间(0,1)内是否有零点，有几个零点？为什么？解(1)因为二次函数f(x)＝3ax2－2(a＋c)x＋c的图象的对称轴为x＝a＋c 3a，由条件a>c>0，得2a>a＋c，故a＋c3a<2a3a＝23<1，即二次函数f(x)的对称轴在区间[1，＋∞)的左边，且抛物线开口向上，故f(x)在[1，＋∞)内是增函数．若f(x)>c2－2c＋a对x∈[1，＋∞)恒成立，则f(x)min＝f(1)>c2－2c＋a，即a －c >c 2－2c ＋a ，得c 2－c <0，所以0<c <1.(2)①若f (0)·f (1)＝c ·(a －c )<0，则c <0，或a <c ，二次函数f (x )在(0,1)内只有一个零点． ②若f (0)＝c >0，f (1)＝a －c >0，则a >c >0.因为二次函数f (x )＝3ax 2－2(a ＋c )x ＋c 的图象的对称轴是x ＝a ＋c 3a .而f ⎝ ⎛⎭⎪⎫a ＋c 3a ＝－a 2＋c 2－ac 3a<0， 所以函数f (x )在区间⎝ ⎛⎭⎪⎫0，a ＋c 3a 和⎝ ⎛⎭⎪⎫a ＋c 3a ，1内各有一个零点，故函数f (x )在区间(0,1)内有两个零点．希望的灯一旦熄灭，生活刹那间变成了一片黑暗。

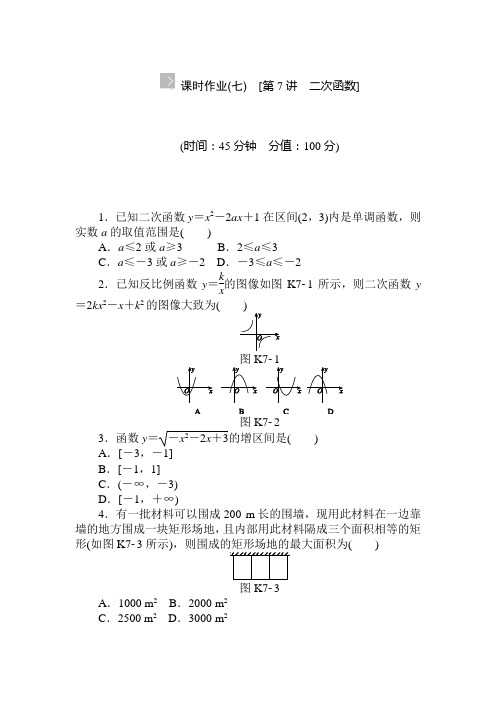
课时作业(七) [第7讲 二次函数](时间：45分钟 分值：100分)1．已知二次函数y ＝x 2－2ax ＋1在区间(2，3)内是单调函数，则实数a 的取值范围是( )A ．a ≤2或a ≥3B ．2≤a ≤3C ．a ≤－3或a ≥－2D ．－3≤a ≤－22．已知反比例函数y ＝k x 的图像如图K7­1所示，则二次函数y＝2kx 2－x ＋k 2的图像大致为( )图K7­1K7­3．函数y ＝－x 2－2x ＋3的增区间是( )A ．[－3，－1]B ．[－1，1]C ．(－∞，－3)D ．[－1，＋∞)4．有一批材料可以围成200 m 长的围墙，现用此材料在一边靠墙的地方围成一块矩形场地，且内部用此材料隔成三个面积相等的矩形(如图K7­3所示)，则围成的矩形场地的最大面积为( )图K7­3A ．1000 m 2B ．2000 m 2C ．2500 m 2D ．3000 m 25．[2013·惠州模拟] 生产一定数量商品的全部费用称为生产成本，某企业一个月生产某种商品x 万件时的生产成本为C (x )＝12x 2＋2x ＋20(万元)，一万件的售价是20万元，为获取最大利润，该企业一个月应生产该商品的数量为( )A ．36万件B ．18万件C ．22万件D ．9万件6．某汽车运输公司购买了一批新型大客车投入营运，据市场分析，每辆客车营运的总利润y (10万元)与营运年数x (x ∈N *)满足二次函数关系，其图像如图K7­4所示，为了使营运的年平均利润最大，则每辆客车应营运( )图K7­4A ．6年B ．7年C ．8年D ．9年 7．已知函数f (x )＝⎩⎪⎨⎪⎧x 2＋4x ，x ≥0，4x －x 2，x <0.若f (2－a 2)>f (a )，则实数a 的取值范围是( )A ．(－∞，－1)∪(2，＋∞)B ．(－1，2)C ．(－2，1)D ．(－∞，－2)∪(1，＋∞)8．[2013·枣庄模拟] 已知函数f (x )＝x 2＋1的定义域为[a ，b ](a <b )，值域为[1，5]，则在平面直角坐标系内，点(a ，b )的运动轨迹与两坐标轴所围成的图形的面积是( )A ．8B ．6C ．4D ．29．设函数f (x )＝ax 2＋bx ＋c (a <0)的定义域为D .若所有点(s ，f (t ))(s ，t ∈D )构成一个正方形区域，则a 的值为( )A ．－2B ．－4C ．－8D ．不能确定10．若二次函数的图像过点(4，－3)，且x ＝3时，二次函数有最大值－1，则此函数的解析式为________．11．[2013·天津重点中学联考] 已知函数y ＝x 2＋ax －1＋2a 的值域为[0，＋∞)，则a 的取值范围是________．12．[2013·蚌埠一检] 数列{a n }是首项a 1＝m ，公差d ＝2的等差数列，数列{b n }满足2b n ＝(n ＋1)a n .若对任意n ∈N *都有b n ≥b 5成立，则m 的取值范围是________．13．[2013·金丽衢十二校一联] 设f (x )是定义在R 上的偶函数，且当x ≥0时，f (x )＝2x .若对任意的x ∈[a ，a ＋2]，不等式f (x ＋a )≥f 2(x )恒成立，则实数a 的取值范围是________．14．(10分)某企业投资100万元引进一条农产品加工生产线，若不计维修、保养费用，预计投产后每年可创利33万元．该生产线投产后，从第1年到第x 年的维修、保养费用累计为y (万元)，且y ＝ax 2＋bx .若第1年的维修、保养费为2万元，第2年为4万元．(1)求y 的函数关系式；(2)投产后，这个企业在第几年就能收回投资？15．(13分)已知f (x )＝ax 2＋(2a －1)x －3在⎣⎢⎡⎦⎥⎤－32，2上的最大值为1，求实数a 的值．16．(12分)已知函数f (x )＝ax 2＋bx ＋1(a ，b 为实数)，x ∈R ，F (x )＝⎩⎪⎨⎪⎧f （x ）（x >0），－f （x ）（x <0）.(1)若f (－1)＝0，且函数f (x )的值域为[0，＋∞)，求F (x )的表达式；(2)在(1)的条件下，当x ∈[－2，2]时，g (x )＝f (x )－kx 是单调函数，求实数k 的取值范围；(3)设m ·n <0，m ＋n >0，a >0且f (x )为偶函数，判断F (m )＋F (n )能否大于零．课时作业(七)1．A 2.D 3.A 4.C 5.B 6.B 7.C 8.C 9.B10．y ＝－2x 2＋12x －19 11.a ≥4＋2 3或a ≤4－2 312．[－22，－18] 13.⎝ ⎛⎦⎥⎤－∞，－32 14．(1)y ＝x 2＋x (2)第4年 15.a ＝34或a ＝－3＋2 22 16．(1)F (x )＝⎩⎪⎨⎪⎧（x ＋1）2（x >0），－（x ＋1）2（x <0）(2)k ≥6或k ≤－2 (3)能大于零薄雾浓云愁永昼， 瑞脑消金兽。

45分钟滚动基础训练卷(七)(考查范围：第28讲～第32讲 分值：100分)一、选择题(本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．[2013·辽宁卷] 下面是关于公差d >0的等差数列{}a n 的四个命题：p 1：数列{a n }是递增数列；p 2：数列{na n }是递增数列；p 3：数列⎩⎨⎧⎭⎬⎫a n n 是递增数列； p 4：数列{}a n ＋3nd 是递增数列．其中为真命题的是( )A ．p 1，p 2B ．p 3，p 4C ．p 2，p 3D ．p 1，p 42．[2013·马鞍山二模] 在等比数列{a n }中，a 5a 3＝4，则S 4S 2等于( )A ．5B ．－3C ．±5D ．33．[2013·福建莆田一检] 已知S n 是等差数列{a n }的前n 项和，且S 5<S 6＝S 7>S 8，则下列结论错误的是( )A ．公差d <0B ．a 7＝0C ．S 9>S 5D ．S 6，S 7均为S n 最大值4．[2013·北京海淀区二模] 已知数列{a n }是公比为q 的等比数列，且a 1·a 3＝4，a 4＝8，则a 1＋q 的值为( )A ．3B ．2C ．3或－2D ．3或－35．[2013·河南商丘三模] 若S n 是等差数列{a n }的前n 项和，且S 8－S 4＝12，则S 12的值为( )A ．64B ．44C ．36D ．226．[2013·福州质检] 已知等比数列{a n }的公比q ＝2，且2a 4，a 6，48成等差数列，则数列{a n }的前8项的和为( )A ．127B ．255C ．511D ．10237．[2013·安徽池州质检] 已知－9，a 1，a 2，a 3，－1五个实数成等差数列，－9，b 1，b 2，b 3，－1五个实数成等比数列，则a 1－a 3b 2等于( )A.43 B ．－43C ．±43D ．±238．[2013·西安三模] 若数列{a n }满足a 1＝15，且3a n ＋1＝3a n －2，则使a k a k ＋1<0的k 的值为( )A ．22B ．21C ．24D ．23二、填空题(本大题共3小题，每小题5分，共15分，把答案填在题中横线上)9．[2013·汕头一模] 已知数列{a n }为12，－2，92，－8，252，－18，…，用观察法写出满足数列{a n }的一个通项公式a n ＝________.10．[2013·北京西城区二模] 在等差数列{a n }中，a 2＝5，a 1＋a 4＝12，则a n ＝________；设b n ＝1a 2n －1(n ∈N *)，则数列{b n }的前n 项和S n ＝________．11．[2013·河南十校三联] 设数列{a n }是等差数列，数列{b n }是等比数列，记{a n }，{b n }的前n 项和分别为S n ，T n .若a 3＝b 3，a 4＝b 4，且S 5－S 3T 4－T 2＝5，则a 5＋a 3b 5＋b 3＝________. 三、解答题(本大题共3小题，每小题15分，共45分，解答应写出文字说明，证明过程或演算步骤)12．[2013·陕西卷] 设S n 表示数列{a n }的前n 项和．(1)若{a n }是等差数列，推导S n 的计算公式；(2)若a 1＝1，q ≠0，且对所有正整数n ，有S n ＝1－q n1－q.判断{a n }是否为等比数列，并证明你的结论．13．[2013·天津重点中学联考] 设等比数列{a n }的前n 项和为S n ，已知a n ＋1＝2S n ＋2(n ∈N *)．(1)求数列{a n }的通项公式；(2)在a n 与a n ＋1之间插入n 个数，使这n ＋2个数组成公差为d n的等差数列．设数列⎩⎨⎧⎭⎬⎫1d n 的前n 项和为T n ，证明：T n <1516.14．[2013·开封四模] 已知公差不为0的等差数列{a n }的首项a 1＝2，且1a 1，1a 2，1a 4成等比数列． (1)求数列{a n }的通项公式；(2)若数列{b n }满足b 1＋2b 2＋22b 3＋…＋2n -1b n ＝a n ，求数列{nb n }的前n 项和T n .45分钟滚动基础训练卷(七)1．D 2.A 3.C 4.D 5.C 6.B 7.A 8.D9．(－1)n -1·n 22或(－1)n +1·n 22(本题答案有多种可能)10．2n ＋1 n 4（n ＋1）11．－3512．(1)S n ＝n （a 1＋a n ）2(2){a n }是首项为1，公比为q 的等比数列，证明略13．(1)a n ＝2·3n -1 (2)略14．(1)a n ＝2n (2)T n ＝8－n ＋22n －2。

课时作业(二十七) [第27讲 平面向量的数量积与平面向量应用举例](时间：45分钟 分值：100分)1．[2013·宁波二模] 设a ，b 为两个非零向量，则“a·b ＝|a|·|b|”是“a 与b 共线”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件2．[2013·福建卷] 在四边形ABCD 中，AC →＝(1，2)，BD →＝(－4，2)，则该四边形的面积为( )A. 5 B ．2 5 C ．5 D ．103．[2013·杭州一检] 平面向量a 与b 的夹角为60°，且a ＝(2，0)，|b |＝1，则|a ＋2b |＝( )A. 3 B ．2 3 C ．4 D ．124．[2013·山东卷] 在平面直角坐标系xOy 中，已知OA →＝(－1，t )，OB→＝(2，2)．若∠ABO ＝90°，则实数t 的值为________． 5．[2013·山东济宁一模] 在△ABC 中，G 是△ABC 的重心，AB ，AC 的边长分别为2，1，∠BAC ＝60°，则AG→·BG →＝( ) A ．－89 B ．－109 C ．5－39 D ．－5－396．[2013·湖北卷] 已知点A (－1，1)，B (1，2)，C (－2，－1)，D (3，4)，则向量AB→在CD →方向上的投影为( ) A ．3 22 B ．3 152 C ．－3 22 D ．－3 1527．[2013·唐山一模] 已知向量a ，b 满足(a ＋2b )·(a －b )＝－6，且|a|＝1，|b |＝2，则a 与b 的夹角为( )A.π6B.π3C.2π3D.5π68．[2013·烟台一模] 在△ABC 中，AB ＝3，AC ＝2，BD →＝12BC →，则AD→·BD →的值为( ) A ．－52 B ．52 C ．－54 D ．549．[2013·洛阳统考] 直角三角形ABC 中，∠C ＝90°，BC ＝2，AD→＝tAB →，其中1≤t ≤3，则BC →·DC →的最大值为( ) A ．12 B ．2 2 C ．3 D ．8 210．[2013·北京海淀区模拟] 若向量a ，b 满足|a |＝|b |＝|a ＋b |＝1，则a·b 的值为________．11．[2013·龙岩一检] 已知向量m ＝(1，cos α－12)，n ＝(sin α，1)，且m ⊥n ，则sin 2α等于________．12．[2013·淮安调研] 若平面向量α，β满足|α|＝1，|β|≤1，且以向量α，β为邻边的平行四边形的面积为12，则α与β的夹角θ的取值范围是________．13．[2013·石家庄二检] 在矩形ABCD 中，AB ＝2，BC ＝1，E 为BC 的中点，若F 为该矩形内(含边界)任意一点，则AE →·AF →的最大值为________．14．(10分)设在平面上有两个向量a ＝(cos 2α，sin 2α)(0≤α<π)，b ＝(12，32)，a 与b 不共线．(1)求证：向量a ＋b 与a －b 垂直；(2)当向量3a ＋b 与a －3b 的模相等时，求α的大小．15．(13分)如图K27­1所示，已知在等边三角形ABC 中，点P 为线段AB 上一点，且AP→＝λAB →(0≤λ≤1)． (1)若等边三角形ABC 的边长为6，且λ＝13，求|CP →|； (2)若CP →·AB →≥P A →·PB→，求实数λ的取值范围．图K27­116．(12分)[2013·安庆三模] 如图K27­2所示，倾斜角为θ的直线OP 与单位圆在第一象限的部分交于点P ，单位圆与坐标轴交于点A (－1，0)，点B (0，－1)，P A 与y 轴交于点N ，PB 与x 轴交于点M ，设PO→＝xPM →＋yPN →(x ，y ∈R )． (1)用角θ表示点M 、点N 的坐标； (2)求x ＋y 的最小值．图K27­2课时作业(二十七)1．A 2.C 3.B 4.5 5.A 6.A 7.B 8.C 9.A10．－12 11.－34 12.⎣⎢⎡⎦⎥⎤π6，5π6 13.9214．(1)略 (2)α＝5π12或α＝11π12 15.(1)27 (2)⎣⎢⎡⎦⎥⎤2－22，1 16．(1)N (0，sin θ1＋cos θ)，M (cos θ1＋sin θ，0) (2)2薄雾浓云愁永昼， 瑞脑消金兽。

课时作业(五) [第5讲 函数的单调性与最值](时间：45分钟 分值：100分)1．下列函数f (x )中，满足“对任意x 1，x 2∈(0，＋∞)，当x 1<x 2时，都有f (x 1)>f (x 2)的是( )A ．f (x )＝1xB ．f (x )＝(x －1)2C ．f (x )＝e xD ．f (x )＝ln(x ＋1)2．已知函数f (x )＝ax 2－2ax ＋3－b (a >0)在[1，3]上有最大值5和最小值2，则a ＋b ＝( )A ．0B ．1C ．－1D ．23．已知f (x )为R 上的减函数，则满足f (1x )>f (1)的实数x 的取值范围是( )A ．(－∞，1)B ．(1，＋∞)C ．(－∞，0)∪(0，1)D ．(－∞，0)∪(1，＋∞)4．已知函数f (x )＝－x 2＋ax －b ＋1(a ，b ∈R )对任意实数x 都有f (1－x )＝f (1＋x )成立．若当x ∈[－1，1]时，f (x )>0恒成立，则实数b 的取值范围是( )A ．－1<b <0B ．b <－2C ．b <－1或b >2D ．不能确定5．函数y ＝x ＋1－x －1的值域为( )A ．(－∞，2]B ．(0，2]C ．[2，＋∞)D ．[0，＋∞)6．已知m >2，点(m －1，y 1)，(m ，y 2)，(m ＋1，y 3)都在二次函数y ＝x 2－2x 的图像上，则( )A ．y 1<y 2<y 3B ．y 1<y 3<y 2C ．y 2<y 1<y 3D ．y 3<y 2<y 17．[2013·安庆一中三模] 定义在R 上的函数f (x )＝e x ＋e －x ＋|x |，则满足f (2x －1)<f (3)的x 的取值范围是( )A ．(－2，2)B ．(－∞，2)C ．(2，＋∞)D ．(－1，2)8．[2013·金华模拟] 设函数f (x )＝⎩⎪⎨⎪⎧x 2－6x ＋6，x ≥0，3x ＋4，x <0.若互不相等的实数x 1，x 2，x 3满足f (x 1)＝f (x 2)＝f (x 3)，则x 1＋x 2＋x 3的取值范围是( )A.⎝ ⎛⎦⎥⎤203，263 B. (203，263) C.⎝ ⎛⎦⎥⎤113，6 D. (113，6) 9．设g (x )是定义在R 上以1为周期的函数．若f (x )＝x ＋g (x )在[3，4]上的值域为[－2，5]，则f (x )在区间[－10，10]上的值域为( )A ．[－15，11]B ．[－15，12]C ．[－19，10]D ．[－12，15]10．函数y ＝1－x ＋x ＋3的最大值和最小值分别是________．11．函数f (x )＝x 2－|x |的单调递减区间是________．12．设函数f (x )＝⎩⎪⎨⎪⎧x 2－4x ＋6，x ≥0，x ＋6，x <0，则不等式f (x )>f (1)的解集是________．13．[2013·茂名二模] 若对∀x ∈A ，y ∈B (A ⊆R ，B ⊆R )有唯一确定的f (x ，y )与之对应，则称f (x ，y )为关于x ，y 的二元函数．定义满足下列性质的二元函数f (x ，y )为关于x ，y 的广义“距离”：(1)非负性：f (x ，y )≥0，当且仅当x ＝y 时取等号；(2)对称性：f (x ，y )＝f (y ，x )；(3)三角不等式：f (x ，y )≤f (x ，z )＋f (z ，y )对任意的实数z 均成立． 现给出三个二元函数：①f (x ，y )＝|x －y |；②f (x ，y )＝(x －y )2；③f (x ，y )＝x －y .请选出所有能够成为关于x ，y 的广义“距离”的函数序号：________．14．(10分)函数f (x )＝log 9(x ＋8－a x )在[1，＋∞)上是增函数，求a 的取值范围．15．(13分)利用单调性的定义证明：函数f(x)＝x＋2在[－2，＋∞)上是增函数．16．(12分)已知函数f(x)的定义域是{x|x≠0}，对定义域内的任意x1，x2都有f(x1·x2)＝f(x1)＋f(x2)，且当x>1时f(x)>0，f(2)＝1.(1)求证：f(x)是偶函数；(2)求证：f(x)在(0，＋∞)上是增函数；(3)解不等式f(2x2－1)<2.课时作业(五)1．A 2.B 3.D 4.B 5.B 6.A 7.D 8.D 9.A 10.22，211.⎝ ⎛⎦⎥⎤－∞，－12，⎣⎢⎡⎦⎥⎤0，12 12．(－3，1)∪(3，＋∞) 13.① 14.[－1，9) 15.略16．(1)略 (2)略 (3) (－102，0)∪(0，102)薄雾浓云愁永昼， 瑞脑消金兽。

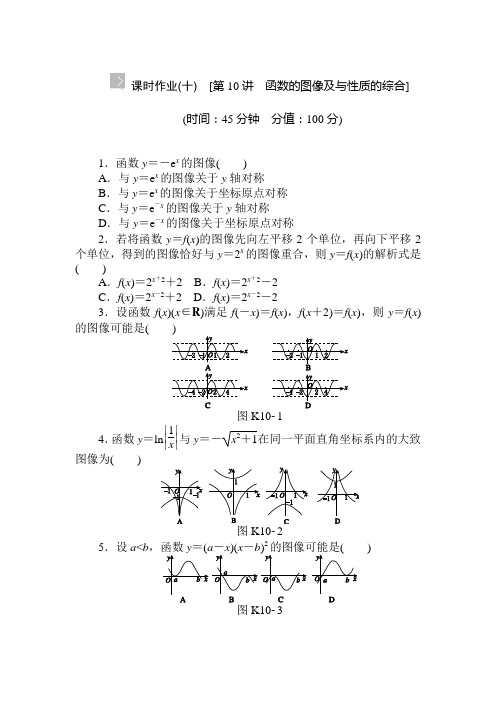
课时作业(十) [第10讲 函数的图像及与性质的综合](时间：45分钟 分值：100分)1．函数y ＝－e x 的图像( ) A ．与y ＝e x 的图像关于y 轴对称 B ．与y ＝e x 的图像关于坐标原点对称 C ．与y ＝e －x 的图像关于y 轴对称D ．与y ＝e －x 的图像关于坐标原点对称2．若将函数y ＝f (x )的图像先向左平移2个单位，再向下平移2个单位，得到的图像恰好与y ＝2x 的图像重合，则y ＝f (x )的解析式是( )A ．f (x )＝2x ＋2＋2B ．f (x )＝2x ＋2－2C ．f (x )＝2x －2＋2D ．f (x )＝2x －2－23．设函数f (x )(x ∈R )满足f (－x )＝f (x )，f (x ＋2)＝f (x )，则y ＝f (x )的图像可能是( )图K10­14．函数y ＝ln ⎪⎪⎪⎪⎪⎪1x 与y ＝－x 2＋1在同一平面直角坐标系内的大致图像为( )图K10­5．设a <b ，函数y ＝(2的图像可能是( )图K10­36．[2013·济南模拟] 函数f (x )＝ln(x －1x )的图像是( )图K10­47．[2013·河南十所名校联考] 已知函数f (x )是定义在R 上的增函数，则函数y ＝f (|x －1|)－1的图像可能是( )图K108．[2013·宁德质检] 已知函数f (x )的图像如图K10­6所示，则f (x )的解析式可以是( )图K10­6A ．f (x )＝ln|x |xB ．f (x )＝e xxC ．f (x )＝1x 2－1D ．f (x )＝x －1x9．[2013·昆明模拟] 函数f (x )＝18x 2＋ln|x |的图像大致是()图K10­710．若函数y ＝f (x ＋3)的图像经过点P (1，4)，则函数y ＝f (x )的图像必经过点________．11．设函数y ＝f (x )定义在实数集上，则函数y ＝f (x －1)与y ＝f (1－x )的图像的对称轴方程是________．12．已知函数f (x )对∀x ∈R 恒满足f (2＋x )＝f (2－x )．若方程f (x )＝0恰有5个不同的实数根，则5个根之和为________．13．[2013·日照模拟] 定义域为R 的函数f (x )满足f (x ＋2)＝2f (x )，当x ∈[0，2)时，f (x )＝[)[)23201,11,2.2-⎧-∈⎪⎪⎨⎛⎫⎪-∈ ⎪⎪⎝⎭⎩x x x x x ，，，若x ∈[－4，－2)时，f (x )≥t 4－12t 恒成立，则实数t 的取值范围是________．14．(10分)(1)已知函数y ＝f (x )的定义域为R ，且当x ∈R 时，f (m ＋x )＝f (m －x )恒成立，求证：y ＝f (x )的图像关于直线x ＝m 对称；(2)若函数f (x )＝log 2|ax －1|的图像的对称轴是x ＝2，求非零实数a 的值．15．(13分)[2013·江西重点中学一联] 定义在R 上的函数f (x )满足f (0)＝0，f (x )＋f (1－x )＝1，f (x 3)＝12f (x )，且当0≤x 1<x 2≤1时，有f (x 1)≤f (x 2)，求f (12013)的值．16．(1)(6分)[2013·新课标全国卷Ⅰ] 已知函数f (x )＝⎩⎪⎨⎪⎧－x 2＋2x ，x ≤0，ln （x ＋1），x ＞0.若|f (x )|≥ax ，则a 的取值范围是( )A ．(－∞，0]B ．(－∞，1]C ．[－2，1]D ．[－2，0](2)(6分)[2013·天津滨海新区重点中学联考] 已知函数f (x )＝⎩⎪⎨⎪⎧1－|x ＋1|，x ∈[－2，0]，2f （x －2），x ∈（0，＋∞）.若方程f (x )＝x ＋a 在区间[－2，4]内有3个不等的实根，则实数a 的取值范围是( )A ．{a |－2<a <0}B ．{a |－2<a ≤0}C ．{a |－2<a <0或1<a <2}D ．{a |－2<a <0或a ＝1}课时作业(十)1．D 2．C 3．B 4．C 5．B 6．B 7．B 8．A 9．C 10．(4，4) 11.x ＝1 12.10 13．(－∞，－2]∪(0，1] 14．(1)略 (2)12 15．1128 16．(1)D (2)D薄雾浓云愁永昼， 瑞脑消金兽。

45分钟滚动基础训练卷(六)(考查范围：第25讲～第27讲 分值：100分)一、选择题(本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．[2013·咸阳二模] “AB→＝DC →”是“四边形ABCD 为平行四边形”的( )A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件2．[2013·北京顺义区一模] 已知向量a ＝(2，1)，b ＝(－2，k )，且a ⊥(2a －b )，则实数k ＝( )A ．－14B ．－6C ．6D ．143．[2013·太原调研] 如图G6-1所示，在矩形OABC 中，点E ，F分别在AB ，BC 上，且满足AB ＝3AE ，BC ＝3CF .若OB→＝λOE →＋μOF →(λ，μ∈R )，则λ＋μ＝( )图G6-1 A.83 B.32 C.53 D ．14．[2013·开封四模] 若|a |＝1，|b |＝2，c ＝a ＋b ，且c ⊥a ，则向量a 与b 的夹角为( )A ．30°B ．60°C ．120°D ．150°5．[2013·呼和浩特模拟] 在△ABC 中，AC →·AB →|AB →|＝1，AB →·BC →|AB →|＝－2，则AB 边的长度为( )A ．1B ．3C ．5D ．96．[2013·烟台模拟] 已知AB→，AC →是非零向量，且满足(AB →－2AC→)⊥AB →，(AC →－2AB →)⊥AC →，则△ABC 的形状是( ) A ．等腰三角形 B ．直角三角形C ．等腰直角三角形D ．等边三角形7．[2013·厦门质检] 如图G6-2所示，在边长为2的菱形ABCD 中，∠ABC ＝60°，对角线相交于点O ，P 是线段BD 的一个三等分点，则AP →·AC→等于( )图G6-2 A ．1 B ．2 C ．3 D ．48．[2013·河南三模] 设向量a ＝(3sin θ＋cos θ＋1，1)，b ＝(1，1)，θ∈⎣⎢⎡⎦⎥⎤π3，2π3，m 是向量a 在向量b 方向上的投影，则m 的最大值是( ) A.3 22 B ．4C ．2 2D ．3二、填空题(本大题共3小题，每小题5分，共15分，把答案填在题中横线上)9．[2013·潮州二模] 已知向量a ＝(1，3)，b ＝(－1，0)，则|a ＋2b |＝________.10．[2013·江西八校联考] 已知向量a ，b 满足|a|＝2，|b |＝1，且(a ＋b )⊥（a －52b ），则a 与b 的夹角为________．11．[2013·上海徐汇区一模] 在△ABC 中，∠A ＝60°，M 是AB的中点．若|AB |＝2，|BC |＝23，D 在线段AC 上运动，则DB →·DM→的最小值为________．三、解答题(本大题共3小题，每小题15分，共45分，解答应写出文字说明，证明过程或演算步骤)12．[2013·黑龙江哈工大附中月考] 如图G6-3所示，在△OAB中，已知P 为线段AB 上的一点，OP→＝xOA →＋yOB →. (1)若BP →＝P A →，求x ，y 的值；(2)若BP →＝3P A →，|OA →|＝4，|OB →|＝2，且OA →与OB →的夹角为60°，求OP →·AB→的值．图G6-313．[2013·福建泉州四校联考] 设平面内的向量OA→＝(－1，－3)，OB →＝(5，3)，OM →＝(2，2)，点P 在直线OM 上，且P A →·PB→＝－16. (1)求OP→的坐标； (2)求∠APB 的余弦值；(3)设t ∈R ，求|OA→＋tOP →|的最小值．14．[2013·太原二模] 已知f (x )＝a·b ，其中a ＝(2cos x ，－3sin 2x )，b ＝(cos x ，1)(x ∈R )．(1)求f (x )的最小正周期和单调递减区间；(2)在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，f (A )＝－1，a ＝7，AB →·AC→＝3，求b 和c 的值(b >c )．45分钟滚动基础训练卷(六)1．B 2.D 3.B 4.C 5.B 6.D 7.B 8.C9．2 10.π3 11.231612．(1)x ＝12，y ＝12(2)OP→·AB →＝－9 13．(1)OP →＝(1，1) (2)cos ∠APB ＝－45 (3) 214．(1)T ＝π f (x )的单调递减区间为⎣⎢⎡⎦⎥⎤k π－π6，k π＋π3，k ∈Z (2)b ＝3，c ＝2薄雾浓云愁永昼， 瑞脑消金兽。

课时作业(八)A [第8讲 指数与对数的运算](时间：30分钟 分值：80分)1．Log 22＝( )A ．－ 2B ． 2C ．－12D ．122.[]（－2）2－1＝( )A. 2 B ．－ 2C.22 D ．－22 3．若log m n ·log 3m ＝2，则n ＝( )A ．m 3B ．m 2C ．9D ．8 4．给出下列各式：36a 3＝2a ，4a 2＋b 2＝a ＋b ，3－2＝6（－2）2，－342＝42（－3）4，其中正确的式子的个数是( )A ．0B ．1C ．2D ．35．若log 32＝a ，则log 38－2log 36用a 表示为( )A ．a －2B ．3a －(1＋a )2C ．5a －2D ．3a －2－a 26．化简5log25[(lg2)2＋lg 52]的结果是( )A ．lg 15B ．lg 5C ．lg 215 D ．lg 257．若a >1，b <0，且a b ＋a －b ＝22，则a b －a －b 的值等于( ) A. 6 B ．±2C ．－2D ．28．(1＋1322-) (1＋1162-) (1＋182-) (1＋142-) (1＋122-)＝( )A ．12(1－1322-)B ．12(1－1322-)－1C ．(1－1322-)－1D ．129．已知23a ＝49(a >0)________．10． (14)－2＋(16 2)0－327＝________． 11．已知x ，y ，z 都是大于1的正数，m >0，且log x m ＝24，log y m ＝40，log xyz m ＝12，则log z m ＝________． 12．(13分)化简下列各式：(1)(x －1＋x ＋x 0) (12x -－12x )；(2) 222233----++x y x y－222233------x y x y ； (3)(a 3＋a －3)(a 3－a －3)÷[(a 4＋a －4＋1)(a －a －1)]．13．(12分)设a ，b ，c 是直角三角形的三边长，其中c 为斜边长，且c ≠1.求证：log (c ＋b )a ＋log (c －b )a ＝2log (c ＋b )a ·log (c －b )a .课时作业(八)B [第8讲 指数与对数的运算](时间：30分钟 分值：80分)1．给出下列四个式子： ①6（－27）2＝±3；②3－2x 2＝(16x 8)112； ③7a 7＋b 7＝a ＋b ；④10（－2）5x 10y 15＝－|x |y ·－2y (y <0)． 其中错误的有( )A ．1个B ．2个C ．3个D ．4个2．化简2－(2k ＋1)－2－(2k －1)＋2－2k 等于( )A ．2－2kB ．2－(2k －1)C ．－2－(2k ＋1)D ．23．52532log 125－＝________．4．(log 23＋log 89)(log 34＋log 98＋log 32)＝________．5．对任意实数x ，下列等式恒成立的是( )A ．1223⎛⎫ ⎪⎝⎭x ＝13xB ．2132x ⎛⎫ ⎪⎝⎭＝13x C ．1335x ⎛⎫ ⎪⎝⎭＝15x D ．3153x --⎛⎫ ⎪⎝⎭＝15x 61142⎛⎫ ⎪⎝⎭a b (a ，b ＞0)的结果是( ) A.b a B ．abC.a b D ．a 2b7．若log 513·log 36·log 6x ＝2，则x ＝( )A.15B.125C ．lg 15D ．lg 1258．若lg a ，lg b 是方程2x 2－4x ＋1＝0的两个实根，则(lg a b )2的值等于( )A ．2B ．12C ．4D ．149．化简：4111442111244-⎛⎫- ⎪ ⎪ ⎪-⎝⎭a b b a a b ＝________． 10．若log a x ＝1，log b x ＝2，log c x ＝4，则log abc x ＝________．11．若log 1227＝a ，则log 616的值为用a 表示________．12．(13分)计算下列各题：(1)log 225·log 322·log 59；(2)(log 29＋log 419)(log 32＋log 90.5)； (3)lg(3＋5＋3－5)；(4)log 2(1＋32)＋log 2(1－32)；(5)(lg 5)2＋lg 2·lg 5＋lg 2；(6)lg 5(lg 8＋lg 1000)＋2＋lg 16＋lg 0.06.13．(12分)当x >0，y >0，且x (x ＋y )＝3 y (x ＋5y )时，求2x ＋xy ＋3yx ＋xy －y 的值．课时作业(八)A1．D 2．C 3．C 4．A 5．A 6．B 7．C 8．B 9．3 10．14 11．60 12．(1) 32x －32x (2)－23xy xy (3)a ＋1a 13．略课时作业(八)B1．C 2．C 3．1 4．152 5．C 6．C 7．B 8．A 9．a b10．47 11．4（3－a ）3＋a 12．(1)6 (2)12 (3)12 (4)－2 (5)1 (6)1 13．2薄雾浓云愁永昼， 瑞脑消金兽。

课时作业 (十五 ) [ 第 15 讲利用导数研究函数的最值、优化问题、方程与不等式 ](时间： 45 分钟分值：100分)1．函数 y＝xe x的最小值是 ()A ．－ 1B．－ e1C．－e D．不存在2．某城市在发展过程中，交通情况渐渐遇到关注，据相关统计数据显示，从上午 6 时到 9 时，车辆经过该市某一路段的用时 y(分钟 ) 与车辆进入该路段的时辰 t 之间的关系可近似地用以下函数给出： y1 332629＝－8t －4t ＋36t－4 .则在这段时间内，经过该路段用时最多的进入时辰是 ()A．6 时B．7 时C．8 时D．9 时3．[2013 ·河南十所名校联考 ] e，π分别是自然对数的底数和圆周率，则以下不等式中不建立的是()A.e>3πB．logπ e＋log eπ>1C．log e＋(log π)2>2πeeπD．e －e>e －π4． [2013 ·吉林实验中学模拟 ] 已知 f(x)＝x3－ 6x2＋ 9x－ abc，a<b<c，且 f(a)＝f(b)＝f(c)＝0.现给出以下结论：①f(0)f(1)>0；②f(0)f(1)<0；③f(0)f(3)>0；④f(0)f(3)<0；⑤abc<4；⑥a bc>4.此中正确结论的序号是()A ．①③⑤B．①④⑥C．②③⑤D．②④⑥5．定义在R上的可导函数f(x)知足 f(－x)＝f(x)，f(x－2)＝f(x＋2)，且当 x∈[0，2]时， f(x)＝ e x＋12xf′(0)，则 f(27)与 f(163)的大小关系是()716A ．f(2>f( 3 )716B．f(2＝f( 3 )716C．f(2<f( 3 )D．不确立1π6．[2013 ·郑州二检 ] 已知函数 f(x)＝2x－cos x，则方程 f(x)＝4的全部根的和为 ()ππ3πA．0 B.4 C.2 D.27．[2013·青岛一模 ]已知函数 f(x)＝2x－1，关于知足 0<x1<x2<2的随意 x1，x2，给出以下结论：①(x2－x1)[f(x2)－f(x1)]<0 ；②x2f(x1)<x1f(x2)；③f(x2)－f(x1)>x1－x2；④f（ x1）＋f（ x2）>f(x1＋x2).22此中正确结论的序号是()A ．①②B．①③C．②④D．③④8．[2013 ·日照二模 ] 已知定义在R上的可导函数 f(x)的导函数为f′(x)，知足 f′(x)<f(x)，且 f(x＋2)为偶函数， f(4)＝1，则不等式 f(x)<e x 的解集为 ()A ．(－2，＋∞ )B．(0，＋∞ )C．(1，＋∞ )D．(4，＋∞ )3－3x 在(a，6－a2上有最小值，．·厦门质检]若函数f(x)＝x)9 [2013则实数 a 的取值范围是 ()A ．(－ 5，1)B．[－ 5，1)C．[－2，1)D．(－2，1)10．[2013 ·长春四调 ] 已知函数 f(x)＝x3＋2x·f′(－1)，则 f(x)在区间 [ －2，3]上的值域是 ________．图 K15- 111．[2013 ·宁波五校联考 ] 已知函数 f′(x)，g′(x)分别是二次函数f(x)和三次函数 g(x)的导函数，它们在同一坐标系内的图像如图 K15-1所示．设函数 h(x)＝f(x)－g(x)，则 h(－1)，h(0)，h(1)的大小关系为____________________用(“<连”接 )．12．[2013 ·江苏镇江一模] 在平面直角坐标系xOy 中，已知A(1，0)，函数 y＝e x的图像与 y 轴的交点为 B，P 为函数 y＝e x图像上的任→→意一点，则 OP·AB的最小值为 ________．13．[2013 ·德州模拟 ] 已知函数 f(x)＝xe x，g(x)＝－ (x＋1)2＋a.若存在x1，x2∈R，使得f(x2)≤g(x1)建立，则实数 a 的取值范围是________．12 14．(10 分)[2013 陕·西西工大附中模拟 ] 已知函数 f(x)＝2ax － (2a＋1)x＋2ln x(a∈R)．(1)若曲线 y＝f(x)在 x＝1 和 x＝3 处的切线相互平行，求 a 的值及函数 f(x)的单一区间；(2)设 g(x)＝(x2－2x)e x，若对随意 x1∈(0，2]，均存在 x2∈(0，2]，使得 f(x1)<g(x2)，求 a 的取值范围．15．(13 分)某商场销售某种商品的经验表示，该商品每天的销售a量 y(单位：千克 )与销售价钱 x(单位：元 /千克 )知足关系式 y＝x－3＋10(x－6)2，此中 3<x<6，a 为常数．已知销售价钱为 5 元/千克时，每天可售出该商品 11 千克．(1)求 a 的值；(2)若该商品的成本为 3 元/千克，试确立销售价钱 x 的值，使商场每天销售该商品所获取的收益最大．a16．(12 分)[2013 琼·海模拟 ] 已知函数φ(x)＝x＋1，a 为正常数．9(1)若 f(x)＝ln x＋φ(x)，且 a＝2，求函数 f(x)的单一递加区间；(2)若 g(x)＝|ln x|＋φ(x)，且对随意 x1， x2∈(0，2]，x1≠x2，都有g（x2）－ g（x1）<－1，求 a 的取值范围．x2－x1课时作业 (十五 )1．C 2.C 3.D 4.C 5.C 6.C 7.D 8.B 9.C 10.[－42，9] 11.h(0)<h(1)<h(－1) 12.1113. －e，＋∞14．(1)a＝2函数 f(x)的单一递加区间为0，3，(2，＋∞ )，单323调递减区间为2，2(2)a>ln 2－115．(1)a＝2 (2)4 元/千克127 16．(1)函数 f(x)的单一递加区间为 (0，2)，(2，＋∞ ) (2)a≥2。

第三章 导数及其应用 学案13 导数的概念及运算导学目标： 1.了解导数概念的实际背景，理解函数在一点处的导数的定义和导数的几何意义，理解导函数的概念．了解曲线的切线的概念.2.能根据导数定义，求函数y ＝C (C 为常数)，y ＝x ，y ＝x 2，y ＝1x ，y ＝x 的导数．熟记基本初等函数的导数公式(c ，x m (m 为有理数)，sin x ，cos x ，e x ，a x ，ln x ，log a x 的导数)，能利用基本初等函数的导数公式及导数的四则运算法则求简单函数的导数，能求简单的复合函数(仅限于形如f (ax ＋b ))的导数．自主梳理1．函数的平均变化率一般地，已知函数y ＝f (x )，x 0，x 1是其定义域内不同的两点，记Δx ＝x 1－x 0，Δy ＝y 1－y 0＝f (x 1)－f (x 0)＝f (x 0＋Δx )－f (x 0)，则当Δx ≠0时，商________________________＝ΔyΔx 称作函数y ＝f (x )在区间[x 0，x 0＋Δx ](或[x 0＋Δx ，x 0])的平均变化率．2．函数y ＝f (x )在x ＝x 0处的导数 (1)定义函数y ＝f (x)在点x 0处的瞬时变化率______________通常称为f (x )在x ＝x 0处的导数，并记作f ′(x 0)，即______________________________．(2)几何意义函数f (x )在点x 0处的导数f ′(x 0)的几何意义是过曲线y ＝f (x )上点(x 0，f (x 0))的____________．导函数y ＝f ′(x )的值域即为__________________． 3．函数f (x )的导函数如果函数y ＝f (x )在开区间(a ，b )内每一点都是可导的，就说f (x )在开区间(a ，b )内可导，其导数也是开区间(a ，b )内的函数，又称作f (x )的导函数，记作____________．4．基本初等函数的导数公式表5．导数运算法则 (1)[f (x )±g (x )]′＝__________； (2)[f (x )g (x )]′＝______________； (3)⎣⎢⎡⎦⎥⎤f (x )g (x )′＝______________ [g (x )≠0]． 6．复合函数的求导法则：设函数u ＝φ(x )在点x 处有导数u x ′＝φ′(x )，函数y ＝f (u )在点x 处的对应点u 处有导数y u ′＝f ′(u )，则复合函数y ＝f (φ(x ))在点x 处有导数，且y ′x ＝y ′u ·u ′x ，或写作f ′x (φ(x ))＝f ′(u )φ′(x )．自我检测1．在曲线y ＝x 2＋1的图象上取一点(1,2)及附近一点(1＋Δx ，2＋Δy )，则ΔyΔx 为 ( )A ．Δx ＋1Δx ＋2B ．Δx －1Δx －2C ．Δx ＋2D ．2＋Δx －1Δx 2．设y ＝x 2·e x ，则y ′等于 ( )A ．x 2e x ＋2xB ．2x e xC ．(2x ＋x 2)e xD ．(x ＋x 2)·e x3．(2010·全国Ⅱ)若曲线y ＝x －12在点(a ，a －12)处的切线与两个坐标轴围成的三角形的面积为18，则a 等于 ( )A ．64B ．32C ．16D ．8 4．(2011·临汾模拟)若函数f (x )＝e x ＋a e －x 的导函数是奇函数，并且曲线y ＝f (x )的一条切线的斜率是32，则切点的横坐标是( ) A ．－ln 22B ．－ln 2C.ln 22D ．ln 25．(2009·湖北)已知函数f (x )＝f ′(π4)cos x ＋sin x ，则f (π4)＝________.探究点一 利用导数的定义求函数的导数 例1 利用导数的定义求函数的导数：(1)f (x )＝1x 在x ＝1处的导数；(2)f (x )＝1x ＋2.变式迁移1 求函数y ＝x 2＋1在x 0到x 0＋Δx 之间的平均变化率，并求出其导函数．探究点二 导数的运算例2 求下列函数的导数：(1)y ＝(1－x )⎝⎛⎭⎪⎫1＋1x ；(2)y ＝ln xx ；(3)y ＝x e x ；(4)y ＝tan x .变式迁移2 求下列函数的导数：(1)y ＝x 2sin x ；(2)y ＝3x e x －2x＋e ；(3)y ＝ln x x 2＋1.探究点三 求复合函数的导数 例3 (2011·莆田模拟)求下列函数的导数：(1)y ＝(1＋sin x )2；(2)y ＝11＋x 2； (3)y ＝ln x 2＋1；(4)y ＝x e 1－cos x .变式迁移3 求下列函数的导数：(1)y ＝1(1－3x )4；(2)y ＝sin 2⎝ ⎛⎭⎪⎫2x ＋π3；(3)y ＝x 1＋x 2.探究点四 导数的几何意义例4 已知曲线y ＝13x 3＋43.(1)求曲线在点P (2,4)处的切线方程； (2)求曲线过点P (2,4)的切线方程；(3)求满足斜率为1的曲线的切线方程．变式迁移4 求曲线f (x )＝x 3－3x 2＋2x 过原点的切线方程．1．准确理解曲线的切线，需注意的两个方面：(1)直线与曲线公共点的个数不是切线的本质特征，若直线与曲线只有一个公共点，则直线不一定是曲线的切线，同样，若直线是曲线的切线，则直线也可能与曲线有两个或两个以上的公共点．(2)曲线未必在其切线的“同侧”，如曲线y ＝x 3在其过(0,0)点的切线y ＝0的两侧．2．曲线的切线的求法：若已知曲线过点P (x 0，y 0)，求曲线过点P 的切线则需分点P (x 0，y 0)是切点和不是切点两种情况求解．(1)点P (x 0，y 0)是切点的切线方程为y －y 0＝f ′(x 0)(x －x 0)． (2)当点P (x 0，y 0)不是切点时可分以下几步完成： 第一步：设出切点坐标P ′(x 1，f (x 1))；第二步：写出过P ′(x 1，f (x 1))的切线方程为y －f (x 1)＝f ′(x 1)(x －x 1)；第三步：将点P 的坐标(x 0，y 0)代入切线方程求出x 1；第四步：将x 1的值代入方程y －f (x 1)＝f ′(x 1)(x －x 1)可得过点P (x 0，y 0)的切线方程．3．求函数的导数要准确地把函数分割为基本初等函数的和、差、积、商及其复合运算，再利用运算法则求导数．在求导过程中，要仔细分析函数解析式的结构特征，紧扣法则，联系基本初等函数求导公式，对于不具备求导法则结构形式的要适当变形．(满分：75分)一、选择题(每小题5分，共25分)1．已知函数f (x )＝2ln(3x )＋8x ，则0lim →∆x f (1－2Δx )－f (1)Δx的值为 ( )A ．10B ．－10C ．－20D ．20 2．(2011·温州调研)如图是函数f (x )＝x 2＋ax ＋b 的部分图象，则函数g (x )＝ln x ＋f ′(x )的零点所在的区间是 ( )A.⎝ ⎛⎭⎪⎫14，12B ．(1,2)C.⎝ ⎛⎭⎪⎫12，1 D ．(2,3)3．若曲线y ＝x 4的一条切线l 与直线x ＋4y －8＝0垂直，则l 的方程为 ( )A ．4x －y －3＝0B ．x ＋4y －5＝0C ．4x －y ＋3＝0D ．x ＋4y ＋3＝04．(2010·辽宁)已知点P 在曲线y ＝4e x ＋1上，α为曲线在点P 处的切线的倾斜角，则α的取值范围是 ( )A.⎣⎢⎡⎭⎪⎫0，π4B.⎣⎢⎡⎭⎪⎫π4，π2C.⎝ ⎛⎦⎥⎤π2，3π4D.⎣⎢⎡⎭⎪⎫3π4，π 5．(2011·珠海模拟)在下列四个函数中，满足性质：“对于区间(1,2)上的任意x 1，x 2 (x 1≠x 2)，|f (x 2)－f (x 1)|<|x 2－x 1|恒成立”的只有 ( )A ．f (x )＝1x B ．f (x )＝|x | x 26．一质点沿直线运动，如果由始点起经过t 秒后的位移为s ＝13t 3－32t 2＋2t ，那么速度为零的时刻是__________．7．若点P 是曲线f (x )＝x 2－ln x 上任意一点，则点P 到直线y ＝x －2的最小距离为________．8．设点P 是曲线y ＝x 33－x 2－3x －3上的一个动点，则以P 为切点的切线中，斜率取得最小值时的切线方程是__________________．三、解答题(共38分)9．(12分)求下列函数在x ＝x 0处的导数．(1)f (x )＝e x 1－x ＋e x1＋x ，x 0＝2；(2)f (x )＝x －x 3＋x 2ln xx 2，x 0＝1.10．(12分)(2011·保定模拟)有一个长度为5 m 的梯子贴靠在笔直的墙上，假设其下端沿地板以3 m/s 的速度离开墙脚滑动，求当其下端离开墙脚1.4 m 时，梯子上端下滑的速度．11．(14分)(2011·平顶山模拟)已知函数f (x )＝12x 2－a ln x (a ∈R )． (1)若函数f (x )的图象在x ＝2处的切线方程为y ＝x ＋b ，求a ，b 的值；(2)若函数f (x )在(1，＋∞)上为增函数，求a 的取值范围．自主梳理1.00()()f x x f x x+-△△2.（1）0lim x y x →△△△ 00'()lim x y f x x→=△△△ (2)切线的斜率 切线斜率的取值范围3.y ′或f ′(x)4．0 αx α－1cos x －sin x a xln a e x1x ln a 1x 5．(1)f ′(x )±g ′(x ) (2)f ′(x )g (x )＋f (x )g ′(x ) (3)f ′(x )g (x )－f (x )g ′(x )[g (x )]2自我检测1．C 2.C 3.A 4.D 5．1解析 ∵f ′(x )＝－f ′(π4)sin x ＋cos x ，∴f ′(π4)＝2－1.∴f (π4)＝1. 课堂活动区例1 解题导引 (1)用导数定义求函数导数必须把分式ΔyΔx 中的分母Δx 这一因式约掉才可能求出极限，所以目标就是分子中出现Δx ，从而分子分母相约分．(2)第(1)小题中用到的技巧是“分子有理化”．“有理化”是处理根式问题常用的方法，有时用“分母有理化”，有时用“分子有理化”．(3)注意在某点处的导数与导数定义式的区别：0000(()()'()limx f x x f x f x x→+-=△△△； 0()()'()lim x f x x f x f x x →+-=△△△； (4)用导数的定义求导的步骤为：①求函数的增量Δy ；②求平均变化率ΔyΔx ；③化简取极限．解 (1)Δy Δx ＝f (1＋Δx )－f (1)Δx=△△∴0'(1)lim lim x x y f x →→==△△△△ ＝－12.(2)Δy Δx ＝f (x ＋Δx )－f (x )Δx＝1122x x x x-+++△△＝(x ＋2)－(x ＋2＋Δx )Δx (x ＋2)(x ＋2＋Δx )＝－1(x ＋2)(x ＋2＋Δx )， ∴001'()lim lim (2)(2)x x y f x x x x x →→-==+++△△△△△ ＝－1(x ＋2)2.变式迁移1 解 ∵Δy ＝(x 0＋Δx )2＋1－x 20＋1＝(x 0＋Δx )2＋1－x 20－1(x 0＋Δx )2＋1＋x 20＋1＝2x 0Δx ＋(Δx )2(x 0＋Δx )2＋1＋x 20＋1， ∴ΔyΔx ＝2x0＋Δx (x 0＋Δx )2＋1＋x 20＋1. ∴yx =△△△ ∴y '=0lim limx x x →→=△△△△＝2x 2x 2＋1＝x x 2＋1. 例2 解题导引 求函数的导数要准确地把函数分割为基本函数的和、差、积、商及其复合运算，再利用运算法则求导数．在求导过程中，要仔细分析函数解析式的结构特征，紧扣求导法则，联系基本函数求导公式．对于不具备求导法则结构形式的要适当恒等变形．解 (1)∵y ＝(1－x )⎝⎛⎭⎪⎫1＋1x ＝1x－x ＝1122x x --，∴y ′＝1122()'()'x x --＝31221122x x ----.(2)y ′＝⎝ ⎛⎭⎪⎫ln x x ′＝(ln x )′x －x ′ln x x 2 ＝221ln 1ln x xx x x x--=. (3)y ′＝x ′e x ＋x (e x )′＝e x ＋x e x ＝e x (x ＋1)．(4)y ′＝⎝ ⎛⎭⎪⎫sin x cos x ′＝(sin x )′cos x －sin x (cos x )′cos 2x ＝cos x cos x －sin x (－sin x )cos 2x＝1cos 2x . 变式迁移2 解 (1)y ′＝(x 2)′sin x ＋x 2(sin x )′＝2x sin x ＋x 2cos x .(2)y ′＝(3x e x )′－(2x )′＋(e)′ ＝(3x )′e x ＋3x (e x )′－(2x )′＝3x ln 3·e x ＋3x e x －2x ln 2 ＝(ln 3＋1)(3e)x －2x ln 2.(3)y ′＝(ln x )′(x 2＋1)－ln x (x 2＋1)′(x 2＋1)2＝1x (x 2＋1)－ln x ·2x (x 2＋1)2＝x 2＋1－2x 2ln x x (x 2＋1)2.例3 解题导引 (1)求复合函数导数的思路流程为： 分解复合关系→分解复合关系→分层求导(2)由复合函数的定义可知，中间变量的选择应是基本函数的结构，解这类问题的关键是正确分析函数的复合层次，一般是从最外层开始，由外向内，一层一层地分析，把复合函数分解成若干个常见的基本函数，逐步确定复合过程．解 (1)y ′＝[(1＋sin x )2]′ ＝2(1＋sin x )·(1＋sin x )′ ＝2(1＋sin x )·cos x ＝2cos x ＋sin 2x .(2)y ′＝122(1)x -⎡⎤+⎢⎥⎣⎦′3222322(1)(1)'(1)x x x x --=++=-+=(3)y ′＝(ln x 2＋1)′＝1x 2＋1·(x 2＋1)′＝1x 2＋1·12(x 2＋1)－12·(x 2＋1)′＝x x 2＋1. 1cos 1cos 1cos 1cos 1cos 1cos 1cos 1cos (4)'()'()'[(1cos )']sin (1sin ).x x x x x xxx y xe e x e e x e x exexx x e --------==+=+-=+=+变式迁移3 解 (1)设u ＝1－3x ，y ＝u －4. 则y x ′＝y u ′·u x ′＝－4u －5·(－3)＝12(1－3x )5.(2)设y ＝u 2，u ＝sin v ，v ＝2x ＋π3，则y x ′＝y u ′·u v ′·v x ′＝2u ·cos v ·2＝4sin ⎝ ⎛⎭⎪⎫2x ＋π3·cos ⎝ ⎛⎭⎪⎫2x ＋π3 ＝2sin ⎝⎛⎭⎪⎫4x ＋2π3. (3)y ′＝(x 1＋x 2)′＝x ′·1＋x 2＋x (1＋x 2)′ ＝1＋x 2＋x 21＋x 2＝1＋2x 21＋x2. 例4 解题导引 (1)求曲线的切线要注意“过点P 的切线”与“在点P 处的切线”的差异；过点P 的切线中，点P 不一定是切点，点P 也不一定在已知曲线上，而在点P 处的切线，必以点P 为切点．(2)求函数对应曲线在某一点处的切线的斜率，只要求函数在该点处的导数即可．(3)解决“过某点的切线”问题，一般是设出切点坐标解决． 解 (1)∵y ′＝x 2，∴在点P (2,4)处的切线的斜率k ＝y ′|x ＝2＝4.∴曲线在点P (2,4)处的切线方程为y －4＝4(x －2)，即4x －y －4＝0.(2)设曲线y ＝13x 3＋43与过点P (2,4)的切线相切于点A ⎝ ⎛⎭⎪⎫x 0，13x 30＋43，则切线的斜率k ＝y ′|x ＝x 0＝x 20.∴切线方程为y －⎝ ⎛⎭⎪⎫13x 30＋43＝x 20(x －x 0)， 即y ＝x 20x －23x 30＋43.∵点P (2,4)在切线上，∴4＝2x 20－23x 30＋43，即x 30－3x 20＋4＝0，∴x 30＋x 20－4x 20＋4＝0，∴x 20(x 0＋1)－4(x 0＋1)(x 0－1)＝0，∴(x 0＋1)(x 0－2)2＝0，解得x 0＝－1或x 0＝2，故所求切线方程为4x －y －4＝0或x －y ＋2＝0.(3)设切点为(x 0，y 0)，则切线的斜率为k ＝x 20＝1，解得x 0＝±1，故切点为⎝ ⎛⎭⎪⎫1，53，(－1,1)． 故所求切线方程为y －53＝x －1和y －1＝x ＋1，即3x －3y ＋2＝0和x －y ＋2＝0.变式迁移4 解 f ′(x )＝3x 2－6x ＋2.设切线的斜率为k .(1)当切点是原点时k ＝f ′(0)＝2，所以所求曲线的切线方程为y ＝2x .(2)当切点不是原点时，设切点是(x 0，y 0)，则有y 0＝x 30－3x 20＋2x 0，k ＝f ′(x 0)＝3x 20－6x 0＋2，①又k ＝y 0x 0＝x 20－3x 0＋2，② 由①②得x 0＝32，k ＝－14.∴所求曲线的切线方程为y ＝－14x .综上，曲线f (x )＝x 3－3x 2＋2x 过原点的切线方程为y ＝2x 或y ＝－14x .课后练习区1．C 2.C 3.A 4.D 5.A6．1秒或2秒末7. 28．12x ＋3y ＋8＝0 9．解 (1)∵f ′(x )＝⎝ ⎛⎭⎪⎫2e x 1－x ′＝(2e x )′(1－x )－2e x (1－x )′(1－x )2 ＝2(2－x )e x(1－x )2，∴f ′(2)＝0.………………………………………………………………(6分)(2)∵f ′(x )＝(x －32)′－x ′＋(ln x )′＝－32x －52－1＋1x ，∴f ′(1)＝－32.……………………………………………………(12分)10．解 设经时间t 秒梯子上端下滑s 米，则s ＝5－25－9t 2，当下端移开 1.4 m 时，……………………………………………………………………(3分)t 0＝ 1.43＝715，……………………………………………………………………………(5分)又s ′＝－12(25－9t 2)－12·(－9·2t )＝9t ·125－9t 2，…………………………………………………………………………(10分)所以s ′(t 0)＝9×715·125－9×⎝ ⎛⎭⎪⎫7152＝0.875 (m /s )．故所求的梯子上端下滑的速度为0.875 m /s .……………………………………………(12分)11．解 (1)因为f ′(x )＝x －a x(x >0)，……………………………………………………(2分)又f(x )在x ＝2处的切线方程为y ＝x ＋b ，所以⎩⎨⎧2－a ln 2＝2＋b ，2－a 2＝1，……………………………………………………………（5分）解得a ＝2，b ＝－2ln2.……………………………………………………………………(7分)(2)若函数f (x)在(1，＋∞)上为增函数，则f ′(x )＝x －a x ≥0在(1，＋∞)上恒成立，……………………………………………(10分)即a ≤x 2在(1，＋∞)上恒成立．所以有a ≤1.……………………………………………………………………………(14分)。