2019-2020年高三数学二模试题 理 新人教A版

2019-2020年高三数学第二次适应性检测理新人教A版注意事项：1．本试卷分第I卷选择题．和第Ⅱ卷非选择题．两部分。

答题前，考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。

2．回答第I卷时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号。

写在本试卷上无效。

3．回答第Ⅱ卷时，将答案写在答题卡上，写在本试卷上无效。

4．考试结束后，将本试卷和答题卡一并交回。

第I卷一、选择题：本大题共12小题，每小题5分，每小题给出的四个选项中，只有一项是符合题目要求的。

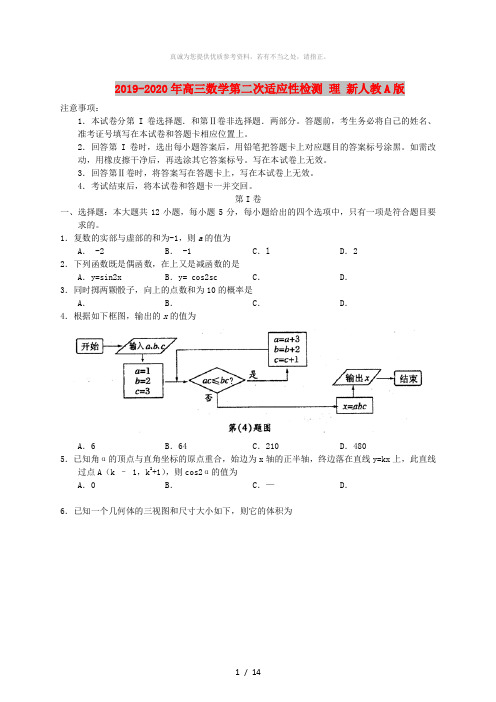
1．复数的实部与虚部的和为-1，则a的值为A． -2 B． -1 C．l D．22．下列函数既是偶函数，在上又是减函数的是A．y=sin2x B．y= cos2sc C．D．3．同时掷两颗骰子，向上的点数和为10的概率是A．B．C．D．4．根据如下框图，输出的x的值为A．6 B．64 C．210 D．4805．已知角α的顶点与直角坐标的原点重合，始边为x轴的正半轴，终边落在直线y=kx上，此直线过点A（k – 1，k2+1），则cos2α的值为A．0 B．C．—D．6．已知一个几何体的三视图和尺寸大小如下，则它的体积为A ．B ．C ．D ．7．设{a n }为公比q>1的等比数列，若，是方程4x 2—8x +3 =0的两根，则等于A ．6B ．18C ．54D ．8．已知的最大值为n ，则二项式展开式中常数项等于A ．21B ．28C ．36D ．459．由曲线y=x 2 +2和直线y=3x 所围成的平面图形的面积为A ．B ．C ．D ．10．已知双曲线的左顶点是圆的圆心，一条渐近线的方程为y=2x ，则双曲线的焦距为A ．5B ．C ．D ．11．已知A 、B 、C 是圆上三点，且等于A ．0B ．C ．D ．—12．半径为1的球内切于一圆锥，则圆锥体积的最小值为A ．B ．C ．D ．第Ⅱ卷本卷包括必考题和选考题两部分。

2019-2020年高三下学期第二次模拟考试数学（理）试题含解析第Ⅰ卷（共50分）一、选择题：本大题共12个小题,每小题5分,共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.若集合{}1,1A =-，{}0,2B =，则集合{},,z z x y x A y B =+∈∈中的元素的个数为（ ）A ．5 B.4 C.3 D.22.复数131i Z i-=+的实部是 （ ） A ． 2 B ． 1 C ．1- D ．4-3.在等差数列{}n a 中，1315310a a a ++=，则5a 的值为（ ）A ．2B ．3C ．4D ．5【答案】A【解析】试题分析：设等差数列{}n a 的公差为d ，则131511115333214520510a a a a a d a d a d a ++=++⨯++=+==，则52a =．考点：等差数列的运算．4.条件:12p x +>，条件:2q x ≥，则p ⌝是q ⌝的（ ）A ．充分非必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要的条件5.已知双曲线2222:1(,0)x y C a b a b-=>的左、右焦点分别为1F ，2F ,过2F 作双曲线C 的一条渐近线的垂线,垂足为H ,若2F H 的中点M 在双曲线C 上,则双曲线C 的离心率为（ ）6.运行右图所示框图的相应程序,若输入,a b 的值分别为2log 3和3log 2,则输出M 的值是（ ）A.0B.1C. 2D. －1【答案】C【解析】 试题分析：因为2log 31>，3log 21<，所以23log 3log 2>，由算法框图可知，运行后输出M 的值为23log 3log 21112M =⋅+=+=．考点：算法框图． 7.一个空间几何体的三视图如图所示，则该几何体的表面积为（ ）A ． 48B ．32817+C ．48817+D ．80【答案】C【解析】试题分析：如图所示的三视图是以左视图所示等腰梯形为底的直四棱柱，其底面上底长为2，下底长为4，高为4，故底面积()11244122S =+⨯=，腰长为：221417+=，则底面周长为：242176217++=+，则其侧面积()26217424817S =+⨯=+，则该几何体的表面积为1222122481748817S S +=⨯++=+，故选C ．考点：三视图，几何体的表面积．8.△ABC 的三个内角A ，B ，C 所对的边分别为a ，b ，c ，a A b B A a 2cos sin sin 2=+，则=ab （ ） A 2 B ．223 D ．39.设第一象限内的点(,)x y 满足约束条件26020x y x y --≤⎧⎨-+≥⎩，若目标函数(0,z ax by a =+>0)b >的最大值为40，则51a b +的最小值为（ ） （A ）256 （B ）94（C ）1 （D ）4考点：简单线性规划, 基本不等式.10.规定[]x 表示不超过x 的最大整数，例如：[3.1]=3，[-2.6]=-3，[-2]=-2；若()f x '是函数()ln ||f x x =导函数，设()()()g x f x f x '=⋅，则函数[()][()]y g x g x =+-的值域是（ ）A ．{}偶数B ．{0,1}C ．{0} D.{1,0}-第Ⅱ卷（共100分）二、填空题（每题5分，满分25分，将答案填在答题纸上） 11.已知向量()3,1a =r ，()0,1b =-r ，(),3c k =r ．若()2a b -r r 与c r 共线，则k =________.12.观察下列式子：2222221311511171,1,1222332344+<++<+++<,…,根据以上 式子可以猜想：2222111112342011+++<L L _________;13.函数2221()431x x f x x x x -⎧=⎨-+>⎩， ≤， 的图象和函数()()ln 1g x x =-的图象的交点个数是。

2019-2020年高考数学二模试卷（理科）含解析一、选择题：本大题共8小题，每小题5分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.1．若￢p∨q是假命题，则（）A．p∧q是假命题B．p∨q是假命题C．p是假命题D．￢q是假命题2．下列四个函数中，既是奇函数又在定义域上单调递增的是（）A．y=x﹣1 B．y=tanx C．y=x3D．y=log2x3．如图，A，B，C，D是⊙O上的四个点，过点B的切线与DC的延长线交于点E．若∠BCD=110°，则∠DBE=（）A．75°B．70°C．60°D．55°4．设平面向量=（1，2），=（﹣2，y），若∥，则|2﹣|等于（）A．4 B．5 C．D．5．已知M，N是不等式组所表示的平面区域内的两个不同的点，则|MN|的最大值是（）A．B．C．D．6．已知数列{a n}的前n项和为S n，a1=1，2S n=a n+1，则S n=（）A．2n﹣1B．2n﹣1 C．3n﹣1D．7．一个几何体的三视图如图所示，则这个几何体的表面积为（）A．B．C．D．98．定义运算，称为将点（x，y）映到点（x′，y′）的一次变换．若=把直线y=kx上的各点映到这点本身，而把直线y=mx上的各点映到这点关于原点对称的点．则k，m，p，q的值依次是（）A．k=1，m=﹣2，p=3，q=3 B．k=1，m=3，p=3，q=﹣2C．k=﹣2，m=3，p=3，q=1 D．k=﹣2，m=1，p=3，q=3二、填空题：本大题共6小题，每小题5分，共30分.9．在复平面内，复数i（2﹣i）对应的点的坐标为．10．直线l的参数方程为（t为参数），则直线l的斜率为．11．在△ABC中，角A，B，C所对的边分别是a，b，c.，则tanB=．12．若展开式中的二项式系数和为64，则n等于，该展开式中的常数项为．13．抛物线C：y2=2px的焦点坐标为，则抛物线C的方程为，若点P在抛物线C上运动，点Q在直线x+y+5=0上运动，则|PQ|的最小值等于．14．在数列{a n}中，如果对任意的n∈N*，都有﹣=λ（λ为常数），则称数列{a n}为比等差数列，λ称为比公差．现给出以下命题：①若数列{F n}满足F1=1，F2=1，F n=F n﹣1+F n﹣2（n≥3），则该数列不是比等差数列；②若数列{a n}满足，则数列{a n}是比等差数列，且比公差λ=0；③等比数列一定是比等差数列，等差数列一定不是比等差数列；④若{a n}是等差数列，{b n}是等比数列，则数列{a n b n}是比等差数列．其中所有真命题的序号是．三、解答题：本大题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程.15．已知函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π）的最小正周期为π，且图象过点．（Ⅰ）求ω，φ的值；（Ⅱ）设，求函数g（x）的单调递增区间．16．如图，ABCD是正方形，DE⊥平面ABCD，AF∥DE，DE=DA=3AF．（Ⅰ）求证：AC⊥BE；（Ⅱ）求二面角F﹣BE﹣D的余弦值；（Ⅲ）设点M是线段BD上一个动点，试确定点M的位置，使得AM∥平面BEF，证明你的结论．17．小明从家到学校有两条路线，路线1上有三个路口，各路口遇到红灯的概率均为；路线2上有两个路口，各路口遇到红灯的概率依次为．（Ⅰ）若小明上学走路线1，求最多遇到1次红灯的概率；（Ⅱ）若小明上学走路线2，求遇到红灯次数X的数学期望；（Ⅲ）按照“平均遇到红灯次数越少为越好”的标准，请你帮助小明从上述两条路线中选择一条最好的上学路线，并说明理由．18．已知函数（a＞0）．（Ⅰ）当a=1时，求函数f（x）的单调区间；（Ⅱ）当x=﹣5时，f（x）取得极值．①若m≥﹣5，求函数f（x）在上的最小值；②求证：对任意x1，x2∈，都有|f（x1）﹣f（x2）|≤2．19．已知椭圆C：的离心率为，且过点．直线交椭圆C于B，D（不与点A重合）两点．（Ⅰ）求椭圆C的方程；（Ⅱ）△ABD的面积是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．20．设m＞3，对于项数为m的有穷数列{a n}，令b k为a1，a2，a3…a k（k≤m）中的最大值，称数列{b n}为{a n}的“创新数列”．例如数列3，5，4，7的创新数列为3，5，5，7．考查自然数1、2…m（m＞3）的所有排列，将每种排列都视为一个有穷数列{c n}．（Ⅰ）若m=5，写出创新数列为3，5，5，5，5的所有数列{c n}；（Ⅱ）是否存在数列{c n}的创新数列为等比数列？若存在，求出符合条件的创新数列；若不存在，请说明理由；（Ⅲ）是否存在数列{c n}，使它的创新数列为等差数列？若存在，求出所有符合条件的数列{c n}的个数；若不存在，请说明理由．xx北京市房山区高考数学二模试卷（理科）参考答案与试题解析一、选择题：本大题共8小题，每小题5分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.1．若￢p∨q是假命题，则（）A．p∧q是假命题B．p∨q是假命题C．p是假命题D．￢q是假命题考点：复合命题的真假．专题：常规题型．分析：由题意，可得￢p，q的真假性，进而得到正确选项．解答：由于￢p∨q是假命题，则￢p是假命题，q是假命题，所以p是真命题，q是假命题，所以p∧q是假命题，p∨q是真命题，￢q是真命题，故选A．点评：本题考查的知识点是复合命题的真假判定，解决的办法是先判断组成复合命题的简单命题的真假，再根据真值表进行判断．2．下列四个函数中，既是奇函数又在定义域上单调递增的是（）A．y=x﹣1 B．y=tanx C．y=x3D．y=log2x考点：奇偶性与单调性的综合．专题：综合题；函数的性质及应用．分析：根据函数的奇偶性、单调性逐项判断即可．解答：解：y=x﹣1非奇非偶函数，故排除A；y=tanx为奇函数，但在定义域内不单调，故排除B；y=log2x单调递增，但为非奇非偶函数，故排除D；令f（x）=x3，定义域为R，关于原点对称，且f（﹣x）=（﹣x）3=﹣x3=﹣f（x），所以f（x）为奇函数，又f（x）在定义域R上递增，故选C．点评：本题考查函数的奇偶性、单调性的判断，属基础题，定义是解决该类问题的基本方法，应熟练掌握．3．如图，A，B，C，D是⊙O上的四个点，过点B的切线与DC的延长线交于点E．若∠BCD=110°，则∠DBE=（）A．75°B．70°C．60°D．55°考点：与圆有关的比例线段．分析：利用四点共圆的性质可得∠A，再利用弦切角定理即可得出∠DBE=∠A．解答：解：∵A，B，C，D是⊙O上的四个点，∴∠A+∠BCD=180°，∵∠BCD=110°，∴∠A=70°．∵BE与⊙O相切于点B，∴∠DBE=∠A=70°．故选B．点评：熟练掌握四点共圆的性质、弦切角定理是解题的关键．4．设平面向量=（1，2），=（﹣2，y），若∥，则|2﹣|等于（）A．4 B．5 C．D．考点：平行向量与共线向量；向量的模．专题：平面向量及应用．分析：利用向量共线定理即可得出y，从而计算出的坐标，利用向量模的计算公式即可得出．解答：解：∵∥，∴﹣2×2﹣y=0，解得y=﹣4．∴=2（1，2）﹣（﹣2，﹣4）=（4，8），∴|2﹣|==．故选D．点评：熟练掌握向量共线定理、向量模的计算公式是解题的关键．5．已知M，N是不等式组所表示的平面区域内的两个不同的点，则|MN|的最大值是（）A．B．C．D．考点：简单线性规划；两点间的距离公式．专题：计算题；不等式的解法及应用．分析：作出题中不等式组表示的平面区域，得到如图的四边形ABCD．因为四边形ABCD的对角线BD是区域中最长的线段，所以当M、N分别与对角线BD的两个端点重合时，|MN|取得最大值，由此结合两点间的距离公式可得本题答案．解答：解：作出不等式组表示的平面区域，得到如图的四边形ABCD，其中A（1，1），B（5，1），C（，），D（1，2）∵M、N是区域内的两个不同的点∴运动点M、N，可得当M、N分别与对角线BD的两个端点重合时，距离最远因此|MN|的最大值是|BD|==故选：B点评：题给出二元一次不等式组表示的平面区域内动点M、N，求|MN|的最大值，着重考查了二元一次不等式组表示的平面区域和平面内两点间的距离公式等知识，属于基础题．6．已知数列{a n}的前n项和为S n，a1=1，2S n=a n+1，则S n=（）A．2n﹣1B．2n﹣1 C．3n﹣1D．考点：数列的求和．专题：等差数列与等比数列．分析：利用当n≥2时，2S n=a n+1，2S n﹣1=a n，两式相减得3a n=a n+1，再利用等比数列的前n项和公式即可得出，n=1时单独考虑．解答：解：当n=1时，∵a1=1，2S1=a2，∴a2=2．当n≥2时，由2S n=a n+1，2S n﹣1=a n，两式相减得2a n=a n+1﹣a n，∴a n+1=3a n，∴数列{a n}是以a2=2，3为公比的等比数列，∴=3n﹣1，当n=1时，上式也成立．故选C．点评：熟练掌握a n=S n﹣S n﹣1（n≥2）及等比数列的前n项和公式是解题的关键．7．一个几何体的三视图如图所示，则这个几何体的表面积为（）A．B．C．D．9考点：由三视图求面积、体积．专题：计算题．分析：判断三视图对应的几何体的形状，利用三视图的数据求解几何体的表面积即可．解答：解：三视图复原的几何体是长方体的一个角，如图：直角顶点处的三条棱长：3，，3．其中斜侧面的高为：3．几何体的表面积是：=．故选A．点评：本题考查三视图与几何体的关系，判断几何体的形状是解题的关键．8．定义运算，称为将点（x，y）映到点（x′，y′）的一次变换．若=把直线y=kx上的各点映到这点本身，而把直线y=mx上的各点映到这点关于原点对称的点．则k，m，p，q的值依次是（）A．k=1，m=﹣2，p=3，q=3 B．k=1，m=3，p=3，q=﹣2C．k=﹣2，m=3，p=3，q=1 D．k=﹣2，m=1，p=3，q=3考点：几种特殊的矩阵变换．专题：新定义．分析：设（1，k）是曲线y=kx上的点，在矩阵的作用下的点为（1，k），再设（1，m）是曲线y=mx上的点，在矩阵的作用下的点为（﹣1，﹣m），得出关于k，m，p，q的方程组，从而解决问题．解答：解：设（1，k）是曲线y=kx上的点，在矩阵的作用下的点为（1，k），即①设（1，m）是曲线y=mx上的点，在矩阵的作用下的点为（﹣1，﹣m），∴②．由①②得k=1，m=3，p=3，q=﹣2故选B．点评：本小题主要考查几种特殊的矩阵变换、曲线与方程等基础知识，考查运算求解能力，解答的关键是利用待定系数法求解，属于基础题．二、填空题：本大题共6小题，每小题5分，共30分.9．在复平面内，复数i（2﹣i）对应的点的坐标为（1，2）．考点：复数的代数表示法及其几何意义．专题：计算题．分析：利用复数的运算法则化为1+2i，再利用复数的几何意义可得到复数i（2﹣i）对应的点的坐标．解答：解：∵复数i（2﹣i）=1+2i．∴复数i（2﹣i）对应的点的坐标为（1，2）．故答案为（1，2）．点评：熟练掌握复数的运算法则、复数的几何意义是解题的关键．10．直线l的参数方程为（t为参数），则直线l的斜率为．考点：参数方程化成普通方程．专题：计算题．分析：先将利用消参法将直线的参数方程化成直线的普通方程，再将直线写出斜截式，求出斜率即可．解答：解：∵直线l的参数方程为（t为参数）∴消去参数t得y﹣1=（x﹣1）则直线l的斜率为，故答案为：．点评：本题主要考查了直线的参数方程，以及直线的斜率等基础知识，属于基础题．11．在△ABC中，角A，B，C所对的边分别是a，b，c.，则tanB=．考点：正弦定理；同角三角函数间的基本关系．专题：计算题；解三角形．分析：根据正弦定理，算出sinB==，由b＜a得B是锐角，利用同角三角函数的平方关系算出cosB=，再用商数关系算出tanB=，即可得到本题答案．解答：解：∵∴由正弦定理，得sinB==∵b＜a可得B是锐角，∴cosB==，因此，tanB===故答案为：点评：本题给出三角形ABC的两边和其中一边的对角，求另一个角的正切之值，着重考查了利用正弦定理解三角形和同角三角函数基本关系等知识，属于基础题．12．若展开式中的二项式系数和为64，则n等于6，该展开式中的常数项为15．考点：二项式系数的性质．专题：计算题．分析：由题意可得得2n=64，求得n=6．在展开式的通项公式中，令x的幂指数等于零，求得r的值，即可求得展开式中的常数项．解答：解：由展开式中的二项式系数和为64，可得2n=64，∴n=6．由于=，展开式的通项公式为T r+1=•x12﹣2r•x﹣r=•x12﹣3r，令12﹣3r=0，r=4，故该展开式中的常数项为==15，故答案为6，15．点评：本题主要考查二项式定理的应用，二项展开式的通项公式，求展开式中某项的系数，二项式系数的性质，属于中档题．13．抛物线C：y2=2px的焦点坐标为，则抛物线C的方程为y2=2x，若点P在抛物线C上运动，点Q在直线x+y+5=0上运动，则|PQ|的最小值等于．考点：直线与圆锥曲线的关系；抛物线的简单性质．专题：圆锥曲线中的最值与范围问题．分析：由y2=2px的焦点坐标为，得，从而求得p值，设与直线x+y+5=0平行的抛物线的切线方程为x+y+m=0，直线x+y+5=0与切线距离即为|PQ|的最小值，联立切线方程与抛物线方程消掉x得y的二次方程，令△=0可求得m值，从而得切线方程，根据两点间距离公式即可求得答案．解答：解：因为y2=2px的焦点坐标为，所以p＞0，且，解得p=1，所以抛物线方程为y2=2x，设与直线x+y+5=0平行的抛物线的切线方程为x+y+m=0，由得y2+2y+2m=0，令△=0，即22﹣4×2m=0，解得m=，则切线方程为x+y+=0，两平行线间的距离d==，即为|PQ|的最小值．故答案分别为：y2=2x，．点评：本题考查直线与圆锥曲线的位置关系、抛物线的性质，考查转化思想，解决本题的关键把|PQ|的最小值转化为直线与抛物线切线间的距离求解．14．在数列{a n}中，如果对任意的n∈N*，都有﹣=λ（λ为常数），则称数列{a n}为比等差数列，λ称为比公差．现给出以下命题：①若数列{F n}满足F1=1，F2=1，F n=F n﹣1+F n﹣2（n≥3），则该数列不是比等差数列；②若数列{a n}满足，则数列{a n}是比等差数列，且比公差λ=0；③等比数列一定是比等差数列，等差数列一定不是比等差数列；④若{a n}是等差数列，{b n}是等比数列，则数列{a n b n}是比等差数列．其中所有真命题的序号是①②．考点：命题的真假判断与应用；等比关系的确定．专题：阅读型；新定义．分析：①斐波那契数列{F n}，根据斐波那契数列的性质进行化简变形，看其是否满足比等差数列的定义；②若a n=3•2n﹣1，代入﹣进行求解看是否是常数，可得答案；③根据等比数列的定义可知=，满足比等差数列的定义，若等差数列为a n=n，看其是否满足﹣=λ（λ为常数）；④如果{a n}是等差数列，{b n}是等比数列，设a n=n，b n=2n，看其是否满足比等差数列的定义．解答：解：①由题意知，数列{F n}为斐波那契数列{F n}，﹣=≠常数，不满足比等差数列的定义，故①正确；②若a n=3•2n﹣1，则﹣==0，满足比等差数列的定义，故②正确；③等比数列都有﹣=0，满足比等差数列的定义，若等差数列为a n=1，则有﹣=0，故③不正确；④如果{a n}是等差数列，{b n}是等比数列，设a n=n，b n=2n，则﹣=﹣==﹣≠常数，不满足比等差数列的定义，故④不正确；故答案为：①②点评：本题考查新定义，解题时应正确理解新定义，同时注意利用列举法判断命题为假，属于难题．三、解答题：本大题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程. 15．已知函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π）的最小正周期为π，且图象过点．（Ⅰ）求ω，φ的值；（Ⅱ）设，求函数g（x）的单调递增区间．考点：y=Asin（ωx+φ）中参数的物理意义；二倍角的正弦；正弦函数的单调性．专题：计算题；三角函数的图像与性质．分析：（Ⅰ）利用函数的周期公式求出ω，通过函数图象经过的点直接求解φ的值；（Ⅱ）化简的表达式，通过正弦函数的单调增区间，直接求函数g（x）的单调递增区间．解答：解：（Ⅰ）因为函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π）的最小正周期为π，所以T=，ω=2，图象过点．所以，0＜φ＜π，所以φ=．（Ⅱ）因为=sin（2x+）sin（2x﹣）=cos2xsin2x=sin4x，由2kπ，k∈Z得，所以函数的单调增区间为点评：本题考查三角函数的化简，函数的周期的求法，二倍角的正弦函数，函数的单调性的应用，考查计算能力．16．如图，ABCD是正方形，DE⊥平面ABCD，AF∥DE，DE=DA=3AF．（Ⅰ）求证：AC⊥BE；（Ⅱ）求二面角F﹣BE﹣D的余弦值；（Ⅲ）设点M是线段BD上一个动点，试确定点M的位置，使得AM∥平面BEF，证明你的结论．考点：用空间向量求平面间的夹角；直线与平面平行的判定．专题：计算题；证明题；空间角；空间向量及应用．分析：（I）在正方形ABCD中，可得AC⊥BD．根据DE⊥平面ABCD，得DE⊥AC，由线面垂直的判定定理可得AC⊥平面BDE，从而可得AC⊥BE；（II）分别以DADCDE为x轴、y轴、z轴，建立如图所求空间直角坐标系．设AD=3，则可得DE=3，AF=1，可得D、A、B、C、E和F各点的坐标，进而得到向量、的坐标，再利用垂直向量数量积为零建立方程组，解出平面BEF的一个法向量为=（2，1，3），而=（﹣3，3，0）是平面BDE的一个法向量，根据空间向量的夹角公式算出、所成的角余弦值，即可得到二面角F﹣BE﹣D的余弦值；（III）设M（t，t，0）（）．可得关于t的坐标形式，根据AM∥平面BEF，得⊥=0，由数量积为零建立关于t的方程，解之得t=1，从而得到当BM=BD时，AM∥平面BEF．解答：解：（Ⅰ）∵DE⊥平面ABCD，AC⊂平面ABCD，∴DE⊥AC．∵四边形ABCD是正方形，∴AC⊥BD，又∵BD、DE是平面BDE内的相交直线，∴AC⊥平面BDE，结合BE⊂平面BDE，得AC⊥BE；…（4分）（II）因为直线BD、BC、BE两两垂直，所以分别以DADCDE为x轴、y轴、z轴，建立如图所求空间直角坐标系设AD=3，则可得DE=3，AF=1因此，D（0，0，0），A（3，0，0），B（3，3，0），C（0，3，0），E（0，0，3），F（3，0，1）∴=（0，﹣3，1），=（3，0，﹣2）…（5分）设平面BEF的法向量为=（x，y，z），得，令z=3，得x=2且y=1，可得=（2，1，3），…（7分）∵AC⊥平面BDE，得=（﹣3，3，0）是平面BDE的一个法向量∴二面角F﹣BE﹣D的大小即为向量、所成角的大小（或其补角）∵cos===﹣∴结合图形加以观察，可得二面角F﹣BE﹣D的余弦值为|cos|=；…（10分）（Ⅲ）点M是线段BD上一个动点，根据（II）的结论，设M（t，t，0）（）．则=（t﹣3，t，0）．∵AM∥平面BEF，∴•=0，即2（t﹣3）+t=0，解之得t=2．…（12分）此时，点M坐标为（2，2，0），即当BM=BD时，AM∥平面BEF．…（14分）点评：本题给出四棱锥的一条侧棱与底面垂直且底面是正方形，求证线面垂直并求二面角的余弦值大小，着重考查了线面垂直、平行的判定与性质和利用空间向量研究平面与平面所成角的求法等知识，属于中档题．17．小明从家到学校有两条路线，路线1上有三个路口，各路口遇到红灯的概率均为；路线2上有两个路口，各路口遇到红灯的概率依次为．（Ⅰ）若小明上学走路线1，求最多遇到1次红灯的概率；（Ⅱ）若小明上学走路线2，求遇到红灯次数X的数学期望；（Ⅲ）按照“平均遇到红灯次数越少为越好”的标准，请你帮助小明从上述两条路线中选择一条最好的上学路线，并说明理由．考点：离散型随机变量的期望与方差；相互独立事件的概率乘法公式．专题：概率与统计．分析：（Ⅰ）走路线1最多遇到1次红灯为事件A，分为两种情况，一种是3次都没有遇到红灯，一种是只有一次遇到红灯，可知A～B，计算出即可；（Ⅱ）由题意可得，X可能取值为0，1，2．利用独立事件的概率计算公式和互斥事件的概率计算公式即可得出概率，再利用数学期望计算公式即可；（Ⅲ）设选择路线1遇到红灯次数为ξ，则ξ～B（3，），利用公式计算出Eξ与EX比较即可．解答：解：（Ⅰ）设走路线1最多遇到1次红灯为事件A，则P（A）==．（Ⅱ）由题意可得，X可能取值为0，1，2．∴P（X=0）==，P（X=1）==，P（X=2）=．∴随机变量X的分布列为遇到红灯次数X的数学期望EX==．（Ⅲ）设选择路线1遇到红灯次数为ξ，则ξ～B（3，），∴Eξ=．∵Eξ＜EX，∴选择路线1上学最好．点评：熟练掌握独立事件的概率计算公式、互斥事件的概率计算公式、数学期望计算公式、分类讨论思想方法、二项分布概率计算公式是解题的关键．18．已知函数（a＞0）．（Ⅰ）当a=1时，求函数f（x）的单调区间；（Ⅱ）当x=﹣5时，f（x）取得极值．①若m≥﹣5，求函数f（x）在上的最小值；②求证：对任意x1，x2∈，都有|f（x1）﹣f（x2）|≤2．考点：利用导数求闭区间上函数的最值；利用导数研究函数的极值．专题：综合题；导数的综合应用．分析：（Ⅰ）求导数f′（x），当a=1时，解不等式f′（x）＞0，f′（x）＜0即可；（Ⅱ）①当x=﹣5时f（x）取得极值可得f′（﹣5）=0，由此求得a值，从而利用导数可求得f（x）的单调区间及极值点，按极值点在区间内、外讨论f（x）的单调性，由单调性即可求得f（x）的最小值；②对任意x1，x2∈，都有|f（x1）﹣f（x2）|≤f max（x）﹣f min（x），利用导数易求得函数在内的最大值、最小值；解答：解：（Ⅰ）f′（x）=+（2x+1）=，当a=1时，f′（x）=x（x+3）e x，解f′（x）＞0得x＞0或x＜﹣3，解f′（x）＜0得﹣3＜x＜0，所以f（x）的单调增区间为（﹣∞，﹣3）和（0，+∞），单调减区间为（﹣3，0）．（Ⅱ）①当x=﹣5时，f（x）取得极值，所以f′（﹣5）=，解得a=2（经检验a=2符合题意），f′（x）=，当x＜﹣5或x＞0时f′（x）＞0，当﹣5＜x＜0时f′（x）＜0，所以f（x）在（﹣∞，﹣5）和（0，+∞）上递增，在（﹣5，0）上递减，当﹣5≤m≤﹣1时，f（x）在上单调递减，f min（x）=f（m+1）=m（m+3），当﹣1＜m＜0时，m＜0＜m+1，f（x）在上单调递减，在上单调递增，f min（x）=f（0）=﹣2，当m≥0时，f（x）在上单调递增，f min（x）=f（m）=（m+2）（m﹣1），综上，f（x）在上的最小值为；②令f′（x）=0得x=0或x=﹣5（舍），因为f（﹣2）=0，f（0）=﹣2，f（1）=0，所以f max（x）=0，f min（x）=﹣2，所以对任意x1，x2∈，都有|f（x1）﹣f（x2）|≤f max（x）﹣f min（x）=2．点评：本题考查利用导数研究函数的极值、最值，考查分类讨论思想，考查学生分析问题解决问题的能力，综合性强，难度较大．19．已知椭圆C：的离心率为，且过点．直线交椭圆C于B，D（不与点A重合）两点．（Ⅰ）求椭圆C的方程；（Ⅱ）△ABD的面积是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．考点：直线与圆锥曲线的综合问题；椭圆的标准方程．专题：圆锥曲线中的最值与范围问题．分析：（Ⅰ）利用椭圆的标准方程、离心率及a2=b2+c2即可得出；（2）把直线BD的方程与椭圆的方程联立，利用根与系数的关系及弦长公式即可得到|BD|，利用点到直线的距离公式即可得到点A到直线BD的距离，利用三角形的面积公式得到△ABD 的面积，再利用基本不等式的性质即可得出其最大值．解答：解：（Ⅰ）由题意可得，解得，∴椭圆C的方程为；（Ⅱ）设B（x1，y1），D（x2，y2）．由消去y得到，∵直线与椭圆有两个不同的交点，∴△=8﹣2m2＞0，解得﹣2＜m＜2．∴，．∴==．点A到直线BD的距离d==．∴===．当且仅当m=∈（﹣2，2）时取等号．∴当时，△ABD的面积取得最大值．点评：熟练掌握椭圆的定义、标准方程及其性质、直线与椭圆相交问题的解题模式、根与系数的关系、判别式、弦长公式、点到直线的距离公式、三角形的面积公式、基本不等式的性质是解题的关键．20．设m＞3，对于项数为m的有穷数列{a n}，令b k为a1，a2，a3…a k（k≤m）中的最大值，称数列{b n}为{a n}的“创新数列”．例如数列3，5，4，7的创新数列为3，5，5，7．考查自然数1、2…m（m＞3）的所有排列，将每种排列都视为一个有穷数列{c n}．（Ⅰ）若m=5，写出创新数列为3，5，5，5，5的所有数列{c n}；（Ⅱ）是否存在数列{c n}的创新数列为等比数列？若存在，求出符合条件的创新数列；若不存在，请说明理由；（Ⅲ）是否存在数列{c n}，使它的创新数列为等差数列？若存在，求出所有符合条件的数列{c n}的个数；若不存在，请说明理由．考点：等差数列与等比数列的综合．专题：新定义；等差数列与等比数列．分析：（I）由题意可得，创新数列为3，4，4，4的所有数列{c n}有两，即3，4，1，2和3，4，2，1．（II）设数列{c n}的创新数列为{e n}，因为e m为前m个自然数中最大的一个，所以e m=m，经检验，只有公比q=1时，数列{c n}才有唯一的一个创新数列．（III）设存在数列{c n}，使它的创新数列为等差数列，当d=0时，{e m}为常数列，满足条件；数列{c n}是首项为m的任意一个排列，共有个数列．当d=1时，符合条件的数列{e m}只能是1，2，3…m，此时数列{c n}是1，2，3…m，有1个．d≥2时，{e m} 不存在．由此得出结论．解答：解：（I）根据“创新数列”的定义，可得创新数列为3，5，5，5，5的数列{c n}有：3，5，1，2，4．3，5，1，4，2．3，5，2，1，4．3，5，2，4，1．3，5，4，1，2．3，5，4，2，1．…（4分）（II）存在数列{c n}的创新数列为等比数列．…（5分）设数列{c n}的创新数列为{e n}，因为e m为前m个自然数中最大的一个，所以e m=m．…（6分）若{e m}为等比数列，设公比为q，因为e k+1≥e k（k=1，2，3…m﹣1），所以q≥1．…（7分）当q=1时，{e m}为常数列满足条件，即为数列为常数数列，每一项都等于m．…（9分）当q＞1时，{e m}为增数列，符合条件的数列只能是1，2，3…m，又1，2，3…m不满足等比数列，综上符合条件的创新数列只有一个．…（10分）（3）设存在数列{c n}，使它的创新数列为等差数列，…（11分）设数列{c n}的创新数列为{e m}，因为e m为前m个自然数中最大的一个，所以e m=m．若{e m}为等差数列，设公差为d，因为e k+1≥e k（k=1，2，3…m﹣1），所以d≥0．且d∈N*．…（12分）当d=0时，{e m}为常数列，满足条件，即为数列e m=m，此时数列{c n}是首项为m的任意一个排列，共有个数列；…（14分）当d=1时，符合条件的数列{e m}只能是1，2，3…m，此时数列{c n}是1，2，3…m，有1个；…（15分）当d≥2时，∵e m=e1+（m﹣1）d≥e1+2（m﹣1）=e1+m+m﹣2 又m＞3，∴m﹣2＞0．∴e m＞m 这与e m=m矛盾，所以此时{e m} 不存在．…（17分）综上满足条件的数列{c n}的个数为（m﹣1）!+1个．…（18分）点评：本题主要考查等差关系的确定，等比关系的确定，创新数列的定义，属于中档题．。

2019-2020年高三下学期第二次模拟考试数学（理）试题含答案注意事项：1. 本试题分第I卷（选择题）和第II卷（非选择题）两部分.第I卷1至2页，第II卷3 至5页.满分150分，考试用时120分钟.2. 答卷前，考生务必将自己的姓名、学校、考生号涂写在答题卡上3. 第I卷共2页.答题时，考生须用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号.在试卷上作答无效.4. 第II卷写在答题卡对应的区域内，严禁在试题卷或草纸上答题.5. 考试结束后，只将答题卡交回. 参考公式：如果事件A,B相互独立，那么.第I卷（选择题共50分）一、选择题（本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有项是符合题目要求的.）1. 已知复数（i为虚数单位），则z在复平面内对应的点在A.第一象限B.第二象限C.第三象限D.第四象限2. 设集合A = <x x2—2x -3 £。

｝, B =｛y y =e x,x^ R｝，则A c B =A. B. C. D.3. 下列函数中，满足的单调递增函数是A. B.C. D.4. 已知两条不同的直线和两个不同的平面，有如下命题：①若丨l•上，m l.上，丨 / / ：, m / / ：,则：• / / ：；②若丨二-,l // '■二m,贝V l//m ；③若，其中正确命题的个数是A.3B.2C.1D.05. 函数的图象的大致形状是6. 利用简单随机抽样从某小区抽取100户居民进行月用电量调查，发现其用电量都在50到350 . 度之间，频率分布直方图如图所示.在这些用户:中，用电量落在区间［150 , 250］内的户数为A.46 C.50 D.52 7•已知直线与圆相交于 A,B 两点，且为等腰直角三角形，则实数 a 的值为A.B.C.D.18•将5名同学分成甲，乙，丙 3个小组，若甲组至少两人，乙、丙组至少各一人，则不同分组 方案的种数为 A.180B.120C.80D.609. 是各项不为零的等差数列，且公差，若删去此数列的某一项，得到的数列（按原来的顺序） 是等比数列，则的值为 A.1B.C.4D.uur uuu -10. 已知M 是内一点，且 AB ・AC =2.3「BAC =30°，若，的面积分别为则的最小值是A.16B.18C.19D.20第II 卷（非选择题共100分）二、填空题（本大题共5个小题，每小题 5分，共25分.）11. ____________________ 在中，若，则 12.已知双曲线的离心率为 2,它的一个焦点与抛物线的焦点相同，那么该双曲线的渐近线方B.48 程为 __________13.执行如图所示的程序框图， 若输入的，则输出的T 的值为 ____________14.记集合A = {(x,y 】(x _1 行 y 2 f},B=q]x,y )x _0 I ^<x 、2 y 色x1I '构成 的平面区域分别为 M,N ，现随机地向M 中抛一粒豆子（大小忽略不计）， 则该豆子落入N 中的概率为 ______________ . 15.已知函数f x = x^3ax 2 4,若f x 存在唯一的零点，则实数的取值范围是 _____________三、解答题（本大题共6小题，共75分.解答应写出必要的文字说明，证明过程或演算步骤 .） 16. （本小题满分12分）设的内角A,B,C 的对边分别是，已知. （I ）求角C 的大小；（II ） 如图，在的外角内取一点 P ，使PC=2,过点P 作于M ，于 N ， 设线段 PM ， PN 的长分别为nnm, n ，一 PCM 二x,且 x，求的最大值及相应 x 的值.6217. (本小题满分12分)如图，某快递公司送货员从公司A处准备开车送货到某单位B处，有A T C T B, A TF T B两条路线•若该地各路段发生堵车与否是相互独立的，且各路段发生堵车事件的概率如图所示(例如A T C T D算作两个路段；路段AC发生堵车事件的概率为，路段CD发生堵车事件的概率为)•(I)请你为其选择一条由A到B的路线，使得途中发生堵车事件的概率较小；(II)若记路线A T E T F T B中遇到堵车路段的个数为，求的分布列及其数学期望E().18. (本小题满分12分)如图，在四棱锥中，底面ABCD为直角梯形，AD//BC ,NADC =90°PA =PD =AD =2BC =2 ,, Q 是AD 的中点，M是棱PC上的点，且PM=3MC.(I)求证：平面底面ABCD ;(II)求二面角的大小.19. (本小题满分12分)已知数列的前n项和是且S n =2a n-n n・N” .(I)证明：数列是等比数列；(II)记，求数列的前n项和.20. (本小题满分13分)、，(1 已知函数f x 二a l x 2l n x, a • R .k x丿(I)当时，判断函数是否存在极值，若存在，求出极值；若不存在，说明理由;(II)求函数的单调区间.21. (本小题满分14分)已知椭圆E的中心在坐标原点O,它的长轴长，短轴长分别为，右焦点，直线轴相交于点, 过点A的直线m与椭圆E交于P, Q两点.(I)求椭圆E的方程；(II)若以线段PQ为直径的圆过原点O,求直线m的方程；(III )设，过点P且平行于直线I的直线与椭圆E相交于另一点M，求证：.2015年聊城市高考模拟试题文■理科数学（二）答案及评分标准大■銓10个小■•■小・5分•典50(1)C (2)A (3>A (4>C <S)B (5)D (7>C (8)C (9)B (10)&二.41空■:*大■貝5尔・.・小・$分•貝2S 分・11. ■詈 It 75x±j-O13.11S.(W )(-«.D<X>2三•■■■：*大■矣・个尔■•奚7S 分•■鲁"耳出文亨16.<a )(l7 t>(#^■■分M|< 1 )由•-ArotCH 余歿建Jie ta'・4i'+y-~・ip............................................. ... 2 分ffU AA W 三"于■手• .............................................................. 4 » < B W RfAPMl <p.PC-?.ZFMC-y.ZPCM-r.y<^<y>ffi U ■■ PC ・mx ・2・tLr ・ ...... ... ............ ........... . ... ................. ........ .......... .. .......... .. ........ ... 6 分 ft RtAPNC 中.PC7・"NC ・专•乙PCN ■号一*•U PC«n< — X )*2■氏芋■*)• ........................................... 。

2019-2020年高三下学期二模考试数学理(A )试题含答案■选择题：(5'X12=60‘)1•已知A= {x|x 羽k B= {x|<1},若AB 则实数k 的取值范围为()3.设f(x)是定义在R 上的奇函数，当 x 》0寸恒有f(x+2)=f(x)，当x €时, 2 26. a=b 是直线 y=x+2 与圆(x-a) +(y-b) =2 相切的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件7. 已知向量与的夹角为120 ° ||=3, |+|=，则||=()A.5B.4C.3D.18.设S n 为等差数列{ a n }的前n 项和，给出四个结论： (1) a 2+a 8^ a 2(2) S n =an +bn(a 丰 0)(3) 若 m,n,p,q € N +,贝V a m +a n =a p +a q 的充要条件是 m+n=p+q ⑷若 S 6=Sn ，贝V a 9=0其中正确命题的个数为( )一个交点的横坐标为 c ,则双曲线的离心率为A.+1B.+1C.+D.10.若 a>0,b>0 , lga+lgb=lg(a+b),则 a+b 的最小值为()A.8B.6C.4D.211. 若二项式()6的展开式中的常数项为 m ，则=()A. B.-C.D.-12. 定义在⑵在△ ABC 中，A 、B 、C 的对边为a 、b 、c , a= , S ^ABC =2 ,角C 为锐角且 f()=,求C 边长A.(1,+B.(- 8-1)C.(2,+ 8)D. f(x)=e x 1 ,则 f(xx)+f(-xx)=( ) C.-1-eD.e+1A.1-eB.e-14.在锐角三角形 ABC 中，BC=1 ,B=2A , 则的值为(A.6B.4C.2D.25.—个算法的程序框图如右图所示,若输入的x 值为xx ,则输出的值为( )A.3B.5C.6D.9A.1B.2C.3 9.已知双曲线-=1(a>0,b>0)的左、右焦点为 F 1(-c,0) , F 2(C ,0)，若直线 y=2x 与双曲线的18. 某同学参加语、数、外三门课程的考试，设该同学语、数、外取得优秀成绩的概率分别为,m, n(m>n)，设该同学三门课程都取得优秀成绩的概率为，都未取得优秀成绩的概率为, 且不同课程是否取得优秀成绩相互独立。