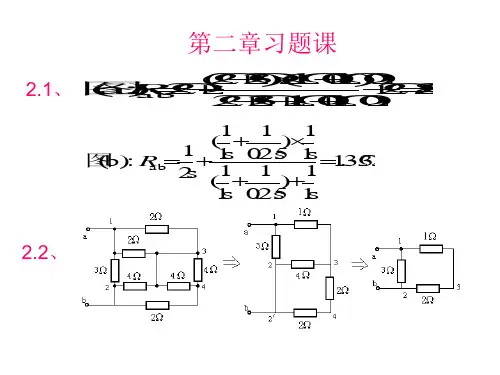
第二章习题选讲

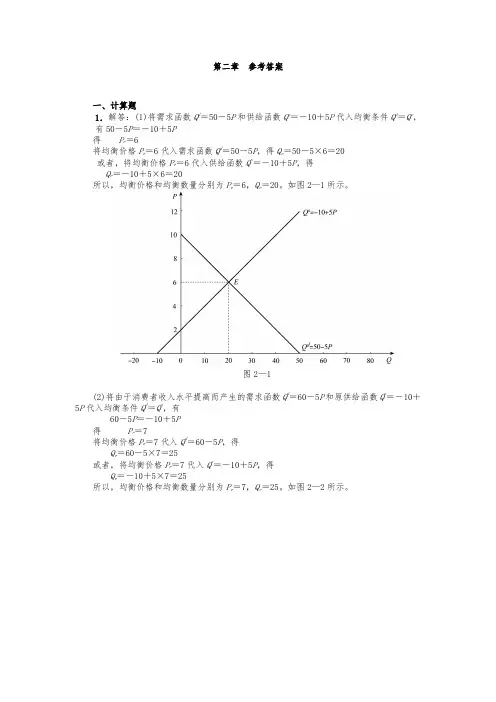
第二章参考答案一、计算题1．解答：(1)将需求函数Q d＝50－5P和供给函数Q s＝－10＋5P代入均衡条件Q d＝Q s，有50－5P＝－10＋5P得P e＝6将均衡价格P e＝6代入需求函数Q d＝50－5P，得Q e＝50－5×6＝20或者，将均衡价格P e＝6代入供给函数Q s＝－10＋5P，得Q e＝－10＋5×6＝20所以，均衡价格和均衡数量分别为P e＝6，Q e＝20。

如图2—1所示。

图2—1(2)将由于消费者收入水平提高而产生的需求函数Q d＝60－5P和原供给函数Q s＝－10＋5P代入均衡条件Q d＝Q s，有60－5P＝－10＋5P得P e＝7将均衡价格P e＝7代入Q d＝60－5P，得Q e＝60－5×7＝25或者，将均衡价格P e＝7代入Q s＝－10＋5P，得Q e＝－10＋5×7＝25所以，均衡价格和均衡数量分别为P e＝7，Q e＝25。

如图2—2所示。

图2—2(3)将原需求函数Q d＝50－5P和由于技术水平提高而产生的供给函数Q s＝－5＋5P代入均衡条件Q d＝Q s，有50－5P＝－5＋5P得P e＝5.5将均衡价格P e＝5.5代入Q d＝50－5P，得Q e＝50－5×5.5＝22.5或者，将均衡价格P e＝5.5代入Q s＝－5＋5P，得Q e＝－5＋5×5.5＝22.5所以，均衡价格和均衡数量分别为P e＝5.5，Q e＝22.5。

如图2—3所示。

图2—3(4)所谓静态分析是考察在既定条件下某一经济事物在经济变量的相互作用下所实现的均衡状态及其特征。

也可以说，静态分析是在一个经济模型中根据给定的外生变量来求内生变量的一种分析方法。

以(1)为例，在图2—1中，均衡点E就是一个体现了静态分析特征的点。

它是在给定的供求力量的相互作用下达到的一个均衡点。

在此，给定的供求力量分别用给定的供给函数Q s＝－10＋5P和需求函数Q d＝50－5P表示，均衡点E具有的特征是：均衡价格P e＝6，且当P e＝6时，有Q d＝Q s＝Q e＝20；同时，均衡数量Q e＝20，且当Q e＝20时，有P d＝P s＝P e＝6。

第2章习题课（二）习题课(二) 数列求和学习目标 1.掌握分组分解求和法的使用情形和解题要点.2.掌握奇偶并项求和法的使用情形和解题要点.3.掌握裂项相消求和法的使用情形和解题要点.4.进一步熟悉错位相减法． 知识点一 分组分解求和法思考 求和：112＋2122＋3123＋…＋⎝⎛⎭⎪⎪⎫n ＋12n . 答案 112＋2122＋3123＋…＋⎝ ⎛⎭⎪⎪⎫n ＋12n ＝(1＋2＋3＋…＋n )＋⎝⎛⎭⎪⎪⎫12＋122＋123＋ (12)＝n (n ＋1)2＋12⎝ ⎛⎭⎪⎪⎫1－12n 1－12＝n (n ＋1)2＋1－12n .梳理 分组分解求和的基本思路：通过分解每一项重新组合，化归为等差数列和等比数列求和．答案 由1n (n ＋1)＝1n －1n ＋1，得11×2＋12×3＋…＋1n (n ＋1)＝1－12＋12－13＋…＋1n －1(n ＋1)＝1－1n ＋1.梳理 如果数列的项能裂成前后抵消的两项，则可用裂项相消法求和，此法一般先研究通项的形式，然后仿照公式裂开每一项．裂项相消求和常用公式：(1)1n (n ＋k )＝1k ⎝⎛⎭⎪⎪⎫1n －1n ＋k ； (2)1n ＋k ＋n ＝1k (n ＋k －n )；(3)1(2n －1)(2n ＋1)＝12⎝ ⎛⎭⎪⎪⎫12n －1－12n ＋1；(4)1n (n ＋1)(n ＋2)＝12⎣⎢⎢⎡⎦⎥⎥⎤1n (n ＋1)－1(n ＋1)(n ＋2). 1．并项求和一定是相邻两项结合．(×) 2．裂项相消一定是相邻两项裂项后产生抵消．(×)类型一 分组分解求和例1 求和：S n ＝⎝⎛⎭⎪⎪⎫x ＋1x 2＋⎝ ⎛⎭⎪⎪⎫x 2＋1x 22＋…＋⎝ ⎛⎭⎪⎪⎫x n ＋1x n 2(x ≠0)．考点 数列前n 项和的求法 题点 分组求和法 解 当x ≠±1时，S n ＝⎝⎛⎭⎪⎪⎫x ＋1x 2＋⎝ ⎛⎭⎪⎪⎫x 2＋1x 22＋…＋⎝⎛⎭⎪⎪⎫x n ＋1x n 2 ＝⎝⎛⎭⎪⎪⎫x 2＋2＋1x 2＋⎝ ⎛⎭⎪⎪⎫x 4＋2＋1x 4＋…＋⎝⎛⎭⎪⎪⎫x 2n ＋2＋1x 2n ＝(x 2＋x 4＋…＋x 2n )＋2n ＋⎝⎛⎭⎪⎪⎫1x 2＋1x 4＋…＋1x 2n＝x 2(x 2n －1)x 2－1＋x －2(1－x －2n )1－x －2＋2n ＝(x 2n －1)(x 2n ＋2＋1)x 2n(x 2－1)＋2n ； 当x ＝±1时，S n ＝4n . 综上知，S n ＝⎩⎪⎨⎪⎧4n ，x ＝±1，(x 2n －1)(x 2n ＋2＋1)x 2n (x 2－1)＋2n ，x ≠±1且x ≠0.反思与感悟 某些数列，通过适当分组，可得出两个或几个等差数列或等比数列，进而利用等差数列或等比数列的求和公式分别求和，从而得出原数列的和．跟踪训练1 求数列1,1＋a,1＋a ＋a 2，…，1＋a ＋a 2＋…＋an －1，…的前n 项和S n .(其中a ≠0，n ∈N *)考点 数列前n 项和的求法 题点 分组求和法 解 当a ＝1时，a n ＝n ，于是S n ＝1＋2＋3＋…＋n ＝n (n ＋1)2.当a ≠1时，a n ＝1－a n 1－a ＝11－a (1－a n )．∴S n ＝11－a[n －(a ＋a 2＋…＋a n )]＝11－a ⎣⎢⎢⎡⎦⎥⎥⎤n －a (1－a n )1－a ＝n 1－a －a (1－a n )(1－a )2. ∴S n ＝⎩⎪⎪⎨⎪⎪⎧n (n ＋1)2，a ＝1，n 1－a －a (1－a n)(1－a )2，a ≠1，且a ≠0.类型二 裂项相消求和例2 求和：122－1＋132－1＋142－1＋…＋1n 2－1，n ≥2， n ∈N *.考点 数列前n 项和的求法 题点 裂项相消法求和解 ∵1n 2－1＝1(n －1)(n ＋1)＝12⎝ ⎛⎭⎪⎪⎫1n －1－1n ＋1， ∴原式＝12⎣⎢⎢⎡⎝⎛⎭⎪⎪⎫1－13＋⎝ ⎛⎭⎪⎪⎫12－14＋⎝ ⎛⎭⎪⎪⎫13－15⎦⎥⎥⎤＋…＋⎝ ⎛⎭⎪⎪⎫1n －1－1n ＋1＝12⎝ ⎛⎭⎪⎪⎫1＋12－1n －1n ＋1 ＝34－2n ＋12n (n ＋1)(n ≥2，n ∈N *)． 引申探究求和：2222－1＋3232－1＋4242－1＋…＋n 2n 2－1，n ≥2，n ∈N *.解 ∵n 2n 2－1＝n 2－1＋1n 2－1＝1＋1n 2－1，∴原式＝⎝ ⎛⎭⎪⎪⎫1＋122－1＋⎝ ⎛⎭⎪⎪⎫1＋132－1＋⎝ ⎛⎭⎪⎪⎫1＋142－1＋…＋⎝⎛⎭⎪⎪⎫1＋1n 2－1 ＝(n －1)＋⎝ ⎛⎭⎪⎪⎫122－1＋132－1＋142－1＋…＋1n 2－1 以下同例2解法．反思与感悟 求和前一般先对数列的通项公式变形，如果数列的通项公式可转化为f (n ＋1)－f (n )的形式，常采用裂项求和法． 跟踪训练2 求和：1＋11＋2＋11＋2＋3＋…＋11＋2＋3＋…＋n ，n ∈N *.考点 数列前n 项和的求法题点 裂项相消法求和 解∵a n＝11＋2＋…＋n ＝2n (n ＋1)＝2⎝⎛⎭⎪⎪⎫1n －1n ＋1， ∴S n ＝2⎝ ⎛⎭⎪⎪⎫1－12＋12－13＋…＋1n －1n ＋1＝2n n ＋1. 类型三 奇偶并项求和例3 求和：S n ＝－1＋3－5＋7－…＋(－1)n (2n －1)．考点 数列前n 项和的求法 题点 并项求和法 解 当n 为奇数时，S n ＝(－1＋3)＋(－5＋7)＋(－9＋11)＋… ＋[(－2n ＋5)＋(2n －3)]＋(－2n ＋1) ＝2·n －12＋(－2n ＋1)＝－n .当n为偶数时，S n＝(－1＋3)＋(－5＋7)＋…＋[(－2n＋3)＋(2n ＝n.－1)]＝2·n2∴S n＝(－1)n n (n∈N*)．反思与感悟通项中含有(－1)n的数列求前n项和时可以考虑使用奇偶并项法，分项数为奇数和偶数分别进行求和．跟踪训练3已知数列－1,4，－7,10，…，(－1)n·(3n－2)，…，求其前n项和S n.考点数列前n项和的求法题点并项求和法解当n为偶数时，令n＝2k(k∈N*)，S n＝S2k＝－1＋4－7＋10＋…＋(－1)n·(3n－2) ＝(－1＋4)＋(－7＋10)＋…＋[(－6k＋5)＋(6k－2)] ＝3k ＝32n ；当n 为奇数时， 令n ＝2k ＋1(k ∈N *)，S n ＝S 2k ＋1＝S 2k ＋a 2k ＋1＝3k －(6k ＋1)＝－3n ＋12.∴S n ＝⎩⎪⎨⎪⎧－3n ＋12，n 为奇数，3n 2，n 为偶数.1．数列{1＋2n －1}的前n 项和为________．考点 数列前n 项和的求法 题点 分组求和法答案 S n ＝n ＋2n －1，n ∈N * 解析 ∵a n ＝1＋2n －1， ∴S n ＝n ＋1－2n1－2＝n ＋2n －1.2．已知数列a n ＝⎩⎨⎧n －1，n 为奇数，n ，n 为偶数，则S 100＝________.考点 数列前n 项和的求法 题点 分组求和法 答案 5 000解析 由题意得S 100＝a 1＋a 2＋…＋a 99＋a 100 ＝(a 1＋a 3＋a 5＋…＋a 99)＋(a 2＋a 4＋…＋a 100) ＝(0＋2＋4＋…＋98)＋(2＋4＋6＋…＋100) ＝5 000.3．已知a n ＝(－1)n ，数列{a n }的前n 项和为S n ，则S 9与S 10的值分别是________． 考点 数列前n 项和的求法 题点 并项求和法 答案 －1,0解析 S 10＝(a 1＋a 2)＋(a 3＋a 4)＋…＋(a 9＋a 10)＝0，S 9＝S 10－a 10＝－1.4．求数列112＋2，122＋4，132＋6，142＋8，…的前n 项和．考点 数列前n 项和的求法 题点 裂项相消法求和解 因为通项a n ＝1n 2＋2n ＝12⎝ ⎛⎭⎪⎪⎫1n －1n ＋2， 所以此数列的前n 项和S n ＝12⎣⎢⎢⎡⎝ ⎛⎭⎪⎪⎫1－13＋⎝ ⎛⎭⎪⎪⎫12－14＋⎝ ⎛⎭⎪⎪⎫13－15⎦⎥⎥⎤＋…＋⎝ ⎛⎭⎪⎪⎫1n －1－1n ＋1＋⎝⎛⎭⎪⎪⎫1n －1n ＋2 ＝12⎝ ⎛⎭⎪⎪⎫1＋12－1n ＋1－1n ＋2＝34－2n ＋32(n ＋1)(n ＋2). 求数列的前n 项和，一般有下列几种方法． 1．错位相减适用于一个等差数列和一个等比数列对应项相乘构成的数列求和． 2．分组求和把一个数列分成几个可以直接求和的数列． 3．裂项相消把一个数列的通项公式分成两项差的形式，相加过程消去中间项，只剩有限项再求和． 4．奇偶并项当数列通项中出现(－1)n 或(－1)n ＋1时，常常需要对n 取值的奇偶性进行分类讨论．5．倒序相加例如，等差数列前n 项和公式的推导方法． 一、填空题1．数列{a n }的前n 项和为S n ，若a n ＝1n (n ＋1)， 则S 5＝______.考点 数列前n 项和的求法 题点 裂项相消法求和 答案 56解析 ∵a n ＝1n (n ＋1)＝1n －1n ＋1.∴S 5＝⎝⎛⎭⎪⎪⎫1－12＋⎝ ⎛⎭⎪⎪⎫12－13＋…＋⎝ ⎛⎭⎪⎪⎫15－16 ＝1－16＝56.2．在等比数列{a n }中，若a 1＝12，a 4＝－4，则|a 1|＋|a 2|＋|a 3|＋…＋|a n |＝________. 考点 数列前n 项和的求法题点 数列求和方法综合 答案 2n －12解析 ∵{a n }为等比数列，且a 1＝12，a 4＝－4，∴q 3＝a 4a 1＝－8，∴q ＝－2，∴a n ＝12(－2)n －1，∴|a n |＝2n －2，∴|a 1|＋|a 2|＋|a 3|＋…＋|a n |＝12(1－2n )1－2＝2n －12.3．已知数列{a n }的通项a n ＝2n ＋1，n ∈N *，由b n ＝a 1＋a 2＋a 3＋…＋a nn 所确定的数列{b n }的前n 项和是__________． 考点 数列前n 项和的求法 题点 数列求和方法综合 答案 12n (n ＋5)解析 ∵a 1＋a 2＋…＋a n ＝n2(2n ＋4)＝n 2＋2n ，∴b n ＝n ＋2，∴{b n }的前n 项和S n ＝n (n ＋5)2.4．在数列{a n }中，已知S n ＝1－5＋9－13＋17－21＋…＋(－1)n －1(4n －3)，n ∈N *，则S 15＋S 22－S 31的值是________． 考点 数列前n 项和的求法 题点 并项求和法 答案 －76解析 S 15＝－4×7＋a 15＝－28＋57＝29， S 22＝－4×11＝－44，S 31＝－4×15＋a 31＝－60＋121＝61， S 15＋S 22－S 31＝29－44－61＝－76.5．如果一个数列{a n }满足a n ＋a n ＋1＝H (H 为常数，n ∈N *)，则称数列{a n }为等和数列，H 为公和，S n 是其前n 项的和，已知在等和数列{a n }中，a1＝1，H＝－3，则S2 017＝________.考点数列前n项和的求法题点并项求和法答案－3 023解析S2 017＝a1＋(a2＋a3＋…＋a2 017)＝a1＋1 008×H＝1＋1 008×(－3)＝－3 023.6．数列{a n}的通项公式是a n＝1n＋n＋1，若前n项和为10，则n的值为________．考点数列前n项和的求法题点裂项相消法求和答案120解析∵a n＝1n＋n＋1＝n＋1－n，∴S n＝a1＋a2＋…＋a n＝(2－1)＋(3－2)＋…＋(n＋1－n)＝n ＋1－1，令n ＋1－1＝10，得n ＝120.7．数列1,1＋2,1＋2＋22，...，1＋2＋22＋ (2)－1，…的前99项和为________．考点 数列前n 项和的求法 题点 并项求和法 答案 2100－101解析 由数列可知a n ＝1＋2＋22＋…＋2n －1＝1－2n1－2＝2n －1，所以，前99项的和为S 99＝(2－1)＋(22－1)＋…＋(299－1)＝2＋22＋…＋299－99＝2(1－299)1－2－99＝2100－101.8．若S n ＝1－2＋3－4＋…＋(－1)n －1·n ，n ∈N *，则S 50＝________.考点 数列前n 项和的求法题点 并项求和法 答案 －25解析 S 50＝1－2＋3－4＋…＋49－50＝(－1)×25＝－25.9．在数列{a n }中，若a n ＝ln ⎝⎛⎭⎪⎪⎫1＋1n ，n ∈N *，则S n ＝______.考点 数列前n 项和的求法 题点 裂项相消法求和 答案 ln(n ＋1)解析 方法一 a n ＝ln n ＋1n ＝ln(n ＋1)－ln n S n ＝(ln 2－ln 1)＋(ln 3－ln 2)＋…＋[ln(n ＋1)－ln n ]＝ln(n ＋1)－ln 1＝ln(n ＋1)．方法二 S n ＝ln 21＋ln 32＋…＋ln n ＋1n＝ln ⎝ ⎛⎭⎪⎫21×32×…×n ＋1n ＝ln(n ＋1)．10．数列12×5，15×8，18×11，…，1(3n －1)×(3n ＋2)，…的前n 项和为__________．考点 数列前n 项和的求法 题点 裂项相消法求和 答案 n6n ＋4解析 由数列通项公式1(3n －1)(3n ＋2)＝13⎝ ⎛⎭⎪⎪⎫13n －1－13n ＋2， 得前n 项和S n＝13⎝ ⎛⎭⎪⎪⎫12－15＋15－18＋18－111＋…＋13n －1－13n ＋2 ＝13⎝ ⎛⎭⎪⎪⎫12－13n ＋2＝n 6n ＋4. 11．数列{a n }的通项公式a n ＝n cos n π2，n ∈N *，其前n 项和为S n ，则S 2 016＝________.题点并项求和法答案 1 008解析a1＝cos π2＝0，a2＝2cos π＝－2，a3＝0，a4＝4，….∴数列{a n}的所有奇数项为0，前2 016项的所有偶数项(共1 008项)依次为－2,4，－6,8，…，故S2 016＝0＋(－2＋4)＋(－6＋8)＋…＋(－2 014＋2 016)＝1 008.二、解答题12．已知等差数列{a n}满足：a3＝7，a5＋a7＝26，{a n}的前n项和为S n.(1)求a n及S n；(2)令b n＝1a2n－1(n∈N*)，求数列{b n}的前n项和T n.题点 裂项相消法求和解 (1)设等差数列{a n }的首项为a 1，公差为d .因为a 3＝7，a 5＋a 7＝26，所以⎩⎨⎧a 1＋2d ＝7，2a 1＋10d ＝26，解得⎩⎨⎧a 1＝3，d ＝2.所以a n ＝3＋2(n －1)＝2n ＋1， S n ＝3n ＋n (n －1)2×2＝n 2＋2n .所以a n ＝2n ＋1，S n ＝n 2＋2n . (2)由(1)知a n ＝2n ＋1，所以b n ＝1a 2n －1＝1(2n ＋1)2－1＝14×1n (n ＋1)＝14×⎝ ⎛⎭⎪⎪⎫1n －1n ＋1，所以T n ＝14×⎝ ⎛⎭⎪⎪⎫1－12＋12－13＋…＋1n －1n ＋1 ＝14×⎝ ⎛⎭⎪⎪⎫1－1n ＋1＝n 4(n ＋1)， 即数列{b n }的前n 项和T n ＝n 4(n ＋1).13．设数列{a n }满足a 1＝2，a n ＋1－a n ＝3·22n －1，n ∈N *.(1)求数列{a n }的通项公式；(2)令b n ＝na n ，求数列{b n }的前n 项和S n . 考点 数列前n 项和的求法 题点 错位相减法求和 解 (1)由已知，得当n >1时，a n ＝[(a n －a n －1)＋(a n －1－a n －2)＋…＋(a 2－a 1)]＋a 1＝3(22n －3＋22n －5＋…＋2)＋2＝22n －1， 而a 1＝2，符合上式，所以数列{a n }的通项公式为a n ＝22n －1. (2)由b n ＝na n ＝n ·22n －1知S n ＝1·2＋2·23＋3·25＋…＋n ·22n －1， ① 从而22·S n ＝1·23＋2·25＋3·27＋…＋n ·22n ＋1. ② ①－②得(1－22)S n ＝2＋23＋25＋…＋22n －1－n ·22n ＋1， 即S n ＝19[(3n －1)22n ＋1＋2]．三、探究与拓展14．设数列{a n }满足a 1＝0且11－a n ＋1－11－a n ＝1，n ∈N *.(1)求{a n }的通项公式；(2)设b n ＝1－a n ＋1n ，记S n ＝b 1＋b 2＋…＋b n ，证明：S n <1.考点 数列前n 项和的求法题点 裂项相消法求和(1)解 由题设11－a n ＋1－11－a n ＝1知，⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫11－a n 是公差为1的等差数列， 又11－a 1＝1，故11－a n ＝n ， ∴a n ＝1－1n .(2)证明 由(1)得b n ＝1－a n ＋1n ＝n ＋1－nn ＋1·n＝1n －1n ＋1，∴S n ＝1－12＋12－13＋13－14＋…＋1n －1n ＋1＝1－1n ＋1<1.15．已知在数列{a n }中，a 1＝1，a n ·a n ＋1＝⎝⎛⎭⎪⎪⎫12n，记T 2n 为{a n }的前2n 项的和，b n ＝a 2n ＋a 2n －1，n ∈N *. (1)判断数列{b n }是否为等比数列，并求出{b n }； (2)求T 2n .考点 数列前n 项和的求法 题点 分组求和法 解 (1)因为a n ·a n ＋1＝⎝⎛⎭⎪⎪⎫12n，所以a n ＋1·a n ＋2＝⎝⎛⎭⎪⎪⎫12n ＋1， 所以a n ＋2a n ＝12，即a n ＋2＝12a n ，因为b n ＝a 2n ＋a 2n －1， 所以b n ＋1b n ＝a 2n ＋2＋a 2n ＋1a 2n ＋a 2n －1＝12a 2n ＋12a 2n －1a 2n ＋a 2n －1＝12，所以{b n }是公比为12的等比数列．因为a 1＝1，a 1·a 2＝12，所以a 2＝12，所以b 1＝a 1＋a 2＝32，所以b n ＝32×⎝ ⎛⎭⎪⎪⎫12n －1＝32n .(2)由(1)可知a n ＋2＝12a n ，所以a 1，a 3，a 5，…是以a 1＝1为首项，12为公比的等比数列；a 2，a 4，a 6，…是以a 2＝12为首项，12为公比的等比数列，所以T 2n ＝(a 1＋a 3＋…＋a 2n －1)＋(a 2＋a 4＋…＋a 2n )＝1－⎝⎛⎭⎪⎪⎫12n1－12＋12⎣⎢⎢⎡⎦⎥⎥⎤1－⎝ ⎛⎭⎪⎪⎫12n 1－12＝3－32n .。

宏观经济学第二章习题及答案第二单元产品市场中国民收入的决定本单元所涉及到的主要知识点：1．国民收入均衡条件：意愿I=S；2．消费函数、储蓄函数、税收函数、政府购买函数与净出口函数；3．国民收入的决定；4．国民收入的变动：乘数理论。

一、单项选择1．凯恩斯在《通论》中指出( D )。

a．宏观均衡与大量失业并不矛盾；b．工资和价格对市场上的非均衡不能及时作出反映；c．管理总需求的干预政策能影响产出和就业；d．以上均是。

2．与凯恩斯观点不同,古典宏观经济学家认为(D )。

a．工资和价格总是对非均衡及时作出反应；b．失业要么是自愿的,要么是由于工资调整的人为障碍引起的；c．总供给曲线在潜在GDP处是垂直的；d．以上均是。

3．如果消费增加即消费曲线向上移动,这意味着消费者(D )。

a．由于减少收入而减少储蓄；b．由于增加收入而增加了储蓄；c．不是由于增加收入而是其他原因使储蓄增加；d．不是由于增加收入而是其他原因使储蓄减少。

4．在两部门经济中,收入在( C )时均衡下来。

a．储蓄等于实际投资； b．消费等于实际投资；c．储蓄等于计划投资； d．消费等于计划投资。

5．消费函数C=C0+cY d (C0>0,0<c<1)表明,平均消费倾向( A )。

a．大于边际消费倾向； b．小于边际消费倾向；c．等于边际消费倾向； d．以上三种情况都可能。

6．储蓄函数S=S0+sY d(S0<0,0<s<1)表明，平均储蓄倾向随着可支配收入的增加（ B ）。

a．递减； b．递增； c．不变； d．先递减然后递增。

7．凯恩斯之前的古典理论认为（ D ）。

a．储蓄是收入的函数，而投资是利率的函数；b．储蓄和投资都是收入的函数；c．投资取决于收入，而储蓄取决于利率；d．储蓄和投资都是利率的函数。

8．总产出固定并且国民储蓄与利息率无关时，税收的增加将（ D ）a．使垂真的储蓄曲线向左移动； b．减少投资；c．增加消费； d．减少均衡利率并增加投资。