LZW 编码详解

LZW编码算法详解LZW(Lempel-Ziv & Welch)编码又称字串表编码，是Welch将Lemple和Ziv所提出来的无损压缩技术改进后的压缩方法。

GIF图像文件采用的是一种改良的LZW 压缩算法，通常称为GIF-LZW压缩算法。

下面简要介绍GIF-LZW的编码与解码方程解：例现有来源于二色系统的图像数据源（假设数据以字符串表示）：aabbbaabb，试对其进行LZW编码及解码。

1）根据图像中使用的颜色数初始化一个字串表（如表1），字串表中的每个颜色对应一个索引。

在初始字串表的LZW_CLEAR和LZW_EOI分别为字串表初始化标志和编码结束标志。

设置字符串变量S1、S2并初始化为空。

2）输出LZW_CLEAR在字串表中的索引3H(见表2第一行)。

3）从图像数据流中第一个字符开始，读取一个字符a，将其赋给字符串变量S2。

判断S1+S2=“a”在字符表中，则S1=S1+S2=“a”（见表2第二行）。

4）读取图像数据流中下一个字符a，将其赋给字符串变量S2。

判断S1+S2=“aa”不在字符串表中，输出S1=“a”在字串表中的索引0H，并在字串表末尾为S1+S2="aa"添加索引4H，且S1=S2=“a”（见表2第三行）。

5）读下一个字符b赋给S2。

判断S1+S2=“ab”不在字符串表中，输出S1=“a”在字串表中的索引0H，并在字串表末尾为S1+S2=“ab”添加索引5H，且S1=S2=“b”（见表2第四行）。

6）读下一个字符b赋给S2。

S1+S2=“bb”不在字串表中，输出S1=“b”在字串表中的索引1H，并在字串表末尾为S1+S2=“bb”添加索引6H，且S1=S2=“b”（见表2第五行）。

7）读字符b赋给S2。

S1+S2=“bb”在字串表中，则S1=S1+S2=“bb”（见表2第六行）。

8）读字符a赋给S2。

S1+S2=“bba”不在字串表中，输出S1=“bb”在字串表中的索引6H，并在字串表末尾为S1+S2=“bba”添加索引7H，且S1=S2=“a”（见表2第七行）。

C语言数据压缩哈夫曼编码和LZW算法C语言数据压缩——哈夫曼编码与LZW算法在计算机科学中，数据压缩是一种重要的技术，它可以有效地减少数据的存储空间和传输带宽。

本文将介绍两种常用的数据压缩算法，分别是哈夫曼编码和LZW算法，并给出它们在C语言中的实现方法。

一、哈夫曼编码1. 哈夫曼编码的原理哈夫曼编码是一种前缀编码方法，它根据字符出现的频率构建一棵表示编码的二叉树，频率越高的字符离根节点越近。

通过将二叉树的左、右分支分别标记为0和1，可以得到每个字符的唯一编码。

2. 实现哈夫曼编码的步骤（1）统计字符频率：遍历待压缩的数据，统计每个字符出现的频率。

（2）构建哈夫曼树：根据字符频率构建哈夫曼树，使用优先队列或堆来实现。

（3）生成哈夫曼编码表：通过遍历哈夫曼树，从根节点到各个叶子节点的路径上的0、1序列构建编码表。

（4）进行编码：根据生成的哈夫曼编码表，将待压缩数据转换为对应的编码。

（5）进行解码：利用哈夫曼树和生成的哈夫曼编码表，将编码解析为原始数据。

二、LZW算法1. LZW算法的原理LZW算法是一种字典压缩算法，它不需要事先进行字符频率统计，而是根据输入数据动态构建一个字典。

将输入数据中的序列与字典中的条目逐一匹配，若匹配成功则继续匹配下一个字符，若匹配失败则将当前序列加入字典，并输出该序列的编码。

2. 实现LZW算法的步骤（1）初始化字典：将所有可能的单字符作为字典的初始条目。

（2）读入输入数据：依次读入待压缩的数据。

（3）匹配字典：将读入的字符与字典中的条目逐一匹配，直到无法匹配成功。

（4）输出编码：将匹配成功的条目对应的编码输出。

（5）更新字典：若匹配失败，则将当前序列添加到字典中，并输出前一个匹配成功的条目对应的编码。

（6）重复步骤（3）至（5），直到输入数据全部处理完毕。

三、C语言实现1. 哈夫曼编码的C语言实现```c// TODO：哈夫曼编码的C语言实现```2. LZW算法的C语言实现```c// TODO：LZW算法的C语言实现```四、总结本文介绍了C语言中两种常用的数据压缩算法——哈夫曼编码和LZW算法。

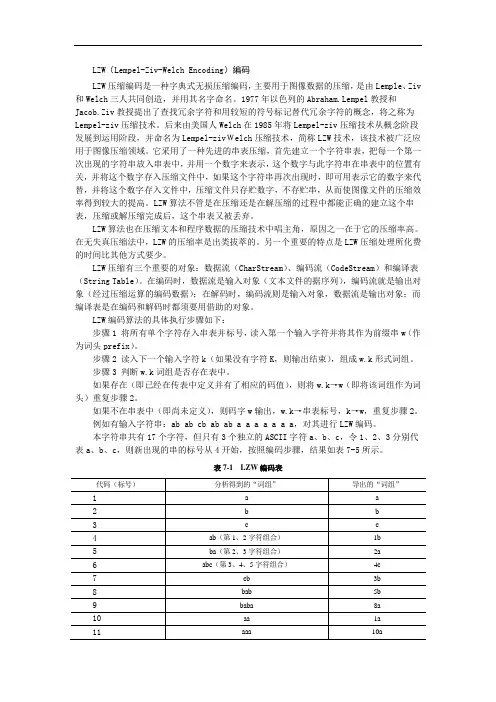
LZW（Lempel-Ziv-Welch Encoding）编码LZW压缩编码是一种字典式无损压缩编码，主要用于图像数据的压缩，是由Lemple、Ziv 和Welch三人共同创造，并用其名字命名。

1977年以色列的Abraham.Lempel教授和Jacob.Ziv教授提出了查找冗余字符和用较短的符号标记替代冗余字符的概念，将之称为Lempel-ziv压缩技术。

后来由美国人Welch在1985年将Lempel-ziv压缩技术从概念阶段发展到运用阶段，并命名为Lempel-zivＷelch压缩技术，简称LZW技术，该技术被广泛应用于图像压缩领域。

它采用了一种先进的串表压缩，首先建立一个字符串表，把每一个第一次出现的字符串放入串表中，并用一个数字来表示，这个数字与此字符串在串表中的位置有关，并将这个数字存入压缩文件中，如果这个字符串再次出现时，即可用表示它的数字来代替，并将这个数字存入文件中，压缩文件只存贮数字，不存贮串，从而使图像文件的压缩效率得到较大的提高。

LZW算法不管是在压缩还是在解压缩的过程中都能正确的建立这个串表，压缩或解压缩完成后，这个串表又被丢弃。

LZW算法也在压缩文本和程序数据的压缩技术中唱主角，原因之一在于它的压缩率高。

在无失真压缩法中，LZW的压缩率是出类拔萃的。

另一个重要的特点是LZW压缩处理所化费的时间比其他方式要少。

LZW压缩有三个重要的对象：数据流（CharStream）、编码流（CodeStream）和编译表（String Table）。

在编码时，数据流是输入对象（文本文件的据序列），编码流就是输出对象（经过压缩运算的编码数据）；在解码时，编码流则是输入对象，数据流是输出对象；而编译表是在编码和解码时都须要用借助的对象。

LZW编码算法的具体执行步骤如下：步骤1 将所有单个字符存入串表并标号，读入第一个输入字符并将其作为前缀串w（作为词头prefix）。

步骤2 读入下一个输入字符k（如果没有字符K，则输出结束），组成w.k形式词组。

LZW（Lempel-Ziv-Welch）是一种无损数据压缩算法。

以下是一个简单的C语言实现的LZW编码和解码示例：```c#include <stdio.h>#include <stdlib.h>#include <string.h>#define MAX_CODE_SIZE 128typedef struct {int code;char ch;} Code;void init_codes(Code codes[]) {for (int i = 0; i < MAX_CODE_SIZE; i++) {codes[i].code = i;codes[i].ch = i;}}int next_code(Code codes[], char ch) {for (int i = 0; i < MAX_CODE_SIZE; i++) {if (codes[i].ch == ch) {return codes[i].code;}}return -1;}void compress(char *input, char *output) {Code codes[MAX_CODE_SIZE];init_codes(codes);int input_len = strlen(input);int output_index = 0;int current_code = 256;int current_len = 1;int max_len = 1;int next_index = 0;output[output_index++] = codes[current_code].ch;for (int i = 1; i < input_len; i++) {next_index = next_code(codes, input[i]);current_len++;if (next_index != -1) {current_code = next_index;} else {current_code = codes[current_code].code;codes[current_code].ch = input[i];current_code++;current_len = 1;}if (current_len > max_len) {max_len = current_len;}if (current_len == max_len && current_code < MAX_CODE_SIZE) { output[output_index++] = codes[current_code].ch;current_code++;current_len = 0;max_len = 1;}}output[output_index] = '\0';}void decompress(char *input, char *output) {Code codes[MAX_CODE_SIZE];init_codes(codes);int input_len = strlen(input);int output_index = 0;int current_code = 0;int current_len = 0;int max_len = 0;int next_index = 0;while (input[current_code] != '\0') {current_len++;next_index = next_code(codes, input[current_code]);if (next_index != -1) {current_code = next_index;} else {codes[current_code].ch = input[current_code];current_code++;current_len = 1;}if (current_len > max_len) {max_len = current_len;}if (current_len == max_len && current_code < MAX_CODE_SIZE) {output[output_index++] = codes[current_code].ch;current_code++;current_len = 0;max_len = 0;}}output[output_index] = '\0';}int main() {char input[] = "ABABABABA";char output[256];compress(input, output);printf("Compressed: %s", output);char decompressed[256];decompress(output, decompressed);printf("Decompressed: %s", decompressed);return 0;}```这个示例中，`init_codes`函数用于初始化编码表，`next_code`函数用于查找下一个编码，`compress`函数用于压缩输入字符串，`decompress`函数用于解压缩输出字符串。

lzw编码原理
LZW（Lempel-Ziv-Welch）编码是一种无损压缩算法，基于字典的压缩算法。

它的原理如下：
1. 初始化字典：创建一个初始字典，其中包含所有单个输入符号（字符）作为键，对应的编码为它们的ASCII码值。

2. 分割输入：将输入字符串分割为一个个输入符号的序列。

3. 初始化缓冲区：将第一个输入符号加入到缓冲区中。

4. 处理输入序列：从第二个输入符号开始，重复以下步骤直到处理完所有输入符号：
- 将当前输入符号与缓冲区中的符号连接，得到一个新的符号。

- 如果新的符号在字典中存在，则将其加入到缓冲区中，继续处理下一个输入符号。

- 如果新的符号不在字典中，则将缓冲区中的符号编码输出，将新的符号添加到字典中，并将新的符号作为下一个缓冲区。

5. 输出编码：当所有输入符号处理完后，将缓冲区中的符号（不包括最后一个输入符号）编码输出。

LZW编码的核心思想是使用字典记录出现过的符号及其编码，以减少编码的长度。

在处理输入序列时，如果新的符号在字典中存在，则将其添加到缓冲区，并继续处理下一个输入符号；如果新的符号不在字典中，则将缓冲区中的符号编码输出，并将新的符号添加到字典中。

由于LZW编码使用了字典记录已编码的符号，因此在解码时只需根据字典中的编码逆向查找对应的符号即可恢复原始输入序列。

实验2 用C语言实现LZW编码1.实验目的1)通过实验进一步掌握LZW编码的原理2)能正确C语言实现LZW编、解码2.实验要求给出字符，能正确输出编码，并能进行译码3.实验内容1)编码过程LZW编码是围绕称为词典的转换表来完成的。

这张转换表用来存放称为前缀(Prefix)的字符序列，并且为每个表项分配一个码字(Code word)，或者叫做序号，如表6所示。

这张转换表实际上是把8位ASCII字符集进行扩充，增加的符号用来表示在文本或图像中出现的可变长度ASCII字符串。

扩充后的代码可用9位、10位、11位、12位甚至更多的位来表示。

Welch的论文中用了12位，12位可以有4096个不同的12位代码，这就是说，转换表有4096个表项，其中256个表项用来存放已定义的字符，剩下3840个表项用来存放前缀(Prefix)。

表6 词典LZW编码器(软件编码器或硬件编码器)就是通过管理这个词典完成输入与输出之间的转换。

LZW编码器的输入是字符流(Charstream)，字符流可以是用8位ASCII字符组成的字符串，而输出是用n位(例如12位)表示的码字流(Codestream)，码字代表单个字符或多个字符组成的字符串。

LZW编码器使用了一种很实用的分析(parsing)算法，称为贪婪分析算法(greedy parsing algorithm)。

在贪婪分析算法中，每一次分析都要串行地检查来自字符流(Charstream)的字符串，从中分解出已经识别的最长的字符串，也就是已经在词典中出现的最长的前缀(Prefix)。

用已知的前缀(Prefix)加上下一个输入字符C也就是当前字符(Current character)作为该前缀的扩展字符，形成新的扩展字符串——缀-符串(String)：Prefix.C。

这个新的缀-符串(String)是否要加到词典中，还要看词典中是否存有和它相同的缀-符串String。

如果有，那么这个缀-符串(String)就变成前缀(Prefix)，继续输入新的字符，否则就把这个缀-符串(String)写到词典中生成一个新的前缀(Prefix)，并给一个代码。

lzw编码原理
LZW（Lempel-Ziv-Welch）编码是一种无损数据压缩算法，它基于字典的概念来实现压缩。

LZW编码算法的原理如下：
1. 初始化字典：首先，创建一个初始字典，其中包含所有可能的单个输入符号（例如，字母、数字和符号）。

2. 获取输入符号：从输入数据中读取第一个输入符号作为当前字串。

3. 处理输入符号：检查当前字串是否存在于字典中：
- 如果存在，将下一个输入符号添加到当前字串末尾，以获得一个更长的字串。

然后返回到第3步，继续处理新的当前字串。

- 如果不存在，将当前字串的编码（即其在字典中的索引）输出，并将当前字串及其下一个输入符号添加到字典中。

然后返回到第2步，从下一个输入符号开始处理。

4. 重复步骤2和3，直到所有输入符号都被处理完。

5. 输出编码：输出所有处理过的编码，即压缩后的数据。

LZW编码算法的关键是利用字典来存储已经出现过的字串及其对应的编码。

通过在压缩过程中动态更新字典，LZW可以利用重复出现的字串来节约存储空间。

解压缩过程与压缩过程相反，通过对压缩后的编码逐个解码，然后动态构建字典来重构原始数据。

LZW编码的优势在于对于包含重复出现的字串的数据可以实现较高的压缩比率。

然而，它也可能由于字典的不断增长导致压缩后的数据比原始数据更大。

因此，在实际应用中，LZW
编码通常与其他压缩算法结合使用，例如在GIF图像压缩中的应用。

lzw和霍夫曼编码LZW（Lempel-Ziv-Welch）编码和Huffman编码是常见的无损数据压缩算法。

它们可以将数据以更高效的方式表示，并减少数据所占用的存储空间。

虽然两种编码算法有一些相似之处，但它们的工作原理和实施方法略有不同。

1.LZW编码：LZW编码是一种基于字典的压缩算法，广泛应用于文本和图像等数据的压缩。

它的工作原理是根据已有的字典和输入数据，将连续出现的字符序列转换为对应的索引，从而减少数据的存储空间。

LZW编码的过程如下：•初始化字典，将所有可能的字符作为初始词条。

•从输入数据中读取字符序列，并检查字典中是否已有当前序列。

•如果字典中存在当前序列，则继续读取下一个字符，将该序列与下一个字符连接成一个长序列。

•如果字典中不存在当前序列，则将当前序列添加到字典中，并输出该序列在字典中的索引。

•重复以上步骤，直到输入数据全部编码完成。

LZW编码的优点是可以根据实际数据动态更新字典，适用于压缩包含重复模式的数据。

2.霍夫曼编码：霍夫曼编码是一种基于频率的前缀编码方法。

它根据字符出现的频率构建一个最优二叉树（霍夫曼树），将出现频率较高的字符用较短的二进制码表示，出现频率较低的字符用较长的二进制码表示。

霍夫曼编码的过程如下：•统计输入数据中各个字符的频率。

•使用字符频率构建霍夫曼树，频率较高的字符在树的较低层，频率较低的字符在树的较高层。

•根据霍夫曼树，为每个字符分配唯一的二进制码，保持没有一个字符的编码是另一个字符编码的前缀。

•将输入数据中的每个字符替换为相应的霍夫曼编码。

•输出霍夫曼编码后的数据。

霍夫曼编码的优点是可以根据字符频率进行编码，使高频字符的编码更短，适用于压缩频率差异较大的数据。

总的来说，LZW编码和霍夫曼编码都是常见的无损数据压缩算法，用于减少数据的存储空间。

它们的选择取决于具体的场景、数据特点和应用需求。

多媒体技术LZW编码实验报告班级姓名学号实验名称：LZW算法的编程实现实验内容：用C++语言编写程序来实现LZW算法一、LZW定义：LZW就是通过建立一个字符串表,用较短的代码来表示较长的字符串来实现压缩. 字符串和编码的对应关系是在压缩过程中动态生成的,并且隐含在压缩数据中,解压的时候根据表来进行恢复,算是一种无损压缩.在本次实验中我们就进行了LZW编码以及译码简单算法的编写。

LZW编码又称字串表编码，是无损压缩技术改进后的压缩方法。

它采用了一种先进的串表压缩，将每个第一次出现的串放在一个串表当中，用一个数字来表示串，压缩文件只进行数字的存贮，则不存贮串，从而使图像文件的压缩效率得到了较大的提高。

LZW编码算法的原理是首先建立一个词典，即跟缀表。

对于字符串流，我们要进行分析，从词典中寻找最长匹配串，即字符串P在词典中，而字符串P+后一个字符C不在词典中。

此时，输出P对应的码字，将P+C放入词典中。

经过老师的举例，我初步知道了对于一个字符串进行编码的过程。

二、编码的部分算法与分析如下：首先根据需要得建立一个初始化词典。

这里字根分别为 A B C。

具体的初始化算法如下：void init()//词典初始化{dic[0]="A";dic[1]="B";dic[2]="C";//字根为A,B,Cfor(int i=3;i<30;i++)//其余为空{dic[i]="";}}对于编码算法的建立，则需先建立一个查找函数，用于查找返回序号：int find(string s){int temp=-1;for(int i=0;i<30;i++){if(dic[i]==s) temp=i+1;}return temp;}接下来就可以编写编码算法了。

void code(string str){init();//初始化char temp[2];temp[0]=str[0];//取第一个字符temp[1]='\0';string w=temp;int i=1;int j=3;//目前字典存储的最后一个位置cout<<"\n 编码为：";for(;;){char t[2];t[0]=str[i];//取下一字符t[1]='\0';string k=t;if(k=="") //为空，字符串结束{cout<<" "<<find(w);break;//退出for循环,编码结束}if(find(w+k)>-1){w=w+k;i++;}else{cout<<" "<<find(w);string wk=w+k;dic[j++]=wk;w=k;i++;}}cout<<endl;for(i=0;i<j;i++){cout<<setw(45)<<i+1<<setw(12)<<dic[i]<<endl;}cout<<endl;}三、译码是编码的逆过程：在译码中根缀表仍为A,B,C。

中文文本压缩的lzw算法
LZW算法（Lempel-Ziv-Welch 算法）是一种用于文本压缩的技术，它可以将文本文件中出现的重复字符串转换成唯一编码，从而有效地
实现文本文件的压缩。

LZW算法的运行过程分为两个步骤：初始字典的
构建和字符串的编码过程。

初始字典的构建：首先，创建一种字典，用于将原文件中的字符
串编码。

该字典以一系列整数作为键，以出现的字符串作为值，每当
遇到一个新的字符串时，就添加一个新的整数，作为它的编码。

字符串的编码过程：接下来，开始按照以下步骤对原文件中出现
的字符串进行编码：
1、从文件开头开始，读取一个字符，看看其是否已经在字典中；
2、如果已经存在，则查找下一个字符，将两个字符组成一个字符串，
继续查找；
3、如果不存在，则将该字符串加入字典，并且为之分配一个新的编码；
4、将其编码输出，然后继续查找下一个字符；
5、重复2-4直至文件末尾，从而完成文件的编码。

总之，LZW算法是一种有效的文本压缩技术，它可以很好地将文本
文件中出现的重复字符串进行压缩，从而有效地节约存储空间，并大
大提高文件传输的速度。

LZW编码算法详解LZW是一种字典压缩算法，用于无损数据压缩。

它是由Terry Welch在1977年提出的，主要用于无损压缩图像和文本数据。

LZW算法的特点是算法实现简单，压缩率高效。

LZW算法的基本原理是利用字典来存储已出现的文本片段，并使用字典中的索引来替代重复出现的片段。

初始时，字典中包含所有的单个字符。

算法从输入数据的第一个字符开始，不断扩充字典，直到处理完完整的数据流。

具体来说，LZW算法的编码流程如下：1.创建一个空字典，初始化字典中包含所有的单个字符。

2.读取输入数据流的第一个字符，将其作为当前字符。

3.从输入数据流中读取下一个字符，将其与当前字符进行拼接，得到当前字符串。

4.检查当前字符串是否在字典中，如果在字典中，则将当前字符串作为新的当前字符串，并继续读取下一个字符。

5.如果当前字符串不在字典中，将当前字符串的索引输出，并将当前字符串添加到字典中作为新的条目。

6.重复步骤3-5，直到处理完整的输入数据流。

LZW算法的解码流程与编码流程相似，但需要注意解码时字典的初始化方式。

解码时，初始字典只包含单个字符，不包含任何字符串。

解码算法的具体流程如下：1.创建一个空字典，初始化字典中包含所有的单个字符。

2.从输入编码流中读取第一个索引值，并将其作为上一个索引值。

3.在字典中找到当前索引值所对应的字符串，并输出。

4.如果已经读取完整个编码流，则解码结束。

5.否则，从输入编码流中读取下一个索引值，并将其作为当前索引值。

6.检查当前索引值是否在字典中，如果在字典中，则将上一个索引值和当前索引值对应的字符串进行拼接，得到新的解码字符串，并将其输出。

7.如果当前索引值不在字典中，将上一个索引值对应的字符串和上一个索引值拼接，得到新的解码字符串，并将其输出。

然后将新解码字符串添加到字典中作为新的条目。

8.将当前索引值作为上一个索引值，并继续重复步骤4-7，直到解码完成。

LZW算法的优点是能够在保持数据完整性的同时，显著减小数据的大小。

LZW编码的C/C++编码实现实验报告LZW就是通过建立一个字符串表,用较短的代码来表示较长的字符串来实现压缩. 字符串和编码的对应关系是在压缩过程中动态生成的,并且隐含在压缩数据中,解压的时候根据表来进行恢复,算是一种无损压缩.在本次实验中我们就进行了LZW编码以及译码简单算法的编写。

LZW编码又称字串表编码，是无损压缩技术改进后的压缩方法。

它采用了一种先进的串表压缩，将每个第一次出现的串放在一个串表当中，用一个数字来表示串，压缩文件只进行数字的存贮，则不存贮串，从而使图像文件的压缩效率得到了较大的提高。

LZW编码算法的原理是首先建立一个词典，即跟缀表。

对于字符串流，我们要进行分析，从词典中寻找最长匹配串，即字符串P在词典中，而字符串P+后一个字符C不在词典中。

此时，输出P对应的码字，将P+C放入词典中。

经过老师的举例，我初步知道了对于一个字符串进行编码的过程。

编码的部分算法如下：首先根据需要得建立一个初始化词典。

这里字根分别为 A B C。

具体的初始化算法如下：void init()//词典初始化{dic[0]="A";dic[1]="B";dic[2]="C";//字根为A,B,Cfor(int i=3;i<30;i++)//其余为空{dic[i]="";}}对于编码算法的建立，则需先建立一个查找函数，用于查找返回序号：int find(string s){int temp=-1;for(int i=0;i<30;i++){if(dic[i]==s) temp=i+1;}return temp;}接下来就可以编写编码算法了。

void code(string str){init();//初始化char temp[2];temp[0]=str[0];//取第一个字符temp[1]='\0';string w=temp;int i=1;int j=3;//目前字典存储的最后一个位置cout<<"\n 编码为：";for(;;){char t[2];t[0]=str[i];//取下一字符t[1]='\0';string k=t;if(k=="") //为空，字符串结束{cout<<" "<<find(w);break;//退出for循环,编码结束}if(find(w+k)>-1){w=w+k;i++;}else{cout<<" "<<find(w);string wk=w+k;dic[j++]=wk;w=k;i++;}}cout<<endl;for(i=0;i<j;i++){cout<<setw(45)<<i+1<<setw(12)<<dic[i]<<endl;}cout<<endl;}译码是编码的逆过程。

LZW 编码分析导航L ZW 编码分析 (1)缘起： (1)名词规范： (1)本文完成的主要工作 (1)L ZW编码原理 (2)L ZW解码原理 (3)问题及改进： (4)算法实现及分析 (6)关于作业以外的延拓： (10)参考文献： (11)缘起：LZW 是一种无损数据压缩算法，是对1978 年发表的LZ78 的改进。

LZW应用于Unix 系统的标准工具、GIF图片格式以及TIFF格式等。

同时LZW压缩算法对于较大规模的英文文本的压缩具有良好的效果，一般可以压缩到原来大小的一半。

然而LZW的专利曾一度限制了其使用范围，不过，LZW专利于2003年过期。

对事物的好奇心驱使我深入学习LZW 压缩和解压缩算法。

本文绝大部分的陈述来自于Dobb博士的论文以及技术博客、论坛以及维基百科。

名词规范：码书编解码时供查询、插入的字符串和整数索引的集合{(STRING,INDEX)}文本需要进行编码的数据结构编码序列编码后的整数序列码字表示字符串及其索引值的一种数据结构(STRING,INDEX)本文完成的主要工作当码书很大时，查询和编码的效率将有所下降。

查询的效率可以很直观的理解，编码效率的下降是指编码的结果是整数序列，其中将会出现较大的整数，如果不进行后续处理，需要较多的比特才能对其进行编码。

本文将结合TIF格式中的压缩原理，对Dobb博士所提及的LZW算法进行适当的改进，即，当码书容量达到一个容限值时，比如4096 = 210(13bit)，清空码书，并在编码序列中插入清除标志CLEAR，为原始数据字长(255 = 28)加1，并插入结束标志END，其大小为清除标志CLEAR加1，然后重新构造码书。

LZW编码原理LZW压缩编码如下所示1.STRING = get input character2.WHILE there are still input characters DO3. CHARACTER = get input character4. IF STRING+CHARACTER is in the string table then5. STRING = STRING+character6. ELSE7. output the code for STRING8. add STRING+CHARACTER to the string table9.IF table size reaches up to the predetermined MAX_SIZE10. renew table and append CLEAN and END label to the output11.END of IF12. STRING = CHARACTER13. END of IF14.END of WHILE15.output the code for STRING其中9~11行根据TIF格式压缩原理而添加的步骤，图1是其编码示例，由于输入文本很短，不会导致码书容量达到上限值，因而不会运行9~11行所示代码。

班级 __ __ 学号__姓名 __ ___评分__________1．实验名称LZW编码与解码算法2．实验目的2.1通过实验进一步掌握LZW编码的原理；2.2 用C/C++等高级程序设计语言实现LZW编码。

3．实验内容步骤或记录（包括源程序或流程和说明等）3.1 实验原理（1）在压缩过程中动态形成一个字符列表（字典）。

（2）每当压缩扫描图像发现一个词典中没有的字符序列，就把该字符序列存到字典中，并用字典的地址（编码）作为这个字符序列的代码，替换原图像中的字符序列，下次再碰到相同的字符序列，就用字典的地址代替字符序列3.2实验步骤LZW编码算法的具体执行步骤如下：步骤1：开始时的词典包含所有可能的根(Root)，而当前前缀P是空的；步骤2：当前字符(C) ：=字符流中的下一个字符；步骤3：判断缀-符串P+C是否在词典中(1) 如果“是”：P ：= P+C // (用C扩展P) ；(2) 如果“否”①把代表当前前缀P的码字输出到码字流;②把缀-符串P+C添加到词典;③令P ：= C //(现在的P仅包含一个字符C);步骤4：判断码字流中是否还有码字要译(1) 如果“是”，就返回到步骤2；(2) 如果“否”①把代表当前前缀P的码字输出到码字流;②结束。

3.3 源程序#include<iostream>#include<string>using namespace std;const int N=200;class LZW{private: string Dic[200];//存放词典int code[N];//存放编码过的码字public: LZW(){//设置词典根Dic[0]='a';Dic[1]='b';Dic[2]='c';string *p=Dic;//定义指针指向词典中的字符} void Bianma(string cs[N]);//进行编码int IsDic(string e);//判断是否在词典中int codeDic(string f);void display(int g);//显示结果};void LZW::Bianma(string cs[N]){string P,C,K;P=cs[0];int l=0;for(int i=1;i<N;i++){C=cs[i];//当前字符(C) ：=字符流中的下一个字符 K=P+C;if(IsDic(K)) P=K;//P+C在词典中，用C扩展P else{//P+C不在词典中code[l]=codeDic(P);Dic[3+l]=K;//将P+C加入词典P=C;l++;}if(N-1==i)//如果字符流中没有字符需要编码code[l]=codeDic(P);}display(l);}int LZW::IsDic(string e){//如果字符流中还有字符需要编码for(int b=0; b<200; b++){ if(e==Dic[b]) return 1; }return 0;}int LZW::codeDic(string f){int w=0;for(int y=0;y<200;y++)if(f==Dic[y]){w=y+1;break;}return w;}void LZW::display(int g){cout<<"经过LZW编码后的码字如下："<<endl;for(int i=0;i<=g;i++)cout<<code[i];cout<<endl;cout<<"经LZW编码后的词典如下："<<endl;for(int r=0;r<g+3;r++)cout<<r+1<<Dic[r]<<endl;}int main(){LZW t;string CSstream[N];// 存放要进行LZW编码的字符序列int length;// 要进行LZW编码的字符序列长度cout<<"请输入所求码子序列的长度：";cin>>length;while(length>=N){cout<<"该长度太长，请重新输入：";cin>>length;}cout<<"请输入要进行LZW编码的字符序列："<<endl; for(int a=0;a<length;a++)cin>>CSstream[a];t.Bianma(CSstream);return 0;}4．实验环境（包括软、硬件平台）硬件：装有32M以上内存MPC；软件：Windows XP操作系统、Visual C++高级语言环境。