第三章高等数学基础知识-空间解析几何题库1-2-10

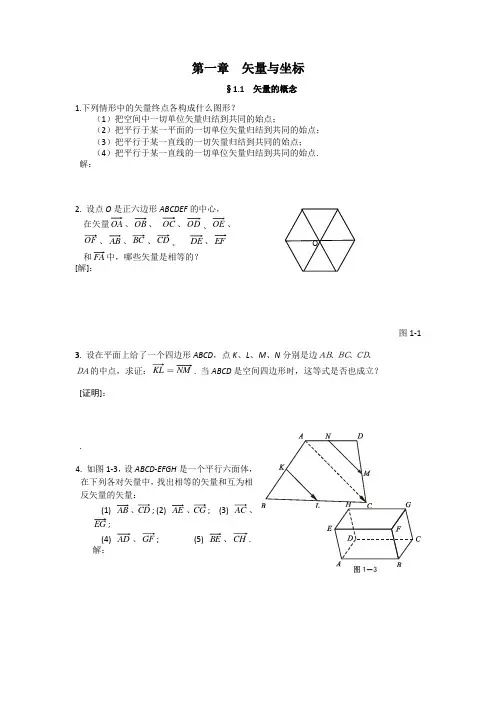
第一章矢量与坐标§1.1 矢量的概念1.下列情形中的矢量终点各构成什么图形？（1）把空间中一切单位矢量归结到共同的始点；（2）把平行于某一平面的一切单位矢量归结到共同的始点；（3）把平行于某一直线的一切矢量归结到共同的始点；（4）把平行于某一直线的一切单位矢量归结到共同的始点.解：2. 设点O是正六边形ABCDEF的中心，在矢量OA、OB、OC、OD、OE、OF、AB、BC、CD、DE、EF和FA中，哪些矢量是相等的？[解]：图1-13. 设在平面上给了一个四边形ABCD，点K、L、M、N分别是边ＡＢ、ＢＣ、ＣＤ、ＤＡ的中点，求证：KL＝NM. 当ABCD是空间四边形时，这等式是否也成立？[证明]：.4. 如图1-3，设ABCD-EFGH是一个平行六面体，在下列各对矢量中，找出相等的矢量和互为相反矢量的矢量：(1) AB、CD; (2) AE、CG; (3) AC、EG;(4) AD、GF; (5) BE、CH.解：§1.2 矢量的加法1.要使下列各式成立，矢量b a ,应满足什么条件？ （1=+ （2+=+ （3-=+ （4+=- （5= 解：§1.3 数量乘矢量1 试解下列各题．⑴ 化简)()()()(→→→→-⋅+--⋅-b a y x b a y x ．⑵ 已知→→→→-+=3212e e e a ，→→→→+-=321223e e e b ，求→→+b a ，→→-b a 和→→+b a 23．⑶ 从矢量方程组⎪⎩⎪⎨⎧=-=+→→→→→→by x ay x 3243，解出矢量→x ，→y ．解：2 已知四边形ABCD 中，→→→-=c a AB 2，→→→→-+=c b a CD 865，对角线→AC 、→BD 的中点分别为E 、F ，求→EF ． 解：3 设→→→+=b a AB 5，→→→+-=b a BC 82，)(3→→→-=b a CD ，证明：A 、B 、D 三点共线． 解：4 在四边形ABCD中，→→→+=baAB2，→→→--=baBC4，→→→--=baCD35，证明ABCD为梯形．解：6. 设L、M、N分别是ΔABC的三边BC、CA、AB的中点，证明：三中线矢量AL, BM, CN可以构成一个三角形.7. 设L、M、N是△ABC的三边的中点，O是任意一点，证明OBOA++OC=OL+OM+ON.解：8. 如图1-5，设M是平行四边形ABCD的中心，O是任意一点，证明OA+OB+OC+OD＝4OM.解：9在平行六面体ABCDEFGH（参看第一节第4题图）中，证明→→→→=++AGAHAFAC2．证明：．10.用矢量法证明梯形两腰中点连续平行于上、下两底边且等于它们长度和的一半．解11. 用矢量法证明，平行四边行的对角线互相平分.解12. 设点O 是平面上正多边形A 1A 2…A n 的中心，证明: 1OA +2OA +…+n OA ＝0.解,13．在12题的条件下，设P 是任意点，证明 证明：§1.4 矢量的线性关系与矢量的分解1．在平行四边形ABCD 中，（1）设对角线,,b BD a AZ ==求.,,,DA CD BC AB 解（2）设边BC 和CD 的中点M 和N ，且q AN P AM ==,求CD BC ,。

最新文件---------------- 仅供参考--------------------已改成-----------word 文本 --------------------- 方便更改空间解析几何与矢量代数小练习一 填空题 5’x9=45分1、 平行于向量)6,7,6(-=a 的单位向量为______________.2、 设已知两点)2,0,3()1,2,4(21M M 和，计算向量21M M 的模_________________， 方向余弦_________________和方向角_________________3、以点(1,3,-2)为球心，且通过坐标原点的球面方程为__________________.4、方程0242222=++-++z y x z y x 表示______________曲面.5、方程22x y z +=表示______________曲面.6、222x y z +=表示______________曲面.7、 在空间解析几何中2x y =表示______________图形.二 计算题 11’x5=55分1、求过点(3,0,-1)且与平面3x-7y+5z-12=0平行的平面方程.2、求平行于x 轴且过两点(4,0,-2)和(5,1,7)的平面方程.3、求过点(1,2,3)且平行于直线51132-=-=z y x 的直线方程.4、求过点(2,0,-3)且与直线⎩⎨⎧=+-+=-+-012530742z y x z y x 垂直的平面方5、已知：k i OA 3+=，k j OB 3+=，求OAB ∆的面积。

参考答案一 填空题1、⎩⎨⎧⎭⎬⎫-±116,117,1162、21M M =2,21cos ,22cos ,21cos ==-=γβα,3,43,32πγπβπα=== 3、14)2()3()1(222=++-+-z y x4、以(1,-2,-1)为球心,半径为6的球面5、旋转抛物面6、 圆锥面7、 抛物柱面二 计算题1、04573=-+-z y x2、029=--z y3、531221-=-=-z y x 4、065111416=---z y x5 219==∆S最新文件---------------- 仅供参考--------------------已改成-----------word 文本 --------------------- 方便更改赠人玫瑰，手留余香。

高等数学（ B ）—向量代数与空间解析几何练习题及解答1、 已知 M 11,2,3 ， M 2 0,1, 2 ，M 1M 2 的坐标式？ M 1M 2 ？与 M 1M 2 平行的单位向量？方向余弦？[解]：1） M 1M 20 1,1 2, 2 31,1,5M 1M 2 21 222)1 5 273） cosx 2 x 1 1,cosy 2 y 1 1,cosz 2 z 1 5M 1M 227 M 1M 227M 1M 2274）与 M 1M 2 平行的单位向量为：cos ,cos ,cos1 , 1 , 5 。

272727x 1y z 1 x y 1z 2 2、 设直线n4与直线1平行，求 n,m 。

2m3[解 ] ： s 12,n,4 , s 2 m,1,3 ，因为两直线平行，r m 1 n 1 p 1 2 n 4 4 3 所以 l 1 / /l 2s 1 / / s 2s 1s 2。

m 2n 2 p 2n, m2m 1 333Ax y 2z 1 与平面： 3x y z3垂直，求 A 。

、 已知平面：[解 ] ： n 1A,1, 2 , n 2 3, 1,1 ，因为两平面垂直，所以12n 1 n 2 n 1 n 2 0 A 1 A 2 B 1B 2 C 1C 2 0 A 3 1 1 210 A14、 已知平面x 1 y z 1 : x By 3z 1 0 与直线4垂直，求 B ， m 。

m6[ 解 ]： n 1,B, 3 , s m,4,6 ，因为垂直，所以有n/ / s n s 0m4 6 。

1BB2, m 235、 求由 a 1,2,3 , b 1,2,4 为邻边组成的平行四边形的面积。

[ 解] ：由两向量叉积的几何意义知：以a ，b 为邻边组成的平行四边行的面积S a bi j k86, 43,222,7,4a b 123，因为124故 S a b22269 。

7426、求以A x1, y1, z1, B x2, y2, z2, C x3 , y3, z3为顶点的三角形面积。

第三章 常见曲面习题3.11.证明：如果2220a b c d ++->，那么由方程2222220x y z ax by cz d ++++++=给出的曲面是一球面，求出它的球心坐标和半径。

证明：将方程配方得222222()()()x a y b z c a b c d +++++=++-，由2220a b c d ++->，得到方程表示球心是(,,)a b c ---2.求过三点(3,0,0),(0,2,0),(0,0,1)的圆的方程。

解：空间中的圆可由过三点(3,0,0),(0,2,0),(0,0,1)的一个球面和一个平面的交线表示，设过该三点的球面方程为2220x y z ax by cz d ++++++=，得到930,420,10a d b d c d ++=⎧⎪++=⎨⎪++=⎩球面方程为22294(1)032d dx y z x y d z d ++++---++=，其中d 任意。

过该三点的平面方程是132x yz ++=，所以所求圆的方程可以为 2226()2(9)3(4)6(1)60,23660x y z d x d y d z d x y z ⎧++-+-+-++=⎨++-=⎩ 其中d 任意。

3.证明曲线24224324,1,(,)1,1t x t t t y t t t t z t t ⎧=⎪++⎪⎪=∈-∞+∞⎨++⎪⎪=⎪++⎩在一球面上，并此球面方程。

证明：因为曲线满足2322222224242422242424()()()111()(1)11tt t x y z t t t t t t t t t t y t t t t++=++++++++=++==++++即22211()24x y z +-+=，所以曲线在一个球面上。

4.适当选取坐标系，求下列轨迹的方程（1）到两定点距离之比等于常数的点的轨迹； （2）到两定点距离之和等于常数的点的轨迹； （3）到定平面和定点等距离的点的轨迹。

空间解析几何和多元微分学练习题参考答案1．若®®®®++=k j i a 863，2=®b ，则与®a ，x 轴均垂直的向量=®b þýüîíì-±56,58,0。

2．以点A )0,0,2(，B )0,3,0(，C )6,0,0(，D )8,3,2(为顶点的四面体的体积V=14。

3．曲线ïîïíì=+-=-+4)2(4)2(2222y x z x 在yoz 面上的投影曲线方程为：ïîïíì=+-±=+±044422x y z ，投影柱面方程为：44422+-±=+±y z 。

4．xoz 面上的曲线19422=-z x 分别绕x 轴和z 轴旋转所成旋转曲面方程为：1994222=--z y x ，1944222=-+z y x 。

5．求两平面0622:1=+-+z y x p ，884:2=-+-z y x p 所成二面角的角平分面方程。

解：法一，设),,(z y x P 为所求平面上任意一点，则由题意有：2222228)1(4884)2(21622+-+-+-=-+++-+z y x z y x消去绝对值得 )884()6222(3-+-±=+-+z y x z y 即026147010257=-+-=+++z y x z y x 和法二，所求平面过两平面1p 与2p 的交线，故可设其方程为：0)622(884=+-++-+-z y x z y x l在该平面上任取一点， 如令4430--===l lz y x 可得，然后由点)443,0,0(--l l 到两平面的距离相等可解得3±=l ，从而得到所求平面方程。

第一章 函数、极限与连续一、 判断题:1．极限)(lim 0x f x x →存在的充要条件是)0(0-x f 与)0(0+x f 都存在。

（ ）2．如果)0(0-x f 与)0(0+x f 都存在且相等，则)(lim 0x f x x →存在。

（ ）3．如果函数)(x f 在0x 处既左连续且右连续，则)(x f 在0x 连续。

（ ） 4．如果)(lim 0x f x x →存在，则)(x f 在0x 连续。

（ ）5．如果函数)(x f 在0x 连续，则)(lim 0x f x x →存在。

（ ）6．极限 2200limy x xyy x +→→存在 。

（ ）7．如果)(x f 在()b a ,内连续，则)(x f 在()b a ,内必有最大值和最小值。

（ ） 8．如果)(x f 在[]b a ,内连续，则)(x f 在[]b a ,内必有最大值和最小值。

（ ） 9．极限 ()e x xx -=-→1lim 0。

（ ）10．极限21946853lim 2323=-++-∞→x x x x x 。

（ ） 二、 填空题:1．函数1)3ln(2222-++--=y x y x y 的定义域是 。

2. 函数4192222-++--=y x y x y 的定义域是 。

3.若⎪⎩⎪⎨⎧<=>+=0,00,,1)(x x x x x f π，则=-)]}1([{f f f 。

4. 函数 x y 2sin ln =的复合过程是 。

5. 一切初等函数在其 内都是连续的。

6. 设arctgx x y 2-=，则)(lim x y x --∞→= 。

7. 如果322sin 3lim0=→x mx x ，则m = 。

8. 设⎪⎩⎪⎨⎧≥-<<≤-+=2,2221,1,32)(2x x x x x x x x f ，则)(lim 1x f x →= 。

9. 函数11)(2+-=x x x f 的间断点是 。

向量代数与空间解析几何第一部分 向量代数___线性运算[内容要点]:1. 向量的概念.2. 向量的线性运算.3. 向量的坐标，利用坐标作向量的线性运算.[本部分习题]1. 指出下列各点所在的坐标轴、坐标面或哪个卦限.2. 求点(1,3,2)--关于点(1,2,1)-的对称点坐标.3. 求点(4,3,5)M --到各坐标轴的距离.4. 一向量的起点为(1,4,2)A -,终点为(1,5,0)B -,求AB →在x 轴、y 轴、z 轴上的投影,并求||AB →。

5. 已知两点1M 和2(3,0,2)M ,计算向量12M M −−→的模、方向余弦和方向角.6． 已知{3,5,4},{6,1,2},{0,3,4},a b c →→→==-=--求234a b c →→→-+及其单位向量.7．设358,247,54,a i j k b i j k c i j k →→→→→→→→→→→→=++=--=--求向量43l a b c →→→→=+-在x 轴上的投影以及在y 轴上的分向量. 第二部分 向量代数___向量的“积”[内容要点]:1.向量的数量积、向量积的概念、坐标表示式及其运算规律。

2.向量的混合积的概念、坐标表示式及其几何意义。

3.向量垂直、平行、共面的条件.[本部分习题]1． 设{3,1,2},{1,2,1},a b →→=--=-求：（1）;(2);(3)cos(,);(4)Pr ;(5)Pr .a b a b a b a b j b j a →→→→→→→→⋅⨯2． 设{2,3,1},{1,1,3},{1,2,0},a b c →→→=-=-=-求：3． 112233a b a b a b ≥++ 其中,(1,2,3)i i a b i =均为实数，并指出等号成立的条件.4．设{3,5,2},{2,1,9},a b →→=-=试求λ的值,使得:（1）a b λ→→+与z 轴垂直；（2）a b λ→→+与a →垂直，并证明此时||a b λ→→+取最大值。

第三章高等数学基础知识-空间解析几何题
库1-1-8
问题：
[单选]方程表示（）。

A.锥面
B.单叶双曲面
C.双叶双曲面
D.椭圆抛物线
问题：
[单选]曲面x2-y2=z在xOz平面上的截痕是（）。

A.A
B.B
C.C
D.D
xOz平面y=0。

问题：
[单选]方程表示（）。

A.椭球面
B.平面上椭圆
C.椭圆柱面
D.椭圆柱面在平面上的投影曲线
题干中的方程表示平面y=1上的椭圆. (安徽11选5 https://)
问题：
[单选]设空间直线的对称式方程为，则该直线必（）。

A.过原点且垂直于x轴
B.过原点且垂直于y轴
C.过原点且垂直于z轴
D.过原点且平行于x轴
问题：
[单选]在空间直角坐标系中表示（）。

A.一个点
B.两条直线
C.两个平面的交线，即直线
D.两个点
问题：
[问答题]设，且a≠b，记｜a-b｜=m，求a-b与x轴正方向的夹角的余弦值。

问题：
[问答题]已知空间三点A（0，2，3），B（-2，1，6），C（1，-1，5）。

（1）求以向量为一组邻边的平行四边形的面积S；
（2）若向量a分别与向量垂直，且，求向量a的坐标。

常考题型及解法与技巧题型一 向量的运算1 [2012大纲]（1）设 22,5,(,)3a b a b π=== ，则λ= 时，向量17m a b λ=+ 与3n a b =- 相互垂直；（2）设23m a b =+ ，3n a b =- ， 12,1,(,)3a b a b π=== ，则m n ⨯= ； （3）设()2a b c ⨯⋅= ，则[()()]()a b b c c a +⨯+⋅+=2 [2012常考题型]设32,1,2,3A a b c a b c =+-=== ，a 与b 的夹角为3π，b 与c 的夹角为3π，c 与a 的夹角为2π，则A = 题型二 求平面、直线的方程（一）平面方程１、[2012大纲Ｐ96] 求过点(1,2,1)且与直线1210:10x y z L x y z +-+=⎧⎨-+-=⎩和220:0x y z L x y z -+=⎧⎨-+=⎩平行的平面方程．2、[2012大纲Ｐ96] 一个平面过两个平面1:50x y z ∏++=和2:40x z ∏-+=的交线，且与平面3:48120x y z ∏--+=成45 角，求此平面方程．3、[2012精解Ｐ58] 设平面∏过原点和点(6,3,2)M -，且与平面1:428x y z ∏-+=垂直，求此平面方程．4、［北航Ｐ357] 求以下平面方程．(1)过点(1,2,3)且与直线112211x y z +-+==-垂直的平面方程． (2)过点(2,5,1)-且平行于直线1123:1031x y z L ---==和2132:245x y z L ++-==的平面方程． (3)过平面1:2310x y z ∏--+=与平面2:0x y z ∏++=的交线且与平面2∏垂直的平面方程．5、[北航Ｐ357] 求椭球面2222321x y z ++=上点0000(,,)P x y z 处的切平面∏的方程，使平面过已知直线6321:212x y z L ---==-． 6、[2010Ｐ117] 求过点(1,2,1)M -且与直线2,34,1x t y t z t =-+=-=-垂直的平面方程7、[第四届（2013）全国预赛] 求通过直线2320:55430x y z L x y z +-+=⎧⎨+-+=⎩的两两相互垂直的平面1∏和2∏，使其中一个平面过点(4,3,1)-．（二）直线方程１、[2012大纲Ｐ96] 设直线l 过点(1,2,1)A 且与直线111:321x y z l -+==垂直，与直线2:2x l y z ==相交，求直线l 的方程．２、[北航Ｐ355] 求过点(1,2,3)A --且平行于平面:62310x y z ∏--+=又与直线113:325x y z L -+-==-相交的直线方程． ３、[2012精解Ｐ59] 求过点(1,2,3M -，垂直于直线:456x y z l ==且平行于平面:789100x y z ∏+++=的直线方程．练习：[北航Ｐ354] 求过点(1,0,2)P -且与平面:3460x y z ∏+-+=平行，又同直线32:141x y z L -+==垂直的直线方程． ４、[2012精解Ｐ59] 求经过点(2,3,1)P -且与直线12:345x y z L -+==垂直相交的直线方程． 练习：[北航Ｐ354] 求过点(2,1,3)P 且与直线11:321x y z L +-==-垂直相交的直线方程． 5、[北航Ｐ356] 在平面:10x y z ∏+++=内求垂直于直线10:20y z L x z -+=⎧⎨+=⎩的直线方程． 题型三 点、线、面的关系１ [2012大纲Ｐ97] （１）已知平面29x ky z +-=与平面230x y z -+=的夹角为4π，求k ． （２）求点(1,2,3)P 到平面:23410x y z ∏-+-=的距离． （３）求直线3230:3230x y L y z --=⎧⎨-+=⎩与平面:1021130x y z ∏+--=的夹角．（4）求点(1,0,1)P -到直线3:3270x y L x y z -=⎧⎨+++=⎩的垂直距离． 练习：［ＢＨＰ358］求点(1,1,0)P -到直线2330:0y z L x y --=⎧⎨-=⎩的距离． 2、[2012大纲Ｐ98] (1)直线13:234x y z l +==与直线2122:112x y z l -+-==的关系是（ ） Ａ．相互垂直 Ｂ．斜交 Ｃ．互相平行 Ｄ．异面直线（2）设直线3210:21030x y z L x y z +++=⎧⎨--+=⎩，平面:4220x y z ∏-+-=，则Ａ．L 平行于∏ Ｂ．L 在∏上 Ｃ．L 垂直于∏ Ｄ．L 与∏斜交3、[北航Ｐ358]求直线11:011 x y zL -==与22:210x y zL+==-之间的距离．练习：（１）[2010Ｐ119]求异面直线131 :210 x y zL --==与212:101x y zL+-==之间的最短距离．（2）[第二届全国数学竞赛（2010）预赛]求直线10 :x yLz -=⎧⎨=⎩与直线2213:421x y zL---==--的距离．题型四求曲面的方程１、[2012大纲Ｐ98]求直线2:203x y zL-==绕z轴旋转一周所得旋转曲面的方程．2、[2012大纲Ｐ99]求以曲线2224:1x y zx y z⎧++=Γ⎨++=⎩为准线，母线平行于z轴的柱面方程．３、[北航Ｐ359]求准线是2225:x yz⎧+=Γ⎨=⎩，母线平行于向量(5,3,2)l=的柱面方程．４、[北航Ｐ359]设柱面的准线方程为2222221:222x y zx y z⎧++=⎪Γ⎨++=⎪⎩，而母线的方向矢量为{}0,0,1，求此柱面方程．５、[北航Ｐ359]设曲线222:x yz⎧-=Γ⎨=⎩，（１）求绕x轴旋所形成的旋转面方程；（２）求绕y轴旋转所形成的旋转面方程．题型五投影曲线1、[2012大纲Ｐ99]设曲线2222244:8312x y z zx y z z⎧++=⎪Γ⎨-+=⎪⎩，求它在xoy坐标面上的投影方程．2、[ＢＨＰ359]求22:20y z xx y z⎧+=Γ⎨+-=⎩在三个坐标面上的投影方程．3、[2012精解Ｐ60]求直线11:111x y zL--==-在平面:210x y z∏-+-=上的投影直线l的方程，并求l绕y轴旋转一周所成曲面的方程．４、[2012大纲Ｐ97]求直线10:10x y zLx y z+--=⎧⎨-++=⎩在平面:0x y z∏++=上的投影直线的方程．。

1. 过点M o （1，1-，1）且垂直于平面01201=+++=+--z y x z y x 及的平面方程．39．02=+-z y3． 在平面02=--z y x 上找一点p ，使它与点),5,1,2()1,3,4(-)3,1,2(--及之间的距离相等．7．)51,1,57(．5．已知：→→-AB prj D C B A CD，则)2,3,3(),1,1,1(),7,1,5(),3,2,1(= （ ）A ．4B ．1C ．21D ．2 7．设平面方程为0=-y x ，则其位置（ ）A ．平行于x 轴B ．平行于y 轴C ．平行于z 轴D ．过z 轴． 8．平面0372=++-z y x 与平面0153=-++z y x 的位置关系（ ） A ．平行 B ．垂直 C ．相交 D ．重合 9．直线37423zy x =-+=-+与平面03224=---z y x 的位置关系（ ） A ．平行 B ．垂直 C ．斜交 D ．直线在平面内 10．设点)0,1,0(-A 到直线⎩⎨⎧=-+=+-07201z x y 的距离为（ ）A ．5B ．61 C ．51 D ．81 5．D 7．D 8．B 9．A 10．A ．3．当m=_____________时，532+-与m 23-+互相垂直．4．设++=2，22+-=，243+-=，则)(b a p r j c += ．4． 过点），，（382-且垂直平面0232=--+z y x 直线方程为______________． 10．曲面方程为：44222=++z y x ，它是由曲线________绕_____________旋转而成的．3．34-=m ； 4．2919 9．332212--=+=-x y x ； 10．曲线1422=+z y 绕z 轴旋转而成．1．设{}{}{}0,2,1,3,1,1,1,3,2-=-=-=，则=⨯⨯)(（ ） A ．8 B ．10 C ．{}1,1,0-- D ．{}21,1,23．若==-+=，则14//236（ ） A ．)4612(-+± B ．)612(+± C ．)412(-± D ．)46(-± 4．若ϕ与，则3121321)2,1,2(),1,2,2(),1,1,1(M M M M M M M （ ） A ．6π B ．2π C ．3π D ．4π6．求平面062=-+-z y x 与平面052=-++z y x 的夹角（ ） A ．2π B ．6π C ．3π D ．4π 8．设点⎩⎨⎧=-+-=+-+-04201)2,1,3(z y x z y x l M o ，直线，则M O 到l 的距离为（ ）A ．223 B ．553 C ．453 D ．229．直线夹角为与平面62241312=++-=-=-z y x z y x （ ） A ．30o B ．60o C ．90oD ．65arcsin1．D 3．A 4．C 6．C 8．A 9．D7．求与平面4362=+-z y x 平行平面，使点)8,2,3(为这两个平面公垂线中点． 3．确定k 值，使三个平面：328,1423,23=--=++=+-z y x z y x z y kx 通过同一条直线．5．求以向量i k k j j i +++,,为棱的平行六面体的体积．7．与平面0522=+++z y x ，且与三个坐标面所构成的四面体体积为1的平面方程_____________________．8．动点到点（0,0,5）的距离等于它到x 轴的距离的曲面方程为________________． 9．曲面方程：259916222=--z y x 则曲面名称为________________．10．曲线⎪⎩⎪⎨⎧-+-=--=2222)1()1(2y x z yx z 在y z 面上的投影方程______________．1．设32+-=，+=2，++-=，则与+是否平行__________．1．不平行7．33222±=++z y x ； 8．25102-=-z x ；9．双叶双曲面； 10．⎩⎨⎧==+--++02342222x z y z yz y练习题选参考答案1．两非零向量→a 、→b 垂直，则有0=⋅→→b a 或0Pr =→→a j b；平行则有0=⨯→→b a 或→→=b a λ或两向量对应坐标成比例。