当前位置：文档之家 › 大学物理课件-固体中的电子

大学物理课件-固体中的电子

  • 格式：ppt
  • 大小：416.00 KB
  • 文档页数：29

下载文档原格式

  / 29

合集下载

大学物理：第13章-固体中的电子

大学物理：第13章-固体中的电子

真空能级
A
逸
EF
出
功
2
费米能级(能量)
EF
(3
)2 2/3
2m
n 2/3 s
取决于 ns 。
费米能量 EF ~ eV
在此狭小能量区间，密集排布着 (自由电子数 /2) 个能级，所以自 由电子的能量分布是准连续的。
费米速度 vF
EF
1 2
mvF2
,
vF
2EF ~ 106 m/s m
即使在绝对零度下，电子仍然剧烈地运动着。
二、固体导电性能的能带论解释：
由价电子填充的满带（或最低能带）称为价带。
有空量子态存在的能带（可以导电）叫导带。
能带之间没有量子态存在的区域叫禁带。
Na
3p
禁带
3s
价带 (导带)
金刚石 导带
禁带 价带
Si
导带 禁带 价带
导体有未填满的价带，当有外加电场时，价带电
子被加速，从电场中获得能量，可跃迁至价带中较高
的空能级，因而能够形成电流。
Na
3p
禁带
3s
价带 (导带)
金刚石 导带
禁带 价带
Si
导带 禁带 价带
绝缘体价带填满, 价带电子若想跃迁至高能级 (在 导带内)，必须越过很宽的禁带 Eg，一般电场不能提供 这么多能量，所以绝缘体不导电，但有击穿现象。
半导体虽然价带也填满，但禁带宽度 Eg 很小，价 带电子相对容易进入导带， 因此导电性能介于导体和 绝缘体之间。
二、自由电子气的费米能量：
周期性变条件，定态薛定谔方程
2 2m
2
x2
2
y2
2
z2
E

大学物理_4固体中电子

大学物理_4固体中电子

一个整数坐标点 对应一个状态
整数坐标点的个数 与体积数相当
状态空间内整数坐标点的个数对应其体积， 所以状态空间内体积就是状态数目。
考虑自旋以后，小于能量 E 的状态数目应为
N E21 84 3R 31 32m e3/2L 3E 2h 33 /2
所有自由电子按能量从低到高占据可能的状态， 最高能量达到 EF ---费米能量或能级
N1
3
2me
3/2
L3EF3/2
2h3
EF
(32)2/3
2 2me
n2/3
其中 n 金属内自由电子数密度
铜电子数密度 ~ 8.491028/m3
n
N L3
N V
EF ~7.05eV
• 能量区间 E~E+dE 电子数目百分比
N EdE N E N
dN E N
2E3F 3/2E1/2dE
EEF
三、 导体和绝缘体（ conductor& insulator)
导体 价带或导带
导带 绝缘体 ~ 5eV
价带
半导体
导带 0.2~3eV
价带
导带
导 体 存在不满带
在外电场的作用下, 大量共有化电子很易获得能量, 形成集体的定向流动(电流).
绝缘体 没有不满带
在外电场的作用下, 共有化电子很难接受外电场的 能量，形不成电流。
U (x) U (x)
布拉格衍射极大条件 2dsinn n 整数
e ikx
E p2 h2k2 2m 2m
反射极大 2an k n a来自n1,2,3,......
这种能量的电子不能自由传播
2 / a / a 禁带
E
E h2k 2 2m

《固体中的电子》PPT课件

《固体中的电子》PPT课件

B
在原子的 L 壳层中，电子可能具有的四个量子数
(n，l，ml，ms)是
(1) (2，0，1，1/2)。 (2) (2，1，0，-1/2)。 (3) (2，1，1，1/2)。 (4) (2，1，-1，-1/2)。
以上四种取值中，哪些是正确的？ (A) 只有 (1)、(2) 是正确的。 (B) 只有 (2)、(3) 是正确的。 (C) 只有 (2)、(3)、(4) 是正确的。 (D) 全部是正确的。
(B) n = 3，l = 1，ml = -1，ms = -1/2。
(C) n = 1，l = 2，ml = 1，ms = -1/2。
(D) n = 1，l = 0，ml = 1，ms = -1/2。
B
直接证实了电子自旋存在的最早的实验之一是 (A) 康普顿实验。 (B) 卢瑟福实验。 (C) 戴维逊 - 革末实验。 (D) 斯特恩 - 盖拉赫实验。
1s，2s，3s 电子轨道角动量为
l l 1 0 0 1 0
2p，3p 电子轨道角动量为
l l 1 1 1 1 2
在 z 方向的投影可以为
m l， 0 ，
第13章 固体中的电子 (Electrons in solid)
固体一般指晶体，是物质的一种凝聚态， 它的电性质、磁性质、甚至力性质都与其中的 电子有关。
可解释，电子先填入 4s，后填入 3d 的特例。
1s，2s，2p，3s，3p，4s，3d，4p，5s，4d，5p，6s， 4f，5d，6p，7s，6d，5f，7p，6f，7d
原子中电子排布实例表
原子 序数
元素
K s
L
s
p
M
s
p
1H 1
2 He 2

大学物理_4固体中的电子

大学物理_4固体中的电子

布拉格衍射极大条件 2dsinn n 整数
e ikx
E p2 2k2 2m 2m
反射极大 2an k n
a
n1,2,3,......
这种能量的电子不能自由传播
2 / a / a
禁带
E
2k 2 E
2m
/ a 2 / a k
2Ln
k n L
k La
E
禁带
能带
2 / a / a
Ea ~ 10-2 eV
在空穴型半导体中
空穴 . . . . . . 多数载流子 电子 . . . . . . 少数载流子
3. n型化合物半导体
例如, 化合物 GaAs中掺Te, 六价Te替代五价As可形成施主能级, 成为n型 GaAs杂质半导体.
4. p型化合物半导体
例如, 化合物 GaAs中掺Zn, 二价Zn替代三价Ga可形成受主能级, 成为p型 GaAs杂质半导体.
dNE V
g(E)dE 0
EEF EEF
小于费米能量，电子数=状态数 小于费米能量态，电子占据几率 1
大于费米能量态，电子占据几率 0
f(E) 1
T= 0
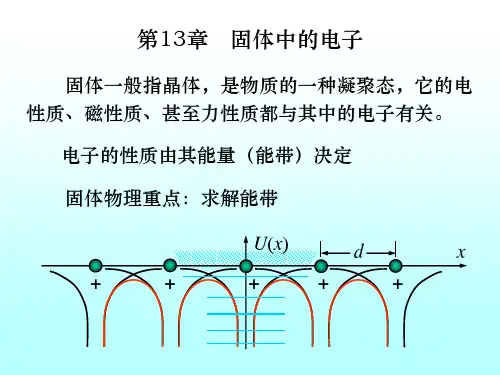
0 系统一、能带 (energy band) 自由电子近似过于简单 要考虑与晶格散射
U (x) U (x)
• (nx, ny, nz) 量子数 表示电子状态 • 相同的能量对应许多不同的状态 (简并态)
(2,1,1) (1, 2,1) (1,1, 2)
• 自由电子气体(量子气体), 按能量分布 ?
N个电子如何排布的问题 • 能量最低原则 • 泡利不相容原理
每个(nx, ny, nz),占据一个电子 (不考虑自旋)
三、 导体和绝缘体（ conductor& insulator)

《固体中的电子》课件

《固体中的电子》课件

《固体中的电子》PPT课件
固体中的电子PPT课件大纲： 1. 概述固态物理学 2. 电子在固体中的行为介绍 3. 固体的电子能带结构
电子能带结构
1
能带间隙
能带间隙决定了材料的导电性质，从绝
费米能级
2
缘体到导体的转变。
费米能级划分了电子能带中的占据和未
占据态，影响了电子的导电行为。
3
金属中的电子贡献
固态电子学
《固体中的电子》PPT课程涉及了固态物理学的概述、电子在固体中的行为 介绍、固体的电子能带结构、半导体和导体的区别、能带间隙、费米能级、 电子在能带中的分布等主题。课程还讨论了能带及其形状对电子的影响、金 属中的电子贡献、超导体的电子性质、材料的电阻率和导电性、电子与格子 的相互作用、电子散射、能带工程、量子点的电子性质、材料不同性质对电 子的影响、固态电子学的应用、电子学和信息技术以及未来的固态电子学发 展方向。
半导体和导体
半导体
半导体材料具有介于导体和绝缘体之间的导电性质， 广泛应用于电子器件中。
导体
导体材料具有良好的电流传导性能，常用于导线和 电路连接器等。
固态电子学应用
1 电子学和信息技术
2 量子点的电子性质
固态电子学是现代信息技 术的基础，推动了计算机、 通信和数据存储等领域的 发展。
量子点是一种特殊的固态 材料，具有优异的光学和 电学性质，可应用于光电 子器件和传感器。
3 材料的电阻电性，为材料设 计和应用提供重要依据。
未来的固态电子学发展方向
纳米材料
纳米材料的研究将推动材料性 能的突破和新型器件的发展。
低功耗
低功耗电子器件和电路的研发 是未来固态电子学的重要方向。
可扩展性

固体电子学PPT

固体电子学PPT

3 (2 ) ( a2 a3 ) [( a3 a1 ) ( a1 a2 )] * b1 (b2 b3 ) 3 3 (2 ) ( a2 a3 ) {[( a3 a1 ) a2 ]a1 [( a3 a1 ) a1 ]a2 } 3 =0 3 3 (2 ) ( a2 a3 ) a1 (2 ) 3
Rn n1a1 n2a2 n3a3
n1，n2，n3为包括零在内的任意整数 晶体中任一物理量沿基矢方向平移基矢的整数倍，保持性质不 变，体现了平移对称性。
2. 在波矢空间里——倒格子
晶体结构的周期性
Q r Q r Rl Rl —晶格格矢
a1 ( a 2 a 3 )
——原胞体积
倒格矢：倒格子中任一格点的位置矢量
11
2) 正、倒格子间的关系
I.
a i b j 2 ij
i , j 1, 2, 3
II. 倒格子原胞体积是正格子原胞体积的倒数的 (2 π ) 3倍。
简证： 倒格子原胞体积
电子在边长为L的立方体中自由运动——三维无限深势阱模型
0 V x, y, z
0 x, y, z L x, y, z 0或x, y, z L

2 2m
2 E
k 2 2mE 2
分离变量法：
2 2 2 2 2 2 y z x
c 0 1 0 c2 f H2 0 0 1 c H ff Ek f
上式是以系数 Ci 为未知数的一次齐次方程组， 它有非零解的条件是系数行列式为零

大学固体物理ppt课件

大学固体物理ppt课件
离子、电子在外场中的势能 e z e z ez
V r2单m2↓电V子2r体V系Rrn 6
周期势场中单电子态薛定谔方程：
V单电r子2的mV2 本r征2态RV波n 函r数
r
E r
单电子本征态能量
布洛赫电子：这种无相互作用并在周期性势场中
运动的电子！
7
二、Bloch 定理证明：布洛赫定理内容
当势场具有晶格周期性时,
k x a eika k x
21
k x a
k x
i cos3
a
x
若若若若若iieikkieekkkek只只只i只ekccciciii只kkkkkkkkcoaioaoaoakk取取取s取xsoaxssxaxa取s3x布3a布3a3a布布aaaaa1aa1a,1a1,3里布里,a,x里ax里xxa133渊a渊,3ia3里i渊渊acaixic区,co区,co3区,区s渊o,osa内i5内s5as3ac内35a内5a的区a3i,a的3oiaca的ci的s值iox值oxc内5cs：s值oax：3值ox3aas：s3aa的：iaaa3ac3aaxaxa值oxaikxsik：xccoik3oaiskcaascaaok3oak3saxasxaxxk3k3axaikxexc3xei若k3xoaikasiekkea3只keci3ikkkik3akxoaaax取sxkak2x32布xaax1,e里3
如果引入矢量:
k
l1 N1
b1
l2 N2
b2
l3 N3
b3
根据倒格子基矢的定义：（i,j = 1，2，3）
i j, ai .bj 0
i j, ai .bj 2
e n1 n2 n3 123
i k .Rn
e N1

《固体中的电子》课件

《固体中的电子》课件
纳米电子学
利用纳米材料和纳米结构制造电子器件，可以实现更小尺寸的集成 电路、更高的信息处理速度和更低的能耗。
纳米医学
利用纳米材料和纳米技术进行药物传递、诊断和治疗，可以提高药 物疗效、降低毒副作用，对医学领域产生深远影响。
THANKS
感谢观看
详细描述
当光子照射到物质表面时，光子的能 量被电子吸收，使电子获得足够的能 量逃离原子束缚，形成电流。光电效 应在太阳能电池、光电探测器等领域 有广泛应用。
热电效应
总结词
热电效应是指由于温度差异引起的电势差现象。
详细描述
当两种不同导体连接在一起时，在温度梯度的作用下，电子从高温端流向低温端，形成电势差。热电效应在温差 发电、测温等领域有重要应用。
用。
超导磁悬浮
利用超导材料的磁悬浮特性，实 现高速列车的无接触悬浮与导向， 具有高速、低能耗、无噪声等优
点。
超导储能
利用超导线圈储存磁场能量，可 以在需要时快速释放出来，用于 调节电网峰谷负载、稳定系统电
压等。
纳米技术
纳米材料
尺寸在纳米级别（1-100纳米）的材料，具有独特的物理化学性 质，在催化、传感器、医药等领域有广泛应用。
《固体中的电子》课件
• 电子与原子的关系 • 固体中的电子行为 • 电子在固体中的运动 • 固体中的电子效应 • 电子在固体中的应用
01
电子与原子的关系
电子的特性
电子是带负电的次原 子粒子，具有围绕原 子核运动的特性。
电子在原子中的运动 速度极快，约为光速 的十分之一。
电子的质量约为质子 质量的1/1836，其 数量决定了元素的化 学性质。
电子在原子中的位置
电子在原子中的位置是量子化 的，它们存在于特定的能级上。

第一章 固体中电子能量结构和状态 PPT

第一章 固体中电子能量结构和状态 PPT

1.2.1 金属中自由电子的能级
一维情况，建立一维势阱模型
U(0) U(L)
边界条件 U( x) 0,U(0) U(L)
U(x) 0
电子能量
0
L
E
h2
2m2
2 2m
K2
代入一维薛定谔方程
d
2 ( x)
dx2
2mE 2
(x)
0
d
2 ( x)
dx 2
(
2
)2
(
x)
0
解得 Acos 2 x B sin 2 x
▪金属的费密（Fermi）-索末菲（Sommerfel）
电子理论
▪晶体能带理论
内容先后基本按照人类对电子行为认识的逐渐深入
1.1 .1电子的粒子性
霍尔效应(Hall effect) B
以金属导体为例：
I
金属中的电流就是自由
E
++_++ +_ ++_ ++_+++ Nhomakorabea+
_
+ +
_
+ +
_
+ +
_
+ +
d 2 ( x)
dx2
4 2
h2
p2 ( x)
因 P2 2mE （非相对论形式，E为经典粒子动能）
d
2 ( x)
dx2
2mE 2
(
x)
0
此为一维条件下自由电子的薛定谔方程
如电子是不自由的，其总能量是势能和动能之合 P2 2m(E U )
d
2 ( x)

兰州大学固体物理第6章自由电子论ppt课件

兰州大学固体物理第6章自由电子论ppt课件

温度的变化很小。
总电子数：
N 0 D( )
f (.T ) dε=常数
（不随温度变化）
N T 0
F N 0 F D( )
f (.T ) dε=常数
即： F N T 0
或
0 F
D( )
f T
d 0
又
cel 0 D( )
f T
d
再加上一项等于零的积分对Cel无影响 则：
cel 0 D( )
sω
dsω Kω
相应的电子气的轨道密度的一般表达式为：
D(ε)
V 4π 3
sε
dsε k ε
(由于自旋×2)
总电子数与费米能的关系：
N
V
3
2
(
2m
2
F
3
)2
在波式空间中能量为的等能面所包围
的轨道数为：
N
V
3
2
(2m
3
2) 2
下面推导此式：
k
2m
2
在波矢空间，波矢为k的球的球体体积为：
4/3πk3，每个k值占的体积为(2π/L)3，每
2 z
)
=恒常
在波矢空间是一球面方程，不同能量的等 能面是一系列同心球面。
电子在T=0k时所能填充到的最高 等能面称为费米面，我们知道自由电 子的等能面是球面，在T=0k时，费米 面把电子填充过的轨道与电子未填充 过的轨道完全分开了，即费米面内所 有的轨道都被填充，费米面外边都是 空轨道，这一点对金属是非常主要的， 因为只有费米面附近的电子才能决定 金属的动力学性质。
电子气的轨道密度为抛物线关系，费米分 布函数为：
在T=0时，轨道全占满，但当温度T上升 时，费米面附近的电子可能激发到高轨道上 去，在温度T时能受热激发的电子数(只看到 数量级)大约为：（kBT/εF）N，则在温度T 时电子气热能的增加为：

电子与固体物质的作用ppt课件

电子与固体物质的作用ppt课件

单击此处编辑母版标题样式
五、相互作用的体积和信号产生 相的互深作用度体积和的形广状和度大小
➢电子与固体试样相互作用体积的 形状和大小与入射电子的能量、试 样原子序数和电子束入射方向有关。
➢对于轻元素，相互作用体积呈梨 状；对重元素试样，相互作用体积 呈半球状。
➢入射电子能量增加只改变相互作 用体积的大小，但基本形状基本不 变。
电子与固体物质的相互作用
单目击此录处编辑C母o版n标题t样e式nts
1 电子散射 2 内层电子激发后的弛豫过程 3 自由载流子 4 电子与固体作用产生的各种信号 5 相互作用体积与信号产生的深度和广度
单击此处编辑母版标题样式
一、电子散射
➢ 当一束聚焦电子束沿一定方向射入试样内，在原子库仑电 场作用下，入射电子方向改变，称为散射。原子对电子的散 射可分为弹性散射和非弹性散射。 ➢ 在弹性散射中，电子只改变方向，基本无能量的变化。 ➢ 在非弹性散射中，电子不但改变方向，能量也有不同程度 的减小，转变为热、光、X射线和二次电子等。 ➢ 原子对电子的散射具体分为：
➢用检测电流的方式可以得到吸收电子的信号像，它是背散 射电子像和二次电子像的负像。
➢现在一般不采用这种方式获得照片。
单击此处编辑母版标题样式
透射、吸收、背散射和二次电子之 间的强度关系
➢样品本身要保持电平衡，这
些电子信号必须满足以下关
系：
ip=ib+is+ia+it
式中：ip是入射电子强度；ib 是背散射电子强度；is是二次 电子强度；ia是吸收电子强度； it是透射电子强度。
子能量，且俄歇电子的平均自由程很小（ 1nm左右），只有表面1nm左 右范围内逸出的俄歇电子才具有分析意义。因此俄歇电子特别适合表面 层的成分分析。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
该能级称受主（acceptor）能级。
16
P型半导体
Si Si Si Si
Si Si
+ B
Si
价带
受主能级
Eg
满带
Ea
电子……少数载流子
17
3.半导体的电阻和温度的关系(p239)：
导体的电阻 随 温度升高而升高 R 半导体
半导体的电阻 随 温度升高而降低
金属
热敏电阻 T
4.半导体的光电导现象(p239)：
导体的能带结构 在外电场的作用下，大量共有化电子很 易获得能量，集体定向流动形成电流。
E E
导带
满带
E 空带 价带
从能级图上来看，是因为其 共有化电子很易从低能级跃 迁到高能级上去。
8
绝缘体能带结构
E 满带与空带之间 有一个较宽的禁带 （Eg 约3～6 eV）， 共有化电子很难从低 能级（满带）跃迁到 高能级（空带）上去。
满带上带正电的 空穴向下跃迁也 形成电流, 这称为空穴导电。
空带 Eg
满带
13
二. 杂质半导体 １. n型半导体 四价的本征半导体 Si、Ｇｅ等，掺入少量 五价的杂质（impurity）元素（如P、As 等）形成电子型半导体,称 n 型半导体。
掺杂后多余的电子的能级在禁带中紧靠 空带处, ED～10-2eV，极易形成电子导电。
(3)．空带（未排电子） 亦称导带
(4)．禁带（不能排电子）
5
E 3d
空带
3p
禁带
导带
3s
价带
2p
禁带
2s
满带
1s
6
2.导体,半导体和绝缘体 固体按导电性能的高低可以分为
导体
半导体
绝缘体
导体——电阻率 < 10-8 m
半导体——10-8 m < < 108 m 绝缘体—— > 108 m
7
电子吸收光子的能量：
光生载流子
内光电效应
18
29.6 Ｐ-Ｎ结
(1).Ｐ-Ｎ结的形成 p型
n型
p型半导体与n型半
导体的交界区。
由于Ｎ区的电子向Ｐ区 扩散，Ｐ区的空穴向Ｎ
E阻
区扩散，在ｐ型半导体
和Ｎ型半导体的交界面
附近产生了一个电偶层
称之 为阻挡层 (厚度 约1m, 场强约106~108V/m）。
类本征半导体，在上述方法中能激发其传导电
子的只有
（A）（1）和（2） （B）（3）和（4）
（C）（1）（2）和（3）
(D)
（D）（1）（2）和（4）
例8:已知T=0K时锗的禁带宽度为 0.78ev ，则
锗能吸收的辐射的最长波长是
m
解：设锗 Eg
max
hc Eg max
max hc / Eg 1.59106 m 1.59m 26
反向
称为漏电流
（Ａ级）。
I（微安）
V(伏)
-１０ -２０ -３０
当外电场很强,反向电压超过某一数值后， 反向电流会急剧增大----反向击穿。
p180
23
伏安特性：
I
o
U
应用：整流(rectification)
24
例5: 若硅用锑（5价元素）掺杂，则成为 n
型半导体，请在所附的能带图中定性画出施主
该能级称为施主（donor）能级。
14
n 型半导体 Si Si Si Si
Si P
Si Si
价带
ED
施主能级 Eg
满带
空穴……少数载流子
15
２.ｐ型半导体 四价的本征半导体Si、Ｇe等，掺入少量 三价的杂质元素（如Ｂ、Ga、Ｉn等） 形成空穴型半导体，称 p 型半导体。
掺杂后多余的空穴的能级在禁带中紧靠 满带处，ED～10-2eV，极易产生空穴导电。
例9: 下述说法中，正确的是
s能带：2N个量子态
p能级：6个量子态
p能带：6N个量子态
⒈电子对能带的填充 固体中的一个电子只能处在某个能带中的 某一量子态上。
4
填充原则：
(１). 服从泡里不相容原理 (２). 服从能量最小原理 有关能带被占据情况的几个名词： ( 1)．满带（排满电子）
(2)．价带（能带中一部分能级排满电子） 亦称导带
能级或受主能级。
导带（价带）
•施主• 能• 级• •
禁带
满带
导带（价带）
禁带 受主能级
• ••••
满带
例6: 若锗用硼（三价元素）掺杂，则成为p
型半导体，请在所附的能带图中定性画出施主
能级或受主能级
25
例7: 激发本征半导体中传导电子的几种方法有
（1）热激发（2）光激发（3）用三价元素掺
杂（4）用五价元素掺杂，对于纯锗和纯硅这
导带 禁带 Eg 满带
半导体能带结构: 满带与空带之间也是禁带， 但是禁带很窄（E g 约0.1～2 eV )。
9
3.绝缘体与半导体的击穿
当外电场非常强时，电子还是 能越过禁带跃迁到上面的空带中。
绝缘体 半导体导体来自1029.5 半导体的导电机构 一. 本征半导体（semiconductor）
本征半导体是指纯净的半导体。 1. 电子导电……半导体的载流子是电子
I （毫安）
３０
正向
２０
１０
0
0.2
V（伏）
1.0
21
b. 反向偏压
在Ｐ-Ｎ结的ｐ型区接电源负极,
叫反向偏压。
E
阻挡层势垒增
p型
n型
E阻
I 大、变宽，不 利于空穴向Ｎ
区运动，也不 利于电子向P 区运动,没有正
向电流。
22
但是，由于少数 载流子的存在， 会形成很弱的反 向电流，
击穿电压
-30 -20
P-N结
19
(2). Ｐ-Ｎ结的单向导电性 a. 正向偏压
在Ｐ-Ｎ结 I 的p型区接
p型
电源正极，
叫正向偏压。
E
n型
E阻
阻挡层势垒被削弱、变窄，有利于空穴
向N区运动，电子向P区运动， 形成正向电流（mＡ级）。
20
外加正向电压越大， 正向电流也越大， 而且是呈非线性的
按指数规律增长。
伏安特性(图为锗管)。
2. 空穴导电……半导体的载流子是空穴 空穴: 满带上的一个电子跃迁到空带后,
满带中出现一个空位。 本征半导体包含电子导电和空穴导电两种形式.
11
空带
h
Eg=2.42eV
满带
这相当于产生了一个带正电的粒子 (称为“空穴”) 。
电子和空穴总是成对出现的。
12
在外电场作用下,
空穴下面能级上 的电子可以跃迁 到空穴上来, 这相当于空穴 向下跃迁。
第29章 固体中的电子 29.4 能带 导体和绝缘体
晶体 固体 准晶体
非晶体
1
晶体的周期性势能函数:
U
U
.+ r
.+ .+ r
(a) U
(b)
.+ .+ .+ .+ r E2
E1
(c)
2
晶体的特点： 周期性结构 周期性势能函数 原子的能级 分裂成晶体的能带P174
e.g. 2p
2s
1s
3
Note: 若孤立原子某一能级包含k个量子态, 则由 N个原子周期性排列形成固体后, 该能级分 裂成的能带包含kN个量子态. e.g. s能级：2个量子态