d dt
3
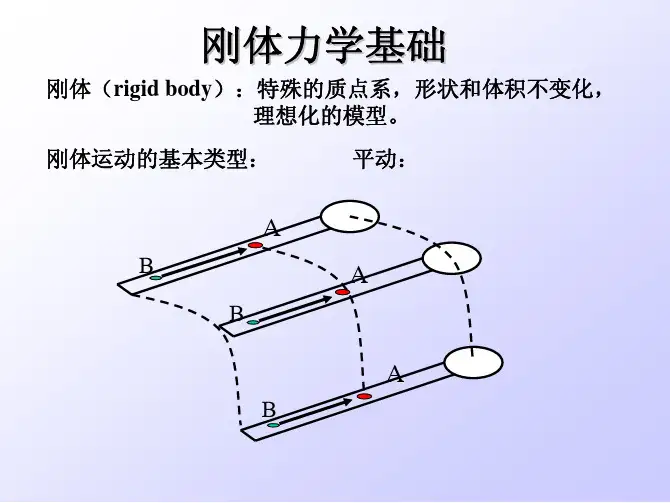
二. 刚体的定轴转动 1.力矩
力F 对o点的力矩定义为:
M=r×F 力矩的大小: M=Frsin =Fd 方向: r F 右手螺旋 注意: 对定轴转动, (1)只有 在垂直于转轴平面内的力才会 产生力矩; 平行于转轴的力是 不会产生力矩的。 (2)力矩的方向沿转轴。
2
T2
m: mg-T2= ma
a=R1= r2 , 2=2ah
求解联立方程,代入数据,可得
m mg
=2m/s, T1=50N, T2=60N。
17
例题1.6 均匀细棒(m、长l)AB可绕o轴转 动,Ao= l/3。求棒从水平位置静止开始转过 角 时的角加速度和角速度。 解 重力集中在质心,其力矩为
即一对内力的力矩的矢量和为零。 也可以从力矩大小对应于平行四边形面积的角 度来看。 两个平行四边形底和高都相等,故而面积相同; 两力矩大小相等,方向相反,于是矢量和为零。 任意质点系的合内力矩都为零。
6
三. 转动惯量
1.转动惯量的物理意义
M I F ma
质量m—物体平动惯性大小的量度。
2
1
2
t1
26
例题2.1 一质点的质量为m,位矢为: r =acos t i+bsin t j (式中a、b、 均为常量); 求质点的角动量及它所受的力矩。 z dr k 解 asinti bcostj j o dt
i x L r ( m ) mr m(acosti bsintj ) ( asinti bcostj ) 2 2 mabsin tk mabcos tk
25