三年级下册数学课件中国古代数学家杨辉西师大版

(a+b)6…1 6 15 20 15 6 1
观察每一行的第一个和最后一个数有什么特点？
(1)对称性: Cn0 1,Cnn 1
与首末两端“等距离”的两个二项式系数相等．
这就是组合数的性质
1: Cnm
C nm n
第2页/共32页
(a性+b质)1…………… 1 1
(2)递推性:
除(a1+以b)外2…的…每…一个…数…都1等2于它1肩上两个数的和.
第15页/共32页
题型 证明不等式
例20．证明： 当n N*且n 1 2 (1 1)n 3
n
证明 (1
1 )n n
1 Cn1
1 n
Cn2
1 n2
11 Cn2
1 n2
2
通项
Cnk
1 nk
n(n
1)
k
(n !
k
1)
1 nk
nk k!
1 nk
1 k!
(1
1)n n
1
C
1 n
1 n
Cn2
1，1，2，3，5，8，13，21，34，．．．
第21页/共32页
探究：横行规律
第0行
1 2 3
4 5 6 7
8 9 10 11 12 13 14
15
1）杨辉三角中的第1，3，7，15，…行，即第 2n-1行的 各个数字为奇数？
则第2n行的数字有什么特点？除两端的1之外都是偶数.
第22页/共32页
解:?1二项式系数之和为C90 C91 C92 C99 29 512.
解 : 设2x 3y9 a0x9 a1x8y a2x7y2 a9y9. 2令x y 1得各项系数之和为a0 a1 a2 a9 21 319 1.

我国南宋数学家杨辉用三角形二项和的乘方规律
杨辉1984年出生于西南地区的一个普通家庭，拥有着雄厚的数学天赋，14岁时便成功解决了几何学中普通三角形的库伦算法。

后来，他发展了一种普遍有效的数学方法-三角形二项和的乘方规律，为我国数学家研究发展提供了重要参考。

杨辉的研究历时10多年，他的乘方规律也被称为“杨辉定理”，该算法是数学界一个非常重要的理论发现，并据此研究丰富完善了四角形的报色算法。

三角形二项和的乘方规律即杨辉定理，是指一个等腰三角形的两个斜边的平方和等于其底边的平方。

杨辉定理的推导依赖多边形解析几何学上的基本知识，是一种知识和技术性比较强的数学原理，早在古代就已有诸多学者提出这一原理，杨辉定理是这些研究的综合，它比其他的原理更加完善，系统，更加准确的描述了几何知识。

三角形二项和的乘方规律广泛应用于众多学科，并助力科研。

从计算机科学、物理学到心理学，杨辉定理都发挥着无可取代的作用。

以物理学研究为例，三角形二项和的乘方规律可以用于研究光传播系统，指导显微镜、太阳能镜和其他光学仪器的设计，有效改善用于测量距离、角度、角动量等的几何精度。

杨辉用三角形二项和的乘方规律的研究，无疑推进了我国的数学发展，为全球数学界发展做出了重要贡献。

西师大版三年级数学下册电子课本目录(义务教育教科书)_
－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－
一两位数乘两位数的乘法
两位数乘两位数
你知道吗中国古代数学家杨辉
二长方形和正方形的面积
面积和面积单位
长方形和正方形面积的计算
面积单位的换算
三三位数除以一位数的除法
三位数除以一位数
四旋转、平移和轴对称
旋转与平移现象
初步认识轴对称图形
你知道吗建筑中的对称
五小数的初步认识
小数的初步认识
一位小数的加减法
你知道吗小数点的由来
六简单的统计活动
综合与实践一天用的纸
七总复习
感谢阅读，欢迎大家下载使用！。

又因为p>k且p为素数, 所以 c p 中一定含有因数p，故p整除 第p行中除数1外的所有数。
k
小结
1、第2k-1行（k是正整数）的各个数字均为奇数
2、如果p是素数，那么在第p行中，除去两端的 数字1外，行数p整除其余的所有的数。 3、各行数字的和均为2n（n是行数）。 4、第2k-1行的所有数Байду номын сангаас为奇数，第2k行的所有 数都是偶数（除两端的1外）k是正整数。
杨 辉
杨辉三角
题引
杨辉，字谦光，南宋末钱塘人。作过地方官员， 曾被赞为“以廉饬己，以儒铈吏；吐胸中之灵气，继前 贤之奥旨”。他是宋代甚至也是中国古代最杰出的数学 教育家，十分重视数学教育和普及工作。1261年他所著 的《详解九章算法》里，记载着类似下面的表：此表称 为杨辉三角。 杨辉三角是我国古代数学 一 的研究成果之一，它的发 现比法国数学家帕斯卡早 一 一 500年左右。它和勾股定理、 一 二 一 圆周率的计算等其他中国 古代数学成就，一并显示 一 三 三 一 了我国古代劳动人民的卓 一 四 六 四 一 越智慧和才能。
一 五 十 十 五 一
杨 辉 三 角 ——
一
六
十五
二十 十五 六
一
杨辉三角之雾里看花
1、与二项式定理的关系：
表中的每个数都是组合数， r Cn 第n行的第r+1个数是 第n行是二项式展开式的系数 列
2、对称性：
r n
尝 ，即 表中的数字左右对称 C 试 C 对称轴是杨辉三角底 探 边上的高。 索
n r n
3、结构特征：
Cnr Cnr11 Cnr1 除底边上1以外的各数，都等于它肩上的两数之和，即
探索
试证明：杨辉三角中，若行数p是素数，则p 整除第p行中除1以外的所有数。 证明：在第p行中除去数1外的所有数 k 可用 c p 表示(0<k<p且k为整数)

3、毕达哥拉斯[古希腊]
毕达哥拉斯（公元前572—公 元前497）古希腊数学家、哲 学家。无论是解说外在物质世 界，还是描写内在精神世界， 都不能没有数学！最早悟出万 事万物背后都有数的法则在起 作用的，影响西方乃至世界的 人物第一个着重“数”的人毕 达哥拉斯定理证明了正多面体 的个数，建设了许多较有影响 的社团毕达哥拉斯学派，“西 19 方的勾股定理”之父。
30命名以示纪念。
15、爱因斯坦[美国]
阿尔伯特·爱因斯坦，美籍德国犹太裔， 理论物理学家，相对论的创立者，现 代物理学奠基人。1921年获诺贝尔物 理学奖，1999年被美国《时代周刊》 评选为“世纪伟人”。 阿尔伯特·爱因斯坦，世界十大杰出物 理学家之一，现代物理学的开创者、 集大成者和奠基人，同时也是一位著 名的思想家和哲学家。1933年爱因斯 坦在英国期间，被格拉斯哥大学授予 荣誉法学博士学位。因受纳粹政权迫 害，迁居美国，任普林斯顿高级研究 所教授。从事理论物理研究，1940年
9 用另一种方法证明。
8、刘徽
刘徽（约公元225—295），山东邹平县 人，魏晋期间伟大的数学家，中国古典 数学理论的奠基者之一。是中国数学史 上一个非常伟大的数学家，他的杰作 《九章算术注》和《海岛算经》，是中 国最宝贵的数学遗产。刘徽思想敏捷， 方法灵活，既提倡推理又主张直观．他 是中国最早明确主张用逻辑推理的方式 来论证数学命题的人．刘徽的一生是为 数学刻苦探求的一生．他虽然地位低下， 但人格高尚．他不是沽名钓誉的庸人， 而是学而不厌的伟人，他给我们中华民 族留下了宝贵的财富。
刘徽思想敏捷方法灵活既提倡推理又主张直观他是中国最早明确主张用逻辑推理的方式来论证数学命题的人刘徽的一生是为数学刻苦探求的一生他虽然地位低下但人格高尚他不是沽名钓誉的庸人而是学而不厌的伟人他给我们中华民族留下了宝贵的财富

• 这实际是201到300的全部素数．虽然杨辉 对素数的研究远在欧几里得之后，理论上 也不够完整，但他在没有外来影响的情况 下注意到这一重要问题，其思想之深刻是 值得称道的． • “求一乘”和“求一除”也是捷算法， 是用加减代乘除，通过折、倍等方法来实 现的，“求一”就是变首位为1的意思．例 如237，他说：“夫 习算者，以乘法为主．”(《详解九章算法》) 认为“乘除者，本勾深致远之法”，“因法不 独能乘，而亦能除”(《算法通变本末》)．例 如 • 2746÷25=27.46×4=109.84， • 这种以乘代除的方法不仅施于精确计算， 也用于近似计算．例如 • 2746÷1111=0.2746×9=2.4714． • 《田亩比类乘除捷法》中的一些题列出了 不同的方法，这些方法有繁有简，杨辉的意图 就在于比较优劣，提倡捷法．
•
由于捷算法的需要，杨辉注意到一个整数是 合数还是素数的问题．他说：“置价钱(即 23121文)为法，约之．先以九约，又以七约， 乃见三百六十七，更不可约也．”所谓不可约， 就是说除了1和本身外没有其他约数．显然， 杨辉的“不可约”之数即素数．他在这里首次 提出素数概念，又在《法算取用本末》中列出 了从201到300的素数表，共16个： • 211，223，227，229，233，239，241，251， • 257，263，269，271，277，281，283，293．
• 就在这种数字神秘主义气氛笼罩社会的时 候，杨辉却在孜孜不倦地探索纵横图的构 成规律。他以自己的研究成果，否定了纵 横图的神秘性．《续古摘奇算法》上卷的 大量纵横图表明，这种图形是有规律可循 的． • 杨辉首先给出三阶和四阶纵横图的构 造方法：“易换术曰，以十六子依次第作 四行排列，先以外四角对换……后以内四角 对换．”这便是构造四阶纵横图的一种方 法(图2)．在“总术”中，杨辉给出构造四 阶纵横图的一般方法．第一步是“求积”， 即求出每行或每列的数字之和应为多少．

我国南宋数学家杨辉三角形解释二项和的乘方规律
杨辉三角形是中国古代数学中著名的图形。

它是由数列构成的一个三角形，其中每个数字等于它上方的两个数字之和。

数学家杨辉在南宋时期发现了这个特殊的数列，因此得名杨辉三角形。

杨辉三角形不仅仅是一个有趣的数学现象，而且还有很多实际的应用。

其中一个重要的应用就是解释二项式系数的乘方规律。

二项式系数是指在二项式展开式中，某一项的系数，例如(a+b)^3展开后，其中的a^2b的系数为3。

这个系数可以用杨辉三角形来解释。

首先，我们可以将二项式(a+b)^n展开为
(a+b)(a+b)(a+b)...(a+b)的形式，其中有n个(a+b)相乘。

然后，我们可以将每个(a+b)展开成两个数a和b，并将它们排列在杨辉三角形的下一行。

对于第一行，我们将a和b排列在两端，然后在它们中间加上一个0，表示这一行的数字总数为3。

接着，我们通过依次将上一行的相邻数字相加得到下一行的数字，直到得到第n+1行为止。

这个构造的过程可以用图示表示。

例如，当n=3时，我们可以得到以下的杨辉三角形：
1
1 1
1 2 1
1 3 3 1
在这个杨辉三角形中，第n+1行的数字对应着二项式系数中的系
数。

例如，对于(a+b)^3展开式中的a^2b项，它的系数为3，对应着杨辉三角形的第四行中的数字3。

通过这种方法，我们可以很容易地求出任意二项式系数的值。

这不仅为数学家们提供了一个有用的工具，而且也让人们更好地理解了杨辉三角形这个有趣的数学现象。

根据规
ห้องสมุดไป่ตู้
律填数
练一练 1
34
13 21
5 8 13
2358
11235
练一练 2
2
4
3
6
9
4
8
12
16
5 10 15
20
25
6
12 18 24 30 36
探索规律的方法：
一看： 一看：看清题目里的信息。
二想：对信息进行分析、比较 或运用计算等方法去寻找规律。
三说：用简洁的数学语言去 归纳、总结、描述规律。
1
5
10 10
5
1
规律1：每行首尾的数都是1. 规律2：每行中间各数都是前一行左右两个数的和.
3 怎样填？
11 121 1331 14641 1 5 10 10 5 1
1 6 15 20 15 6 1
教科书64页 根据规律在圆圈中填数
2
2
2
6
2
4
2
6
2
2
2 2
10 8
20 12
20
8 10
2 2
谢谢观赏
You made my day!
我们，还在路上……
•不习惯读书进修的人，常会自满于现状，觉得再没有什么事情需要学习，于是他们不进则退。经验丰富的人读书用两只眼睛，一只眼睛看到纸面上的话，另 一眼睛看到纸的背面。2022年4月10日星期日2022/4/102022/4/102022/4/10 •书籍是屹立在时间的汪洋大海中的灯塔。2022年4月2022/4/102022/4/102022/4/104/10/2022 •正确的略读可使人用很少的时间接触大量的文献，并挑选出有意义的部分。2022/4/102022/4/10April 10, 2022 •书籍是屹立在时间的汪洋大海中的灯塔。

“杨辉三角”比 西方的“帕斯卡三 角”早出现300多年。
找规律填数
1 11 1 21 1331 14641 1 （） （）（） （） 1
1 22 3 43 47 7 4 5 （） （）（） 5
通过这节课的学习， 你有什么收获？
两条斜边都是由数字1组成，其余的数则是 等于上一行左右两个数字之和。
每行数字左右对称，由1开始逐渐变大，然 后变小，最后再回到1。
每一行的数字个数与行数同样多。
杨辉是南宋时期杭州人，在他1261年所著书中， 记录了如图所示的三角形数表，这三角形就被称为杨 辉三角。在欧洲直到1623年以后，法国数学家帕斯卡 才发现了同样的规律，因此欧洲人又称这个三角“帕 斯卡三角”。但是大家从杨辉发现这 个规律的年代与帕斯卡发现这个规律 年代相比就会知道，我国的杨辉发现 此规律比帕斯卡早了300多年。近年 来国外也逐渐承认这项成果属于中国， 开始称这个三角为“中国三角的数学家，与 秦九韶、李治、朱世杰一起 被誉为“宋元数学四大家”。
杨辉一生写了很多 数学著作,流传很广, 朝鲜、日本等国均有译 本出版。
杨辉为初学者制 定的“习算纲目”， 集中体现了他的数学 教育思想和方法。
杨辉在计算方面很有 研究，“杨辉三角”为其 代表作，具有很大的实 用价值。

杨辉三角简介
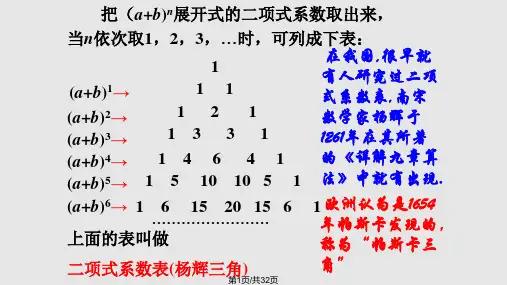
中国古代数学家在数学的许多重要领域中处于遥遥领先的地位、中国古代数学史曾经有自己光辉灿烂的篇章，而杨辉三角的发明确实是十分精彩的一页、杨辉，字谦光，北宋时期杭州人、在他1261年所著的《详解九章算法》一书中，辑录了如下所示的三角形数表，称之为“开方作法本源”图、
上图表示的是两个未知数和的幂次方运算后的系数问题，比如〔x＋y〕＝x2＋2xy＋y2，如此系数确实是1、2、1，这确实是上图中的1行、立方，4次方，n次方的运算只要看看上图中的各项的系数，就特别容易得到结果、上图确实是杨辉三角，也叫贾宪三角，在外国被称为帕斯卡三角、它与我们现在的学习联系最紧密的是2项式乘方展开式的系数规律、
杨辉三角最本质的特征是：它的两条斜边基本上由数字1组成的，而其余的数那么是等于它肩上的两个数之和、。

数学家杨辉三角的故事
杨辉三角，也被称为贾宪三角或帕斯卡三角形，是二项式系数在三角形中的一种几何排列。

在中国古代，数学家杨辉在南宋时期（1261年）的著作《详解九章算法》中首次描绘了这一三角形，并称之为“开方作法本源”图。

在欧洲，法国数学家帕斯卡在1654年也发现了这一规律，因此这个表在欧洲也被叫做帕斯卡三角形。

杨辉三角的发现是中国古代数学的杰出研究成果之一。

这个三角形把二项式系数图形化，把组合数内在的一些代数性质直观地从图形中体现出来，是一种离散型的数与形的优美结合。

杨辉三角的每个数等于它上方两数之和，这一性质使得其在数学中有着广泛的应用。

例如，在组合数学中，杨辉三角可以用来计算组合数；在代数中，它可以用来展开二项式；在概率论中，它可以用来计算某些事件的概率等。

此外，杨辉三角还与一些数学游戏和问题有关，如“堆垛术”问题、纵横路线图问题等。

这些问题都可以通过杨辉三角来找到解决方案。

总之，杨辉三角是一个在数学中有着广泛应用和深远影响的数学概念，它的发现和应用展示了中国古代数学的卓越成就和独特魅力。

古代数学家杨辉的故事
宋、元数学四大家之一的杨辉是世界上第一个排出丰富的纵横图和讨论构成规律的数学家．
说起杨辉的这一成就，还得从一件偶然的小事说起．一天台州府的地方官杨辉坐轿出外巡游，半路上被一个在路中间算题的孩童拦住道路不能通过．杨辉一看来了兴趣，连忙下轿，抬步来到前面．
杨辉摸着孩童的头说：“为何不让本官从此经过？”
孩童答道：“不是不让经过，我是怕你们把我的算式踩掉，我又想不起来了．”
“什么算式？”
“就是把1到9九个数字分三行排列，不论直着加、横着加还是斜着加，结果都是等于15．我们先生说下午一定要把这道题做好．我正算到关键之处．”
杨辉连忙蹲下身，仔细地看孩童的算式，觉得这个算式在哪儿见过，仔细一想，原来是西汉学者戴德编纂的《大戴礼》中所写的文章中提及的．杨辉和孩童两人连忙一起运算起来,直到天过午，两人才舒了一口气，结果出来了，他们又验算了一下，结果全是15，这才站了起来．结果如图1所示：
杨辉回到家中反复琢磨，一有空闲就在桌上摆弄这些数字，终于发现了其中的规律，按照类似的规律，杨辉又得到了“花16图”——把从1到16的数字排列在四行四列的方格中，使每一横行、纵行、斜行四数之和均为34．后来，杨辉又将散见于前人著作和流传于民间的有关这类问题加以整理，得到了“五五图”“六六图”“衍数图”“易数图”“九九图”“百子图”等许多类似的图．杨辉把这些图总称为纵横图，于1275年写进自己的数学著作《续古
摘奇算法》一书中，并流传后世．
但长期以来，人们习惯于把它当做纯粹的数学游戏，并没有给予应有的重视．随着近代组合数学的发展，纵横图显示了越来越强大的生命力，在图论、组合分析、对策论、计算机科学领域中都找到了用武之地．。

古老的杨辉三角， 即使在我们现代生活中 也能得到充分的利用， 我们中国人的祖先在几 百年前就能最先发现这 个有用的规律，是不是 令我们由衷地为我们中 国灿烂的古代文明心生 自豪之情呢？
6
7
2
杨辉三角的规律
杨辉三角的主要特征是：
1.两条斜边都是由数字1组成，其余的数则是等于上一行左右两个数字之和. 2.每行数字左右对称，由1开始逐渐变大，然后变小，最后再回到1. 3.第n行的数字个数为n个。 4.n行中第i个数是斜行i-1中前n-1个数之和。
杨辉三角计算演示
3
杨辉三角的应用 Ⅰ
杨辉三角可以用来帮助解决11的几次方的问题
杨辉三角
Chinese triangle
四年级（4）班
1
什么是杨辉三角？
杨辉是南宋时期杭州人。在
他1261年所著书中，记录了右边图所 示的三角形数表，这三角形就被称为 杨辉三角。在欧洲直到1623年以后， 法国数学家帕斯卡才发现了同样规律， 因此欧洲人又称这个三角为“帕斯卡三 角”。但是大家从杨辉发现这个规律的 年代与帕斯卡发现这个规律年代相比 就会知道，我国的杨辉发现此规律比 帕斯卡早了300多年。近年来国外也逐 渐承认这项成果属于中国，开始称这 个三角是“中国三角形”。（Chinese triangle）。好是杨辉三角所
对应的第n行的数字，很神奇吧！
4
杨辉三角的应用 Ⅱ
大家请看一下下面的表格能发现什么吗？
对，这就是杨辉三角的又一个应用： 2的n次方也就是第 n行数字之和，很有意思对吧？
5
概括
杨辉三角除了以上两个应用，我
们还可以在日常生活中来用它来计算最近的 路径问题以及弹子游戏中弹子掉落的概率等 许多问题。

1、学生认真倾听。
合作探讨
探索新知
1、出示数列，请学生观察这些数的排列，找找其中的规律，再和同桌的同学交流自己的。
生1：每排左、右两边的数都是1，只有中间的数在发生变化。
生2：每排都比它前一排多一个数。
生3：从第一排的1斜起看，依次是1、2、3、4……
第四课时
教学内容
教材P21。
教学目标
1、能从数的排列中去发现隐含的规律，并能应用规律。
2、能用自己的语言表述发现规律的方法。
3、陪躺学生独立思考、主动探索的精神及与同伴积极合作的意识。
教学重点
发现规律，能运用规律。
教具准备
课件。
教学过程
教师活动
学生活动
故事引入
教师：我国南宋末年出现了一位著名的数学家，他就是杨辉。他在数学方面取得了许多成就，其中计算技术方面的成就最突出，著名的“杨辉三角”对人类数学研究作出了贡献。今天我们要发现的规律就与“杨辉三角”有关（课件出示例题）
1、学生先独立观察，再小组合作讨论。
2、全班交流汇报。
巩固提高
生4：每排中间的数都等于前一排左、右两个数的和。
师：同学们观察得真仔细，有了这么多新发现，每排的第一个数都是1，中间的数都是它前一排左、右两个数的和等等，找到了这些规律，你们能知道第5排该填哪些数吗？试一试。再填出第6、7排各数。按这样的规律再往下面填，还会填吗？各数是按一定规律排列的，只要我们找到了事物内部隐藏的规律，就能正确地天出未知的各数。

876÷4= 406÷2= 615÷3=
219（m） 203（m） 205（m）
219＞205＞203
答：我会选杨欣，因为他跑得最快。
课堂练习
614÷2= 728÷7= 981÷9=
课堂总结
说一说怎样计算三位数除以一位数？
巩固练习
先找出错在哪里，再改正。
2
34 608
×
205 ×
2 502
201 ×
三年级下册第三单元
三位数除以一位数
第5课时
课件设计：李 洁 重庆市沙坪坝区树人景瑞小学
课堂引入
不计算，直接判断商是几位数。
279÷3 521÷4 740÷5
课堂引入
学校要进行 “跑步”，为了选拔出参加比赛第一名，体育老师测试了几个学 生跳绳的情况：杨欣4分钟跑了876m，李红2分钟跑了406m，刘星3分钟跑了615m。 如果让你来评选跳绳冠军，你会选谁？为什么？
课堂探索
李红：
406÷2= 203（m）
哪种写法更简便？
203
2 406 4 0 0 6 6 0
203
2 406 4 6 6 0
课堂探索
刘星：
615÷3= 205（m）
十位上的0能不能不写， 为什么？
205
3 615 6 1 0 15 15 0
2 05
3 615 6 15 15 0
杨欣： 李红： 刘星：
学习要求：
1.独立完成：想一想应该怎样计算，试着算一算谁跑得最快？ 2.小组合作：小组内说一说你是怎样计算的？在计算时你遇到了什么困难，你是怎样解 决的？ 3.汇报展示。
课堂探索
杨欣：
876÷4=
要知道谁跑得最快，必须先 算出他们一分钟能跑多少米？

一开始将九个数字从大到小斜排三行然后将9和1对换左边7和右边3对换最后将位于四角的4268分别向外移动排成纵横三行就构成了九宫图
数学家的故事
——杨辉
杨辉简介
杨辉，南宋杰出的数学家和 教育家。
他在总结民间乘除捷算法、 “垛积术”、纵横图以及数学教 育方面，均做出了重大的贡献。 他是世界上第一个排出丰富的纵 横图和讨论其构成规律的数学家。
杨辉与秦九韶、李冶、朱世 杰并称“宋元数学四大家”。
2
杨辉三角
杨辉三角，是二项式系数在三 角形中的一种几何排列，在中国南 宋数学家杨辉1261年所著的《详解 九章算法》一书中出现。
前提：每行端点与结尾的数为1.
1.每个数等于它上方两数之和。 2.每行数字左右对称，由1开始逐渐变大。 3.第n行的数字有n项。
4.第n行数字和为2n-1。
3
杨辉的故事
一天，台地方官杨辉出外巡游，前面 传来孩童的大声喊叫声，恶狠狠的训斥声。 差人来报：“孩童不让过，说等他把题目 算完后才让走，要不就绕道。”
杨辉说：“为何不让本官从此处经 过？”
孩童答道：“不是不让经过，我是怕 你们把我的算式踩掉，我又想不起来了。”
“什么算式？”
“就是把1到9的数字分三行排列，不 论直着加，横着加，还是斜着加，结果都 是等于15。我们先生让我们下午一定要把 这道题做好。我正算到关键之处。”
4
比较
杨辉连忙蹲下身，连忙一起算了起来，直到天已过午，俩人 才舒了一口气，结果出来了。
杨辉回到家中，反复琢磨，终于发现了其中的规律。他把这 条规律总结成四句话：九子斜排，上下对易，左右相更，四维挺 出”。就是说：一开始将九个数字从大到小斜排三行，然后将9 和1对换，左边7和右边3对换，最后将位于四角的4、2、6、8分 别向外移动，排成纵横三行，就构成了九宫图。

“杨辉三角”出现在杨辉 编著的《详解九章算法》一 书中，且我国北宋数学家贾 宪（约公元11世纪）已经用 过它，这表明我国发现这个 表不晚于11世纪．在欧洲， 这个表被认为是法国数学家 物理学家帕斯卡首先发现的, 他们把这个表叫做帕斯卡三 角．杨辉三角的发现要比欧 洲早500年左右.
杨辉三角基本性质
1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 1 8 28 56 70 56 28 8 1 1 9 36 84 126 126 84 36 9 1 ………………………………
1
1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 1 8 28 56 70 56 28 8 1 1 9 36 84 126 126 84 36 9 1 ………………………………
我们不妨拿新出生的一对小兔子分析一下： 第一个月小兔子没有繁殖能力，所以还是一对； 两个月后，生下一对小兔民数共有两对； 三个月以后，老兔子又生下一对，因为小兔子还没有繁殖 能力，所以一共是三对；
第2k行的数字特征
所有数的和是偶数
1
1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 1 8 28 56 70 56 28 8 1 1 9 36 84 126 126 84 36 9 1 ………………………………
斐波那契数与植物花瓣 3……百合和蝴蝶花
5…蓝花耧斗菜、金凤花、飞燕草、毛茛花