三种统计图的特点

统计图的选择说课稿一、引言统计图是一种用来展示和比较数据的可视化工具，它可以匡助人们更好地理解和分析数据。

在教学中，选择合适的统计图对于匡助学生理解和记忆数据是非常重要的。

本说课稿将介绍在教学中如何选择合适的统计图，并通过实际案例进行说明。

二、统计图的种类常见的统计图包括柱状图、折线图、饼图、散点图等。

每种统计图都有其适合的场景和特点。

1. 柱状图柱状图适合于比较不同类别或者不同时间点的数据。

它通过不同长度的柱子来表示数据的大小，可以清晰地展示数据之间的差异。

例如，我们可以使用柱状图来比较不同城市的人口数量。

2. 折线图折线图适合于展示数据随时间变化的趋势。

它通过连接数据点的线条来表示数据的变化情况，可以匡助学生观察和分析数据的变化规律。

例如，我们可以使用折线图来展示某个城市每年的平均气温变化。

3. 饼图饼图适合于展示不同部份占整体的比例关系。

它通过不同大小的扇形来表示数据的比例，可以直观地展示各部份的重要性。

例如，我们可以使用饼图来展示某个班级不同学科的成绩比例。

4. 散点图散点图适合于展示两个变量之间的关系。

它通过扩散在坐标系中的点来表示两个变量的取值，可以匡助学生观察和分析两个变量之间的相关性。

例如，我们可以使用散点图来展示身高和体重之间的关系。

三、选择统计图的原则在选择统计图时，我们应该根据数据的特点和目的来进行选择。

以下是选择统计图的几个原则：1. 数据类型首先，我们需要考虑数据的类型。

如果数据是离散的，即只能取某些特定值，那末柱状图或者饼图可能更合适。

如果数据是连续的，即可以取任意值，那末折线图或者散点图可能更适合。

2. 数据关系其次，我们需要考虑数据之间的关系。

如果我们想要比较不同类别或者不同时间点的数据，那末柱状图或者折线图可能更适合。

如果我们想要展示数据的比例关系，那末饼图可能更合适。

如果我们想要展示两个变量之间的关系，那末散点图可能更适合。

3. 数据数量最后，我们需要考虑数据的数量。

本 题 设 计 别 具
匠 心 ， 颖 独 到 ． 要 考 察 了对 条 新 主 形 统 计 图 的 识 别 、 解 和 推 理 能 理 力． 条形 统 计 图 中 ， 们 可 以直 从 我
人 捐 了 ３册 书 ， ４人 捐 了 ４册 有
，
４
接 看 出 ： ２人 捐 了 １册 书 ， ４ ２ 有 有
缦 解 （ ６，； ）０３ １ ０４（ ２ ； ） ２ ０
６（ Ｏ １＋ ）＝ ０ ２ ＝ ． ，解 之 得 ＝ ７ ． ＝７ ＝ ％ ：１ 所 以 ２０ ０ ５年 的 绿 地 面 积 的 年 增 长 率 为 １ ． ７ 分析
图２
（ ）设 ２ ０ ３ ０ ５年 绿 地 面 积 的 年 增 长 率 为 ， 题 意 得 ｚ依
批注本地保存成功开通会员云端永久保存去开通
维普资讯
三种常见统计 图的特点
南京 市第 ２ ９中学 王 菠
在 当今 信息化 时代 ， 据 已经成 为一种 重 要的信 息． 扇形 统 数 而 条 形 统 计 图 、 线 统 计 图 可 以 从 不 同 的 角 度 反 映 一 组 数 据 信 息 的 特 点 与 折 规 律 ， 种 统 计 图 有 着 各 自特 点 ， 此 解 决 实 际 问 题 时 要 注 意 统 计 图 的 三 因 特 点 ， 会 收 集 、 述 、 析 数 据 ， 而 作 出合 理 的 决 策 ． 学 描 分 从
答 下 列 问题．
（）２０ 年 底 的 绿 地 面 积 １ ０４
— —
公 顷 ，比 ２ ０ 年 底 增 加 了 ０３
维普资讯
ቤተ መጻሕፍቲ ባይዱ
基 础 辅 导
公 顷 ；
（ ）在 ２ ０ ２ ０ ２年 、 ０ ３年 、 ０ ４年 ２０ ２０ 这 三 年 中 ， 加 绿 地 面 积 最 多 的 是 增

一、扇形统计图的特点：1．利用圆和扇形来表示总体和部分的关系；2．圆代表总体，各个扇形分别表示总体中不同的部分；3．扇形的大小反映部分占总体的百分比的大小；4．各个扇形的面积之和为一个整圆。

画扇形统计图的步骤： 1. 计算各个部分占总体的百分比；2. 求各个部分的圆心角=360°×各个部分的百分比；3. 画扇形统计图，最后还要在扇形统计图中标注百分比。

二、折线统计图：是用一个单位长度表示一定的数量，根据数量的多少描出各点，然后把各点用线段顺次连接起来，以折线的上升或下降来表示统计数量增减变化。

折线统计图不但可以表示出数量的多少，而且还能够清楚的表示出数量增减变化的情况。

三、条形统计图用一个单位长度(如1厘米)表示一定的数量，根据数量的多少，画成长短相应成比例的直条，并按一定顺序排列起来，这样的统计图，称为条形统计图。

条形统计图可以清楚地表明各种数量的多少。

1、鸡兔同笼，共有头30个，足86只，求鸡兔各有多少只？答：鸡17，兔13。

解，设都是兔，则30只兔应有120条腿，而现在只有86条腿，多算了34条。

这是因为每把一只鸡算成一只兔就会多算两条腿，多算了34条腿一定是因为把17只鸡算成17只兔了，所以鸡是17只，兔就是30-17=13只。

鸡兔同笼问题解题思路都一样。

以下各题就不再解了。

2、有20张5元和10元的人民币，一共是175元，5元和10元的人民币各有多少张？答：15张10元，5张5元。

3、王老师圆珠笔和钢笔共买了15枝，圆珠笔每枝1.5元，钢笔每枝4.5元，共花了49.5元，圆珠笔和钢笔各买了多少枝？答：6支圆珠笔，9支钢笔。

4、鸡兔同笼，鸡兔共35个头，94条腿，问鸡兔各多少只？答：鸡23只，兔12只。

5、在一个停车场内，汽车、摩托车共停了48辆，其中每辆汽车有4个轮子，每辆摩托车有3个轮子，这些车共有172个轮子，停车场内有汽车摩托车各多少辆？答：汽车28辆，摩托车20辆。

扇形统计图有什么特点
扇形统计图的特点：1、圆代表总体 2、扇形代表总体中不同部分 3、扇形大小反映部分占总体的百分比
扇形统计图是用整个圆表示总数（单位“1”），用圆内各个扇形的大小表示各部分量占总量的百分之几，扇形统计图中各部分的百分比之和是单位“1”。

扇形统计图的特点： 1、圆代表总体，各个扇形分别表示总体中不同的部分； 2、扇形的大小反映部分占总体的百分比的大小；3、各个扇形的面积之和为一个整圆。

通过扇形统计图可以很确切地则表示出来各部分数量与总数之间的关系。

与折线统计图相同的就是，无法反应数量变化趋势；与条形统计图相同的就是，无法很难窥见各种数量的多少。

扇形统计图可以更确切的介绍各部分数量同总数之间的关系。

扇形统计图可以使一些杂乱无章的数据显得准确细致，并使人看起来一目了然，有利于排序各种数据，显得更加便利，便捷！。

小学数学六年级上册《统计图的选择》
类别
知 识 要 点
基础性公民素养
陈述性知识
符
号
概
念
命
题
1.读懂条形统计图、折线统计图、扇形统计图，能从中获取有效信息。
2.知道三种统计图的不同特点，能根据需要选择适当的统计图，直观、有效的表示信息。
3.会合理运用三种统计图的特点，解决生活中的问题。
程序性知识
动作Biblioteka 思维提高性公民素养
策略性知识
认
知
方
法
管
理
结合生活实例，抓住语言环境，直观展示统计图让学生感受理解。
创 新性知识
知新组
合
发
散
平
行
合理运用三种统计图的特点与作用。
模
型
规
则
1.结合前一课认识了扇形统计图说出它的特点和运用范围。
2.观察第23届奥运会开始获得金牌，第24——28届奥运会我国获奖牌情况统计表。说一说从统计表中获得信息。
3.观察课件出示的折线统计图、条形统计图、扇形统计图。说统计图的有效信息，感受三种统计图的特点及作用。
4.结合生活实例，抓住语言环境，正确选择统计图。

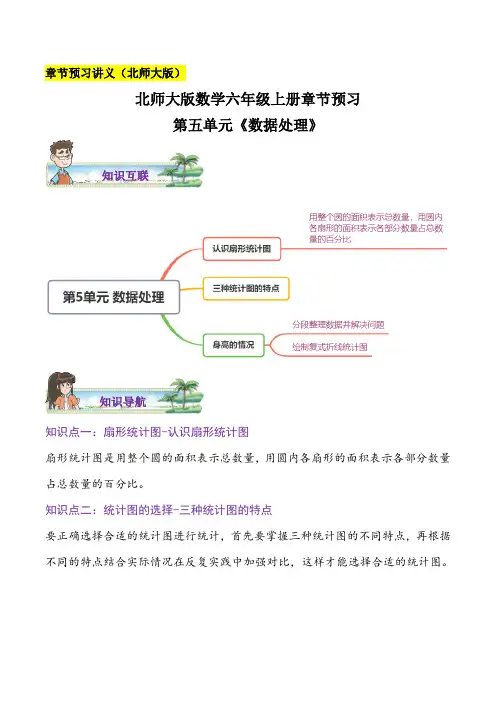
章节预习讲义（北师大版）北师大版数学六年级上册章节预习第五单元《数据处理》知识互联知识导航知识点一：扇形统计图-认识扇形统计图扇形统计图是用整个圆的面积表示总数量，用圆内各扇形的面积表示各部分数量占总数量的百分比。

知识点二：统计图的选择-三种统计图的特点要正确选择合适的统计图进行统计，首先要掌握三种统计图的不同特点，再根据不同的特点结合实际情况在反复实践中加强对比，这样才能选择合适的统计图。

知识点三：身高的情况1.分段整理数据并解决问题在分组整理数据时，要根据实际情况来确定每一段的数量，以便清楚地表达信息。

2.绘制复式折线统计图、选择合适的比较方法分析两组数据的区别在同等情况下，折线越陡，数量变化越大，反之，数量变化越小。

夯实基础一、精挑细选（共5题；每题2分，共10分）1．（2021·广东光明·六年级期末）一辆货车从甲地开往乙地，货车到达乙地后﹐用半小时装卸货物，然后立即返回甲地。

下面的图形中正确描述货车这一过程的是（）。

A．B．C．D．2．（2021·广东徐闻·六年级期末）要想了解部分和总量之间的百分比关系，应选择（）统计图。

A．条形B．折线C．扇形3．（2021·广东廉江·六年级期末）要反映一个村子农作物的种植面积占土地总面积的百分比，应选用（）统计图。

A．扇形B．折线C．条形4．（2020·辽宁西岗·六年级期末）星期日乐乐骑自行车出游，下图描述了乐乐离家的距离随时间变化的情况，下面（）是正确的。

A．乐乐出去6小时后离家最远。

B．乐乐一共骑了3小时的自行车。

C．乐乐在玩了3小时到达离家30千米的地方后立即往回返。

D．乐乐在离家15千米的地方停留了1小时。

5．（2014·全国·期中）如图是甲﹑乙两户居民家庭全年各项支出的统计图．根据统计图，下列对两户家庭教育支出占全年总支出的百分比作出的判断中正确的是（）A．甲户比乙户大B．乙户比甲户大C．甲﹑乙两户一样大D．无法确定哪一户大二、仔细想，认真填（共11题；每空1分，共28分）6．（2021·广东光明·六年级期末）通常状况下，人的身体主要是由水、蛋白质，脂肪、无机物四种成分构成，普通成年人的正常比例是：水占55%，蛋白质占20%，脂肪占20%，无机物占5%。

)
A.1日∼ 10日，甲的步数逐天增加
B.1日∼ 6日，乙的步数逐天减少
C.第9日，甲、乙两人的步数正好相等
D.第11日，甲的步数不一定比乙的步数多
【解析】 1日∼ 5日，乙的步数逐天减少,6日的步数比5日的步数多，故B
项结论错误。
1
2
3
4
5
5.某校七年级共有150名男生，从中随机抽取30名男生在“阳光体育活动”
【解析】 2 + 6 + 9 + 18 + 13 + 2 = 50。
6
7
8
9
（2）请选择一种统计图将整理的结果表示出来。
解：整理的结果如图所示。（答案不唯一）
6
7
8
9
（3）请你根据（2）中绘制的统计图，写出一条从中获得的信息。
成绩为80分的人数最多。（答案不唯一，合理即可）
【回顾与思考】
利用统计图表整理和表示数据有什么好处？
每年的7月正值维苏威火山
（意大利西南部的一座活火山）所在
地的夏天，如图为维苏威火山所在地
的气候资料，根据图中信息推断，关
于维苏威火山所在地气候的说法正确
的是( C )
A.夏季高温多雨，冬季寒冷干燥
B.夏季炎热干燥，冬季温和多雨
C.冬暖夏凉，降水集中在冬季
D.冬冷夏热，降水集中在夏季
6
7
8
9
7.[2022岳阳中考]聚焦“双减”政策落地，凸显寒假作业特色。某学校评选
D.频数直方图
扇形统计图的优缺点
优点：能清楚地表示出各部分在总体中所占的百分比，易于显示每组
数据相对于总数的大小。缺点：不能清楚地表明每一个项目的具体数目。

特点： 用一个单位长度表示一定的数量； 用折线的上升或下降来表示数量的增减 变化情况. 作用： 既可表示各种数量的多少，又可反映出 数量增减变化趋势.
统计图的特点和作用
1、扇形统计图 特点： 用一个圆的面积来表示总数； 用扇形面积的大小来表示占总数的百分比. 作用： 可以清楚地表示各个部分和总体的关系.
2、条形统计图
特点： 用一个单位长度表示一定的数量； 用直线的长短来表示数量的多少. 作用： 用于表示各个数量的多少，对比鲜明.

3、折线统计图

什么叫折线统计图及它有什么特点
折线统计图：是用一个单位长度表示一定的数量，根据数量的多少描出各点，然后把各点用线段顺次连接起来，以折线的上升或下降来表示统计数量增减变化。

折线统计图不但可以表示出数量的多少，而且还能够清楚的表示出数量增减变化的情况。

折线统计图分单式或复式。

复式的折线统计图有图例，用不同颜色或形状的线条区别开来。

特点：易于显示数据变化趋势，可以直观地反映这种变化以及各组之间的差别。

作用：折线统计图可以用来作股市的跌涨。

条形统计图的优点
特点：条形统计图可以清楚地表明各种数量的多少。

统计表是统计图的基础。

要做统
计图，一般会先做统计表。

统计表中的数据很详细，但是不利于直观地分析问题。

如果要
针对某一问题进行研究，就要在统计表的基础上做相应的统计图，其中，条形统计图能够
直观地反映各变量数量的差异，折线图能直观反映各变量的变化趋势。

1、能够使人们一眼看出各个数据的大小。

2、不易比较数据之间的差别。

单式条形统计图和复式条形统计图的相同点是都能让人清楚地看出数量的多少。

不
同点就是单式条形统计图用于比较一个物体，而复式条形统计图用于比较多个物体的数量。

在相同的条件下，展开了n次试验，在这n次试验中，事件a出现的次数na称作事
件a出现的频数。

比值na/n称作事件a出现的频率，并记作fn(a).用文字则表示定义为：每个对象发生的次数与总次数的比值就是频率。

第02讲选择合适的统计图【知识梳理】1、明确每种统计图的特点。

（1）扇形统计图的特点：从图上无法直接看出各部分数量的多少，但可以清楚地看出各部分数量占总数量的百分比。

（2）折线统计图的特点：不仅能看出各个数量的多少，还能够反映数量的增减变化情况，能看出数量变化的幅度。

（3）条形统计图的特点：可以直观地看出各个数量的多少，易于比较数量之间的差别。

【典例精讲】例1接种新冠病毒疫苗可以有效预防新冠病毒感染所致的疾病，截止4月7日24时，我市疫苗累计接种超66万针次。

如果要统计4月7日以来清江浦区每日接种人数的多少情况，应选用( )统计图；如果要反映每日接种疫苗的人数增减变化情况，应选用了( )统计图；如果要反映我市各县区接种人数与接种总人数之间的关系，应选用( )统计图。

【分析】一般来说，如果几个数量是并列的，只要求表示数量的多少时，选条形统计图。

如果表示一个量或几个量增减变化和发展变化趋势，则选折线统计图。

如果要求表示各部分数量与总数量之间的关系，则选扇形统计图；据此解答。

【详解】根据统计图的作用可知：统计4月7日以来清江浦区每日接种人数的多少情况，应选用条形统计图；如果要反映每日接种疫苗的人数增减变化情况，应选用了折线统计图；如果要反映我市各县区接种人数与接种总人数之间的关系，应选用扇形统计图。

【点睛】本题主要考查统计图的选择，牢记三种统计图的作用是解题的关键。

例2下面的统计图和统计表记录了小玲家上月部分费用的支出情况。

请把表格填写完整。

【分析】根据扇形统计图可知：水电、通讯等费用占支出金额的14即25%，再根据统计表可知：伙食费占支出金额的35%，进而可知其他费用占支出金额的1－25%－35%＝40%；用支出金额乘以各自所占分率即可得出各自的费用金额。

【详解】由分析可得：水电、通讯等费用占支出金额的25%；其他费用占支出金额的1－25%－35%＝40%。

水电、通讯等费用：1500×25%＝375（元）伙食费：1500×35%＝525（元）其他费用：1500×（1－25%－35%）＝600（元）故答案为：25%；375；525；40%；600【点睛】本题主要考查扇形统计图与统计表的综合应用，解题时要明确：求一个数的百分之几是多少用乘法。

二、人口年龄结构金字塔
人口年龄结构金字塔图直观地表示了人口的年龄、性
别结构。人口金字塔的每一层代表一个年龄组的人口，上
部代表老年人，下部代表少年儿童；左半部分代表男性，
右半部分代表女性；水平方向的长度表示男性和女性人口
的数202量0/5/8各在总人口中所占的百分比。
6
二.人口金字塔图
人口变化有一 定的惯性，在不同 年龄段又有不同的 死亡率，不同年代 的人口金字塔图呈 现出不同形态。
三.柱状图
我国某地人口迁移和年 龄关系示意图
请说出甲乙两 者之间的内在 联系。
三.柱状图 环渤海经济圈四城市不同年
还适用于表
份人口比重变化图
示某一地理
事物在不同
时间或空间
的动态变化。
下图是环渤海经济圈四城市不同年份人口比重变化图。
下列说法与图不相符的是(D )A．唐山人口比重逐渐减小
B．北京人口吸引力增大
来自中国统计年鉴(1998年)中的 “中国人口转变模式图”
五.曲（折）线图
判读时，主要根据线状统计符号的大体走 向来分析统计对象的量值随时间或空间的连续 变化的规律，要特别注意曲线统计图中的高峰 或低谷以及折线图中的明显的转折点。
五.曲（折）线图
假设只考虑人口 自然增长率，则：
⑥
图中 ③ 人口总量最大；
图中 ① 人口总量最小； 图中 ② 人口总量增加最快； 图中 ④ 人口总量减少最快； 图中 ③⑤ 人口总量基本不变；
C．北京和天津人口比重差距扩大
D．天津和廊坊两市的人口比重持续下降
三.柱状图
按联合国标准，如一地区 ≥60岁人口占总人口比例 达10％或≥65岁的人口达7 ％，则可视为进入老龄化 社会。该省开始进入老龄 化社会的时间在（ ）B A．1990年以前 B．1990-2000年之间 C．2000-2004年之间 D．2004年以后

条形统计图有什么特点
条形统计图的特点是能够使人们一眼看出各个条形统计图，易于比较数据之间的差别，能清楚地表示出数量的多少。

条形统计图可分为单式条形统计图和复式条形统计图，前者只表示1个项目的数据，后者可以同时表示多个项目的数据。

描绘条形图的要素有3个，即组数、组宽度、组限。

绘画条形图时，根据图纸的大小，画出两条互相垂直的线条，作为纵轴和横轴；在横轴上适当分配条形的位置，确定直条的宽度和间隔；在纵轴上确定单位长度，并标出数量的标记和计量单位；再根据数据的大小，画出长短不同的直条，不同数量用不同颜色区分开。