定积分分部积分法
- 格式:pptx
- 大小:1.28 MB
- 文档页数:15
定积分的分部积分法经典例题
定积分的应用一般出现在综合题的最后一题,题型仅有两种:第一,求曲线围成的面积;第二求旋转体体积(绕x轴旋转,绕y轴旋转)。
1.求面积
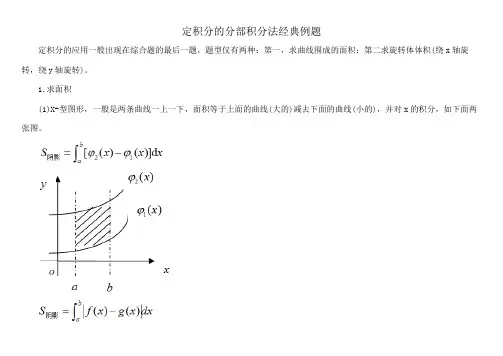
(1)X-型图形,一般是两条曲线一上一下,面积等于上面的曲线(大的)减去下面的曲线(小的),并对x的积分,如下面两张图。
求面积首要问题是画出草图,图形的上下位置(或者左右位置),交点一定要做得准确。
通常曲线,例直线、抛物线、双曲线、指数、对数、三角函数的图像要画得熟练、准确。
求出结果后要检验,这样的题型是一个实际问题,所得结果要合乎逻辑。
(2)Y-型,一般是两条曲线一左一右,面积等于右边的曲线(大的)减去左边的曲线(小的),并对y的积分,如下图
2.旋转体体积
求旋转体体积时要充分发挥几何空间想象能力,要想象出旋转出的体积大概是什么形状的。
(1)X-型图形
绕x轴旋转所得图形的体积
绕y轴旋转所得图形的体积
(2)Y-型图形
绕x轴旋转所得图形的体积
绕y轴旋转所得图形的体积
常考题型如下:。


§6.5 定积分的分部积分法因为vdu udv uv d +=)(,两边从a 到b 取定积分有:⎰⎰⎰+==b abab ab avdu udv uv uv d ][)(,所以 ⎰⎰-=bab a ba vdu uv udv ][ 例1⎰⎰⎰-=-=5151515151]ln [ln ])[(ln ln dx xx x x x xd x x xdx 45ln 5][05ln 551-=--x例2 11|][1110110=+-=-=-==⎰⎰⎰xx xxx x x e e e e dxe xe xde dx xe例3211|c o s 0s i n|s i n s i n c o s 0000-=--=+=-==⎰⎰⎰πππππx dx x x x x xd xdx x例4⎰⎰⎰-==ee e e xd x x x x xd xdx x 1121221ln 21]ln [21)2(ln ln=414|212122122122122+=⋅-=-⎰e x e dx x x e e e例5⎰⎰=2ln 0222ln 032221dx e x dx e x x x 令2x t =,则原式=⎰⎰⎰-==2ln 02ln 02ln 02ln 021][212121dt e te tde dt te tt t t =212ln 212212ln |212)2(ln 212ln 0-=+⋅-=-⋅t e 例6 求⎰⎰=2020c o s c o s ππx xx d e xd xe =dx x e x d e e x x xx⎰⎰+-=-⋅202020sin 1cos |cos πππ=⎰⎰-⋅+-=+-202020sin ])[(sin 1sin 1πππx d e e x xde x xx=xdx e e x cos 1202⎰-+-ππ∴ 1cos 2220-=⎰ππe xdx e x∴ ⎰-=202)1(21cos ππe x e x例7⎰342s i n ππdx xx=⎰⎰+-=-343434cot ]cot [cot ππππππxdx x x x xd=++-=⎰dx x x 34sin cos 493ππππ⎰++-=34sin sin 493ππππx xd 34]sin [ln 493ππππx ++-=23ln 21493++-ππ 利用定积分还可以求某些和的近似值。







求定积分的四种方法在微积分中,确定定积分的值是一个重要的问题。
定积分是一个实函数在给定区间上的积分,表示该函数在该区间上的总体积。
在本文中,我将介绍四种常见的方法来确定定积分的值。
这些方法分别是:几何解释法、Riemann和法、换元积分法和分部积分法。
一、几何解释法例如,如果要计算函数f(x)=x^2在区间[0,1]上的定积分,我们可以将该区间分成无限个小矩形,并计算每个小矩形的面积。
然后将所有小矩形的面积相加,即可得到定积分的值。
对于该例子,我们可以将区间[0,1]分成无限个宽度为dx的小矩形,其高度为f(x)=x^2、因此,定积分的值为∫[0,1]x^2dx=1/3二、Riemann和法Riemann和法是一种将定积分转化为求和的方法。
它使用一个区间分割,把整个区间分成无限个小区间。
然后,通过对每个小区间让其长度趋近于零,计算每个小区间的函数值和相加,从而求得定积分的近似值。
当小区间的数量无限增加时,所得的近似值将趋近于定积分的真正值。
例如,如果要计算函数f(x)=x^2在区间[0,1]上的定积分,我们可以将该区间分成n个小区间,每个区间的宽度为Δx=(1-0)/n,其中n为正整数。
然后,我们可以计算每个小区间的函数值并相加,即可得到定积分的近似值。
当使用Riemann和法时,分割区间的选择对于确定近似值的精确性非常重要。
如果区间分割得足够细,近似值将趋近于定积分的真正值。
三、换元积分法换元积分法是一种通过进行变量替换来简化定积分的方法。
它利用函数的链式法则,将原函数中的自变量替换为新的变量,然后计算新函数的微分。
通过进行适当的变量替换,我们可以将原本复杂的定积分转化为更简单的形式,从而易于计算。
例如,如果要计算函数f(x)=x^2在区间[0,1]上的定积分,我们可以进行变量替换,令u=x^2,则du=2xdx。
通过将原函数中的自变量替换为新变量,我们可以将原本的定积分转化为∫[0,1]u(1/2√u)du。

定积分的换元法与分部积分法定积分是微积分中的重要概念之一,它用于计算曲线与坐标轴之间的面积、弧长等问题。
在定积分的计算过程中,换元法与分部积分法是常用的两种方法。
本文将详细介绍这两种方法的定义、原理和具体应用,并通过实例来加深理解。
一、换元法换元法,也称为反向链式法则,是利用复合函数的导数来进行积分运算。
在定积分的换元法中,我们通过引入一个新的变量来简化被积函数的形式,使得积分的计算更加容易。
具体步骤如下:1. 假设被积函数为f(x),且能够表示为g(u)·u'(x),其中u是一个关于x的函数。
2. 将u关于x求导得到u'(x),并解出x关于u的表达式,即x=g^(-1)(u)。
3. 将f(x)中的x替换为g^(-1)(u),得到f(g^(-1)(u))·u'(x)。
4. 将上述表达式中的dx替换为u'(x)·du。
5. 得到新的被积函数F(u)=f(g^(-1)(u))·u'(x)·du。
6. 对新的被积函数F(u)进行积分。
换元法的主要思想是将原本复杂的积分问题转化为一个简单的积分问题,从而更容易地求解。
下面通过一个例子来说明:例子:计算定积分∫(1+2x)^3·2dx。
解:步骤如下:1. 令1+2x=u,求导得到dx=du/2,将其带入被积函数中得到(1+2x)^3·2·(du/2)。
2. 将x=(u-1)/2,得到被积函数(u^3)·du。
3. 计算新的被积函数的积分即可,∫u^3·du=u^4/4+C,其中C为常数。
4. 将u替换为1+2x,得到最终的结果为(1+2x)^4/4+C。
通过换元法,我们成功地将原本复杂的被积函数简化为了一个简单的表达式,从而更容易地求出其积分。
二、分部积分法分部积分法是用于求解含有积分符号的乘积函数的积分。
在分部积分法中,我们通过对被积函数进行适当的分解和重新组合,使得积分的计算更加容易。