江苏省丹阳市2020学年高中数学第三章空间向量与立体几何3.2.2空间线面关系的判定1学案无答案苏教

§3.2 空间向量的应用3.2.1 直线的方向向量与平面的法向量 3.2.2 空间线面关系的判定(一)——平行关系学习目标 1.掌握空间点、线、面的向量表示.2.理解直线的方向向量与平面的法向量的意义；会用待定系数法求平面的法向量.3.能用向量法证明直线与直线、直线与平面、平面与平面的平行问题．知识点一 直线的方向向量与平面的法向量思考 怎样用向量来表示点、直线、平面在空间中的位置？答案 (1)点：在空间中，我们取一定点O 作为基点，那么空间中任意一点P 的位置就可以用向量OP →来表示．我们把向量OP →称为点P 的位置向量．(2)直线：①直线的方向向量：和这条直线平行或共线的非零向量．②对于直线l 上的任一点P ，在直线上取AB →＝a ，则存在实数t ，使得AP →＝tAB →.(3)平面：①空间中平面α的位置可以由α内两条相交直线来确定．对于平面α上的任一点P ，a ，b 是平面α内两个不共线向量，则存在有序实数对(x ，y )，使得OP →＝x a ＋y b . ②空间中平面α的位置还可以用垂直于平面的直线的方向向量表示． 梳理 (1)用向量表示直线的位置：(2)用向量表示平面的位置：①通过平面α上的一个定点O和两个向量a和b来确定：②通过平面α上的一个定点A和法向量来确定：(3)直线的方向向量和平面的法向量：知识点二利用空间向量处理平行问题思考(1)设v1＝(a1，b1，c1)，v2＝(a2，b2，c2)分别是直线l1，l2的方向向量．若直线l1∥l2，则向量v1，v2应满足什么关系．(2)若已知平面外一直线的方向向量和平面的法向量，则这两向量满足哪些条件可说明直线与平面平行？(3)用向量法处理空间中两平面平行的关键是什么？答案(1)由直线方向向量的定义知若直线l1∥l2，则直线l1，l2的方向向量共线，即l1∥l2⇔v1∥v2⇔v1＝λv2(λ∈R)．(2)可探究直线的方向向量与平面的法向量是否垂直，进而确定线面是否平行．(3)关键是找到两个平面的法向量，利用法向量平行来说明两平面平行．梳理(1)空间中平行关系的向量表示：的法向量分别为μ，v，则设直线l，m的方向向量分别为a，b，平面α，β(2)利用空间向量解决平行问题时，第一，建立立体图形与空间向量的联系，用空间向量表示问题中涉及的点、直线、平面，把立体几何问题转化为向量问题；第二，通过向量的运算，研究平行问题；第三，把向量问题再转化成相应的立体几何问题，从而得出结论．1．若两条直线平行，则它们的方向向量方向相同或相反．(√)2．平面α的法向量是唯一的，即一个平面不可能存在两个不同的法向量．(×) 3．两直线的方向向量平行，则两直线平行．(×)4．直线的方向向量与平面的法向量的方向相同或相反时，直线与平面垂直．(√)类型一 求直线的方向向量、平面的法向量例1 如图，四棱锥P －ABCD 中，底面ABCD 为矩形，P A ⊥平面ABCD ，E 为PD 的中点．AB ＝AP ＝1，AD ＝3，试建立恰当的空间直角坐标系，求平面ACE 的一个法向量．解 因为P A ⊥平面ABCD ，底面ABCD 为矩形， 所以AB ，AD ，AP 两两垂直．如图，以A 为坐标原点，AB →，AD →，AP →的方向为x 轴，y 轴，z 轴的正方向，建立空间直角坐标系A －xyz ，则D (0，3，0)，E ⎝⎛⎭⎫0，32，12，B (1,0,0)，C (1，3，0)，于是AE →＝⎝⎛⎭⎫0，32，12，AC →＝(1，3，0)．设n ＝(x ，y ，z )为平面ACE 的法向量，则⎩⎪⎨⎪⎧n ·AC →＝0，n ·AE →＝0，即⎩⎪⎨⎪⎧x ＋3y ＝0，32y ＋12z ＝0，所以⎩⎨⎧x ＝－3y ，z ＝－3y ，令y ＝－1，则x ＝z ＝ 3.所以平面ACE 的一个法向量为n ＝(3，－1，3)． 引申探究若本例条件不变，试求直线PC 的一个方向向量和平面PCD 的一个法向量． 解 由例1解析图可知，P (0,0,1)，C (1，3，0)， 所以PC →＝(1，3，－1)， 即为直线PC 的一个方向向量． 设平面PCD 的法向量为 n ＝(x ，y ，z )．因为D (0，3，0)，所以PD →＝(0，3，－1)． 由⎩⎪⎨⎪⎧n ·PC →＝0，n ·PD →＝0，即⎩⎨⎧x ＋3y －z ＝0，3y －z ＝0，所以⎩⎨⎧x ＝0，z ＝3y ，令y ＝1，则z ＝ 3.所以平面PCD 的一个法向量为n ＝(0,1，3)． 反思与感悟 利用待定系数法求平面法向量的步骤 (1)设向量：设平面的法向量为n ＝(x ，y ，z )． (2)选向量：在平面内选取两个不共线向量AB →，AC →. (3)列方程组：由⎩⎪⎨⎪⎧n ·AB →＝0，n ·AC →＝0，列出方程组．(4)解方程组：⎩⎪⎨⎪⎧n ·AB →＝0，n ·AC →＝0.(5)赋非零值：取其中一个为非零值(常取±1)．(6)得结论：得到平面的一个法向量．跟踪训练1 如图所示，在四棱锥S －ABCD 中，底面是直角梯形，∠ABC ＝90°，SA ⊥底面ABCD ，且SA ＝AB ＝BC ＝1，AD ＝12，建立适当的空间直角坐标系，求平面SCD 与平面SBA的一个法向量．解 如图，以A 为坐标原点，以AD →，AB →，AS →分别为x ，y ，z 轴的正方向建立空间直角坐标系A －xyz ，则A (0,0,0)，D ⎝⎛⎭⎫12，0，0， C (1,1,0)，S (0,0,1)， 则DC →＝⎝⎛⎭⎫12，1，0， DS →＝⎝⎛⎭⎫－12，0，1. 易知向量AD →＝⎝⎛⎭⎫12，0，0是平面SAB 的一个法向量． 设n ＝(x ，y ，z )为平面SDC 的法向量， 则⎩⎨⎧n ·DC →＝12x ＋y ＝0，n ·DS →＝－12x ＋z ＝0，即⎩⎨⎧y ＝－12x ，z ＝12x .取x ＝2，则y ＝－1，z ＝1，∴平面SDC 的一个法向量为(2，－1,1)． 类型二 证明线线平行问题例2 已知直线l 1与l 2的方向向量分别是a ＝(2,3，－1)，b ＝(－6，－9,3)． 证明：l 1∥l 2.证明 ∵a ＝(2,3，－1)，b ＝(－6，－9,3)，∴a ＝－13b ，∴a ∥b ，即l 1∥l 2.反思与感悟 两直线的方向向量共线时，两直线平行；否则两直线相交或异面．跟踪训练2 已知在四面体ABCD 中，G ，H 分别是△ABC 和△ACD 的重心，则GH 与BD 的位置关系是________． 答案 平行解析 设E ，F 分别为BC 和CD 的中点，则GH →＝GA →＋AH →＝23(EA →＋AF →)＝23EF →，所以GH ∥EF ，所以GH ∥BD .类型三 利用空间向量证明线面、面面平行问题例3 已知正方体ABCD-A 1B 1C 1D 1的棱长为2，E ，F 分别是BB 1，DD 1的中点，求证： (1)FC 1∥平面ADE ； (2)平面ADE ∥平面B 1C 1F .证明 (1)以D 为坐标原点，以DA →，DC →，DD 1—→的方向为x 轴，y 轴，z 轴正方向，建立如图所示的空间直角坐标系D －xyz ，则有D (0,0,0)，A (2，0,0)，C (0,2,0)，C 1(0,2,2)，E (2，2,1)，F (0,0,1)，B 1(2,2,2)，所以FC 1—→＝(0,2,1)，DA →＝(2,0,0)，AE →＝(0,2,1)． 设n 1＝(x 1，y 1，z 1)是平面ADE 的法向量， 则n 1⊥DA →，n 1⊥AE →，即⎩⎪⎨⎪⎧n 1·DA →＝2x 1＝0，n 1·AE →＝2y 1＋z 1＝0，得⎩⎪⎨⎪⎧x 1＝0，z 1＝－2y 1，令z 1＝2，则y 1＝－1，所以n 1＝(0，－1,2)． 因为FC 1—→·n 1＝－2＋2＝0，所以FC 1—→⊥n 1. 又因为FC 1⊄平面ADE ，所以FC 1∥平面ADE .(2)因为C 1B 1—→＝(2,0,0)，设n 2＝(x 2，y 2，z 2)是平面B 1C 1F 的一个法向量．由n 2⊥FC 1—→，n 2⊥C 1B 1—→，得⎩⎪⎨⎪⎧n 2·FC 1—→＝2y 2＋z 2＝0，n 2·C 1B 1—→＝2x 2＝0，得⎩⎪⎨⎪⎧x 2＝0，z 2＝－2y 2.令z 2＝2，得y 2＝－1，所以n 2＝(0，－1,2)， 因为n 1＝n 2，所以平面ADE ∥平面B 1C 1F .反思与感悟 利用向量证明平行问题，可以先建立空间直角坐标系，求出直线的方向向量和平面的法向量，然后根据向量之间的关系证明平行问题．跟踪训练3 如图，在四棱锥P －ABCD 中，P A ⊥平面ABCD ，PB 与底面所成的角为45°，底面ABCD 为直角梯形，∠ABC ＝∠BAD ＝90°，P A ＝BC ＝12AD ＝1，问在棱PD 上是否存在一点E ，使CE ∥平面P AB ？若存在，求出E 点的位置；若不存在，请说明理由．解 以A 为坐标原点．分别以AB ，AD ，AP 所在直线为x 轴，y 轴，z 轴建立空间直角坐标系A －xyz ，如图所示．∴P (0,0,1)，C (1,1,0)，D (0,2,0)， 设存在满足题意的点E (0，y ，z )， 则PE →＝(0，y ，z －1)， PD →＝(0,2，－1)， ∵PE →∥PD →，∴y ×(－1)－2(z －1)＝0，①∵AD →＝(0,2,0)是平面P AB 的法向量， 又CE →＝(－1，y －1，z )，CE ∥平面P AB ， ∴CE →⊥AD →，∴(－1，y －1，z )·(0,2,0)＝0.∴y ＝1，代入①得z ＝12，∴E 是PD 的中点，∴存在点E ，当点E 为PD 中点时，CE ∥平面P AB .1．若点A (－1,0,1)，B (1,4,7)在直线l 上，则直线l 的一个方向向量的坐标可以是________．(填序号)①(－1,0,1)；②(1,4,7)；③(2,4,6)． 答案 ③解析 显然AB →＝(2,4,6)可以作为直线l 的一个方向向量．2．已知a ＝(2,4,5)，b ＝(3，x ，y )分别是直线l 1，l 2的方向向量．若l 1∥l 2，则x ＝________，y ＝________. 答案 6152解析 由l 1∥l 2得，23＝4x ＝5y ，解得x ＝6，y ＝152.3．已知向量n ＝(2，－3,1)是平面α的一个法向量，则下列向量中能作为平面α的法向量的是________．(填序号)①n 1＝(0，－3,1)；②n 2＝(－2,0,4)； ③n 3＝(－2，－3,1)；④n 4＝(－2,3，－1)． 答案 ④解析 由题可知只有④可以作为α的法向量．4．已知向量n ＝(－1,3,1)为平面α的法向量，点M (0,1,1)为平面内一定点．P (x ，y ，z )为平面内任一点，则x ，y ，z 满足的关系式是________． 答案 x －3y －z ＋4＝0解析 由题可知MP →＝(x ，y －1，z －1)． 又因为n ·MP →＝0，故－x ＋3(y －1)＋(z －1)＝0，化简， 得x －3y －z ＋4＝0.5．若直线l ∥α，且l 的方向向量为(2，m,1)，平面α的法向量为⎝⎛⎭⎫1，12，2，则m 为________． 答案 －8解析 ∵l ∥α，平面α的法向量为⎝⎛⎭⎫1，12，2， ∴(2，m,1)·⎝⎛⎭⎫1，12，2＝0， ∴2＋12m ＋2＝0，∴m ＝－8.1．应用向量法证明线面平行问题的方法： (1)证明直线的方向向量与平面的法向量垂直．(2)证明直线的方向向量与平面内的某一直线的方向向量共线．(3)证明直线的方向向量可用平面内的任意两个不共线的向量表示．即用平面向量基本定理证明线面平行．2．证明面面平行的方法：设平面α的法向量为n 1＝(a 1，b 1，c 1)，平面β的法向量为n 2＝(a 2，b 2，c 2)，则α∥β⇔n 1∥n 2⇔(a 1，b 1，c 1)＝k (a 2，b 2，c 2)(k ∈R )．一、填空题1．已知l 1的方向向量为v 1＝(1,2,3)，l 2的方向向量为v 2＝(λ，4,6)，若l 1∥l 2，则λ＝________. 答案 2解析 ∵l 1∥l 2，∴v 1∥v 2，则1λ＝24，∴λ＝2.2．已知a ＝(λ＋1,0,2)，b ＝(6,2μ－1,2λ)，若a ∥b ，则μ的值为________． 答案 12解析 因为a ∥b ，故2μ－1＝0，即μ＝12.3．直线l 的方向向量s ＝(－1,1,1)，平面α的一个法向量为n ＝(2，x 2＋x ，－x )，若直线l ∥α，则x 的值为________． 答案 ±2解析 易知－1×2＋1×(x 2＋x )＋1×(－x )＝0， 解得x ＝±2.4．设平面α的法向量为(1,2，－2)，平面β的法向量为(－2，－4，k )，若α∥β，则k 的值为________． 答案 4解析 因为α∥β，所以平面α与平面β的法向量共线， 所以(－2，－4，k )＝λ(1,2，－2)， 所以⎩⎪⎨⎪⎧－2＝λ，－4＝2λ，k ＝－2λ，解得⎩⎪⎨⎪⎧λ＝－2，k ＝4.所以k 的值是4.5．已知平面α内两向量a ＝(1,1,1)，b ＝(0,2，－1)且c ＝m a ＋n b ＋(4，－4,1)．若c 为平面α的法向量，则m ，n 的值分别为________． 答案 －1,2解析 c ＝m a ＋n b ＋(4，－4,1)＝(m ，m ，m )＋(0,2n ，－n )＋(4，－4,1)＝(m ＋4，m ＋2n －4，m －n ＋1)，由c 为平面α的法向量，得⎩⎪⎨⎪⎧ c ·a ＝0，c ·b ＝0，得⎩⎪⎨⎪⎧m ＝－1，n ＝2.6．已知A (4,1,3)，B (2,3,1)，C (3,7，－5)，点P (x ，－1,3)在平面ABC 内，则x 的值为________． 答案 11解析 ∵点P 在平面ABC 内， ∴存在实数k 1，k 2， 使AP →＝k 1AB →＋k 2AC →，即(x －4，－2,0)＝k 1(－2,2，－2)＋k 2(－1,6，－8)，∴⎩⎪⎨⎪⎧ 2k 1＋6k 2＝－2，k 1＋4k 2＝0，解得⎩⎪⎨⎪⎧k 1＝－4，k 2＝1.∴x －4＝－2k 1－k 2＝8－1＝7， 即x ＝11.7．已知l ∥α，且l 的方向向量为m ＝(2，－8,1)，平面α的法向量为n ＝(1，y,2)，则y ＝________.答案 12解析 ∵l ∥α，∴l 的方向向量m ＝(2，－8,1)与平面α的法向量n ＝(1，y,2)垂直，∴2×1－8×y ＋2＝0，∴y ＝12. 8．若平面α的一个法向量为u 1＝(－3，y,2)，平面β的一个法向量为u 2＝(6，－2，z )，且α∥β，则y ＋z ＝________.答案 －3解析 ∵α∥β，∴u 1∥u 2，∴－36＝y －2＝2z. ∴y ＝1，z ＝－4.∴y ＋z ＝－3.9．已知平面α与平面β平行，若平面α与平面β的法向量分别为μ＝(5,25,5)，v ＝(t,5,1)，则t 的值为________．答案 1解析 ∵平面α与平面β平行，∴平面α的法向量μ与平面β的法向量v 平行，∴5t ＝255＝51，解得t ＝1. 10．已知平面α内的三点A (0,0,1)，B (0,1,0)，C (1,0,0)，平面β的一个法向量为n ＝(－1，－1，－1)，且β与α不重合，则β与α的位置关系是________．答案 α∥β解析 AB →＝(0,1，－1)，AC →＝(1,0，－1)，n ·AB →＝(－1，－1，－1)·(0,1，－1)＝－1×0＋(－1)×1＋(－1)×(－1)＝0，n ·AC →＝(－1，－1，－1)·(1,0，－1)＝－1×1＋0＋(－1)·(－1)＝0，∴n ⊥AB →，n ⊥AC →.∴n 也为α的一个法向量．又α与β不重合，∴α∥β.11．若平面α的一个法向量为u 1＝(m,2，－4)，平面β的一个法向量为u 2＝(6，－4，n )，且α∥β，则m ＋n ＝________.答案 5解析 ∵α∥β，∴u 1∥u 2.∴m 6＝2－4＝－4n∴m ＝－3，n ＝8.∴m ＋n ＝5.二、解答题12．如图，在正方体ABCD －A 1B 1C 1D 1中，求证：AC 1—→是平面B 1D 1C 的法向量．证明 如图，以D 为坐标原点，DA ，DC ，DD 1分别为x ，y ，z 轴，建立空间直角坐标系．设正方体的棱长为1，则D 1(0,0,1)，A (1,0,0)，C (0,1,0)，B 1(1,1,1)，C 1(0,1,1)．所以AC 1—→＝(－1,1,1)，D 1B 1—→＝(1,1,0)，CB 1—→＝(1,0,1)，所以AC 1—→·D 1B 1—→＝(－1,1,1)·(1,1,0)＝0，AC 1—→·CB 1—→＝(－1,1,1)·(1,0,1)＝0，所以AC 1—→⊥D 1B 1—→，AC 1—→⊥CB 1→，又B 1D 1∩CB 1＝B 1，且B 1D 1，CB 1⊂平面B 1D 1C ，所以AC 1⊥平面B 1D 1C ，AC 1—→是平面B 1D 1C 的法向量．13．已知A ⎝⎛⎭⎫0，2，198，B ⎝⎛⎭⎫1，－1，58，C ⎝⎛⎭⎫－2，1，58是平面α内的三点，设平面α的法向量a ＝(x ，y ，z )，求x ∶y ∶z 的值．解 AB →＝⎝⎛⎭⎫1，－3，－74，AC →＝⎝⎛⎭⎫－2，－1，－74， 由⎩⎪⎨⎪⎧ a ·AB →＝0，a ·AC →＝0，得⎩⎨⎧ x －3y －74z ＝0，－2x －y －74z ＝0， 解得⎩⎨⎧x ＝23y ，z ＝－43y ， 则x ∶y ∶z ＝23y ∶y ∶⎝⎛⎭⎫－43y ＝2∶3∶(－4)． 三、探究与拓展14.已知O ，A ，B ，C ，D ，E ，F ，G ，H 为空间的9个点(如图所示)，并且OE →＝kOA →，OF →＝kOB →，OH →＝kOD →，AC →＝AD →＋mAB →，EG →＝EH →＋mEF →.求证：(1)A ，B ，C ，D 四点共面，E ，F ，G ，H 四点共面；(2)AC →∥EG →.证明 (1)由AC →＝AD →＋mAB →，EG →＝EH →＋mEF →，知A ，B ，C ，D 四点共面，E ，F ，G ，H 四点共面．(2)∵EG →＝EH →＋mEF →＝OH →－OE →＋m (OF →－OE →)＝k (OD →－OA →)＋km (OB →－OA →)＝kAD →＋kmAB →＝k (AD →＋mAB →)＝kAC →，∴AC →∥EG →.15.如图所示，在正方体ABCD －A 1B 1C 1D 1中，O 为底面ABCD 的中心，P 是DD 1的中点，设Q 是CC 1上的点，问：当点Q 在什么位置时，平面D 1BQ ∥平面P AO?解 如图所示，以点D 为坐标原点，分别以DA ，DC ，DD 1所在直线为x ，y ，z 轴，建立空间直角坐标系，在CC 1上任取一点Q ，连结BQ ，D 1Q .设正方体的棱长为1，则O ⎝⎛⎭⎫12，12，0，P ⎝⎛⎭⎫0，0，12， A (1,0,0)，B (1,1,0)，D 1(0,0,1)，则Q (0,1，z )，则OP →＝⎝⎛⎭⎫－12，－12，12， BD 1→＝(－1，－1,1)，∴OP →∥BD 1—→，∴OP ∥BD 1.AP →＝⎝⎛⎭⎫－1，0，12，BQ →＝(－1,0，z )， 当z ＝12时，AP →＝BQ →， 即当AP ∥BQ 时，有平面P AO ∥平面D 1BQ ， ∴当Q 为CC 1的中点时，平面D 1BQ ∥平面P AO .。

空间向量的数量积（2）学习目的：1.掌握空间向量的模长公式、夹角公式、两点间的距离公式，会用这些公式解决有关问题；2.会根据向量的坐标判断两个向量共线或垂直学习重点：夹角公式、距离公式学习难点：模长公式、夹角公式、两点间的距离公式及其运用学习过程： 一、复习1.空间直角坐标系：2.空间直角坐标系中的坐标3.空间向量的直角坐标运算律 二、讲解新课： 1.模长公式若123(,,)a a a a =r ，123(,,)b b b b =r， 有332211b a b a b a ++=⋅,则||a ==r||b ==r2.夹角公式cos ||||a b a b a b ⋅⋅==⋅r rr rrr ．3.两点间的距离公式：若111(,,)A x y z ，222(,,)B x y z ，则||AB ==u u r ，或,A B d = 三、讲解范例例1已知(3,3,1)A ，(1,0,5)B ， 求：（1）线段AB 的中点坐标和长度；（2）到,A B 两点的距离相等的点(,,)P x y z 的坐标,,x y z 满足的条件点评：到,A B 两点的距离相等的点(,,)P x y z 构成的集合就是线段AB 的中垂面，若将点P 的坐标,,x y z 满足的条件46870x y z +-+=的系数构成一个向量(4,68)a =-r，与(2,3,4)AB =--u u r 共线. 例2 正方体1111ABCD A B C D -中，点11,F E 分别在棱1111,D A B A 上，且,41111111B A F D E B == 求1BE 与1DF 所成角的余弦.例3 已知三角形的顶点是(1,1,1)A -，(2,1,1)B -，(1,1,2)C ---，试求这个三角形的面积.点评：三角形的内角可看成由该角的顶点出发的两边所在向量的夹角.例4如图,在棱长为1的正方体1111D C B A ABCD -中,F E ,分别是BD D D ,1的中点,G 在棱CD 上,且CD CG 41=,H 为G C 1中点,应用空间向量的运算办法解决下列问题: (1)求证:C B EF 1⊥; (2)求EF 与G C 1所成的角的余弦; (3)求FH 的长.四、练习 ：教材95页练习 五、小结 ：1．空间向量的模长公式、两点间的距离公式的形式与平面向量中相关内容一致，因此可类比记忆； 2．在计算异面直线所成角时，仍然用向量数量积的知识，建立空间直角坐标系后能方便的求出向量的坐标，则通常考虑用坐标运算来求角3．对于一些较特殊的几何体或平面图形中有关夹角，距离，垂直，平行的问题，都可以通过建立坐标系将其转化为向量间的夹角，模，垂直，平行的问题，从而利用向量的坐标运算求解，并可以使解法简单化．值得注意的是——坐标系的选取要合理、适当． 六、作业1：1、求下列各题中两个向量夹角的大小（1）)0,0,1(),3,3,2(=-= （2）)2,1,1(),2,4,2(=-=ABC D E FG HA 1B 1C 1D 12若(3cos ,3sin ,1)A θθ，)1,sin 5,(cos θθB ，求||AB uuu r的取值范围；3．若(cos ,sin ,2sin )P ααα，(2cos ,2sin ,1)Q ββ，求||PQ u u r的最大值和最小值4、在空间四边形ABCD 中，已知G 为BCD ∆的重心，H F E ,,分别为边AD CD ,和BC 的中点，化简下列各式： （1）;2131CA BE AG ++（2）);(21AD AC AB -+（3）;313131AD AC AB ++5．在长方体1111D C B A ABCD -中，c AA b BC a AB ===1,,，求异面直线1BD 和C B 1所成角的余弦值。

3.2.2 利用向量解决平行、垂直问题1．用向量方法证明空间中的平行关系(1)证明线线平行设直线l，m的方向向量分别是a＝(a1，b1，c1)，b＝(a2，b2，c2)，则l∥m⇔□01a∥b⇔□02 a＝λb⇔□03a1＝λa2，b1＝λb2，c1＝λc2(λ∈R)．(2)证明线面平行设直线l的方向向量为a＝(a1，b1，c1)，平面α的法向量为u＝(a2，b2，c2)，则l∥α⇔□04a⊥u⇔□05a·u＝0⇔□06a1a2＋b1b2＋c1c2＝0.(3)证明面面平行①设平面α，β的法向量分别为u＝(a1，b1，c1)，v＝(a2，b2，c2)，则α∥β⇔□07u∥v⇔u＝λv⇔□08a1＝λa2，b1＝λb2，c1＝λc2(λ∈R)．②由面面平行的判定定理，要证明面面平行，只要转化为相应的线面平行、线线平行即可．2．用向量方法证明空间中的垂直关系(1)证明线线垂直设直线l1的方向向量u1＝(a1，b1，c1)，直线l2的方向向量u2＝(a2，b2，c2)，则l1⊥l2⇔□09u1⊥u2⇔□10u1·u2＝0⇔□11a1a2＋b1b2＋c1c2＝0.(2)证明线面垂直设直线l的方向向量是u＝(a1，b1，c1)，平面α的法向量v＝(a2，b2，c2)，则l⊥α⇔□12 u∥v⇔□13u＝λv(λ∈R)⇔□14a1＝λa2，b1＝λb2，c1＝λc2(λ∈R)．(3)证明面面垂直若平面α的法向量u＝(a1，b1，c1)，平面β的法向量v＝(a2，b2，c2)，则α⊥β⇔□15u ⊥v⇔□16u·v＝0⇔□17a1a2＋b1b2＋c1c2＝0.1．判一判(正确的打“√”，错误的打“×”)(1)若两直线方向向量的数量积为0，则这两条直线一定垂直相交．( )(2)若一直线与平面垂直，则该直线的方向向量与平面内的所有直线的方向向量的数量积为0.( )(3)两个平面垂直，则其中一平面内的直线的方向向量与另一平面内的直线的方向向量垂直．( )答案 (1)× (2)√ (3)×2．做一做(请把正确的答案写在横线上)(1)若直线l 1的方向向量为u 1＝(1,3,2)，直线l 2上有两点A (1,0,1)，B (2，－1,2)，则两直线的位置关系是________．(2)若直线l 的方向向量为a ＝(1,0,2)，平面α的法向量为n ＝(－2,0，－4)，则直线l 与平面α的位置关系为________．(3)已知两平面α，β的法向量分别为u 1＝(1,0,1)，u 2＝(0,2,0)，则平面α，β的位置关系为________．(4)若平面α，β的法向量分别为(－1,2,4)，(x ，－1，－2)，并且α⊥β，则x 的值为________．答案 (1)垂直 (2)垂直 (3)垂直 (4)－10探究1 利用空间向量解决平行问题例1 已知正方体ABCD －A 1B 1C 1D 1的棱长为2，E ，F 分别是BB 1，DD 1的中点，求证： (1)FC 1∥平面ADE ； (2)平面ADE ∥平面B 1C 1F .[证明] (1)如图所示，建立空间直角坐标系Dxyz ，则有D (0,0,0)，A (2,0,0)，C 1(0,2,2)，E (2,2,1)，F (0，0,1)，B 1(2,2,2)， 所以FC 1→＝(0,2,1)，DA →＝(2,0,0)，AE →＝(0,2,1)．设n 1＝(x 1，y 1，z 1)是平面ADE 的法向量，则n 1⊥DA →，n 1⊥AE →， 即⎩⎪⎨⎪⎧n 1·DA →＝2x 1＝0，n 1·AE →＝2y 1＋z 1＝0，得⎩⎪⎨⎪⎧x 1＝0，z 1＝－2y 1，令z 1＝2，则y 1＝－1，所以n 1＝(0，－1,2)． 因为FC 1→·n 1＝－2＋2＝0，所以FC 1→⊥n 1.又因为FC 1⊄平面ADE ，所以FC 1∥平面ADE . (2)因为C 1B 1→＝(2,0,0)，设n 2＝(x 2，y 2，z 2)是平面B 1C 1F 的一个法向量． 由n 2⊥FC 1→，n 2⊥C 1B 1→，得 ⎩⎪⎨⎪⎧n 2·FC 1→＝2y 2＋z 2＝0，n 2·C 1B 1→＝2x 2＝0，得⎩⎪⎨⎪⎧x 2＝0，z 2＝－2y 2.令z 2＝2，得y 2＝－1，所以n 2＝(0，－1,2)， 因为n 1＝n 2，所以平面ADE ∥平面B 1C 1F . 拓展提升利用向量法证明平行问题的两种途径(1)利用三角形法则和平面向量基本定理实现向量间的相互转化，得到向量的共线关系； (2)通过建立空间直角坐标系，借助直线的方向向量和平面的法向量进行平行关系的证明．【跟踪训练1】 在长方体ABCD －A 1B 1C 1D 1中，AB ＝4，AD ＝3，AA 1＝2，P ，Q ，R ，S 分别是AA 1，D 1C 1，AB ，CC 1的中点．求证：PQ ∥RS .证明 证法一：以D 为原点，DA ，DC ，DD 1所在直线分别为x 轴、y 轴、z 轴，建立如图所示的空间直角坐标系Dxyz .则P (3,0,1)，Q (0,2,2)，R (3,2,0)，S (0,4,1)， PQ →＝(－3,2,1)，RS →＝(－3,2,1)，∴PQ →＝RS →，∴PQ →∥RS →，即PQ ∥RS . 证法二：RS →＝RC →＋CS →＝12DC →－DA →＋12DD 1→，PQ →＝PA 1→＋A 1Q →＝12DD 1→＋12DC →－DA →，∴RS →＝PQ →，∴RS →∥PQ →，即RS ∥PQ . 探究2 利用空间向量解决垂直问题例2 如图，在四棱锥E －ABCD 中，AB ⊥平面BCE ，CD ⊥平面BCE ，AB ＝BC ＝CE ＝2CD ＝2，∠BCE ＝120°.求证：平面ADE ⊥平面ABE .[证明] 取BE 的中点O ，连接OC ，则OC ⊥EB ， 又AB ⊥平面BCE .∴以O 为原点建立空间直角坐标系Oxyz .如图所示．则由已知条件有C (1，0,0)，B (0，3，0)，E (0，－3，0)，D (1,0,1)，A (0，3，2)． 设平面ADE 的法向量为n ＝(a ，b ，c )，则n ·EA →＝(a ，b ，c )·(0,23，2)＝23b ＋2c ＝0，n ·DA →＝(a ，b ，c )·(－1，3，1)＝－a ＋3b ＋c ＝0.令b ＝1，则a ＝0，c ＝－3， ∴n ＝(0,1，－3)．∵AB ⊥平面BCE ，∴AB ⊥OC ，又OC ⊥EB ，且EB ∩AB ＝B ，∴OC ⊥平面ABE ， ∴平面ABE 的法向量可取为m ＝(1,0,0)． ∵n ·m ＝(0,1，－3)·(1,0,0)＝0， ∴n ⊥m ，∴平面ADE ⊥平面ABE . 拓展提升利用向量法证明几何中的垂直问题的两条途径(1)利用三角形法则和平面向量基本定理实现向量间的相互转化，得到向量的垂直关系． (2)通过建立空间直角坐标系，借助直线的方向向量和平面的法向量进行证明．证明线面垂直时，只需直线的方向向量与平面的法向量平行或直线的方向向量与平面内两相交的直线的方向向量垂直．在判定两个平面垂直时，只需求出这两个平面的法向量，再看它们的数量积是否为0.【跟踪训练2】 如右图所示，在正方体ABCD －A 1B 1C 1D 1中，E ，F 分别是BB 1，D 1B 1的中点．求证：EF ⊥平面B 1AC .证明 证法一：设AB →＝a ，AD →＝c ，AA 1→＝b ，则EF →＝EB 1→＋B 1F →＝12(BB 1→＋B 1D 1→)＝12(AA 1→＋BD →)＝12(AA 1→＋AD →－AB →)＝12(－a ＋b ＋c )，∵AB 1→＝AB →＋AA 1→＝a ＋b .∴EF →·AB 1→＝12(－a ＋b ＋c )·(a ＋b )＝12(b 2－a 2＋c ·a ＋c ·b ) ＝12(|b |2－|a |2＋0＋0)＝0. ∴EF →⊥AB 1→，即EF ⊥AB 1，同理，EF ⊥B 1C . 又AB 1∩B 1C ＝B 1， ∴EF ⊥平面B 1AC .证法二：设正方体的棱长为2，以DA ，DC ，DD 1所在直线分别为x 轴、y 轴、z 轴建立如图所示的直角坐标系，则A (2,0,0)，C (0,2,0)，B 1(2,2,2)，E (2,2,1)，F (1,1,2)．∴EF →＝(1,1,2)－(2,2,1) ＝(－1，－1,1)．AB 1→＝(2,2,2)－(2,0,0)＝(0,2,2)，AC →＝(0,2,0)－(2,0,0)＝(－2,2,0)，∴EF →·AB 1→＝(－1，－1,1)·(0,2,2)＝(－1)×0＋(－1)×2＋1×2＝0.EF →·AC →＝(－1，－1,1)·(－2,2,0)＝2－2＋0＝0， ∴EF →⊥AB 1→，EF →⊥AC →， ∴EF ⊥AB 1，EF ⊥AC . 又AB 1∩AC ＝A ， ∴EF ⊥平面B 1AC .证法三：同法二得AB 1→＝(0,2,2)，AC →＝(－2,2,0)， EF →＝(－1，－1,1)．设面B 1AC 的法向量n ＝(x ，y ，z )， 则AB →1·n ＝0，AC →·n ＝0，即⎩⎪⎨⎪⎧2y ＋2z ＝0，－2x ＋2y ＝0，取x ＝1，则y ＝1，z ＝－1，∴n ＝(1,1，－1)，∴EF →＝－n ，∴EF →∥n ，∴EF ⊥平面B 1AC . 探究3 与平行、垂直有关的探索性问题例3 如图，在三棱锥P －ABC 中，AB ＝AC ，D 为BC 的中点，PO ⊥平面ABC ，垂足O 落在线段AD 上，已知BC ＝8，PO ＝4，AO ＝3，OD ＝2.(1)证明：AP ⊥BC ；(2)在线段AP 上是否存在点M ，使得平面AMC ⊥平面BMC ？若存在，求出AM 的长；若不存在，请说明理由．[解] (1)证明：如图，以O 为原点，以射线OD 为y 轴的正半轴，射线OP 为z 轴的正半轴，建立空间直角坐标系Oxyz .则O (0,0,0)，A (0，－3,0)，B (4,2,0)，C (－4,2,0)，P (0,0,4)， AP →＝(0,3,4)，BC →＝(－8,0,0)，由此可得AP →·BC →＝0，所以AP →⊥BC →，即AP ⊥BC .(2)假设存在满足题意的M ，设PM →＝λPA →，λ≠1，则PM →＝λ(0，－3，－4)．BM →＝BP →＋PM →＝BP →＋λPA →＝(－4，－2,4)＋λ(0，－3，－4)＝(－4，－2－3λ，4－4λ)，AC →＝(－4,5,0)．设平面BMC 的法向量n 1＝(x 1，y 1，z 1)， 平面APC 的法向量n 2＝(x 2，y 2，z 2)． 由⎩⎪⎨⎪⎧BM →·n 1＝0，BC →·n 1＝0，得⎩⎪⎨⎪⎧－4x 1－(2＋3λ)y 1＋(4－4λ)z 1＝0，－8x 1＝0，即⎩⎪⎨⎪⎧x 1＝0，z 1＝2＋3λ4－4λy 1，可取n 1＝⎝ ⎛⎭⎪⎫0，1，2＋3λ4－4λ.由⎩⎪⎨⎪⎧AP →·n 2＝0，AC →·n 2＝0，即⎩⎪⎨⎪⎧3y 2＋4z 2＝0，－4x 2＋5y 2＝0，得⎩⎪⎨⎪⎧x 2＝54y 2，z 2＝－34y 2，可取n 2＝(5,4，－3)，由n 1·n 2＝0，得4－3×2＋3λ4－4λ＝0，解得λ＝25，故PM →＝⎝ ⎛⎭⎪⎫0，－65，－85，AM →＝AP →＋PM →＝⎝ ⎛⎭⎪⎫0，95，125，所以AM ＝3.综上所述，存在点M 符合题意，AM ＝3. 拓展提升利用向量解决探索性问题的方法对于探索性问题，一般先假设存在，利用空间坐标系，结合已知条件，转化为代数方程是否有解的问题，若有解满足题意则存在，若没有满足题意的解则不存在．【跟踪训练3】 如图，直三棱柱ABC －A 1B 1C 1中，AC ＝3，BC ＝4，AB ＝5，AA 1＝4.(1)求证：BC 1⊥平面AB 1C ；(2)在AB 上是否存在点D ，使得AC 1∥平面CDB 1.解 (1)证明：由已知AC ＝3，BC ＝4，AB ＝5，因而△ABC 是∠ACB 为直角的直角三角形，由三棱柱是直三棱柱，则CC 1⊥平面ABC ，以CA ，CB ，CC 1分别为x ，y ，z 轴建立空间直角坐标系，从而CA →＝(3,0,0)，BC 1→＝(0，－4,4)，则BC 1→·CA →＝(0，－4,4)·(3,0,0)＝0，则BC 1→⊥AC →，所以BC 1⊥AC .又四边形BCC 1B 1为正方形，因而BC 1⊥B 1C .又∵B 1C ∩AC ＝C ，∴BC 1⊥平面AB 1C .(2)假设存在点D (x ，y,0)，使得AC 1∥平面CDB 1，CD →＝(x ，y,0)，CB 1→＝(0,4,4)， 设平面CDB 1的法向量m ＝(a ，b ，c )，则⎩⎪⎨⎪⎧m ·CD →＝0，m ·CB 1→＝0，即⎩⎪⎨⎪⎧xa ＋yb ＝0，4b ＋4c ＝0.令b ＝－x ，则c ＝x ，a ＝y ，所以m ＝(y ，－x ，x )，而AC 1→＝(－3,0,4)，则AC 1→·m ＝0，得－3y ＋4x ＝0.① 由D 在AB 上，A (3,0,0)，B (0,4,0)得x －3－3＝y4，即得4x ＋3y ＝12，② 联立①②可得x ＝32，y ＝2，∴D ⎝ ⎛⎭⎪⎫32，2，0，即D 为AB 的中点． 综上，在AB 上存在点D ，使得AC 1∥平面CDB 1，点D 为AB 的中点．1.利用向量证明线线平行的两种思路一是建立空间直角坐标系，通过坐标运算，利用向量平行的坐标表示证明；二是用基底思路，通过向量的线性运算，利用共线向量定理证明.2.向量法证明线线垂直的方法用向量法证明空间中两条直线相互垂直，其主要思路是证明两条直线的方向向量相互垂直．具体方法为：(1)坐标法：根据图形的特征，建立适当的空间直角坐标系，准确地写出相关点的坐标，表示出两条直线的方向向量，证明其数量积为0.(2)基向量法：利用向量的加减运算，结合图形，将要证明的两条直线的方向向量用基向量表示出来．利用数量积运算说明两向量的数量积为0.3.向量法证明线面垂直的方法(1)向量基底法，具体步骤如下：①设出基向量，用基向量表示直线的方向向量；②找出平面内两条相交直线的方向向量并分别用基向量表示；③分别计算直线的方向向量与平面内两条相交直线的方向向量的数量积.(2)坐标法，具体方法如下：方法一：①建立空间直角坐标系；②将直线的方向向量用坐标表示；③将平面内任意两条相交直线的方向向量用坐标表示；④分别计算直线的方向向量与平面内两条相交直线的方向向量的数量积.方法二：①建立空间直角坐标系；②将直线的方向向量用坐标表示；③求平面的法向量；④说明平面的法向量与直线的方向向量平行.4.证明面面垂直的两种思路一是证明其中一个平面过另一个平面的垂线，即转化为线面垂直；二是证明两平面的法向量垂直.1．已知线段AB的两端点坐标为A(9，－3,4)，B(9,2,1)，则线段AB与坐标平面( ) A．xOy平行B．xOz平行C．yOz平行D．yOz相交答案 C解析 因为AB →＝(9,2,1)－(9，－3,4)＝(0,5，－3)，所以AB ∥平面yOz .2．若两个不同平面α，β的法向量分别为u ＝(1,2，－1)，v ＝(－3，－6,3)，则( ) A ．α∥β B ．α⊥βC ．α，β相交但不垂直D ．以上均不正确 答案 A解析 ∵v ＝－3u ，∴α∥β.3．已知直线l 与平面α垂直，直线l 的一个方向向量为u ＝(1，－3，z )，向量v ＝(3，－2,1)与平面α平行，则z 等于( )A ．3B ．6C ．－9D ．9 答案 C解析 ∵l ⊥α，v 与平面α平行，∴u ⊥v ，即u ·v ＝0，∴1×3＋3×2＋z ×1＝0，∴z ＝－9.4．在三棱锥P －ABC 中，CP ，CA ，CB 两两垂直，AC ＝CB ＝1，PC ＝2，在如图所示的空间直角坐标系中，下列向量中是平面PAB 的法向量的是( )A.⎝⎛⎭⎪⎫1，1，12 B ．(1，2，1) C ．(1,1,1) D ．(2，－2,1) 答案 A解析 PA →＝(1,0，－2)，AB →＝(－1,1,0)，设平面PAB 的一个法向量为n ＝(x ，y,1)，则x －2＝0，即x ＝2；－x ＋y ＝0，即y ＝x ＝2.所以n ＝(2,2,1)．因为⎝⎛⎭⎪⎫1，1，12＝12n ，所以A正确．5．在棱长为1的正方体ABCD －A 1B 1C 1D 1中，M 为棱BB 1的中点，在棱DD 1上是否存在点P ，使MD ⊥平面PAC?解 如图，建立空间直角坐标系，则A (1,0,0)，C (0,1,0)，D (0,0,0)，M ⎝⎛⎭⎪⎫1，1，12.假设存在P (0,0，x )满足条件，则PA →＝(1,0，－x )，AC →＝(－1,1,0)．设平面PAC 的法向量为n ＝(x 1，y 1，z 1)，则由⎩⎪⎨⎪⎧ PA →·n ＝0，AC →·n ＝0，得⎩⎪⎨⎪⎧ x 1－xz 1＝0，－x 1＋y 1＝0.令x 1＝1得y 1＝1，z 1＝1x ，即n ＝⎝ ⎛⎭⎪⎫1，1，1x ， 由题意MD →∥n ，由MD →＝⎝⎛⎭⎪⎫－1，－1，－12，得x ＝2， ∵正方体棱长为1，且2>1，∴棱DD 1上不存在点P ，使MD ⊥平面PAC .。

3.2.3空间角的计算⑴【学习目标】能用向量方法解决线线，线面，面面的夹角的计算问题． 【学习重点】空间线线，线面，面面的夹角的计算用． 【学习难点】将几何中相关的量转化为坐标形式．【学习过程】 一．知识要点立体几何中角的计算是建立在弄清概念，恰当作图，严格论证的基础上的．空间的角有三种：异面直线所成的角；直线和平面所成的角；二面角．在学习了空间向量之后，我们可以用一种统一的模式来求以上各角． 1．异面直线所成的角设 l 1 与 l 2 为异面直线，a 1→ 与 a 2→分别为 l 1 与 l 2的方向向量，设l 1 与 l 2所成的角为θ，则有 cos θ = | cos < a 1→，a 2→> | = | a 1→·a 2→ || a 1→ |·| a 2→ |．2．直线和平面所成的角设 a → 为直线 l 的方向向量，n →为平面α的法向量，θ为 l 与平面 α 所成的角，则有cos (90°− θ) = | cos < a →，n →>| = | a →·n → || a → |·| n → |，即sin θ = | a →· n → || a → |·| n → |．3．平面与平面所成的角设二面角α − l − β 的两个半平面α，β的法向量分别是 n 1→ ，n 2→，二面角α − l− β 的大小为 θ ，则有| cos θ | = | n 1→ · n 2→ || n 1→ |·| n 2→ |．由于平面的法向量的选取的不同，有θ = < n 1→，n 2→ >，或θ = π− < n 1→，n 2→>．若可以确定二面角是锐角或钝角，则此二面角的大小可以唯一确定．综上，空间角的问题最终都转化为求直线夹角的问题，这样可以避免一些复杂的作图和证明过程，但在应用时要注意对结果的处理．二．例题讲解例1．棱长为1的正方体ABCD -A 1B 1C 1D 1中，P 为DD 1的中点，O 1，O 2，O 3分别是面A 1B 1C 1D 1，面BB 1C 1C ，面ABCD 的中心．求异面直线PO 3与O 1O 2所成角的余弦值．例2．在正方体ABCD -A 1B 1C 1D 1中，F 是BC 的中点，点E 1在D 1C 1上，且D 1E 1= 14D 1C 1，试求直线E 1F 与平面D 1AC 所成角的正弦值．变题:若将题中的条件“F 是BC 的中点”改为“CF = 14CB ”呢?D C B D 1 C 1 B 1A 1PO 3O 2 O 1 DCBAD1 C 1B 1A 1例3．已知E ，F 分别是正方体ABCD -A 1B 1C 1D 1的棱BC 和CD 的中点，求：⑴A 1D 与EF 所成角的大小； ⑵A 1F 与平面B 1EB 所成角的大小； ⑶二面角C-D 1B 1-B 的大小．三．课堂练习1．设a →，b →分别是两条异面直线l 1，l 2 的方向向量，且cos <a →，b →> = −12，则异面直线l 1，l 2所成的角的大小为 ．2．已知正方体ABCD -A 1B 1C 1D 1中，M 是AB 的中点，则对角线DB 1与CM 所成的角的余弦值 ． 3．已知平面的一条斜线和它在平面内的射影的夹角为45°，平面内一条直线和这条斜线在平面内的射影的夹角为45°，则斜线和平面内的这条直线所成的角的大小为 ． 四．课堂小结1．两条异面直线的所成的角等于两条直线的方向向量的夹角(或其补角)．要注意两条异面直线所成角的范围是锐角或直角，而两条直线的方向向量所成的角的范围是[0，π]，求解过程中要注意结果的处理；2．直线与平面所成的角等于直线与平面的法向量所成角的余角；DCBAD 1FEA 1C 1B 13．二面角的平面角的大小为等于两平面的法向量所成的角(或其补角)．若以二面角内的一点为起点向两个平面引射线(平面的法向量)，则两法向量所成的角与二面角的平面角互补；若以二面角外的一点为起点向两个平面引射线，则两法向量所成的角与二面角的平面角相等． 五．课后作业1： 1．已知二面角α−l −β为60°，异面直线a ，b 分别垂直于平面α ，β，则a ，b 所成的角的大小是 ． 2．在边长为a 的正三角形ABC 中，AD ⊥BC 于D ，沿AD 折成二面角B -AD -C 后，BC =12a ，这时二面角B -AD -C 的大小为 ． 3．正方体ABCD -A 1B 1C 1D 1中，E ，F 分别是AA 1，A 1D 1的中点，则EF 与面A 1C 1所成的角是 ． 4．已知锐二面角α−l −β的平面角是θ，m 是平面α内异于l 的一条直线，则m 与β所成的角的范围是 ．5．在正方体ABCD -A 1B 1C 1D 1中，求A 1B 与A 1B 1CD 平面所成角的大小． 求二面角B -PA -C 的大小． 6．在四棱锥V -ABCD 中，底面ABCD 是正方形，侧面VAD 是正三角形，平面VAD ⊥底面ABCD ．⑴证明：AB ⊥平面VAD ；⑵求平面VAD 与面VDB 所成的二面角的大小．A BCDV。

321直线的方向向量与平面的法向量【学习目标】1. 掌握平面的法向量的概念及性质，理解平面的向量表示，掌握直线与平面垂直的判定定理,能够由条件证明直线与平面垂直.2. 理解掌握两个平面平行或垂直的条件，能够利用向量的平行或垂直的条件证明两个平面平行或垂直.【学习重点】平面法向量的概念.【学习难点】平面法向量的理解及灵活应用.【学习过程】一•知识要点1. 直线的方向向量_____________________ 的向量叫做直线l的方向向量.2. 平面法向量的概念_______________________________________________________ ，那么称向量Tn垂直于平面a，记作F丄a .此时，我们把向量T叫做平面a的法向量. 说明：⑴平面的一个法向量垂直于与平面a共面的所有向量；⑵一个平面的所有法向量平行.3. 平面法向量的表示式A是空间任一点，F为空间任一非零向量，则^M・rT = 0表示通过空间内一点A 并且与一个向量~n垂直的平面.说明：⑴满足天M - ~n = 0的点M的轨迹是一个与向量~n垂直的平面.⑵若nT, n?分别是平面a ,卩的法向量，贝y a//卩或a与卩重合nT // nJ ；a 丄卩n i 丄n2 n i - n2 = 0 .二.基础训练1. __________________________________________________________________________ 已知A(1 ,0, 1), B(0 , 1, 1) , C(1 , 1, 0),则平面ABC的—个法向量是 __________________这个法向量的单位向量是2. 平面 a 的一个法向量为 n i = (1 , 2, 1)，平面 卩的一个法向量为 n 2 = -(3 , 4, 2),则平面a 与平面卩的位置关系是 ______________________ .3. ________________________________________________________________ 已知向量"OA = (1 , 1, -1)，与"OA 平行的单位向量是 _____________________________________ .4. ______________________________________________________________________ 原点0在平面 a 上的射影为P (2 , 9,-6)，则平面a 的方程为 ________________________________ .三.例题讲解例1.如图，点E 为矩形ABCD 所在平面外一点，且 AE !平面ABCD 已知△ EAD 是等腰三 角形，F , G 分别是AB EC 的中点.2. 已知正方形 ABCD 和矩形ACEF 所在的平面互相垂直,的中点.求证:(1) AM/平面 BDE (2) AM 丄平面 BDF 求证："G 是平面ECD 的法向量.AB = 2, AF = 1 , M 是线段 EF例3.求通过点R(3 , 1, -1) , P2(1 , -1, 0)，且平行于 "=(-1, 0, 2)的平面.四•课堂练习1在空间直角坐标系中，下列向量中是平面xOz的法向量的是__________ •2. 平面a的一个法向量这(1 , 2, 0)，平面卩的一个法向量为(2 , -1 , 0)，则平面a与平面卩的位置关系是 ____________ .3. ______________________________________________________________ 已知向量"OA =(3 , 4, 12)，与"OA平行的单位向量"e是_________________________________ .五.课堂小结1 .一个平面的法向量，其实就是该平面的一条垂线上的方向向量；直线的方向向量和平面的法向量是不唯一的；2 .利用直线的方向向量和平面的法向量来解决空间的线、面的平行、垂直等问题的关键是确定合适的方向向量和法向量；3 .求直线的方向向量和平面的法向量，一般采用待定系数法.先设出向量，然后再利用向量的垂直或向量的平行等条件来确定法向量或方向向量；4. (A, B, C)是平面Ax +By + Cz + D = 0的一个法向量.六.课后作业1:1. 空间直角坐标系中，A(1 , 2, 3) , B(-1, 0, 5) , C(3 , 0, 4) , D4 , 1, 3)，则直线AB与CD的位置关系是___________ .2. 直线I的方向向量为"=(1 , -1 , 3)，平面a的法向量为"=(0 , 3, 1)，贝U I与a的关系是 ____________ .3. 已知三角形ABC的三顶点A(1 , -2, -3) , B(-1, -1, -1), C(0 , 0, -5)，则△ ABC的形状是 ________________ .4. 若两条异面直线的方向向量的夹角是_________ 150°,则这两条异面直线所成的角是.5. 空间直角坐标系中，设平面a经过点P(X o, y o, Z o),平面a的法向量为1^=(A, B, C), M(x,y，z)是平面a内任意一点，则x，y，z满足的关系式为________________________________ .6. __________________________________________________________________________ 在空间直角坐标系中，平面3x + 4y -12z +15=0的单位法向量是_____________________________ .7. 已知四棱锥&ABCD勺底面是直角梯形，/ AB(=90°, AD// BC SA1平面ABCD SA= AB1=BC=1 , AD=2，求平面SDC勺一个法向量.&在正方体ABCDA'BC D中，证明BD丄平面ACB.。

课时分层作业(二十八)(建议用时：40分钟)[基础达标练]一、选择题1．直线l 的方向向量s ＝(－1,1,1)，平面α的法向量为n ＝(2，x 2＋x ，－x )，若直线l ∥平面α，则x 的值为( )A ．－2B ．－ 2 C. 2 D ．± 2D [线面平行时，直线的方向向量垂直于平面的法向量，故－1×2＋1×(x 2＋x )＋1×(－x )＝0，解得x ＝± 2.]2．若直线l ∥平面α，直线l 的方向向量为s 、平面α的法向量为n ，则下列结论正确的是( )A ．s ＝(－1,0,2)，n ＝(1,0，－1)B ．s ＝(－1,0,1)，n ＝(1,2，－1)C ．s ＝(－1,1,1)，n ＝(1,2，－1)D ．s ＝(－1,1,1)，n ＝(－2,2,2)C [直线与平面平行，直线的方向向量和平面的法向量垂直，经检验只有选项C 中s·n ＝0，故选C.]3．设u ＝(－2,2，t )，v ＝(6，－4,4)分别是平面α，β的法向量．若α⊥β，则t ＝( )A ．3B ．4C ．5D ．6C [∵α⊥β，则u·v ＝－2×6＋2×(－4)＋4t ＝0，∴t ＝5.]二、填空题4．若AB →＝λCD →＋μCE →(λ，μ∈R)，则直线AB 与平面CDE 的位置关系是________．[解析] ∵AB →＝λCD →＋μCE →(λ，μ∈R)，∴AB →与CD →，CE →共面，∴AB ∥平面CDE 或AB ⊂平面CDE .[答案] AB ∥平面CDE 或AB ⊂平面CDE5．已知AB →＝(1,5，－2)，BC →＝(3,1，z )，若AB →⊥BC →，BP →＝(x －1，y ，－3)，且BP ⊥平面ABC ，则(x ，y ，z )等于________．[解析] AB →·BC →＝3＋5－2z ＝0，故z ＝4.BP →·AB →＝x －1＋5y ＋6＝0，且BP →·BC →＝3(x －1)＋y －12＝0，得x ＝407，y ＝－157.[答案] ⎝ ⎛⎭⎪⎫407，－157，4 6．如图，在正方体ABCD ­A 1B 1C 1D 1中，P 为A 1B 1上任意一点，则DP 与BC 1始终________(填“垂直”或“平行”)．[解析] 因为DP →·C 1B →＝(DA 1→＋A 1P →)·C 1B →＝(CB 1→＋A 1P →)·C 1B →＝CB 1→·C 1B →＋A 1P →·C 1B →＝A 1P →·C 1B →＝A 1P →·(C 1C →＋CB →)＝A 1P →·C 1C →＋A 1P →·CB →＝0，所以DP →⊥C 1B →，即DP 与BC 1始终垂直．[答案] 垂直7．已知点A (1，－2,11)，B (4,2,3)，C (6，－1,4)，则△ABC 的形状是________三角形．[解析] 求得AC →＝(5,1，－7)，BC →＝(2，－3,1)，因为AC →·BC →＝0，所以AC →⊥BC →，所以△ABC是直角三角形．[答案] 直角8．如图所示，在长方体ABCD ­A 1B 1C 1D 1中，AB ＝2，AA 1＝3，AD ＝22，P 为C 1D 1的中点，M 为BC 的中点，则AM 与PM 的位置关系为________．[解析] 以D 点为原点，分别以DA ，DC ，DD 1所在直线为x 轴，y 轴，z 轴，建立如图所示的空间直角坐标系D ­xyz ，依题意，可得D (0,0,0)，P (0,1，3)，C (0,2,0)，A (22，0,0)，M (2，2,0)．∴PM →＝(2，2,0)－(0,1，3)＝(2，1，－3)，AM →＝(2，2,0)－(22，0,0)＝(－2，2,0)，∴PM →·AM →＝(2，1，－3)·(－2，2,0)＝0，即PM →⊥AM →，∴AM ⊥PM .[答案] 垂直三、解答题9．已知四棱锥P ­ABCD 的底面是直角梯形，AB ∥DC ，∠DAB＝90°，PD ⊥底面ABCD ，且PD ＝DA ＝CD ＝2AB ＝2，M 点为PC 的中点．(1)求证：BM ∥平面PAD ；(2)在平面PAD 内找一点N ，使MN ⊥平面PBD .[解] (1)证明：因为PD ⊥底面ABCD ，CD ∥AB ，CD ⊥AD .所以以D 为坐标原点，建立空间直角坐标系D ­xyz (如图所示)．由于PD ＝CD ＝DA ＝2AB ＝2，所以D (0,0,0)，A (2,0,0)，B (2,1,0)，C (0,2,0)，P (0,0,2)，M (0,1,1)，所以BM →＝(－2，0,1)，DC →＝(0,2,0)，因为DC ⊥平面PAD ，所以DC →是平面PAD 的法向量，又因为BM →·DC →＝0，且BM ⊄平面PAD ，所以BM ∥平面PAD .(2)设N (x,0，z )是平面PAD 内一点，则MN →＝(x ，－1，z －1)，DP →＝(0,0,2)，DB →＝(2,1,0)，若MN ⊥平面PBD ，则⎩⎪⎨⎪⎧ 2z －1＝0，2x －1＝0，即⎩⎪⎨⎪⎧ x ＝12，z ＝1，所以在平面PAD 内存在点N ⎝ ⎛⎭⎪⎫12，0，1，使MN ⊥平面PBD .10．如图所示，在四棱锥P ­ABCD 中，PC ⊥平面ABCD ，PC ＝2，在四边形ABCD 中，∠B ＝∠C ＝90°，AB ＝4，CD ＝1，点M 在PB 上，PB ＝4PM ，PB 与平面ABCD 成30°的角．求证：(1)CM ∥平面PAD ；(2)平面PAB ⊥平面PAD .[证明] 以C 为坐标原点，CB 所在直线为x 轴，CD 所在直线为y 轴，CP 所在直线为z 轴，建立如图所示的空间直角坐标系C ­xyz .∵PC ⊥平面ABCD ，∴∠PBC 为PB 与平面ABCD 所成的角，∴∠PBC ＝30°.∵PC ＝2，∴BC ＝23，PB ＝4，∴D (0,1,0)，B (23，0,0)，A (23，4,0)，P (0,0,2)，M ⎝ ⎛⎭⎪⎫32，0，32， ∴DP →＝(0，－1,2)，DA →＝(23，3,0)，CM →＝⎝ ⎛⎭⎪⎫32，0，32， (1)法一：令n ＝(x ，y ，z )为平面PAD 的一个法向量，则⎩⎪⎨⎪⎧ DP →·n ＝0，DA →·n ＝0，即⎩⎨⎧ －y ＋2z ＝0，23x ＋3y ＝0，∴⎩⎪⎨⎪⎧ z ＝12y ，x ＝－32y ，令y ＝2，得n ＝(－3，2,1)．∵n ·CM →＝－3×32＋2×0＋1×32＝0， ∴n ⊥CM →，又CM ⊄平面PAD ，∴CM ∥平面PAD .法二：∵PD →＝(0,1，－2)，PA →＝(23，4，－2)，令CM →＝xPD →＋yPA →，则⎩⎪⎨⎪⎧ 32＝23y ，0＝x ＋4y ，32＝－2x －2y ，方程组有解为⎩⎪⎨⎪⎧ x ＝－1，y ＝14， ∴CM →＝－PD →＋14PA →，由共面向量定理知CM →与PD →，PA →共面．又∵CM ⊄平面PAD ，∴CM ∥平面PAD . (2)取AP 的中点E ，连接BE ，则E (3，2,1)，BE →＝(－3，2,1)，∵PB ＝AB ，∴BE ⊥PA .又∵BE →·DA →＝(－3，2,1)·(23，3,0)＝0，∴BE →⊥DA →，∴BE ⊥DA ，又PA ∩DA ＝A ，∴BE ⊥平面PAD .又∵BE ⊂平面PAB ，∴平面PAB ⊥平面PAD .[能力提升练]1．空间直角坐标系中，A (1,2,3)，B (－2，－1,6)，C (3,2,1)，D (4,3,0)，则直线AB 与CD 的位置关系是_____________________．[解析] 由题意得，AB →＝(－3，－3,3)，CD →＝(1,1，－1)，∴AB →＝－3CD →，∴AB →与CD →共线．又AB →与CD →没有公共点．∴AB ∥CD .[答案] 平行2.如图，四棱锥P ­ABCD 的底面ABCD 是边长为1的正方形，PD ⊥底面ABCD ，且PD ＝1，若E ，F 分别为PB ，AD 中点，则直线EF 与平面PBC 的位置关系________．[解析] 以D 为原点，DA ，DC ，DP 所在直线为x 轴，y 轴，z 轴建立空间直角坐标系(图略)，则E ⎝ ⎛⎭⎪⎫12，12，12， F ⎝ ⎛⎭⎪⎫12，0，0，∴EF →＝⎝ ⎛⎭⎪⎫0，－12，－12，平面PBC 的一个法向量n ＝(0,1,1)．∵EF →＝－12n ，∴EF →∥n ， ∴EF ⊥平面PBC .[答案] 垂直3．已知空间两点A (－1,1,2)，B (－3,0,4)，直线l 的方向向量为a ，若|a |＝3，且直线l 与直线AB 平行，则a ＝________.[解析] 设a ＝(x ，y ，z )，∵AB →＝(－2，－1,2)，且l 与AB 平行，∴a ∥AB →，∴x －2＝y －1＝z 2，∴x ＝2y ，z ＝－2y . 又∵|a |＝3，∴|a |2＝x 2＋y 2＋z 2＝4y 2＋y 2＋4y 2＝9，∴y ＝±1，∴a ＝(2,1，－2)或(－2，－1,2)．[答案] (2,1，－2)或(－2，－1,2)4．如图所示，在梯形ABCD 中，AB ∥CD ，AD ＝DC ＝CB ＝a ，∠ABC ＝60°，平面ACFE ⊥平面ABCD ，四边形ACFE 是矩形，AE ＝a ，点M 在线段EF 上．当EM 为何值时，AM ∥平面BDF ？证明你的结论．[解] 法一：当EM ＝33a 时，AM ∥平面BDF ，以点C 为原点，CA ，CB ，CF 所在直线为坐标轴，建立空间直角坐标系(图略)，则C (0,0,0)，B (0，a,0)，A (3a,0,0)，D ⎝ ⎛⎭⎪⎫3a 2，－12a ，0，F (0,0，a )，E (3a,0，a )，因为AM ⊄平面BDF ，所以AM ∥平面BDF ⇔AM →与FB →，FD →共面，所以存在实数m ，n ，使AM →＝mFB →＋nFD →，设EM →＝tEF →.因为EF →＝(－3a,0,0)，EM →＝(－3at,0,0)，所以AM →＝AE →＋EM →＝(－3at,0，a )，又FD →＝⎝ ⎛⎭⎪⎫32a ，－12a ，－a ，FB →＝(0，a ，－a )，从而(－3at,0，a )＝m (0，a ，－a )＋n ⎝ ⎛⎭⎪⎫32a ，－12a ，－a 成立，需⎩⎪⎨⎪⎧ －3at ＝32an ，0＝ma －12an ，a ＝－am －an ，解得t ＝13， 所以当EM ＝33a 时，AM ∥平面BDF . 法二：当EM ＝33a 时，AM ∥平面BDF ，在梯形ABCD 中， 设AC ∩BD ＝N ，连接FN ，则CN ∶NA ＝1∶2，因为EM ＝33a ， 而EF ＝AC ＝3a ，所以EM ∶MF ＝1∶2，所以MF綊AN，所以四边形ANFM是平行四边形，所以AM∥NF，又因为NF⊂平面BDF，AM⊄平面BDF，所以AM∥平面BDF.。

空间向量与立体几何【学习目标】正确理解空间向量的有关概念、性质和定理，正确理解并记住各定理及公式的条件和结论，正确地选用基底或适当地建立坐标系，以向量为工具通过向量的运算解决问题． 【学习过程】 一．知识扫描1．空间线与面的平行与垂直设空间两条直线l 1，l 2的方向向量为 e 1→，e 2→，平面α，β的法向量分别是 n 1→，n 2→，则有：2．判定三点共线及四点共面主要依据空间向量的共线定理与共面定理，即如果非零向量a →，b →共线，则必存在唯一的实数λ，使得b →=λa →．如果三个非零向量a →，b →，c →共面，则必存在一对实数λ，μ，使得c →=λa →+μb →． 由上可得以下结论：⑴空间三点A ，B ，C 共线的条件是：存在实数λ或μ，使得OC → = 11 +λ OA →+ λ1 +λ OB →或OC → = λ OA →+ μ OB →(λ + μ =1)．⑵空间四点A ，B ，C ，D 无三点共线，则它们共面的充要条件是：存在唯一一对实数x ，y ，z ，使得AD →= x AB → +y AC → 或OD → = x OA →+ y OB → +z OC →(x + y + z =1)．3．空间的角异面直线所成的角，直线与平面所成的角，两平面所成的角均可以由直线的法向量与平面的法向量求得，但最终结果必须符合所求角的范围，否则要改成它的补角或余角． 二．例题讲解例1．如图，在直三棱柱ABC -A 1B 1C 1中，AC =3，BC =4，AB =5，AA 1=4，点D 是AB 的中点． ⑴求证：AC ⊥BC 1；⑵求证：AC 1∥平面CDB 1．例2．在四棱锥P -ABCD 中，PD ⊥平面ABCD ，又四边形ABCD 是矩形，AD =2，DC =1，PD =1，M ，N 分别是AD ，PB 的中点． ⑴求证：P B ⊥MN ；⑵求证：平面MNC ⊥平面PBC ． ADBCC 1A 1B 1ABCD P NM例3．如图，四棱锥P -ABCD 中，ABCD 为平行四边形，E ∈PC ，PE = 13PC ，F ∈PB ，PF = 23PB ，R ∈PD ，PR = 23PD ，求证：PA ∥面EFR ．例4．已知斜三棱柱ABC -A 1B 1C 1中，AC =AB ，∠BAC = 90°，侧棱与底面成60°角，BC 1 = 26，BC 1⊥AC ，求三棱柱ABC -A 1B 1C 1的体积．1三．课堂小结1．用空间向量的方法解决立体几何问题，关键在于依托图形建立空间直角坐标系或恰当地选取基向量，将其它向量用坐标或基向量表示，进行适当的运算．2．求角的问题：⑴求两直线所成的角，可以先找出这两直线方向向量，然后通过向量的运算求出两方向向量的夹角即为两直线的夹角；若求出的不是锐角或直角，还要根据两直线所成的角不超过90°，取其补角；⑵求直线与平面所成的角，一般改成求直线与平面的法向量所成的角，这两个角是互余关系；⑶求两平面所成的角，一般找出两平面的法向量，先求出两法向量所成的角，再根据二面角的特点确定其平面角与两法向量所成的角相等或互补． 四．课后作业1:1．对空间任意两个向量a →，b →(b →≠0→)，a →∥b →的充要条件是( ) A ．a → = b → B ．a → = −b → C ．b → = λa → D ．a → = λb →2．已知向量a → = (0，2，1)，b → = (−1，1，−2)，则 a → 与 b →的夹角为 ． 3．在棱长为1的正方体ABCD —A 1B 1C 1D 1中，M 和N 分别为A 1B 1和BB 1的中点，那么直线AM与CN 所成角的余弦值是 ．4．正方体ABCD -A 1B 1C 1D 1中，E 是棱AB 的中点，且AB =1，则EC 与平面A 1B 1CD 所成角的正弦值为 ．5．如图：ABCD 为矩形，PA ⊥平面ABCD ，PA =AD ，M 、N 分别是PC 、AB 中点， 求证：MN ⊥平面PCD ．6．如图，正四棱锥S —ABCD 中，所有棱长都是2，P 为SA 的中点．⑴求二面角B —SC —D 的余弦值；⑵如果点Q 在棱SC 上，那么直线BQ 与PD 能否垂直？请说明理由．A BCDPMNABCDSPQ。

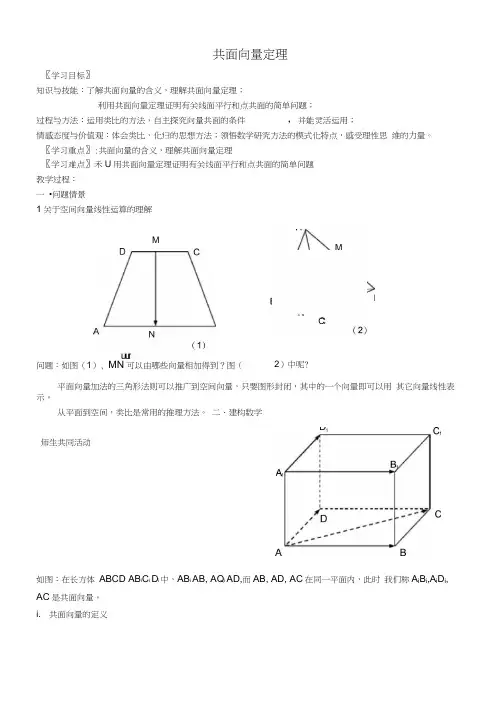
共面向量定理〖学习目标〗知识与技能：了解共面向量的含义，理解共面向量定理；利用共面向量定理证明有关线面平行和点共面的简单问题；过程与方法：运用类比的方法，自主探究向量共面的条件，并能灵活运用；情感态度与价值观：体会类比，化归的思想方法；领悟数学研究方法的模式化特点，感受理性思 维的力量。

〖学习重点〗:共面向量的含义，理解共面向量定理〖学习难点〗禾U 用共面向量定理证明有关线面平行和点共面的简单问题教学过程： 一 •问题情景1关于空间向量线性运算的理解问题：如图（1）, MN 可以由哪些向量相加得到？图（平面向量加法的三角形法则可以推广到空间向量，只要图形封闭，其中的一个向量即可以用 其它向量线性表示。

从平面到空间，类比是常用的推理方法。

二、建构数学师生共同活动如图：在长方体 ABCD AB i C i D i 中，AB i AB, AQ i AD,而AB, AD, AC 在同一平面内，此时 我们称A i B i ,A i D i ,AC 是共面向量。

i. 共面向量的定义2）中呢?MC一般地， ______________________________________ 叫共面向量。

类比1:共面向量与共线向量的定义在形式上有何相同之处 ？都是将向量问题转化为直线与直线或直线与平面之间的位置关系来研究探究1:(1) 我们已经知道空间中任意两个向量一定可以共面，那么空间中任意三个向量一定是共面向量吗？请举例说明. 结论：空间中的任意三个向量不一定是共面向量. 例如：对于四面体 ABCDuuu uu u uu u rAB 、AC 、AD 这三个向量就不是共面向量.(2) 空间三个向量p , a,b 具备怎样的条件时才是共面向量呢? 2. 共面向量的判定在平面向量中，向量 b 与非零向量a 共线的充要条件是 _________________________________ .联想：空间任意一个向量p 与两个不共线向量 a, b 共面时，它们之间存在怎样的关系呢?类比到空间向量，探究得到,而且在本质上也是一致a,b 都可以平移到同一个平面 ，当a,b 不共线时，可以作为基向量，现它们距离地面 CDE 的高度一样，你能告诉它们这是为什么吗?的.这是因为任意两个空间向量 向量p 与它们共面，也就是向量 p 可以平移到这个平面，所以就能用a,b 线性表示.三、数学运用问题：如图，已知两堵矩形墙壁ABCD 和ADEF 所在平面垂直于地面, 沿对角线BD ，AE 向上爬，当它们分别爬到 M ，N 处时，此时BM有两只蚂蚁分别从D 、E 两点11BD ，AN AE.它们惊奇的发 3 - 共面向量定理如果两个向量a ，b 不共线，那么向量 p 与向量a ，b 共面的充要条件分析定理类比2:空间共线向量定理和平面共线定理是相同的 ，那么，空间共面向量定理是否和平面向量的某个定理相联系呢？空间向量中的共面定理与平面向量基本定理不仅在形式上是相同的思考：你能用综合法来证明吗？试比较这两种方法的差异。

3．2.1 直线的方向向量及平面的法向量1．用向量表示直线的位置条件直线l上一点A表示直线l方向的向量a(即直线l的□01方向向量)形式在直线l上取AB→＝a，那么对于直线l上任意一点P，一定存在实数t使得AP→＝□02tAB→作用定位置点A和向量a可以确定直线的位置定点可以具体表示出l上的任意一点(1)通过平面α上的一个定点和两个向量来确定条件平面α内两条□03相交直线的方向向量a，b和交点O形式对于平面α上任意一点P，存在有序实数对(x，y)，使得OP→＝□04x a＋y b(2)通过平面α上的一个定点和法向量来确定平面的法向量□05直线l⊥α，直线l的方向向量，叫做平面α的法向量确定平面位置过点A，以向量a为法向量的平面是完全确定的3．空间中平行、垂直关系的向量表示设直线l，m的方向向量分别为a，b，平面α，β的法向量分别为u，v，则线线平行l∥m⇔□06a∥b⇔□07a＝k b(k∈R)线面平行l∥α⇔□08a⊥u⇔□09a·u＝0面面平行α∥β⇔□10u∥v⇔□11u＝k v(k∈R)线线垂直 l ⊥m ⇔□12a ⊥b ⇔□13a ·b ＝0 线面垂直 l ⊥α⇔□14a ∥u ⇔□15a ＝λu (λ∈R ) 面面垂直 α⊥β⇔□16u ⊥v ⇔□17u ·v ＝01．判一判(正确的打“√”，错误的打“×”)(1)直线上任意两个不同的点A ，B 表示的向量AB →都可作为该直线的方向向量．( ) (2)若向量n 1，n 2为平面α的法向量，则以这两个向量为方向向量的两条不重合直线一定平行．( )(3)若平面外的一条直线的方向向量与平面的法向量垂直，则该直线与平面平行．( ) (4)若两条直线平行，则它们的方向向量的方向相同或相反．( ) 答案 (1)√ (2)√ (3)√ (4)√ 2．做一做(请把正确的答案写在横线上)(1)若点A (－1,0,1)，B (1,4,7)在直线l 上，则直线l 的一个方向向量的坐标可以是________．(2)已知a ＝(2，－4，－3)，b ＝(1，－2，－4)是平面α内的两个不共线向量．如果n ＝(1，m ，n )是α的一个法向量，那么m ＝________，n ＝________.(3)(教材改编P 104T 2)设平面α的法向量为(1,3，－2)，平面β的法向量为(－2，－6，k )，若α∥β，则k ＝________.(4)已知直线l 1，l 2的方向向量分别是v 1＝(1,2，－2)，v 2＝(－3，－6,6)，则直线l 1，l 2的位置关系为________．答案 (1)(2,4,6) (2)120 (3)4 (4)平行探究1 点的位置向量与直线的方向向量例1 (1)若点A ⎝ ⎛⎭⎪⎫－12，0，12，B ⎝ ⎛⎭⎪⎫12，2，72在直线l 上，则直线l 的一个方向向量为( )A.⎝ ⎛⎭⎪⎫13，23，1B.⎝ ⎛⎭⎪⎫13，1，23C.⎝ ⎛⎭⎪⎫23，13，1D.⎝ ⎛⎭⎪⎫1，23，13(2)已知O 为坐标原点，四面体OABC 的顶点A (0,3,5)，B (2,2,0)，C (0,5,0)，直线BD ∥CA ，并且与坐标平面xOz 相交于点D ，求点D 的坐标．[解析] (1)AB →＝⎝ ⎛⎭⎪⎫12，2，72－⎝ ⎛⎭⎪⎫－12，0，12＝(1,2,3)，⎝ ⎛⎭⎪⎫13，23，1＝13(1,2,3)＝13AB →，又因为与AB →共线的非零向量都可以作为直线l 的方向向量．故选A.(2)由题意可设点D 的坐标为(x,0，z )， 则BD →＝(x －2，－2，z )，CA →＝(0，－2,5)．∵BD ∥CA ，∴⎩⎪⎨⎪⎧x －2＝0，z ＝5，∴⎩⎪⎨⎪⎧x ＝2，z ＝5，∴点D 的坐标为(2,0,5)． [答案] (1)A (2)见解析 拓展提升求点的坐标：可设出对应点的坐标，再利用点与向量的关系，写出对应向量的坐标，利用两向量平行的充要条件解题．【跟踪训练1】 已知点A (2,4,0)，B (1,3,3)，在直线AB 上有一点Q ，使得AQ →＝－2QB →，求点Q 的坐标．解 由题设AQ →＝－2QB →，设Q (x ，y ，z )，则(x －2，y －4，z )＝－2(1－x,3－y,3－z )，∴⎩⎪⎨⎪⎧x －2＝－2(1－x )，y －4＝－2(3－y )，z ＝－2(3－z )，解得⎩⎪⎨⎪⎧x ＝0，y ＝2，∴Q (0，2，6).z ＝6，探究2 求平面的法向量例2 如图，ABCD 是直角梯形，∠ABC ＝90°，SA ⊥平面ABCD ，SA ＝AB ＝BC ＝1，AD ＝12，求平面SCD 与平面SBA 的法向量．[解]∵AD ，AB ，AS 是三条两两垂直的线段，∴以A 为原点，分别以AD →，AB →，AS →的方向为x 轴、y 轴、z 轴的正方向建立坐标系，则A (0,0,0)，D ⎝ ⎛⎭⎪⎫12，0，0，C (1,1,0)，S (0,0,1)，AD →＝⎝ ⎛⎭⎪⎫12，0，0是平面SAB 的法向量，设平面SCD 的法向量n ＝(1，λ，u )，则n ·DC →＝(1，λ，u )·⎝ ⎛⎭⎪⎫12，1，0＝12＋λ＝0，∴λ＝－12.n ·DS →＝(1，λ，u )·⎝ ⎛⎭⎪⎫－12，0，1＝－12＋u ＝0，∴u ＝12，∴n ＝⎝⎛⎭⎪⎫1，－12，12. 综上，平面SCD 的一个方向向量为n ＝⎝⎛⎭⎪⎫1，－12，12，平面SBA 的一个法向量为AD →＝⎝ ⎛⎭⎪⎫12，0，0.拓展提升设直线l 的方向向量为u ＝(a 1，b 1，c 1)，平面α的法向量v ＝(a 2，b 2，c 2)，则l ⊥α⇔u ∥v ⇔u ＝k v ⇔a 1＝ka 2，b 1＝kb 2，c 1＝kc 2，其中k ∈R ，平面的法向量的求解方法：①设出平面的一个法向量为n ＝(x ，y ，z )．②找出(或求出)平面内的两个不共线的向量的坐标：a ＝(a 1，b 1，c 1)，b ＝(a 2，b 2，c 2)．③依据法向量的定义建立关于x ，y ，z 的方程组⎩⎪⎨⎪⎧n ·a ＝0，n ·b ＝0.④解方程组，取其中的一个解，即得法向量，由于一个平面的法向量有无数多个，故可在方程组的解中取一个最简单的作为平面的法向量．【跟踪训练2】 在正方体ABCD －A 1B 1C 1D 1中，求证：DB 1→是平面ACD 1的一个法向量．证明 设正方体的棱长为1，分别以DA →，DC →，DD 1→为单位正交基底建立如图所示的空间直角坐标系，则DB 1→＝(1,1,1)，AC →＝(－1,1,0)，AD 1→＝(－1,0,1)．于是有DB 1→·AC →DB 1→⊥AC →，即DB 1⊥AC . 同理，DB 1⊥AD 1，又AC ∩AD 1＝A ，所以DB 1⊥平面ACD 1，从而是平面ACD 1的一个法向量． 探究3 利用方向向量、法向量判断线、面 关系例3 (1)设a ，b 分别是不重合的直线l 1，l 2的方向向量，根据下列条件判断l 1与l 2的位置关系：①a ＝(2,3，－1)，b ＝(－6，－9,3)； ②a ＝(5,0,2)，b ＝(0,4,0)； ③a ＝(－2,1,4)，b ＝(6,3,3)．(2)设u ，v 分别是不同的平面α，β的法向量，根据下列条件判断α，β的位置关系： ①u ＝(1，－1,2)，v ＝⎝ ⎛⎭⎪⎫3，2，－12；②u ＝(0,3,0)，v ＝(0，－5,0)； ③u ＝(2，－3,4)，v ＝(4，－2,1)．(3)设u 是平面α的法向量，a 是直线l 的方向向量(l ⊄α)，根据下列条件判断α和l 的位置关系：①u ＝(2,2，－1)，a ＝(－3,4,2)； ②u ＝(0,2，－3)，a ＝(0，－8,12)； ③u ＝(4,1,5)，a ＝(2，－1,0)．[解] (1)①因为a ＝(2,3，－1)，b ＝(－6，－9,3)，所以a ＝－13b ，所以a ∥b ，所以l 1∥l 2.②因为a ＝(5,0,2)，b ＝(0,4,0)，所以a ·b ＝0， 所以a ⊥b ，所以l 1⊥l 2.③因为a ＝(－2,1,4)，b ＝(6,3,3)，所以a 与b 不共线，也不垂直，所以l 1与l 2的位置关系是相交或异面．(2)①因为u ＝(1，－1,2)，v ＝⎝⎛⎭⎪⎫3，2，－12，所以u ·v ＝3－2－1＝0，所以u ⊥v ，所以α⊥β.②因为u ＝(0,3,0)，v ＝(0，－5,0)，所以u ＝－35v ，所以u ∥v ，所以α∥β.③因为u ＝(2，－3,4)，v ＝(4，－2,1)．所以u 与v 既不共线，也不垂直，所以α，β相交．(3)①因为u ＝(2,2，－1)，a ＝(－3,4,2)，所以u ·a ＝－6＋8－2＝0， 所以u ⊥a ，所以直线l 和平面α的位置关系是l ∥α.②因为u ＝(0,2，－3)，a ＝(0，－8,12)，所以u ＝－14a ，所以u ∥a ，所以l ⊥α.③因为u ＝(4,1,5)，a ＝(2，－1,0)，所以u 和a 不共线也不垂直，所以l 与α斜交． 拓展提升利用向量判断线、面关系的方法(1)两直线的方向向量共线(垂直)时，两直线平行(垂直)；否则两直线相交或异面． (2)直线的方向向量与平面的法向量共线时，直线和平面垂直；直线的方向向量与平面的法向量垂直时，直线在平面内或线面平行；否则直线与平面相交但不垂直．(3)两个平面的法向量共线(垂直)时，两平面平行(垂直)；否则两平面相交但不垂直．【跟踪训练3】 根据下列条件，判断相应的线、面位置关系： (1)直线l 1，l 2的方向向量分别为a ＝(1，－3，－1)，b ＝(8,2,2)； (2)平面α，β的法向量分别是u ＝(1,3,0)，v ＝(－3，－9，0)；(3)直线l 的方向向量，平面α的法向量分别是a ＝(1，－4，－3)，u ＝(2,0,3)； (4)直线l 的方向向量，平面α的法向量分别是a ＝(3,2,1)，u ＝(－1,2，－1)． 解 (1)因为a ＝(1，－3，－1)，b ＝(8,2,2)，所以a ·b ＝8－6－2＝0，所以a ⊥b ，所以l 1⊥l 2.(2)因为u ＝(1,3,0)，v ＝(－3，－9,0)，所以v ＝－3u ，所以v ∥u ，所以α∥β. (3)因为a ＝(1，－4，－3)，u ＝(2,0,3)，所以a ≠k u (k ∈R )且a ·u ≠0，所以a 与u 既不共线也不垂直，即l 与α相交但不垂直．(4)因为a ＝(3,2,1)，u ＝(－1,2，－1)，所以a ·u ＝－3＋4－1＝0，所以a ⊥u ，所以l ⊂α或l ∥α.1.空间中一条直线的方向向量有无数个.2.线段中点的向量表达式：对于AP →＝tAB →，当t ＝12时，我们就得到线段中点的向量表达式．设点M 是线段AB 的中点，则OM →＝12(OA →＋OB →)，这就是线段AB 中点的向量表达式.，求出向量的横、纵、竖坐标是具有某种关系的，而不是具体的值，可设定某个坐标为常数，再表示其他坐标.(1)设n 是平面α的一个法向量，v 是直线l 的方向向量，则v ⊥n 且l 上至少有一点A ∉α，则l ∥α.(2)根据线面平行的判定定理：“如果平面外直线与平面内的一条直线平行，那么这条直线和这个平面平行”，要证明一条直线和一个平面平行，也可以在平面内找一个向量与已知直线的方向向量是共线向量.(3)根据共面向量定理可知，如果一个向量和两个不共线的向量是共面向量，那么这个向量与这两个不共线向量确定的平面必定平行，因此要证明平面外一条直线和一个平面平行，只要证明这条直线的方向向量能够用平面内两个不共线向量线性表示即可.(1)在一个平面内找到两个不共线的向量都与另一个平面的法向量垂直，那么这两个平面平行.(2)利用平面的法向量，证明面面平行，即如果a ⊥平面α，b ⊥平面β，且a ∥b ，那么α∥β.1．若平面α，β的法向量分别为a ＝⎝ ⎛⎭⎪⎫12，－1，3，b ＝(－1,2，－6)，则( ) A ．a ∥β B ．α与β相交但不垂直 C ．α⊥β D ．α∥β或α与β重合 答案 D解析 ∵b ＝－2a ，∴b ∥a ，∴α∥β或α与β重合．2．在长方体ABCD －A 1B 1C 1D 1中，AB ＝BC ＝2，AA 1＝2，E ，F 分别是平面A 1B 1C 1D 1，平面BCC 1B 1的中心，以点A 为原点，建立如图所示的空间直角坐标系，则直线EF 的方向向量可以是( )A.⎝ ⎛⎭⎪⎫1，0，22B ．(1,0，2) C ．(－1,0，2) D ．(2,0，－2) 答案 D解析 由已知得E (1,1，2)，F ⎝ ⎛⎭⎪⎫2，1，22，所以|EF →|＝⎝⎛⎭⎪⎫2，1，22－(1,1，2)＝⎝⎛⎭⎪⎫1，0，－22，结合选项可知，直线EF 的方向向量可以是(2,0，－2)．3．已知A (1,0,0)，B (0,1,0)，C (0,0,1)，则平面ABC 的一个单位法向量是( ) A.⎝⎛⎭⎪⎫33，33，－33 B.⎝ ⎛⎭⎪⎫33，－33，33 C.⎝ ⎛⎭⎪⎫－33，33，33 D.⎝ ⎛⎭⎪⎫－33，－33，－33 答案 D解析 由AB →＝(－1,1,0)，AC →＝(－1,0,1)，结合选项，验证知应选D.4．若直线l ∥α，且l 的方向向量为(2，m,1)，平面α的法向量为⎝ ⎛⎭⎪⎫1，12，2，则m ＝________.答案 －8解析 因为直线l ∥α，所以直线l 的方向向量与平面α的法向量垂直，所以(2，m,1)·⎝⎛⎭⎪⎫1，12，2＝2＋m 2＋2＝0，解得m ＝－8.5．在正方体ABCD －A 1B 1C 1D 1中，P 是DD 1的中点，O 为底面ABCD 的中心，求证：OB →1是平面PAC 的法向量．证明 建立空间直角坐标系如右图所示，不妨设正方体的棱长为2，则A (2,0,0)，P (0,0,1)，C (0,2,0)，B 1(2,2,2)，O (1,1,0)，于是OB 1→＝(1,1,2)，AC →＝(－2,2,0)，AP →＝(－2，0,1)，∴OB 1→·AC →＝－2＋2＝0，OB 1→·AP →＝－2＋2＝0. ∴OB 1→⊥AC →，OB 1→⊥AP →，即OB 1⊥AC ，OB 1⊥AP . ∵AC ∩AP ＝A ，∴OB 1⊥平面PAC ，即OB 1→是平面PAC 的法向量．。

空间向量的数量积（1）学习目的：⒈掌握空间向量夹角和模的概念及表示方法；⒉掌握两个向量数量积的概念、性质和计算方法及运算律；⒊掌握两个向量数量积的主要用途，会用它解决立体几何中的一些简单问题． 学习重点：两个向量的数量积的计算方法及其应用． 学习难点：两个向量数量积的几何意义． 学习过程： 一、复习引入 二、讲解新课1.空间向量的夹角及其表示已知两非零向量,a b rr ， 则AOB ∠叫做向量a r 与b r 的夹角，记作,a b <>rr ；规定0,a b π≤<>≤r r ,显然有,,a b b a <>=<>rr r r ；若,2a b π<>=rr ，则称a r 与b r 互相垂直，记作：a b ⊥r r .2.向量的模设OA a =ru u r，则 叫做向量a r 的长度或模，记作：||a r. 3.向量的数量积已知向量,a b r r ，则||||cos ,a b a b ⋅⋅<>r r r r 叫做,a b rr 的数量积，记作a b ⋅r r ，即a b ⋅=rr ．已知向量AB a =u u u r r 和轴l ，e r是l 上与l 同方向的单位向量，作点A 在l 上的射影A '，作点B 在l 上的射影B '，则A B ''u u u u r 叫做向量AB u u u r 在轴l 上或在e r上的正射影.可以证明A B ''u u u u r 的长度||||cos ,||A B AB a e a e ''=<>=⋅u u u u r u u u r r r r r ．4.数量积的坐标表示若),,(),,,(222111z y x b z y x a ==，有332211y x y x y x b a ++=⋅, 5.空间向量数量积的性质 （1）||cos ,a e a a e ⋅=<>r r r r r（2）0a b a b ⊥⇔⋅=r r r r （3）2||a a a =⋅r r r ．（4）212121||z y x a ++=6.空间向量数量积运算律（1）()()()a b a b a b λλλ⋅=⋅=⋅rrrrr r． （2） （交换律）．（3） （分配律）． 三、讲解范例：例 1.（1）已知23||,4||==,.12=⋅求,的夹角<,>.例2．如图,已知四棱柱1111D C B A ABCD -底面ABCD 是矩形5,3,41===AA AD AB ∠=1BAA ∠0160=DAA ,求1AC 的长.ABCD A 1B 1C 1D 1例3如图，在空间四边形OABC 中，8OA =,6AB =，4AC =，5BC =，45OAC ∠=o ，60OAB ∠=o ，求OA 与BC 的夹角的余弦值.说明:由图形知向量的夹角时易出错，如,135OA AC <>=ou u r u u u r易错写成,45OA AC <>=ou u r u u u r例4．已知空间四边形ABCD 中，AB CD ⊥，AC BD ⊥，求证：AD BC ⊥．说明：用向量解几何题的一般方法：把线段或角度转化为向量表示，并用已知向量表示未知向量，然后通过向量运算去计算或证明四、课堂练习：教材94页练习1-3五、小结 ：由于空间任意两个向量都可以转化为共面向量，所以空间两个向量的夹角的定义、取值范围、两个向量垂直的定义和表示符号及向量的模的概念和表示符号，两个向量的数量积的意义等，都与平面向量是相同的． 六、作业：1．已知空间四边形ABCD ，则AB →·CD →+BC →·AD →+CA →·BD →= 。

【关键字】空间3．2.2 空间线面关系的判定(二)垂直关系[学习目标] 1.会利用平面法向量证明两个平面笔直.2.能利用直线的方向向量和平面的法向量判定并证明空间中的笔直(线线、线面、面面)关系．知识点空间笔直关系的向量表示1．用向量法如何证明线面笔直？答案证直线的方向向量与平面的法向量平行．2．平面α上的向量a与平面β上的向量b笔直，能判断α⊥β吗？答案不能．题型一证明线线笔直问题例1 如图，△ABC和△BCD所在平面互相笔直，且AB＝BC＝BD＝2，∠ABC＝∠DBC＝120°，E，F分别为AC，DC的中点．求证：EF⊥BC.证明由题意，以点B为坐标原点，在平面DBC内过点B作笔直于BC的直线为x轴，BC所在直线为y轴，在平面ABC内过点B作笔直BC的直线为z轴，建立如图所示的空间直角坐标系，易得B(0,0,0)，A(0，－1，)，D(，－1,0)，C(0,2,0)，因而E(0，，)，F(，，0)，所以＝(，0，－)，＝(0,2,0)，因此·＝0.从而⊥，所以EF⊥BC.反思与感悟证明两直线笔直的基本步骤：建立空间直角坐标系→写出点的坐标→求直线的方向向量→证明向量笔直→得到两直线笔直．跟踪训练1 如图所示，在四棱锥P－ABCD中，PA⊥底面ABCD，垂足为A，AB⊥AD于A，AC⊥CD于C，∠ABC＝60°，PA＝AB＝BC，E是PC的中点．求证AE⊥CD.证明以A为坐标原点建立空间直角坐标系，设PA＝AB＝BC＝1，则A(0,0,0)，P(0,0,1)．∵∠ABC＝60°，∴△ABC为正三角形．∴C(，，0)，E(，，)．设D(0，y,0)，由AC⊥CD得·＝0，即y＝，则D(0，，0)，∴＝(－，，0)．又＝(，，)，∴·＝－×＋×＝0，∴⊥，即AE⊥CD.题型二证明线面笔直问题例2 如图所示，在正方体ABCDA1B1D1中，E，F分别是BB1，D1B1的中点．求证：EF⊥平面B.证明方法一设正方体的棱长为2，建立如图所示的空间直角坐标系，则A(2,0,0)，C(0,2,0)，B1(2,2,2)，E(2,2,1)，F(1,1,2)．∴＝(1,1,2)－(2,2,1)＝(－1，－1，1)．＝(2,2,2)－(2,0,0)＝(0,2,2)，＝(0,2,0)－(2,0,0)＝(－2,2,0)．而·＝(－1，－1,1)·(0,2,2)＝(－1)×0＋(－1)×2＋1×2＝0.·＝(－1，－1,1)·(－2,2,0)＝2－2＋0＝0，∴EF⊥AB1，EF⊥AC.又AB1∩AC＝A，AB1⊂平面B，AC⊂平面B，∴EF⊥平面B.方法二设＝a，＝c，＝b，则＝＋＝(＋)＝(＋)＝(＋－)＝(－a＋b＋c)，∵＝＋＝a＋b.∴·＝(－a＋b＋c)·(a＋b)＝(b2－a2＋c·a＋c·b)＝(|b|2－|a|2＋0＋0)＝0.∴⊥，即EF⊥AB1，同理，EF ⊥B.又AB 1∩B 1C ＝B 1，AB 1⊂平面B 1AC ，B 1C ⊂平面B 1AC ，∴EF ⊥平面B 1AC .反思与感悟 本类型题目用向量法证明的关键步骤是建立空间直角坐标系，用坐标表示向量或用基底表示向量，证法的核心是利用向量的数量积或数乘运算．跟踪训练2 如图所示，在正方体ABCD —A 1B 1C 1D 1中，O 为AC 与BD 的交点，G 为CC 1的中点．求证：A 1O ⊥平面GBD .证明 方法一 如图取D 为坐标原点，DA 、DC 、DD 1所在的直线分别为x 轴，y 轴，z 轴建立空间直角坐标系．设正方体棱长为2，则O (1,1,0)，A 1(2,0,2)，G (0,2,1)，B (2,2,0)，D (0,0,0)，∴OA 1→＝(1，－1,2)，OB →＝(1,1,0)，BG →＝(－2,0,1)，而OA 1→·OB →＝1－1＋0＝0，OA 1→·BG →＝－2＋0＋2＝0.∴OA 1→⊥OB →，OA 1→⊥BG →，即OA 1⊥OB ，OA 1⊥BG ，而OB ∩BG ＝B ，∴OA 1⊥平面GBD .方法二 同方法一建系后，设面GBD 的一个法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧ BG →·n ＝0，BD →·n ＝0，∴⎩⎪⎨⎪⎧ －2x ＋z ＝0，－2x －2y ＝0.令x ＝1得z ＝2，y ＝－1，∴平面GBD 的一个法向量为(1，－1,2)，显然A 1O →＝(－1,1，－2)＝－n ，∴A 1O →∥n ，∴A 1O ⊥平面GBD .题型三 证明面面垂直问题例3 如图，底面ABCD 是正方形，AS ⊥平面ABCD ，且AS ＝AB ，E 是SC 的中点．求证：平面BDE ⊥平面ABCD .证明 设AB ＝BC ＝CD ＝DA ＝AS ＝1，建立如图所示的空间直角坐标系A －xyz ，则B (1,0,0)，D (0,1,0)，A (0,0,0)，S (0,0,1)，E (12，12，12)，连结AC ，设AC 与BD 相交于点O ，连结OE ，则点O 的坐标为(12，12，0)． 因为AS →＝(0,0,1)，OE →＝(0,0，12)， 所以OE →＝12AS →，所以OE →∥AS →. 又因为AS ⊥平面ABCD ，所以OE ⊥平面ABCD ，又OE ⊂平面BDE ，所以平面BDE ⊥平面ABCD .反思与感悟 利用空间向量证明面面垂直通常可以有两个途径：一是利用两个平面垂直的判定定理将面面垂直问题转化为线面垂直进而转化为线线垂直；二是直接求解两个平面的法向量，证明两个法向量垂直，从而得到两个平面垂直．跟踪训练3 在三棱柱ABC －A 1B 1C 1中，AA 1⊥平面ABC ，AB ⊥BC ，AB ＝BC ＝2，AA 1＝1，E 为BB 1的中点，求证：平面AEC 1⊥平面AA 1C 1C .证明 由题意知直线AB ，BC ，B 1B 两两垂直，以点B 为原点，分别以BA ，BC ，BB 1所在直线为x ，y ，z 轴建立如图所示的空间直角坐标系，则A (2,0,0)，A 1(2,0,1)，C (0,2,0)，C 1(0,2,1)，E (0,0，12)， 故AA 1→＝(0,0,1)，AC →＝(－2,2,0)，AC 1→＝(－2,2,1)，AE →＝(－2,0，12)． 设平面AA 1C 1C 的法向量为n 1＝(x ，y ，z )，则⎩⎪⎨⎪⎧n 1·AA 1→＝0，n 1·AC →＝0，即⎩⎪⎨⎪⎧ z ＝0，－2x ＋2y ＝0. 令x ＝1，得y ＝1，故n ＝(1,1,0)．设平面AEC 1的法向量为n 2＝(a ，b ，c )，则⎩⎪⎨⎪⎧ n 2·AC 1→＝0，n 2·AE →＝0，即⎩⎪⎨⎪⎧ －2a ＋2b ＋c ＝0，－2a ＋12c ＝0.令c ＝4，得a ＝1，b ＝－1.故n 2＝(1，－1,4)．因为n 1·n 2＝1×1＋1×(－1)＋0×4＝0，所以n 1⊥n 2.所以平面AEC 1⊥平面AA 1C 1C .1．已知平面α的法向量为a ＝(1,2，－2)，平面β的法向量为b ＝(－2，－4，k )，若α⊥β，则k＝________.答案－5解析∵α⊥β，∴a⊥b，∴a·b＝－2－8－2k＝0，∴k＝－5.2．设直线l1，l2的方向向量分别为a＝(－2,2,1)，b＝(3，－2，m)，若l1⊥l2，则m＝________. 答案10解析∵l1⊥l2，∴a·b＝0，∴－2×3－2×2＋m＝0，∴m＝10.3．若平面α，β垂直，则下面可以作为这两个平面的法向量的是________．(填序号)①n1＝(1,2,1)，n2＝(－3,1,1)②n1＝(1,1,2)，n2＝(－2,1,1)③n1＝(1,1,1)，n2＝(－1,2,1)④n1＝(1,2,1)，n2＝(0，－2，－2)答案①解析∵1×(－3)＋2×1＋1×1＝0，∴n1·n2＝0，故填①.4．若直线l的方向向量为a＝(2,0,1)，平面α的法向量为n＝(－4,0，－2)，则直线l 与平面α的位置关系为________．答案l⊥α解析∵a＝(2,0,1)，n＝(－4,0，－2)，∴n＝－2a，∴a∥n，∴l⊥α.5．已知平面α和平面β的法向量分别为a＝(1,1,2)，b＝(x，－2,3)，且α⊥β，则x ＝________.答案－4解析∵α⊥β，∴a·b＝0，∴x－2＋2×3＝0，∴x＝－4.正确应用向量方法解决空间中的垂直关系(1)线线垂直设直线l1、l2的方向向量分别是a、b，则要证明l1⊥l2，只要证明a⊥b，即a·b＝0.(2)线面垂直①设直线l的方向向量是a，平面α的法向量是u，则要证l⊥α，只需证明a∥u.②根据线面垂直的判定定理，转化为直线与平面内的两条相交直线垂直．即：设a、b在平面α内(或与平面α平行)且a与b不共线，直线l的方向向量为c，则l⊥α⇔c⊥a且c⊥b⇔a·c＝b·c＝0.(3)面面垂直①根据面面垂直的判定定理转化为证相应的线面垂直、线线垂直．②证明两个平面的法向量互相垂直．此文档是由网络收集并进行重新排版整理.word可编辑版本！。

空间向量及其线性运算学习目的：1．理解空间向量的概念，掌握空间向量的加法、减法和数乘运算 2．用空间向量的运算意义和运算律解决立几问题. 学习重点：空间向量的加法、减法和数乘运算及运算律 学习难点：用向量解决立几问题 学习过程：一、复习引入： 1平面向量的概念(1)向量的基本要素：大小和方向(2)向量的表示：几何表示法AB u u r ,a ；坐标表示法),(y x j y i x a(3)向量的长度：即向量的大小，记作｜a｜(4)特殊的向量：零向量a ＝0单位向量0a 为单位向量(5)相等的向量：大小相等，方向相同1122(,)(,)x y x y 1212x x y y(6)平行向量(共线向量)：方向相同或相反的向量，称为平行向量记作a ∥b由于向量可以进行任意的平移(即自由向量)，平行向量总可以平移到同一直线上，故平行向量也称为共线向量 2向量的运算向量的加减法，数与向量的乘积，向量的数量（内积）及其各运算的坐标表示和性质运算类型 几何方法 坐标方法 运算性质向 量 的 加 法 1平行四边形法则 2三角形法则a b b a )()(c b a c b a AB BC AC u u r u u r u u u r向 量 的 减 法三角形法则)(b a b a BA AB OB OA AB u u r u u r u u r向 量 的 乘 法1a 是一个向量,满足:2>0时,a 与a 同向; <0时,a 与a 异向; =0时, a =0a a )()(a a a )(b a b a )(a ∥b a b 向 量 的 数 量 积b a •是一个数10 a 或0 b 时,b a •=020 a 且0 b 时,),cos(||||b a b a b a •a b b a • •)()()(b a b a b a • • •c b c a c b a • • • )(22||a a 2121||y x a ||||||b a b a •3重要定理、公式：（1）向量共线定理 （2）平面向量基本定理21,e e是同一平面内两个不共线的向量，那么，对于这个平面内任一向量，有且仅有一对实数12, ，使1122a e e rvv(3)两个向量平行的充要条件 a ∥b(4)两个向量垂直的充要条件 a ⊥b二、讲解新课：1.空间向量的概念：在空间，我们把具有大小和方向的量叫做向量注：⑴向量一般用有向线段表示同向等长的有向线段表示同一或相等的向量 ⑵空间的两个向量可用同一平面内的两条有向线段来表示 2．空间向量的运算(如图）OB OA AB a b v r u u r u u r u u r BA OA OB a b r r u u r u u r u u r ()OP a R ru u rC B A O b bbaa运算律：⑴加法交换律：a b b a ⑵加法结合律：)()(c b a c b a⑶数乘分配律：b a b a)(3.共线向量及共线向量定理:定义:如果表示空间向量的有向线段所在的直线互相平行或重合,那么这些向量叫做共线向量或平行向量.向量a 、b 平行,记做a //b.定理：空间任意两个向量a 、b （b ≠0 ），a //b的充要条件是 .三、例题：例1已知在三棱柱111C B A ABC 中，M 是1BB 的中点，化简下列各式， 并在图中标出化简得到的向量。