2章_热力学第二定律习题课

第二章热力学第二定律一. 选择题：1. 理想气体绝热向真空膨胀，则( )(A) △S = 0，W = 0 (B) △H = 0，△U = 0(C) △G = 0，△H = 0 (D) △U = 0，△G = 02. 熵变△S 是(1) 不可逆过程热温商之和(2) 可逆过程热温商之和(3) 与过程无关的状态函数(4) 与过程有关的状态函数以上正确的是（(A) 1，2 (B) 2,3 (C) 2 (D) 4 3. 对于孤立体系中发生的实际过程，下式中不正确的是：（）(A) W = 0 (B) Q = 0 (C) △S > 0(D) △H = 04. 理想气体经可逆与不可逆两种绝热过程（）(A) 可以从同一始态出发达到同一终态(B) 不可以达到同一终态(C) 不能断定(A)、(B) 中哪一种正确(D) 可以达到同一终态，视绝热膨胀还是绝热压缩而定5. P⊖、273.15K 水凝结为冰，可以判断体系的下列热力学量中何者一定为零？(A) △U (B) △H (C) △S (D) △G6. 在绝热恒容的反应器中，H2和Cl2化合成HCl，此过程中下列各状态函数的变化值哪个为零？( )(A) △r U m(B) △r H m(C) △r S m(D) △r G m7. 在绝热条件下，用大于气筒内的压力，迅速推动活塞压缩气体，此过程的熵变为：( ) (A) 大于零(B) 等于零(C) 小于零(D) 不能确定8. H2和O2在绝热钢瓶中生成水的过程：（）(A) △H = 0 (B) △U = 0 (C) △S = 0(D) △G = 09. 在270K,101.325kPa 下，1mol过冷水经等温等压过程凝结为同样条件下的冰，则体系及环境的熵变应为：( )(A) △S体系< 0 ，△S环境< 0 (B) △S体系< 0 ，△S 环境> 0 (C) △S体系> 0 ，△S环境< 0(D) △S体系> 0 ，△S环境> 010. 1mol 的单原子理想气体被装在带有活塞的气缸中，温度是300K，压力为1013250Pa。

第二章热力学第二定律习题一、填空题1. H2O（l）在80℃，101.325 kPa下蒸发，状态函数（U、S、H、A、G）改变值不为零的有。

2.常压下，过冷水凝结成同温度的冰，则∆S体0，∆S总0。

3.i.g.任一不可逆过程回到始态，其体系∆S体0，∆S环0。

4.热温商δQ/T经证明为状态函数，其积分值必与熵变相等。

5. 100℃，1.5p的水蒸气变成100℃，p的液体水，ΔS______ 0, ΔG ______ 0。

6. 选择―>‖、―<‖、―=‖理想气体经节流膨胀，△S _____ 0，△G _____ 0.二、选择题1.在等温等压下进行下列相变：H2O (s,-10℃, p) = H2O (l,-10℃, p)在未指明是可逆还是不可逆的情况下，考虑下列各式哪些是适用的? ( )(1) ⎰δQ/T= ΔfusS(2) Q= Δfus H(3) Δfus H/T= Δfus S(4) －Δfus G = 最大净功(A) (1)，(2)(B) (2)，(3)(C) (4)(D) (2)2.纯液体苯在其正常沸点等温汽化，则：( )(A) Δvap U=Δvap H，Δvap F=Δvap G，Δvap S> 0(B) Δvap U<Δvap H，Δvap F<Δvap G，Δvap S> 0(C) Δvap U>Δvap H，Δvap F>Δvap G，Δvap S< 0(D) Δvap U<Δvap H，Δvap F<Δvap G，Δvap S< 03. 1 mol液苯，在其标准沸点下蒸发，则（）保持不变：（A）内能(B) 蒸汽压(C) 焓(D) 熵（E）体积（F）汽化热（G）A （H）G 4．H2（g）和O2（g）在绝热密闭钢瓶中反应生成水为零者是（）（A）ΔU(B) ΔH (C) ΔS(D) ΔG5.克劳修斯－克拉贝龙方程只适用于（）(A) 水在25℃，1atm空气中蒸发(B) 水在其标准沸点下蒸发达平衡(C) 水在其冰点时的固液相平衡(D)水在三相点时平衡6.公式－ΔG＝W′适用于（）(A) 孤立体系中的可逆过程(B) 封闭体系等温等压下可逆过程 (C) 封闭体系恒温恒容过程(E) 以上过程 7.100℃，105Pa 的水蒸气变成100℃，5×104Pa 的水蒸气，该过程的ΔG 与ΔA 的关系是（ ） A.ΔG=ΔA=0 B.ΔG=ΔA<0 C.ΔG<ΔA D.ΔG>ΔA.8. 下列各式中，哪个是化学势（ ）A.jn p T i n U ,,⎪⎪⎭⎫⎝⎛∂∂ B.,,j i T P n A n ⎛⎫∂ ⎪∂⎝⎭ C.jnp T i n H ,,⎪⎪⎭⎫⎝⎛∂∂ D.,,j i T P n G n ⎛⎫∂ ⎪∂⎝⎭ 9. 在定温定压下，二组分混合形成理想溶液，下列哪个函数的变化值正确（ ）A.ΔS=0B.ΔV=0C.ΔG=0D.ΔA=0 10. 100℃，105Pa 的水蒸气变成100℃，5×104Pa 的水蒸气，该过程的ΔG 与ΔA 的关系是（ ） A.ΔG=ΔA=0 B.ΔG=ΔA<0 C.ΔG<ΔA D.ΔG>ΔA.11.从热力学四个基本方程可导出VU S ∂⎛⎫= ⎪∂⎝⎭（ ）（A ）T A V ∂⎛⎫⎪∂⎝⎭ （B ）P H S ∂⎛⎫ ⎪∂⎝⎭ （C ）S U V ∂⎛⎫ ⎪∂⎝⎭ （D ）PG T ∂⎛⎫⎪∂⎝⎭12. 工作在100℃和25℃的两个大热源间的卡诺热机，其效率为( ) (A)20%(B)25%(C)75%(D)100%13单原子理想气体的R )2/3(,v C m =，温度由Ｔ１变到Ｔ２时，等压过程体系的熵变P S ∆与等容过程熵变V S ∆之比是：( )（A ）１∶１ （B ）２∶１（C ）３∶５(D)５∶３14. 下面诸式中不能称为基尔霍夫公式的是 ( ) （A ）m p pmC TH ,∆=⎪⎭⎫⎝⎛∂∆∂ （B ）⎰∆+∆=∆21,12)()(T T m p m m dT C T H T H(C) ⎰∆+∆=∆21,12)()(T T m V m m dT C T U T U （D ）p pC T H =⎪⎭⎫⎝⎛∂∂15. 一隔板两端，左边装有25℃、1×P θ、0.2mol O 2，右边装有25℃、1×P θ、0.8mol O 2，均视为理想气体，当抽走隔板后，混合过程的ΔS 为A 、0.994J·k -1B 、0C 、4.16J·k -1D 、－4.16J·k -116. 非理想气体进行绝热自由膨胀时,下述答案中哪一个错误?( )(A) Q =0 (B) W =0 (C) ΔU =0 (D) ΔH =0三、计算题1. 某物质的固体及液体的蒸气压可分别用下式表示： lg(p /Pa) = 11.454 - 1864.8/(T /K) （固体） (1) lg(p /Pa) = 9.870 - 1453/(T /K) （液体） (2)试求其： (1) 摩尔升华焓 (2) 正常沸点 (3) 三相点的温度和压力(4) 三相点的摩尔熔化熵2. 将495.5 K,600 kPa 的 1 mol N 2绝热可逆膨胀到100 kPa ，试求该过程的Q ,W ,ΔU ,ΔH ,ΔF ,ΔG ,ΔS ,ΔS 隔离。

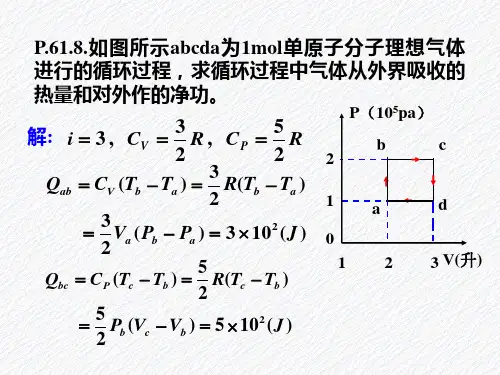
第二章-热力学第二定律第二章 热力学第二定律练习参考答案1. 1L 理想气体在3000K 时压力为1519.9 kPa ，经等温膨胀最后体积变到10 dm 3，计算该过程的W max 、ΔH 、ΔU 及ΔS 。

解: 理想气体等温过程。

ΔU =ΔH =0W max =⎰21V V p d V =⎰21V V VnRTd V =nRT ln(V 2/ V 1)=p 1V 1 ln(V 2/ V 1) = 1519.9×103×1×10-3×ln(10×10-3/ 1×10-3)=3499.7 (J ) =3.5 (k J ) 等温时的公式 ΔS =⎰21V V p d V / T =nR ln(V 2/ V 1) =W max /T=3.5×103/ 3000 =1.17 (J •K -1)2. 1mol H 2在27℃从体积为1 dm 3向真空膨胀至体积为10 dm 3，求体系的熵变。

若使该H 2在27℃从1 dm 3经恒温可逆膨胀至10 dm 3，其熵变又是多少？由此得到怎样结论？解: 等温过程。

向真空膨胀:ΔS = ⎰21V V p d V / T =nR ln(V 2/ V 1)(等温） =1×8.314×ln(10/ 1) = 19.14 (J •K -1)可逆膨胀: ΔS =⎰21V V p d V / T =nR ln(V 2/ V 1)=1×8.314×ln(10/ 1) = 19.14 (J •K -1)状态函数变化只与始、终态有关。

3. 0.5 dm 3 70℃水与0.1 dm 3 30℃水混合，求熵变。

解: 定p 、变T 过程。

设终态体系温度为t ℃，体系与环境间没有热传导；并设水的密度(1 g •cm -3)在此温度范围不变。

查附录1可得C p,m (H 2O, l ) = 75.48 J •K -1•mol -1。

《热力学第二定律》习题及答案选择题1．ΔG=0 的过程应满足的条件是(A) 等温等压且非体积功为零的可逆过程 (B) 等温等压且非体积功为零的过程 (C) 等温等容且非体积功为零的过程(D) 可逆绝热过程 答案：A2．在一定温度下，发生变化的孤立体系，其总熵（A ）不变 (B)可能增大或减小(C)总是减小(D)总是增大答案：D 。

因孤立系发生的变化必为自发过程，根据熵增原理其熵必增加。

3．对任一过程，与反应途径无关的是(A) 体系的内能变化 (B) 体系对外作的功 (C) 体系得到的功 (D) 体系吸收的热 答案：A 。

只有内能为状态函数与途径无关，仅取决于始态和终态。

4．下列各式哪个表示了偏摩尔量： (A),,j i T p n U n ⎛⎫∂ ⎪∂⎝⎭ (B) ,,j i T V n H n ⎛⎫∂ ⎪∂⎝⎭ (C) ,,j i T V n A n ⎛⎫∂ ⎪∂⎝⎭ (D) ,,ji i T p n n μ⎛⎫∂ ⎪∂⎝⎭ 答案：A 。

首先根据偏摩尔量的定义，偏导数的下标应为恒温、恒压、恒组成。

只有A和D 符合此条件。

但D 中的i μ不是容量函数，故只有A 是偏摩尔量。

5．氮气进行绝热可逆膨胀ΔＵ＝０ (B) ΔＳ＝０ (C) ΔA ＝０ (D) ΔＧ＝０答案：B 。

绝热系统的可逆过程熵变为零。

6．关于吉布斯函数G, 下面的说法中不正确的是(A)ΔG ≤W'在做非体积功的各种热力学过程中都成立(B)在等温等压且不做非体积功的条件下, 对于各种可能的变动, 系统在平衡态的吉氏函数最小(C)在等温等压且不做非体积功时, 吉氏函数增加的过程不可能发生(D)在等温等压下,一个系统的吉氏函数减少值大于非体积功的过程不可能发生。

答案：A 。

因只有在恒温恒压过程中ΔG ≤W'才成立。

7．关于热力学第二定律下列哪种说法是错误的(A)热不能自动从低温流向高温(B)不可能从单一热源吸热做功而无其它变化(C)第二类永动机是造不成的(D 热不可能全部转化为功答案：D 。

第二章热力学第二定律练习题答案一、判断题答案：1．对。

自然界发生的过程是以一定速率进行的，都是不可逆的，但不一定都是自发的，例如人们用电解水法制备氢气。

2．错。

例如，理想气体绝热不可逆压缩，就不是自发的。

3．错。

只有在孤立体系才成立。

非孤立体系不成立，例如电解水熵增加，但不自发的。

4．第1，2个结论正确，第3个结论错。

绝热不可逆压缩过程。

∆S > 0。

5．错。

系统由同一始态出发，经绝热可逆和绝热不可逆过程不可能到达相同的终态。

经绝热可逆，∆S = 0；绝热不可逆过程，∆S > 0。

6．错。

系统经循环过程后回到始态，状态函数都不改变，但不能依此来判断过程的性质，可逆循环与不循环都可以回到始态。

7．错。

正确说法是隔离系统平衡态的熵最大。

8．错。

正确的是绝热可逆过程中∆S = 0，绝热不可逆过程中∆S > 09．不矛盾。

理想气体经等温膨胀后，是的，吸的热全部转化为功，因气体的状态变化了，体积增大了，发生了其他变化。

10．错。

例如过冷水结冰，自发过程，但熵减少。

只有孤立体系或绝热体系，自发变化过程，∆S > 0。

11．错。

必须可逆相变才能用此公式。

12．错。

系统的熵除热熵外，还有构型熵。

例如NaOH固体溶于水，或C在氧气中燃烧，都是放热，但熵都是增加。

13．对。

固体、液体变成气体，熵是增加的。

14．错。

冰在0℃，pө下转变为液态水，不能认为是自发方程；同样在0℃，pө下液态水也可以变成冰，只能说是可逆过程（或平衡状态）。

15．错。

只有孤立体系才成立，非孤立体系不成立，例如过冷水结冰，ΔS< 0，混乱度减小，自发过程的方向就不是混乱度增加的方向。

16．错，必须在等温、等压的条件下才有此结论。

17．错。

若有非体积功存在，则可能进行，如电解水，吉布斯函数变化大于零。

18．错。

此说法的条件不完善，如在等温条件下，做的功（绝对值）才最多。

19．错。

基本方程对不可逆相变不适用。

20．错。

热力学第二定律课后习题答案习题1在300 K ，100 kPa 压力下，2 mol A 和2 mol B 的理想气体定温、定压混合后，再定容加热到600 K 。

求整个过程的∆S 为若干？已知C V ,m ,A = 1.5 R ，C V ,m ,B = 2.5 R[题解]⎪⎩⎪⎨⎧B(g)2mol A(g)2mol ，，纯态 3001001K kPa，（）−→−−−−混合态，，2mol A 2mol B100kPa 300K 1+==⎧⎨⎪⎪⎩⎪⎪p T 定容（）−→−−2混合态，，2mol A 2mol B 600K 2+=⎧⎨⎪⎩⎪T ∆S = ∆S 1 + ∆S 2，n = 2 mol∆S 1 = 2nR ln ( 2V / V ) = 2nR ln2 ∆S 2 = ( 1.5nR + 2.5nR ) ln （T 2 / T 1）= 4nR ln2 所以∆S = 6nR ln2= ( 6 ⨯ 2 mol ⨯ 8.314 J ·K -1·mol -1 ) ln2 = 69.15 J ·K -1 [导引]本题第一步为理想气体定温定压下的混合熵，相当于发生混合的气体分别在定温条件下的降压过程，第二步可视为两种理想气体分别进行定容降温过程，计算本题的关键是掌握理想气体各种变化过程熵变的计算公式。

习题22 mol 某理想气体，其定容摩尔热容C v ，m =1.5R ，由500 K ，405.2 kPa 的始态，依次经历下列过程：(1)恒外压202.6 kPa 下，绝热膨胀至平衡态； (2)再可逆绝热膨胀至101.3 kPa ； (3)最后定容加热至500 K 的终态。

试求整个过程的Q ，W ，∆U ，∆H 及∆S 。

[题解] （1）Q 1 = 0，∆U 1 = W 1， nC V ,m （T 2－T 1）)(1122su p nRT p nRT p --=， K400546.2022.405)(5.11221211212====-=-T T kPa p kPa p T p T p T T ，得，代入，（2）Q 2 = 0，T T p p 3223111535325=-=-=--()γγγγ，， T T 320.42303==-()K（3）∆V = 0，W 3 = 0，Q U nC T T V 3343232831450030314491==-=⨯⨯⨯-=∆,()[.(.)].m J kJp p T T 434350030310131671==⨯=(.).kPa kPa 整个过程：Q = Q 1 + Q 2+ Q 3 =4.91kJ ，∆U = 0，∆H = 0，Q + W = ∆U ，故W =－Q =－4.91 kJ∆S nR p p ==⨯=--ln (.ln ..).141128314405616711475J K J K ··[导引]本题的变化过程为单纯pVT 变化，其中U 、H 和S 是状态函数，而理想气体的U 和H 都只是温度的函数，始终态温度未变，故∆U = 0，∆H = 0。

第二章 热力学第二定律练习题一、判断题（说法正确否）：1．自然界发生的过程一定是不可逆过程。

2．不可逆过程一定是自发过程。

3．熵增加的过程一定是自发过程。

4．绝热可逆过程的∆S = 0，绝热不可逆膨胀过程的∆S > 0，绝热不可逆压缩过程的∆S < 0。

5．为了计算绝热不可逆过程的熵变，可以在始末态之间设计一条绝热可逆途径来计算。

6．由于系统经循环过程后回到始态，∆S = 0，所以一定是一个可逆循环过程。

7．平衡态熵最大。

8．在任意一可逆过程中∆S = 0，不可逆过程中∆S > 0。

9．理想气体经等温膨胀后，由于∆U = 0，所以吸的热全部转化为功，这与热力学第二定律矛盾吗?10．自发过程的熵变∆S > 0。

11．相变过程的熵变可由T H S ∆=∆计算。

12．当系统向环境传热时(Q < 0)，系统的熵一定减少。

13．一切物质蒸发时，摩尔熵都增大。

14．冰在0℃，pT H S ∆=∆>0，所以该过程为自发过程。

15．自发过程的方向就是系统混乱度增加的方向。

16．吉布斯函数减小的过程一定是自发过程。

17．在等温、等压下，吉布斯函数变化大于零的化学变化都不能进行。

18．系统由V 1膨胀到V 2，其中经过可逆途径时做的功最多。

19．过冷水结冰的过程是在恒温、恒压、不做其他功的条件下进行的，由基本方程可得∆G = 0。

20．理想气体等温自由膨胀时，对环境没有做功，所以 -p d V = 0，此过程温度不变，∆U = 0，代入热力学基本方程d U = T d S - p d V ，因而可得d S = 0，为恒熵过程。

21．是非题：⑴“某体系处于不同的状态，可以具有相同的熵值”，此话对否？ ⑵“体系状态变化了，所有的状态函数都要变化”，此话对否？ ⑶ 绝热可逆线与绝热不可逆线能否有两个交点？⑷ 自然界可否存在温度降低，熵值增加的过程？举一例。

⑸ 1mol 理想气体进行绝热自由膨胀，体积由V 1变到V 2，能否用公式：⎪⎪⎭⎫⎝⎛=∆12ln VV R S计算该过程的熵变？22．在100℃、p 时，1mol 水与100℃的大热源接触，使其向真空容器中蒸发成 100℃、p 的水蒸气，试计算此过程的∆S 、∆S (环)。

第二章热力学第二定律（习题）第二章热力学第二定律一、填空题1、可逆循环的热温商之和等于，在工作于温度为T1与T2两热源间的所有热机中，只有热机的效率最高，它的效率值可达η= 。

2、历史上曾提出过两类永动机。

第一类永动机指的是就能做功的机器。

因为它违反了定律，所在造不出来。

第二类永动机指的是，它并不违反定律，但它违反了定律，故也是造不出来的。

3、熵是系统的状态函数，按性质的分类，熵属于性质。

在隔离系统中，一切可能发生的宏观过程都是过程，均向着系统的熵值的方向进行。

直至平衡时，熵值达到此条件下的为止。

在隔离系统中绝不会发生熵值的过程。

4、从熵的物理意义上看，它是量度系统的函数。

当物质由它的固态变到液态，再变到气态时，它的熵值应是的。

而当温度降低时，物质的熵值应是的。

热力学第三定律的内容是。

5、下列各公式的适用条件分别是：对亥氏函数判据公式△A≤0，是。

对吉氏函数判据公式△G≤0，是。

对热力学基本方程式，如dG=-SdT+Vdp等，是。

6、热力学第一定律△U=Q+W的适用条件是；热力学第二定律△S≥0作判据时的适用条件是；热力学第三定律S（0K）=0的适用条件是。

7、理想气体的恒温过程为恒的过程；所有气体的节流膨胀为恒过程；所有系统的可逆绝热过程为恒；所有恒温恒压下的可逆相变过程为恒的过程。

8、理想气体从相同始态分别经绝热可逆膨胀和绝热不可逆膨胀到相同的终态压力，则终态的温度T可逆 T 不可逆，终态的体积V可逆 V不可逆（填入>、<或=）。

9、对于U、H、S、F和G等热力学量，（1）在绝热定容反应器中反应，过程中不变的量是。

（2）在373K和101325Pa下，液体水气化过程中不变的量是。

（3）气体绝热可逆膨胀过程中不变的量是。

（4）理想气体节流膨胀过程中不变的量是。

10、理想气体等温向真空膨胀，体积由V1变到V2，其△U ，△S 。

11、实际气体绝热自由膨胀，其△U 0，△S 0。

12、在、、的条件下，系统的自发变化总是朝着吉布期函数的方向进行的，直到系统达到平衡。

第二章 热力学第二定律一 热力学部分重点1 基本概念(1) 体系（封闭、敞开、孤立体系）与环境(2) 过程（可逆、等温、等压、等容、等外压、绝热、自由膨胀、节流膨胀） (3) 性质、平衡状态、状态函数（T, p, V , U, H, S, F, G ）、过程函数（热Q, 功W,Q V , Q p , 热容C ）2 几个定律(1) 热力学第一定律（文字+数学W Q U -=∆）(2) 热力学第二定律（文字+数学∑≥∆→BAB A TQS δ）(3) 热力学第三定律(4) Hess 定律 （状态函数“异途同归、变化相等”特性的必然结果） (5) Kirchhoff 定律（反应热与温度关系）dTC T H T H p T T r m r m r ⎰∆+∆=∆21)()(1o2o ；p r pr C T H ∆=⎪⎭⎫⎝⎛∂∆∂ (6) Gibbs-Helmhotz 公式（反应的自由能变化与温度关系）2)(T HT T Gp-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡∂∂，2)(TH TT G p∆-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∂∆∂，IdT TH TG +∆-=∆⎰2()p G G HS TT∂∆∆-∆=-∆=∂，00()()TT G T G T SdT ∆=∆-∆⎰若T 0为正常相变温度，0()0G T ∆=，0()T T G T SdT ∆=-∆⎰3热效应(1) 标准摩尔生成焓om f H ∆(2) 标准摩尔燃烧焓om c H ∆(3) ,,o o or m B f m B B c m B R P H H H ννεε∆=∆=-∆=-∑∑∑∑(4) Q p -Q V =∆r H-∆r U=∆nRT4 热力学重要公式(1) 定义式 H=U+pV ；F=U-TS ；G=H-TS ；dS=δQ R /T ；⎰=dVpW e热容 VV V TU dTQC )()(∂∂=≡δ；p p p TH dTQC )()(∂∂=≡δ焦-汤系数 11()()[()]J T H T p ppT H V V T pC pC Tμ-∂∂∂==-=--∂∂∂偏摩尔量 )(,,,)(B C C n p T Bm B n ZZ ≠∂∂=化学势)()()()(,,,,,,,,)()()()(B C C B C C B C C B C C n V T Bn p S Bn V S Bn p T BB n F n H n U n G ≠≠≠≠∂∂=∂∂=∂∂=∂∂=μ(2) i.g.状态方程 pV=nRT ，pV m =RTV an der Waals 方程 RT b V V a p m m=-+))((2(3) 绝热可逆过程方程 31211,,C TpC TV C pV ===--γγγγ(4) C p -C V 表达式])[()(p V UT V C C T p V p +∂∂∂∂=-（第一章） i.g. R C C m V m p =-,,p VVp TV Tp T C C )()(∂∂∂∂=- κα22)()(TV TV Vp T C C pT V p =∂∂∂∂-=-（κ=T pVV )(1∂∂-等温压缩系数，α=p T V V )(1∂∂等压膨胀系数） (5) 四个基本方程，Maxwell 关系式和T 、S 、p 、V 表达式B B dU TdS pdV dn μ=-+∑；p S S p V T ∂∂⎛⎫⎛⎫= ⎪ ⎪∂∂⎝⎭⎝⎭； pV S H S U T ⎪⎭⎫ ⎝⎛∂∂=⎪⎭⎫ ⎝⎛∂∂= B B dH TdS Vdp dn μ=++∑； V T T p V S ⎪⎭⎫⎝⎛∂∂=⎪⎭⎫ ⎝⎛∂∂； TS p Gp H V ⎪⎪⎭⎫⎝⎛∂∂=⎪⎪⎭⎫⎝⎛∂∂=B B dF SdT pdV dn μ=--+∑；S V S V p T ⎛⎫∂∂⎛⎫=- ⎪ ⎪∂∂⎝⎭⎝⎭； S T U F p V V ∂∂⎛⎫⎛⎫-== ⎪ ⎪∂∂⎝⎭⎝⎭ B B dG SdT Vdp dn μ=-++∑；p TT V p S ⎪⎭⎫⎝⎛∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂； p V G F S T T ∂∂⎛⎫⎛⎫-== ⎪ ⎪∂∂⎝⎭⎝⎭ (6) 热力学状态方程 pTp T VU V T -∂∂=∂∂)()(； VTV T pH p T +∂∂-=∂∂)()((7) 克劳修斯-克拉贝龙方程 VT H d Td p ∆∆= 克拉贝龙方程2ln RTH dTp d m vap ∆=（忽略液体体积，气体为i.g.）)11(ln2112T T RH p p mvap -∆=（m vap H ∆是常数）11m o lK J 88--⋅⋅≈∆bmvap T H （楚顿规则）(8) 规定熵 ⎰⎰⎰+∆++∆+=TT g p bvap T T l p fusfusT s p T bbfusfusT d C T H T d C T HT d C S ln ln ln ,,0,(9) 全微分性质()()()1Z x y x y z y zx∂∂∂=-∂∂∂ → ()()()Z y x x x z yzy∂∂∂=-∂∂∂ 循环关系1()()Z Zx y y x -∂∂=∂∂()()()()()()Z Z Z Z Z Z x x t x t k ytytky∂∂∂∂∂∂==∂∂∂∂∂∂传递关系2()()y x x y ZZ Z x y y x x y ⎡⎤⎡⎤∂∂∂∂∂==⎢⎥⎢⎥∂∂∂∂∂∂⎣⎦⎣⎦ Euler 倒易关系tx y t x y y Z x Z x Z ⎪⎭⎫⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫⎝⎛∂∂=⎪⎭⎫ ⎝⎛∂∂复合函数微分法 如 ()()()()p V T p U U U V TTVT∂∂∂∂=+∂∂∂∂)],(,[p T V T U U =→()()V T U U dU dT dVTV∂∂=+∂∂()()[()()]V T p T U U V V dT dT dp TVTp ∂∂∂∂=++∂∂∂∂dppV VU dT TV VU TU T T p T V )()(])()()[(∂∂∂∂+∂∂∂∂+∂∂=[()()()]()V T p T U U V U dT dp TVTp∂∂∂∂=++∂∂∂∂[,]U U T p = ()()p T U U dU dT dp Tp∂∂=+∂∂ 与上式比较即得5 自发过程的判断（封闭体系、W f =0）U 判据：∆U S,V ≤0 H 判据：∆H S,p ≤0S 判据：∆S 孤立=∆S 体系+∆S 环境 ≥0 F 判据：∆F T,V ≤0 G 判据：∆G T,p ≤0μ判据：S 和V ；S 和p ；T 和V ；T 和p 恒定的过程 0B B dn μ∑≤二 热力学部分的试题分析与解题思路热力学部分的题主要分三类：概念题、证明题、计算题1 概念题：如某公式的表达形式与适用范围；燃烧热、生成热、规定熵、反应热的定义与计算；某特定过程中状态函数与过程函数的特点；盖·吕萨克-焦耳实验；焦耳-汤姆逊节流过程等。