厦门市2016年初中生学业考试说明
- 格式:docx
- 大小:643.29 KB
- 文档页数:27

考生须知: 厦门市2007年初中毕业及高中阶段各类学校招生考试数学试题(试卷满分: 150 分; 考试时间:120分钟) 1. 解答的内容一律写在答题卡上, 考生不得擅自带走• 2. 作图或画辅助线要用 0.5毫米的黑色签字笔画好. 一、选择题(本大题共 7小题,每小题3分,共21分.每小题都有四个选项,其中有且只有 一个选项是正确的) 下列计算正确的是 A . — 3X 2 = — 6 B. — 1— 1 = 0 已知点 A (— 2, 3),则点A 在 A .第一象限 B .第二象限 下列语句正确的是 A.画直线AB = 10厘米 C.画射线OB = 3厘米 下列事件,是必然事件的是 A. 掷一枚均匀的普通正方体骰子,骰子停止后朝上的点数是B. 掷一枚均匀的普通正方体骰子,骰子停止后朝上的点数是偶数C. 打开电视,正在播广告 D •抛掷一枚硬币,掷得的结果不是正面就是反面 1.2. 3. 4.6. 7. 否则以0分计算.交卷时只交答题卡,本卷由考场处理, C. ( — 3)2= 6 C.第三象限D. 2 -1 = 2 D.第四象限B.画直线 D.延长线段AB 到点C,使得BC = AB I 的垂直平分线 方程组丿x + y = 5, 的解是,2x — y = 4.X= 3, x = 3, x =— 3, x =— 3, A .彳 B . C .丿D. \ly = 2. w=— 2.j= 2. 丁=— 2.5. 如果两个角是对顶角,那么这两个角相等;②如果一个等腰三角形下列两个命题:①有一个内角是60° ,那么这个等腰三角形一定是等边三角形 .则以下结论正确的是A.只有命题①正确B.只有命题②正确C.命题①、②都正确D.命题①、②都不正确小宝和爸爸、妈妈三人在操场上玩跷跷板,爸爸体重为 69千克,坐在跷跷板的一端,体重只有妈妈一半的小宝和妈妈一同坐在跷跷板的另一端,这时爸爸的一端仍然着地 .后来 小宝借来一副质量为 6千克的哑铃,加在他和妈妈坐的一端,结果爸爸被跷起离地 .小宝的体重可能是 A. 23.2 千克B. 23千克C. 21.1 千克D. 19.9 千克二、填空题(本大题共 10小题,每小题4分,共40分) 9.已知/ A = 50°,则/ A 的补角是 计算15 车序号1 2 3 4 5 6 车速(千米/时) 85 100 90 82 70 82 不等式2x — 4> 0的解集是 ________ . _______ 一名警察在高速公路上随机观察了 6辆车的车速,如下表所示: 则这6辆车车速的众数是 _______________ 千米/时. 已知图1所示的图形是由6个大小一样的正方形拼接而成的,此图形能否折成正方体 _________ (在横线上填“能”或“否”). 已知摄氏温度(C )与华氏温度「F )之间的转换关系是: 5摄氏温度=9 % (华氏温度—32).若华氏温度是68 F, 则摄氏温度是 C . 已知在 Rt △ ABC 中,/ C = 90°,直角边 AC 是直角边 BC 的2倍,贝U sin / A 的值 是 如图2,在平行四边形 ABCD 中,AF 交DC 于E ,交BC 的延长线于F ,若/ DAE = 20° , / AED = 90°,则/ B = __________ 度;若E C = 1,AD = 4厘米,则CF = _____________ 厘米. AB 3 在平面直角坐标系中, O 是坐标原点•点P (m , n )在反 图2 、 k 厂 比例函数y = X 的图象上.若m = k , n = k — 2,则k = ____________ ;若m + n = ,2k, OP = 2, k 且此反比例函数 y = -满足:当x > 0时,y 随x 的增大而减小,则 k =—— X 解答题(本大题共 9小题,共89分) 2 “ 2 ——1 V + X (本题满分8分)计算X 一 十J 厂+ 1. x x (本题满分8分)一次抽奖活动设置了如下的翻奖牌,如果你只能有一次机会在 字中选中一个翻牌,(1)求得到一架显微镜的概率;9个数(2)请你根据题意写出一个事件,使这个事件发生的概率是2 9.10. 11. 12. 13. 14.15. 16. 17. 三、 18. 19.1 2 3 4 5 6 789翻奖牌正面一架 两张 谢谢显微镜球票 参与 一张 一副 一张 唱片 球拍 唱片 两张 一张 一副 球票唱片球拍翻奖牌反面(本题满分8分)已知:如图3, AB 是O O 的弦,点(1) 若/ OAB = 35°,求/ AOB 的度数; (2) 过点C 作CD // AB ,若CD 是O O 的切线,求证:点C 是AB 的中点.21. (本题满分9分)某种爆竹点燃后,其上升的高度h (米)和时间t (秒)符合关系式1h = v o t — 2g t 2 ( O v t W 2),其中重力加速度 g 以10米/秒2计算.这种爆竹点燃后以 V o = 20 米/秒的初速度上升, (1) 这种爆竹在地面上点燃后,经过多少时间离地15米?(2) 在爆竹点燃后的1.5秒至1.8秒这段时间内,判断爆竹是上升,或是下降,并说明 理由. 22. (本题满分10分)已知四边形ABCD ,对角线AC 、BD 交于点O.现给出四个条件:①AC 丄BD :②AC 平分对角线 BD :③ AD // BC :④ / OAD = Z ODA.请你以其中的三个 条件作为命题的题设,以“四边形 ABCD 是菱形”作为命题的结论,(1 )写出一个真命题,并证明;(2 )写出一个假命题,并举出一个反例说明.23. (本题满分10分)已知:如图4,在厶ABC 中,D 是AB 边上的一点,BD > AD ,/ A =Z ACD ,(1)若/ A =Z B = 30 °,BD =3,求 CB 的长;(2 )过D 作/ CDB 的平分线 DF 交CB 于F ,C若线段AC 沿着AB 方向平移,当点 A 移到点D 时,F判断线段AC 的中点E 能否移到线段 DF 上,并说明理由. ______________________________ADB20. 图3图424. (本题满分12分)已知抛物线的函数关系式:y= x2 3+ 2( a —1) x+ a2-2a (其中x是自变量),(1)若点P(2,3)在此抛物线上,①求a的值;②若a> 0,且一次函数y= kx+ b的图象与此抛物线没有交点,请你写出一个符合条件的一次函数关系式(只需写一个,不必写出过程) ;(2)设此抛物线与x轴交于点A (x1, 0)、B (x2, 0).若xi^^3< x2,且抛物线的顶点3在直线x= 4的右侧,求a的取值范围.25. (本题满分12分)已知:如图5, PA、PB是O O的切线,A、B是切点,连结OA、OB、OP,(1)若/ AOP = 60°,求/ OPB 的度数;A(2 )过O作OC、OD分别交AP、BP于C、D两点,判断直线CD与O O的位置关系,并说明理由①若/ COP = Z DOP,求证:AC = BD;②连结CD,设△ PCD的周长为I,若I = 2AP,图526. (本题满分12分)已知点P (m, n) ( m>0)在直线y= x+ b (0< b< 3)上,点A、B4 2 2在x轴上(点A在点B的左边),线段AB的长度为3匕,设厶FAB的面积为S,且S=?b 2+ 3b,3(1 )若b = 2,求S的值;(2 )若S= 4,求n的值;(3)若直线y= x + b ( 0< b< 3)与y轴交于点C,A PAB是等腰三角形,当CA // PB时,求b的值.厦门市2007年初中毕业及高中阶段各类学校招生考试数学参考答案及评分标准题号 1 2 3 4 5 6 7 选项A BDD AC C、选择题(本大题共 7小题,每小题3分,共21分)二、填空题(本大题共 8. 3. 9. 130 度. 10小题,每小题4分,共40 分)10.5.11. x >2.12.82千米/时.13. 台匕 冃匕.14. 20 C .15.5 16. 70 度2厘米.17.3; 2.三、解答题(本大题共 (本题满分8分) 2 , 2 解:匸1X + X x 9小题,共89分) 18. 2 2x — 1 x • ~~2~7~■x x + x 19. (本题满分 (1)解:8分) ]9.20. (x — 1)( x + 1) x — 1 + 1=x.x(x + 1) + 1解:••• 0A = OB ,” 1 分 •• / OAB = Z OBA . ” 2 分 • • / OAB = 35° , ” 3 分 •• / AOB = 110°. ”4 分(2)证明:连结0C ,交AB 于E .(1) 如得到“一副球拍”或得到“两张球票”或 “一架显微镜或谢谢参与” . (2)解:得到 (本题满分8分)CD 是O 0的切线, ••• 0C 丄 CD .CD // AB , • / OEB = Z OCD . • 0E 丄AB . •/ 0A = OB ,• △ AOB 是等腰三角形,OE 是等腰三角形 AOB 顶角的平分线.•••点C 是AB 的中点.21.(本题满分9分)(1)解:由已知得,15 = 20t — |x 10X t 2,整理得,t 2 — 4t + 3= 0.解得,h= 3, t 2= 1当t =3时,不合题意,舍去• •当爆竹点燃后1秒离地15米.2(2)解:由题意得, h =- 5t + 20t.20•顶点的横坐标t =-莎)=2.2或:h =— 5( t — 2) + 20•顶点的横坐标t = 2.又••• 一 5V 0,二抛物线开口向下.•在爆竹点燃后的1.5秒至1.8秒这段时间内,爆竹在上升•22.(本题满分10 分)(1)真命题:如图,已知四边形ABCD ,对角线AC 、BD 交于点O.若平分对角线BD , AD // BC ,则四边形ABCD 是菱形.证明:•/ AD // BC ,• / CBO =Z ADO .•/ AC 垂直平分 BD , • Rt △ AOD 也 Rt △ COB . • AD = BC .•四边形ABCD 是平行四边形.(2)假命题1:已知四边形ABCD ,对角线AC 、BD 交于点O.若AC 丄BD , AC 平分对 角线BD ,/ OAD = Z ODA ,则四边形 ABCD 是菱形. 反作等腰直角三角形 ABD ,/ A = 90°,以BD 为一边,作等边三角形 BCD ,连结AC 、BD 交于点O. 贝U AC 丄BD , AC 平分对角线 BD ,/ OAD = Z ODA”9分•/ AC 丄 BD , 四边形ABCD 是菱形.AC 丄 BD , ACD3分但四边形ABCD不是菱形. ,,10分假命题2 :已知四边形ABCD,对角线AC、BD交于点O.若AC丄BD, AD // BC, / OAD = Z ODA,则四边形ABCD是菱形. ”6分反例:作等腰直角三角形AOD,/ AOD = 90° .延长DO至B, AO至C,取OB = OC (OB M OD ).连结AB、BC、CD ,贝U AC 丄BD , AD // BC,/ OAD = Z ODA. ,, 9 分则四边形ABCD是等腰梯形,不是菱形•,,10分假命题3:已知四边形ABCD,对角线AC、BD交于点O.若AC平分对角线BD , AD // BC,/ OAD = / ODA,则四边形ABCD是菱形. ”6分反例:作等腰三角形AOD ( OA = OD,/ AOD丰90°).延长DO至B,AO至C,取OB= OC= OA = OD.连结AB、BC、CD,贝U AD 丰 AB,AC 平分对角线BD,AD // BC,/ OAD = / ODA. ,,9分则四边形ABCD是矩形,不是菱形.5510分23.(本题满分10分)(1)解:•/ /A =/ ACD = 30°,CF ••• / CDB = 60° . ,, 1 分E又T/ B = 30°,A D B• / DCB = 90° . ,, 2 分亠亠BC在Rt△ BDC 中,cosB = BD,553分厂血3BC —BD •cosB — 3 •—.v2 2554分(2)解: •/ / CDB — / A +/ ACD,且DF 是/ CDB 的平分线,• 2 / FDB —2/ A,• / FDB —/ A. •AC // DF.5分方法 1 T / FDB =/ A,/ B =/ B,△ BDF s\ BAC.DF = BDAC = BA.BD > AD, DF 1> —AC 2BD、1 -- 〉_BA 2•/ E是AC的中点,•AE >1.即DF > AE.点E可以移到线段DF上.10分方法2:记点M为线段AB的中点,T BD >AD,点M在线段BD上.过M作MN // AC交BC于N./ BMN = / A,Z B =Z B,△ BMN BAC.BN = BM = 1BC = BA = 2N是BC的中点.MN // AC, AC// DF MN // DF.点N在线段BF上.点M在线段BD上,••• MN v DF.••• M为AB的中点,N是BC的中点,AE v DF.•••点E可以移到线段DF上.方法3:记点M为线段AB的中点,T BD > AD,”8分MN = AE.”9分”10分点M在线段BD上.过M作MN // AC交BC于N. / BMN = / A,Z B =Z B,△BMN BAC.MN = BM = 1AC = BA = 2.1E 为 AC 的中点,••• MN = 2AC = AE.MN // AC , AC // DF , 点M 在线段BD 上, MN BM 彳DF BD MN v DF. AE v DF.点E 可以移到线段DF 上.方法4:如图,延长 DF 至G ,使得DG = AC.•四边形ADGC 是平行四边形. • CG // AB.•••/ CGF =Z FDB ,/ GCF = Z FBD .△ CFG BFD. GF = CG FD = DB . CG = AD , AD v DB.即 計• GF + FD v 2F D. • DG > 2.1 FD > 2AC.又••• E 是AC 的中点,24.(本题满分12分)(1 [① 解:由题意得,3=4 + 2( a — 1) X 2 + a — 2a,”1 分 整理得,a 2+ 2a — 3= 0. ”2 分 解得,a 1=— 3, a 2= 1.”4 分9 / 12MN // DF.9分 10分CG DB v 1.• FD > AE.点E 可以移到线段DF 上. 9分 10分②解:y = x — 2.、.22(2)由题意得,x + 2( a — 1) x + a — 2a = 0解得,X 1 = — a , X 2 = — a + 2.解得一-,/3 v a v 2 — /3.3 1• 3 — a >4,解得 a v 4.3 I I1 8• S^- • AB • n , • -x- • n = 4.X 1< 3 v X 2,—a v” :3 v — a + 2.可以解得顶点坐标为(1 — a , — 1).11分10分△ OCP ^A ODP.CP = DP.•/ FA 、PB 是O O 的切线, • FA = PB. .AC = BD.② 证明 1:连结 CD.•/ l = 2AP , PA = PB ,CD = AC + BD.•/ OA = OB ,且/ OAC = Z OBD = 90° .•/ OC 1 = OC , DC 1= DC , OD = OD , ••• △ OCDOCD.10 / 1225. 12分(本题满分12分)(2)① 证明:•••/ COP =Z DOP ,/ CPO = Z DPO , PO = PO ,(1).将厶OAC 绕点O 逆时针旋转,使点 A 与B 重合. 记点C 的对称点为 C 1,. AC = BC 1,OC = OC 1.vZ OAC =Z OBD = 90°,•••点 C 1在PB 的延长线上.过O 作OE 丄CD , E 是垂足.即0E 是点0到直线CD 的距离, 112 X CD® 2 X CD &0B = OE.直线CD 与O O 相切.证明 2:过 O 作 OE 丄CD.设 OE = d , CE = x, DE = y.2 A —2 , A —22_122 , . -.22d = AC + AO — x , d = BD + AO — y ,••• AC 1 4— BD 2+ y 2— x 2= 0”8 分••• ( AC + x)( AC — x) = (BD + y)( BD — y)l = 2AP , FA = PB , • x + y = AC + BD.”9 分AC — x = y — BD.• ( AC + x)( y — BD) = (BD + y)( BD — y). (y — BD) (AC + x + BD + y )= 0.• ( AC + x + BD + y )M 0, - -y — BD = 0.BD = y.• d = AO. •直线CD 与O O 相切.26.(本题满分12分)32 9 23 (1)解:• b = -,• S = x + x-23 4 3 2=5 =2.” 2 2 2 (2)解:• S = 4,• 4 = 3b + 3b.• b 2 + b — 6 = 0. 解得 b =— 3 (舍去),b = 2.• AB 的长度为3.4 1 1 ,2 3n = 3.2 2 1⑶解:• S = 3b 2 + 3b , S = 2 •丨 AB| • n ,11分 12分10分11分 12分1分2分 3分4分5分 6分31 42 2 2 2 • §b • n = 3b + 3b. ■/ b z 0,n = b + 1. /• m + b = b + 1./• m = 1.P (1, b +1)过P 作PD 垂直x 轴于点D ,则点D (1 , 0). 4 1PD — AB = b + 1 — 3b = 1 — 3b. ” 8 分 1■/ 0 v b v 3,二 1 — §b > 0.”9 分••• PD > AB. •/ PA > PD , PD >AB ,「. PA > PD > AB ,即 PA >AB. •••PA 工 AB.同理 PB z AB”10 分2 2••• △ PAB 是等腰三角形,• PA = PB. • A (1— 3b , 0), B (1+ -b , 0)方法 1:v CA // PB ,••• / OAC =Z DPB ,• Rt △ AOC s Rt △ BDP.23• 4b — b — 3 = 0. •- b = 1 或 b = — 4 (不合题意,舍去)b = 1.方法2:延长PA 交y 轴于点C 1,v PA = PB ,/ CAO = Z PBA =Z PAB =Z OAC 1• OC 1= OC ,• C 1 (0, — b ).设直线 PA 的解析式为:y = kx +1. "k + t = b + 1, "k = 2b + 1, 则有* 解得,’L. t =— b. L_t =— b.•直线PA 的解析式为:y = (2 b + 1)x — b.” 11分/ 2 2--0 = (2 b +1) (1 — 3b )— b.•- 4 b — b — 3 = 0.3CO = OA PD = DB1 — 3b11分3b12分Rt △ AOC 也 Rt △ AOC .•- b= 1或b=—4 (不合题意,舍去).•b= 1. ”12分。

2016年厦门市中考英语试卷解析(二)基础知识与运用(每小题1.5分,共30分)V. 选择填空:从A、B、C中,选出一个最佳答案完成句子。
17. -The milk shake tastes good. How do you make it?-It’s easy, just follow the_____.A.discussionsB. instructionsC. resolutions18. -What a great thing to have a robot at home!-Robots are really useful. One day they will help people do almost_____.A. somethingB. everythingC. nothing19. -Have you seen the movie Zootopia?-Yes, I’ve seen it twice. Of all the movies I’ve ever seen, it’s the ______one.A.interestingB. more interestingC. most interesting20.-I think everyone should play a part in saving our environment.-I agree. For example, there will be less air pollution _____we drive less.A.ifB. soC. though21.-These shoes look cool. _____are they?-They are on sale, only $69.A.How muchB. How longC. How many22.-Tom, let’s hang out after school.-Sorry. I have ____Frank to work on the biology report with him.A. advisedB. expectedC. promised23. -It’s the second time I came to Xiamen. It _____a lot.-Yes, it’ s more and more beautiful.A.was changingB. has changedC. will change24. -These days, teenagers often have to do what they _____to.-It’s not good for their independence. They need to think on their own.A. tellB. are tellingC. are told25. -I’ve made much progress in grammar. The ideas you _____worked out fine.-Glad I could help.A. came up withB.ran out ofC. looked up to26. -I’d like to read some Chinese classics. Any suggestions?-Journey to the West. It’s a book ____is about Monkey King.A.whatB. whoC. that27.-Does anybody want to share ______on Father’s Day?-I bought a tie for my father. He loves it.A.what you didB. where you wentC. when you stopped28. -Would you like to go to Shanghai Disneyland? It opened this June.-______. I’m sure I’ll have a great time there.A.I’m afraid notB. It doesn’t matterC. That sounds like fun【答案解析】17. B 考查名词词义辨析。

厦门市云顶学校2021-2021学年〔上〕七年级期中考试地理试卷〔试卷总分值:100分考试时间:60分钟〕总分:一、选择题〔每题只有一个正确答案,将正确答案的字母填在表中。
每题2分共50分〕1.某地区民居墙体厚实,屋内建有火坑,窗户比拟小,有的窗户还装上了双层玻璃,屋顶高耸.这种民居的建筑风格反映该地区〔〕A.【答案】A【解析】试题分析:此题考查气候对民居的影响。
据题干信息可知,某地区民居“墙体厚实,屋内建有火坑,窗户比拟小,有的窗户还装上了双层玻璃〞起到防寒保暖的作用,屋顶高耸,可以减少雪的堆积,故其反映了气候寒冷的特点。
考点:气候对生产、生活的影响2.以下图中,A点在B点的什么方向〔〕A.东南方 B.西北方 C.东北方 D.西南方【答案】B【解析】试题分析:此题考查地图上的方向的判断。
图上可知,没有任何方向标志,故把B点的根本方向,可以判断A点位于B点的西北方向。
应选:B。
考点:地图上的方向3. 如果在地图上量得两地间的距离为3厘米,图上比例尺为1:10 000 000,算得两地间实地距离大约是〔〕A.300千米 B.3000千米 C.30千米 D.3千米【答案】A【解析】试题分析:根据比例尺=图上距离/实地距离,得:实地距离=图上距离÷比例尺=3厘米÷10000000=30000000厘米=300千米。
应选:A。
4.以下四幅地图,图幅大小相同,那么比例尺最大的是〔〕【答案】D【解析】试题分析:此题考查比例尺大小与范围大小之间的关系。
在图幅相同的情况下,比例尺越大,表示的范围越小,厦门市的范围最小,故其比例尺最大。
考点:地图5.当你到一个陌生的城市旅游时,你应选择〔〕【答案】D【解析】试题分析:此题考查地图的选择。
到一个陌生的城市旅游,需要了解该地的旅游景点和交通状况,故应该选择城市旅游交通地图。
考点:地图6.以下图例表示铁路的是〔〕A. B. C. D.【答案】A【解析】试题分析:此题考查常用的图例。

厦门中考总分是多少
初中学业水平考试,简称“中考”,是检验初中在校生是否达到初中学业水平的考试;它是初中毕业证书发放的必要条件,考试科目将国家课程方案所规定的学科全部列入初中学业水平考试的.范围。
接下来由小编为大家整理出厦门中考总分是多少,希望大家喜欢!
考试成绩计算
各科目卷面满分值如下:
1、语文150分、数学150分、英语150分。
2、物理100分。
3、化学100分。
4、道德与法治100分。
5、历史100分。
6、地理100分。
7、生物100分。
8、体育满分值30分。
9、物理实验、化学实验和生物实验(以下简称“实验”),以及信息技术考试的成绩分为合格或不合格。
升学成绩计算
考生的升学投档分由以下六部分组成:
(1)语文、数学、英语的卷面成绩100%;
(2)物理卷面成绩的90%;
(3)化学卷面成绩的60%;
(4)道德与法治卷面成绩的25%;
(5)体育分值;
(6)照顾分。
投档分四舍五入,总分值为655分加照顾分。
2020年,初二年学生的地理和生物明年以30%(满分100分)计入中考总分。
往年地理和生物只算等级,不算分。
附:考试科目等级计算
语文、数学、英语、物理、化学、道德与法治、历史、地理、生物等九个学科(以下简称“九科”)实行考试等级制度。
按卷面成绩依考生总数的4:3:2:1的比例分别折合为A、B、C、D四个等级。

2016年福建省厦门市中考语文试卷及答案(试卷满分:150分考题时间:120分钟)第一部分积累与运用(满分:37分)一、语言积累(13分)1、根据提示填写古诗文。
(13分)(1)长风破浪会有时,。
(李白《行路难》)(1分)(2)黑云压城城欲摧,。
(李贺《雁门太守行》)(1分)(3),似曾相识燕归来。
小园香径独徘徊(晏殊《浣溪沙》)(1分)(4)何处望神州?,千古兴亡多少事?悠悠。
(辛弃疾《南乡子》)(2分)(5)虽有嘉肴,弗食,;虽有至道,弗学,。
(《礼记·学记》)(6)醉翁之意不在酒,。
山水之乐,。
(欧阳修《醉翁亭记》)(2分)(7)白居易在《钱塘湖春行》中用鸟儿争春描绘初春景象的句子是“,。
(2分)(8)《爱莲说》中用来形容不与世俗同流合污而又洁身自好的君子之风的句子是“,”。
(2分)二、语言运用(23分)2、根据情境,将下列对话补充完整。
(4分)除夕一早,小新见邻居王阿姨对着一副春联发呆,便热心上前询问:“(1)?”王阿姨说:“哎!我分不清上下联,怎么办?”小新看了看那副春联(如图所示),指着它的末字,笑着解释道:“(2)。
”【提示:上联的末字是仄声(三声、四声),下联的末字是平身(一声、二声)】答:3、阅读下面的语段,完成(1)—(3)题。
(8分)我何其幸运,可以看到美的事物,看到一朵野姜花在湿润的空气里慢慢绽放,看到天空中行走散步的云变幻多姿。
我何其幸运,可以听到美的声音,听到鸟雀啼鸣低回宛转,听到蛙虫喧叫的热闹欢喜。
我何其幸运,。
生命是不会有真正的黑暗的。
(1)请将语段中的词语“何其幸运”,用正楷字工整地抄写在“田”字格内。
(3分)(2)以下四组词语字音字形都正确...的一项是()(2分)A、变幻多姿zhī低回宛wǎng转B、花团锦簇cù义愤填膺yīngC、风尘苦旅lǔ幽yoū游自在D、根生蒂dì固麟次栉chì比(3)仿照以上语段中的划线句,将句子补充完整。

附件22016年厦门市中招体育考试项目测试细则(修订版)一、中跑:800米(女)、1000米(男)1.场地器材(1)采用电子仪器计时。
(2)拥有周长400米、道次不少于6个的标准塑胶田径场,道宽1.22米至1.25米,800米及1000米起点、终点以及各分道有明确标志。
2.测试方法(1)进入测试区,考生出示准考证,经检录裁判核实身份并领取带号码的中跑背心,将背心套在身上后将准考证交检录裁判,检录裁判在考生准考证上注明对应的号码,按20人左右一组完成检录后将考生准考证交成绩记录裁判,并将考生带至起点处;起点裁判交代注意事项并引导考生进入起跑线,采用站立式起跑。
(2)当考生听到主裁判发出“各就位→跑”的指令起跑,计时器随起跑声开始计时;考生到达终点线时,由主裁判唱报考生最终的成绩分值;终点裁判唱报考生号码,直至最后一名考生在有效时间内到达终点;同时两名成绩记录裁判分别在成绩记录单上根据主裁判及终点裁判唱报的结果做好成绩记录,核对无误后在考生准考证上的对应成绩栏上盖章确认。
(3)测试过程中,技术裁判负责做好考生跑步脱圈的记录,并对考生的犯规及时提醒。
如遇考生途中摔倒、或途中受阻等影响考生正常发挥跑速的情况,项目主裁判可根据实际情况决定考生是否进行重测或建议考生办理缓考。
3.注意事项(1)测试过程,考生不得穿钉鞋、皮鞋、塑料凉鞋;开跑时注意听口令起跑。
(2)每组起跑时,若有考生被判犯规抢跑,应立即召回本组所有考生重跑。
(3)在弯道跑过程中,考生不得踩踏第一跑道的内侧分道线,否则将被判为犯规。
(4)考生犯规累计不得超过两次。
(5)考生参加本项目测试后,须在考点指定位置领取准考证。
二、100米游泳(泳姿不限)1.场地器材(1)采用人工计时(或电子仪器计时)。
(2)拥有泳池长50米、宽不少于15米的游泳池;道宽至少2.5米,100米游泳起点、终点以及各分道有明确标志。
2.测试方法(1)进入测试区,考生出示准考证,经检录裁判核实身份并安排道次后带入起点处;起点裁判交代注意事项并引导考生进入游泳起点处(进入水中),一手触及池壁。

附件12016年初中学业水平考试安排附件22016年市内三区普通高中报名要求一、网上志愿填报(一)报名时间。
5月19日(星期四)8:00-5月21日(星期六)20:00(二)网上志愿填报网址。
青岛市初中学业水平考试(高中阶段学校招生)管理平台(/)(三)有关要求。
1.考生须在规定的时间内登陆报名网址进行报名。
2.考生网上报名需选择自己的报考志愿(含是否服从分配)、填写监护人的有关信息和考生的其他信息。
其中考生第一志愿、监护人有关信息、联系电话、家庭住址、邮政编码等信息为必填内容。
3.考生报名信息填报完成并确认提交后,应同时打印《青岛市初中学业水平考试(高中阶段学校招生)网上报名信息表》。
普通高中志愿填报后不能再修改。
4.网上报名结束后,考生须在规定时间内,持相关材料到第一志愿普通高中学校现场确认报名。
届时,学生加分优待项目信息由第一志愿学校录入。
5.考生如对网上报名系统信息有异议(不含普通高中志愿信息),可在现场确认时提出,由第一志愿学校受理。
二、现场确认(一)普通高中现场确认报名地点及时间。
1.地点:第一志愿普通高中学校。
2.时间:5月22日(星期日)上午8:00至下午6:00。
5月23日(星期一)补充现场确认(二)现场确认报名需携带的证件和材料。
1.《青岛市初中学业水平考试(高中阶段学校招生)网上报名信息表》一份(通过网上报名系统打印);2.综合素质发展评价档案(含《综合素质发展评价表》、《中学生综合素质发展评价手册》、学生成长的标志性成果、至少一份研究性学习报告等)。
其中,标志性成果包括市级及以上教育部门组织或参与组织的各类比赛、评优获奖证书原件及复印件、能够反映个人成长的其他成果资料等;3.享受加分优待政策有关证件原件及复印件。
以上各种证件的原件,由第一志愿学校查验后返还考生,证件复印件及其他报名材料由报名学校保存在考生的报名档案袋中。
(三)普通高中学校通过“青岛市初中学业水平考试(高中阶段学校招生)管理平台”组织现场确认,考生报名信息填报完毕后,打印两份报名信息表,一份经学生或家长签字确认后粘贴到普通高中招生报名档案袋上,一份交由学生或家长留存。

厦门近十年中考作文真题 每次语文考试 ,大家最关心的就是作文 题了,下面是小编整理的厦门近十年中考作文真题,欢迎阅读。
2016 年福建厦门中考作文题 题目:那些年,_______相伴/遨游 2015 厦门中考作文题 二选一 一,“品”字从造字来说,由三个“口”组成,便是 告诉人们,品尝、品味 ...... 品尝美食是一种享受,品评事态是一种情怀 ……以“品”为话题,自拟题目,写一篇文章。
二,我的世界____。
加适当的词或词语,补足题目。
要求:1、文体不限。
2、不少于 500 字。
3、文中不能出现真实的人名、校 名、地名。
厦门 2014 年中考作文题 一,岸是水的边界,是限制,也是规则;它象征着归宿,承载着游子的思念 与寄托;饱含憧憬,写满孩童的梦想与期待;它既是起点,又是终点 ……请以“岸”为话题,自拟题目,写一篇文章。
二,____距离,加适当的词或词语,补足题目。
要求:1、文体不限,诗歌 除外。
2、不少于 500 字。
3、文中不能出现真实的人名、校名、地名。
厦门 2013 年中考作文题 二选一: 1 阳光、土地、空气的温度是人类生命之泉的本源,情感、文字、声音是人 类灵魂家园的归依,请以《温度》为话题写一篇文章; 2《在你身边,我____》(加上适当词语或短词,补足题目。
要求:扣题作文,不少于 500 字。
厦门 2012 年中考作文题 1.今天,新的奇迹出现在生命里;今天,智慧之声响彻校园;今天,爱在无偿 地传递;今天, 有人终于找到了自己的信仰;今天, 这世界因为我们的笑容被装点 得更美丽......今天 ,不是昨天一成不变的延续, 而是明天追逐梦想的开始。

2016年某某省某某市湖里区中考数学模拟试卷一、选择题(本大题有10小题,每小题4分,共40分.每小题都有四个选项,其中有且只有一个选项正确)1.的相反数是()A.B.C.3 D.﹣32.一组数据6,6,6,6,6,添加一个数0后,方差将会()A.变大 B.变小 C.不变 D.无法确定3.下列不等式组中解集为x<1的是()A.B.C.D.4.如图,在平面直角坐标系中,直线OA过点A(3,4),则tanα的值是()A.B.C.D.5.下列运算正确的是()A.20=0 B.=±2 C.2﹣1=D.23=66.如图,AB是半圆的直径,∠ABC=50°,点D是的中点,则∠DAB等于()A.40° B.50° C.65° D.70°7.事件“反比例函数y=(k>0)经过点(0,3)”的概率是()A.0 B.C.D.18.在△ABC中,若点D为AB中点,点E是AC上一点,则下列条件能判断线段DE一定为△ABC中位线的是()A.DE⊥AC B.CE=2AEC.=1 D.=9.经过以下一组点可以画出函数y=2x图象的是()A.(0,0)和(2,1)B.(1,2)和(﹣1,﹣2)C.(1,2)和(2,1)D.(﹣1,2)和(1,2)10.在△ABC中,∠B=2∠C,则AC与2AB之间的大小关系是()A.AC>2AB B.AC=2AB C.AC≤2AB D.AC<2AB二、填空题(本大题有6小题,每小题4分,共24分)11.方程x2=2x的解是.12.已知山的坡度i=1:3,若小明在爬山过程中的铅直高度上升了30米,则他在水平方向移动米.13.某次数学考试中,一学习小组的四位同学A,B,C,D的平均分是80分,为了让该小组成员之间能更好的互帮互学,老师调入了E同学,调入后,他们五人本次的平均分变为90分,则E同学本次考试为分.14.若a=1954×1946,b=1957×1943,c=1949×1951,则a,b,c的大小关系为(用“<”连接).15.如图,点A、B、C、D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=度.16.利用勾股定理可以顺次作出,,,…的线段.例如要作长为的线段,可以利用如下等式:()2=()2+1=()2+()2=22+()2=42﹣32来构造直角三角形.若k是大于1的正整数,请你通过构造一个两边均为有理数的直角三角形,作出长为的线段,则这个直角三角形的两边可以为:,.三、解答题(本大题有11小题,共86分)17.计算:+﹣x.18.如图,在平面直角坐标系中,已知点A(1,0),B(3,2),请在图中画出线段AB,并在y轴上找一点P,使得PA=PB.(要求:尺规作图,并保留作图痕迹)19.如图,点C在线段AE上,BC∥DE,AC=DE,BC=CE.求证:∠A=∠D.20.如图,某校在开展积极培育和践行社会主义核心价值观的活动中,小光同学将自己需要加强的“文明”、“友善”、“法治”、“诚信”的价值取向文字分别贴在4X质地、大小完全一样的硬纸板上,制成卡片,随时提醒自己要做个遵纪守法的好学生.小光同学还把卡片编成一道数学题考同桌小亮:将这4X卡片洗匀后背面朝上放在桌子上,从中随机抽取一X卡片,不放回,再随机抽取另一X卡片,让小亮同学用列表法或画树状图法,求出两次抽到卡片上的文字含有“文明”、“诚信”价值取向的概率(卡片名称可用字母表示).21.如图,在△ABC中,点D是AB边的三等分点(AD<BD),DE∥BC交AC于点E,DF∥AC 交BC于点F,求的值.22.某某林芝米林县与某某某校开展共建活动,为了让某某的同学也能读到更多好书,小红同学把自己多年积攒的零花钱5005元计划买300本书送给他们.其中含某某凤凰出版的A 类书《中国历史》,一本20元,某某科技出版的B类书《初中数学解题思路与方法》,一本15元,如果购买的A类书少于B类书的一半,请问小红同学的钱够不够,并说明理由.23.如图,在平面直角坐标系中,已知点A(1,1),点B在直线y=1上,点C(2+,4),点D(2,4),且∠D=∠B,试判断四边形ABCD的形状,并证明你的结论.24.已知点M为抛物线y=x2+bx+b的顶点,抛物线与x轴无交点,点N在抛物线的对称轴上且位于点M上方.若点N到点M的距离是点M到x轴距离的两倍,直线ON的解析式为y=kx,请求出k关于b的函数关系式.25.阅读以下证明过程:已知:在△ABC中,∠C≠90°,设AB=c,AC=b,BC=a.求证:a2+b2≠c2.证明:假设a2+b2=c2,则由勾股定理逆定理可知∠C=90°,这与已知中的∠C≠90°矛盾,故假设不成立,所以a2+b2≠c2.请用类似的方法证明以下问题:已知:a,b是正整数,若关于x的一元二次方程x2+2a(1﹣bx)+2b=0有两个实根x1和x2,求证:x1≠x2.26.△ABC是⊙O的内接三角形,BC=.(1)如图1,若AC是⊙O的直径,∠BAC=60°,延长BA到点D,使得DA=BA,过点D作直线l⊥BD,垂足为点D,请将图形补充完整,判断直线l和⊙O的位置关系并说明理由.(2)如图2,∠B=120°,点D是优弧的中点,DE∥BC交BA延长线于点E,BE=2,请将图形补充完整并求AB的值.27.已知点A(m,n)在反比例函数y1=上.(1)若m=,点M(0,3)且S△AOM=6,求点A的坐标;(2)若m=n=2,点A到直线y2=﹣x+b的距离为,点B(p,q)在y2=﹣x+b上,过点B 作BC⊥x轴,垂足为点C,交y1于点D.当0<p<q时,求p•BD的取值X围.2016年某某省某某市湖里区中考数学模拟试卷参考答案与试题解析一、选择题(本大题有10小题,每小题4分,共40分.每小题都有四个选项,其中有且只有一个选项正确)1.的相反数是()A.B.C.3 D.﹣3【考点】相反数.【分析】根据相反数的概念解答即可.【解答】解:的相反数是﹣,添加一个负号即可.故选B.2.一组数据6,6,6,6,6,添加一个数0后,方差将会()A.变大 B.变小 C.不变 D.无法确定【考点】方差.【分析】方差:一组数据中各数据与它们的平均数的差的平方的平均数,叫做这组数据的方差,依此定义可知方差将会变大.【解答】解:一组数据6,6,6,6,6,添加一个数0后,方差将会变大.故选A.3.下列不等式组中解集为x<1的是()A.B.C.D.【考点】解一元一次不等式组.【分析】根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定每个不等式组的解集即可.【解答】解:A、的解集为:x<1;B、无解;C、的解集为:x>2;D、的解集为:1<x<2;故选:A.4.如图,在平面直角坐标系中,直线OA过点A(3,4),则tanα的值是()A.B.C.D.【考点】锐角三角函数的定义;坐标与图形性质.【分析】根据锐角的正切等于对边比邻边,可得答案.【解答】解:如图,tanα==,故选:D.5.下列运算正确的是()A.20=0 B.=±2 C.2﹣1=D.23=6【考点】负整数指数幂;算术平方根;零指数幂.【分析】根据负整数指数幂、算术平方根、零指数幂的定义和计算公式分别对每一项进行判断即可.【解答】解:A、20=1,故本选项错误;B、=2,故本选项错误;C、2﹣1=,故本选项正确;D、23=8,故本选项错误;故选C.6.如图,AB是半圆的直径,∠ABC=50°,点D是的中点,则∠DAB等于()A.40° B.50° C.65° D.70°【考点】圆周角定理.【分析】连结BD,由于点D是AC弧的中点,即弧CD=弧AD,根据圆周角定理得∠ABD=∠CBD,则∠ABD=25°,再根据直径所对的圆周角为直角得到∠ADB=90°,然后利用三角形内角和定理可计算出∠DAB的度数.【解答】解:连结BD,如图,∵点D是的中点,即弧CD=弧AD,∴∠ABD=∠CBD,∵∠ABC=50°,∴∠ABD=×50°=25°,∵AB是半圆的直径,∴∠ADB=90°,∴∠DAB=90°﹣25°=65°.故选C.7.事件“反比例函数y=(k>0)经过点(0,3)”的概率是()A.0 B.C.D.1【考点】反比例函数的图象;概率公式.【分析】根据反比例函数的定义解答即可.【解答】解:因为反比例函数y=(k>0),x不能等于0,所以点(0,3)不在反比例函数y=(k>0)上,所以事件“反比例函数y=(k>0)经过点(0,3)”的概率是0,故选A.8.在△ABC中,若点D为AB中点,点E是AC上一点,则下列条件能判断线段DE一定为△ABC中位线的是()A.DE⊥AC B.CE=2AEC.=1 D.=【考点】三角形中位线定理.【分析】可先假设DE∥BC,由三角形中位线定理进而可得出结论.【解答】解:根据题意可假设DE∥BC,则可得△ADE∽△ABC,∵点D为AB中点,DE∥BC,∴DE是△ABC中位线,∴,∴,故选D.9.经过以下一组点可以画出函数y=2x图象的是()A.(0,0)和(2,1)B.(1,2)和(﹣1,﹣2)C.(1,2)和(2,1)D.(﹣1,2)和(1,2)【考点】正比例函数的图象.【分析】分别把各点坐标代入函数y=2x进行检验即可.【解答】解:A、∵当x=2时,y=4,∴点(2,1)不符合,故本选项错误;B、∵当x=1时,y=2;当x=﹣1时,y=﹣2,∴两组数据均符合,故本选项正确;C、∵当x=2时,y=4≠1,∴点(2,1)不符合,故本选项错误;D、∵当x=﹣1时,y=﹣2≠2;当x=1时,y=4≠2,∴两组数据均不符合,故本选项错误.故选B.10.在△ABC中,∠B=2∠C,则AC与2AB之间的大小关系是()A.AC>2AB B.AC=2AB C.AC≤2AB D.AC<2AB【考点】三角形三边关系;三角形的外角性质.【分析】延长CB到D,使DB=AB,连接AD,从而可得到∠BAD=∠D,再根据三角形的外角的性质可推出∠ABC=2∠D,从而不难得到△ADC是等腰三角形,根据三角形三边关系即可得到2AB与AC的关系.【解答】解:如图,延长CB到D,使DB=AB,连接AD,∵在△ABD中,AB=BD,∴∠BAD=∠D,∵∠ABC是△ABD的外角,∴∠ABC=2∠D,∵∠ABC=2∠C,∴∠C=∠D,∴AD=AC,在△ABD中,AB+BD>AD=AC,即2AB>AC.故选D.二、填空题(本大题有6小题,每小题4分,共24分)11.方程x2=2x的解是x1=0,x2=2 .【考点】解一元二次方程﹣因式分解法.【分析】先移项得到x2﹣2x=0,再把方程左边进行因式分解得到x(x﹣2)=0,方程转化为两个一元一次方程:x=0或x﹣2=0,即可得到原方程的解为x1=0,x2=2.【解答】解:∵x2﹣2x=0,∴x(x﹣2)=0,∴x=0或x﹣2=0,∴x1=0,x2=2.故答案为x1=0,x2=2.12.已知山的坡度i=1:3,若小明在爬山过程中的铅直高度上升了30米,则他在水平方向移动90 米.【考点】解直角三角形的应用﹣坡度坡角问题.【分析】根据斜坡AB的坡度i=1:3,可得BC:AC=1:3,将BC=30米代入求出AC的长度.【解答】解:∵斜坡AB的坡度i=1:3,∴BC:AC=1:3,∵BC=30米,∴AC=30×3=90(米).故答案为:90.13.某次数学考试中,一学习小组的四位同学A,B,C,D的平均分是80分,为了让该小组成员之间能更好的互帮互学,老师调入了E同学,调入后,他们五人本次的平均分变为90分,则E同学本次考试为130 分.【考点】加权平均数.【分析】根据一学习小组的四位同学A,B,C,D的平均分是80分,可以求得这四位同学的总分,根据老师调入了E同学,调入后,他们五人本次的平均分变为90分,可以求得这五位同学的总分,从而可以求得E的分数,本题得以解决.【解答】解:由题意可得,A,B,C,D四位同学的总分是:80×4=320分,A,B,C,D,E五位同学的总分是:90×5=450分,∴E同学的分数是:450﹣320=130分,故答案是:130.14.若a=1954×1946,b=1957×1943,c=1949×1951,则a,b,c的大小关系为c>a>b (用“<”连接).【考点】有理数大小比较.【分析】根据平方差公式,可得答案.【解答】解:a=1954×1946==19502﹣16,b=1957×1943==19502﹣49,c=1949×1951==19502﹣1,c>a>b,故答案为:c>a>b.15.如图,点A、B、C、D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD= 60 度.【考点】圆周角定理;平行四边形的性质.【分析】由四边形OABC为平行四边形,根据平行四边形对角相等,即可得∠B=∠AOC,由圆周角定理,可得∠AOC=2∠ADC,又由内接四边形的性质,可得∠B+∠ADC=180°,即可求得∠B=∠AOC=120°,∠ADC=60°,然后由三角形外角的性质,即可求得∠OAD+∠OCD的度数.【解答】解:法一:连接DO并延长,∵四边形OABC为平行四边形,∴∠B=∠AOC,∵∠AOC=2∠ADC,∴∠B=2∠ADC,∵四边形ABCD是⊙O的内接四边形,∴∠B+∠ADC=180°,∴3∠A DC=180°,∴∠ADC=60°,∴∠B=∠AOC=120°,∵∠1=∠OAD+∠ADO,∠2=∠OCD+∠CDO,∴∠OAD+∠OCD=(∠1+∠2)﹣(∠ADO+∠CDO)=∠AOC﹣∠ADC=120°﹣60°=60°.故答案为:60.法二:连接OB∵四边形OABC为平行四边形∴AB=OC=OB=OA=BC∴△OAB和△OBC都为等边三角形∴∠OAB=∠OCB=60°∵ABCD为圆的内接四边形∴∠DAB+∠DCB=180°∴∠OAD+∠OCD=180°﹣60°﹣60°=60°16.利用勾股定理可以顺次作出,,,…的线段.例如要作长为的线段,可以利用如下等式:()2=()2+1=()2+()2=22+()2=42﹣32来构造直角三角形.若k是大于1的正整数,请你通过构造一个两边均为有理数的直角三角形,作出长为的线段,则这个直角三角形的两边可以为:, 1 .【考点】勾股定理;勾股定理的逆定理.【分析】根据题目中提供的信息以及勾股定理解答即可.【解答】解::()2=()2+1=()2+()2=22+()2=42﹣32,∴()2=()2﹣12(k是大于1的正整数),∴这个直角三角形的两边可以为,1,故答案为:,1.三、解答题(本大题有11小题,共86分)17.计算:+﹣x.【考点】分式的加减法.【分析】原式通分并利用同分母分式的加减法则计算即可得到结果.【解答】解:原式===1.18.如图,在平面直角坐标系中,已知点A(1,0),B(3,2),请在图中画出线段AB,并在y轴上找一点P,使得PA=PB.(要求:尺规作图,并保留作图痕迹)【考点】作图—基本作图.【分析】在坐标系内描出A、B两点,作出线段AB,作线段AB的垂直平分线交y轴于点P,则点P即为所求.【解答】解:如图所示;19.如图,点C在线段AE上,BC∥DE,AC=DE,BC=CE.求证:∠A=∠D.【考点】全等三角形的判定与性质.【分析】利用SAS可证△ABC≌△CDE,从而可得∠A=∠D.【解答】证明:∵BC∥DE,∴∠BCA=∠CED,在△ABC与△CED中,,∴△ABC≌△CED(SAS),∴∠A=∠D20.如图,某校在开展积极培育和践行社会主义核心价值观的活动中,小光同学将自己需要加强的“文明”、“友善”、“法治”、“诚信”的价值取向文字分别贴在4X质地、大小完全一样的硬纸板上,制成卡片,随时提醒自己要做个遵纪守法的好学生.小光同学还把卡片编成一道数学题考同桌小亮:将这4X卡片洗匀后背面朝上放在桌子上,从中随机抽取一X卡片,不放回,再随机抽取另一X卡片,让小亮同学用列表法或画树状图法,求出两次抽到卡片上的文字含有“文明”、“诚信”价值取向的概率(卡片名称可用字母表示).【考点】列表法与树状图法.【分析】先画树状图展示所有12种等可能的结果数,再找出两次抽到卡片上的文字含有“文明”、“诚信”价值取向的结果数,然后根据概率公式求解.【解答】解:画树状图为:共有12种等可能的结果数,其中两次抽到卡片上的文字含有“文明”、“诚信”价值取向的结果数为2,所以两次抽到卡片上的文字含有“文明”、“诚信”价值取向的概率==.21.如图,在△ABC中,点D是AB边的三等分点(AD<BD),DE∥BC交AC于点E,DF∥AC 交BC于点F,求的值.【考点】相似三角形的判定与性质.【分析】根据已知条件得到四边形DECF是平行四边形,根据平行四边形的性质得到DE=CF,根据相似三角形的性质即可得到结论.【解答】解:∵DE∥BC交AC于点E,DF∥AC交BC于点F,∴四边形DECF是平行四边形,∴DE=CF,∵D是AB边的三等分点,∴,∵DE∥BC,∴△ADE∽△ABC,∴=,∴=.22.某某林芝米林县与某某某校开展共建活动,为了让某某的同学也能读到更多好书,小红同学把自己多年积攒的零花钱5005元计划买300本书送给他们.其中含某某凤凰出版的A 类书《中国历史》,一本20元,某某科技出版的B类书《初中数学解题思路与方法》,一本15元,如果购买的A类书少于B类书的一半,请问小红同学的钱够不够,并说明理由.【考点】一元一次方程的应用.【分析】可设A类书买了x本,则B类书买了,根据等量关系:A类书的钱数+B类书的钱数=5005元,不等量关系:购买的A类书<B类书的一半,列出方程和不等式求解即可.【解答】解:设A类书买了x本,则B类书买了,依题意有20x+15=5005,解得x=101,x<,解得x<100,∵101>100,∴小红同学的钱够.23.如图,在平面直角坐标系中,已知点A(1,1),点B在直线y=1上,点C(2+,4),点D(2,4),且∠D=∠B,试判断四边形ABCD的形状,并证明你的结论.【考点】坐标与图形性质.【分析】连接AC,由点C、D的纵坐标相同可得出直线CD的解析式,由点A的坐标以及点B 所在的直线即可得出直线AB的解析式,从而得出AB∥CD,进而可得出∠ACD=∠CAB,由此即可证出△ACD≌△CAB(AAS),根据全等三角形的性质即可得出AB=CD、AD=CB,再利用两点间的距离公式即可求出AD=CD,从而得出四边形ABCD为菱形.【解答】解:四边形ABCD为菱形,理由如下:连接AC,如图所示.∵点C(2+,4),点D(2,4),∴直线CD的解析式为y=4,∵点A(1,1),点B在直线y=1上,∴直线AB的解析为y=1,∴CD∥AB,∴∠ACD=∠CAB.在△ACD和△CAB中,,∴△ACD≌△CAB(AAS),∴AB=CD,AD=CB.∵A(1,1),C(2+,4),D(2,4),∴AD==,CD=2+﹣2=,∴AD=CD,∴AB=BC=CD=AD,∴四边形ABCD为菱形.24.已知点M为抛物线y=x2+bx+b的顶点,抛物线与x轴无交点,点N在抛物线的对称轴上且位于点M上方.若点N到点M的距离是点M到x轴距离的两倍,直线ON的解析式为y=kx,请求出k关于b的函数关系式.【考点】抛物线与x轴的交点;待定系数法求二次函数解析式.【分析】利用配方法求出点M坐标,根据条件求出点N坐标代入y=kx,求出k,再根据△<0确定b的取值X围即可.【解答】解:y=x2+bx+b=(x+)2+,∴点M坐标(﹣,),抛物线对称轴x=﹣,∴点N的横坐标为﹣,点N的纵坐标为+=,∴N(﹣,),代入y=kx得到k×(﹣)=,∴k=b﹣6,∵抛物线与x轴无交点,∴△=b2﹣4b<0,∴0<b<4,∴k=b﹣6 (0<b<4).25.阅读以下证明过程:已知:在△ABC中,∠C≠90°,设AB=c,AC=b,BC=a.求证:a2+b2≠c2.证明:假设a2+b2=c2,则由勾股定理逆定理可知∠C=90°,这与已知中的∠C≠90°矛盾,故假设不成立,所以a2+b2≠c2.请用类似的方法证明以下问题:已知:a,b是正整数,若关于x的一元二次方程x2+2a(1﹣bx)+2b=0有两个实根x1和x2,求证:x1≠x2.【考点】反证法.【分析】假设x1=x2,则方程x2﹣2abx+2a+2b=0有两个相等的实数根,即判别式△=0,据此即可得到a和b的关系,然后根据a、b是正整数从而得到错误的结论,从而证明△=0错误,得到所证的结论.【解答】证明:假设x1=x2,则方程x2﹣2abx+2a+2b=0有两个相等的实数根,∴△=4a2b2﹣8a﹣8b=4a2b2﹣4(2a+2b)=0,则a2b2=2a+2b,a2b2=2(a+b).∵a、b是正整数,∴2(a+b)是偶数,∴a2b2也是偶数,又∵a、b为正整数,∴a、b中必有一个是2的倍数,不妨设a是偶数,即a是2的倍数,则a2是4的倍数.∴a2b2是4的倍数.∴a+b是2的倍数.∵a是2的倍数,a2b2=2(a+b),∴=a+b,=,=+.∵a、b是偶数,∴位正偶数,∴+为正整数.又∵a、b位偶数,∴a=b=2,此时,a2b2=16,而2(a+b)=8,a2b2≠2(a+b)与事实不符.∴△≠0,即x1≠x2.26.△ABC是⊙O的内接三角形,BC=.(1)如图1,若AC是⊙O的直径,∠BAC=60°,延长BA到点D,使得DA=BA,过点D作直线l⊥BD,垂足为点D,请将图形补充完整,判断直线l和⊙O的位置关系并说明理由.(2)如图2,∠B=120°,点D是优弧的中点,DE∥BC交BA延长线于点E,BE=2,请将图形补充完整并求AB的值.【考点】直线与圆的位置关系.【分析】(1)作OF⊥l于F,CE⊥l于E,设AD=a,则AB=2AD=2a,只要证明OF是梯形ADEC 的中位线即可解决问题.(2)只要证明△EDA≌△BDC,得AE=BC,即可解决问题.【解答】解:(1)图形如图所示,直线l与⊙O相切.理由:作OF⊥l于F,CE⊥l于E,∵AC是直径,∴∠ABC=90°,∵DE⊥BD,∴∠BDE=90°,∴BD⊥DE,∴AD∥OF∥CE,∵AO=OC,∴DF=FE,∴OF=(AD+CE),设AD=a,则AB=2AD=2a,∵∠ABC=∠BDE=∠CED=90°,∴四边形BDEC是矩形,∴CE=BD=3a,∴OF=2a,∵在Rt△ABC中,∠ABC=90°,∠ACB=30°,AB=2a,∴AC=4a,∴OF=OA,∴直线l是⊙O切线.(2)图形如图2所示,连接AD,BD,CD.∵=,∠ABC=120°,∴∠EBD=∠CBD=60°,∵DE∥CB,∴∠ABC+∠E=180°,∴∠E=60°,∴△BED是等边三角形,∴∠EDB=60°,ED=DB,∵∠ACD=∠ABD=60°,∠DAC=∠CBD=60°,∴△ACD是等边三角形,∴∠ADC=60°,DA=DC,∴∠EDB=∠ADC,∴∠EDA=∠BDC,在△EDA和△BDC中,,∴△EDA≌△BDC,∴AE=BC=,∵BE=2,∴AB=BE﹣AE=2﹣.27.已知点A(m,n)在反比例函数y1=上.(1)若m=,点M(0,3)且S△AOM=6,求点A的坐标;(2)若m=n=2,点A到直线y2=﹣x+b的距离为,点B(p,q)在y2=﹣x+b上,过点B 作BC⊥x轴,垂足为点C,交y1于点D.当0<p<q时,求p•BD的取值X围.【考点】反比例函数与一次函数的交点问题.【分析】(1)根据待定系数法求出k,再根据三角形面积公式可以确定点A横坐标,由此即可解决问题.(2)如图,首先判断直线y2在点A上方,点B在线段EF上运动(不包括点E),构建二次函数即可解决问题.【解答】解:(1)∵点A(m,n)在反比例函数y1=上,且m=,∴k=mn=1,∴y=,∵点M(0,3),∴OM=3,∵S△AOM=6,∴A的横坐标为±4,∴m=±4,∵n=,∴A(4,)或(﹣4,﹣);(2)如图,直线OA与y2交于点E,∵AE=,A(2,2),∴K=4,y=,∴点E坐标(3,3),∵点B(p,q)在y2=﹣x+b上,过点B作BC⊥x轴,垂足为点C,交y1于点D.0<p<q,∴点B在点E上方,点F下方,∴p•BD=p(﹣p+6﹣)=﹣p2+6p﹣4=﹣(p﹣3)2+5,∴p•BD的最大值为5,当点B与点F重合时取得最小值0,∵0<p<q,∴p≠3,∴0≤p•BD<5.。

福建省中等职业学校学生学业水平考试公共基础知识考试大纲I.考试性质中等职业学校学生学业水平考试是根据国家及省中等职业学校教学标准及考试要求,由省教育厅组织实施的考试,主要衡量中等职业学校学生达到专业学习要求的程度,是保障中等职业学校教育教学质量的重要措施。
学业水平考试成绩是学生毕业和升学的重要依据,是评价和改进学校教学工作的重要参考,是检验中等职业学校教学质量的重要方式,是开展中等职业学校办学能力诊断与评估的重要考核指标。
Ⅱ.考试内容德育福建省德育课程学业水平考试旨在检测中等职业学校学生对德育课程知识的认知、理解和运用的水平。
一、考试目标与要求德育课程学业水平考试注重考查学生对德育课程基础知识的认知、认同和运用知识分析问题、解决问题的能力。
了解:要求对某一知识和原理,能够再认、再现,即知道“是什么”。
理解:要求对某一知识和原理能够较全面、较深入地领会,并分析、解释现象,辨明正误,即明白“为什么”。
运用:指在理解的基础上,能运用知识对具体问题作出分析、判断和提出解决方案,即清楚“怎么办”。
二、考试范围与要求本考试的范围为《中等职业学校德育课程教学大纲》规定的四门必修课程:《职业生涯规划》、《职业道德与法律》、《经济政治与社会》、《哲学与人生》。
根据课程教学大纲和学生成长与发展的实际需求,对四门必修课程内容进行了必要的整合。
考试的具体内容和要求如下:必修一:职业生涯规划1.1了解职业、职业生涯和职业理想的内涵;1.2了解职业生涯规划以及中职生职业生涯规划的特点;1.3 理解职业理想对职业生涯发展的重要性;2.1了解专业和专业对应的职业群;2.2了解职业素养的内涵;2.3了解职业资格证书对职业生涯发展的重要性;2.4了解兴趣对职业生涯发展的作用;2.5 结合所学专业培养职业兴趣;2.6了解性格对职业生涯发展的作用;2.7 结合所学专业调适自己的职业性格;2.8了解能力对职业生涯发展的作用;2.9 结合所学专业提高职业能力;2.10 了解职业价值取向的内容;2.11 学会从实际出发调整职业价值取向;2.12 结合所学专业了解关注行业发展动向;3.1 了解职业生涯发展目标的构成;3.2理解职业生涯发展目标与发展条件的关系;3.3 学会运用职业生涯发展目标的选择方法,确立自己的职业生涯发展目标;3.4 了解职业生涯阶段目标的特点及设计思路;3.5 理解近期目标是职业生涯规划中最重要的阶段目标;3.6 学会运用近期目标的制定要领,制定近期目标;3.7 理解职业生涯发展措施的重要性和制定要领;3.8 学会运用职业生涯发展措施的制定要素,根据职业生涯发展目标,制定近期目标的计划;4.1了解正确的就业观念;4.2 学会认清就业形势、树立“先就业再择业”的观念,为将来求职就业准确定位做准备;4.3了解就业信息的内容;4.4学会结合自身实际获取、甄别、筛选有效的就业信息;4.5掌握求职面试技巧,为求职就业做准备;4.6 理解创业的意义、创业者应具备的素质和能力;4.7培养、提升创业能力,做好创业准备;5.1 了解调整职业生涯规划的必要性及方法;5.2了解终身学习与职业生涯发展的关系。
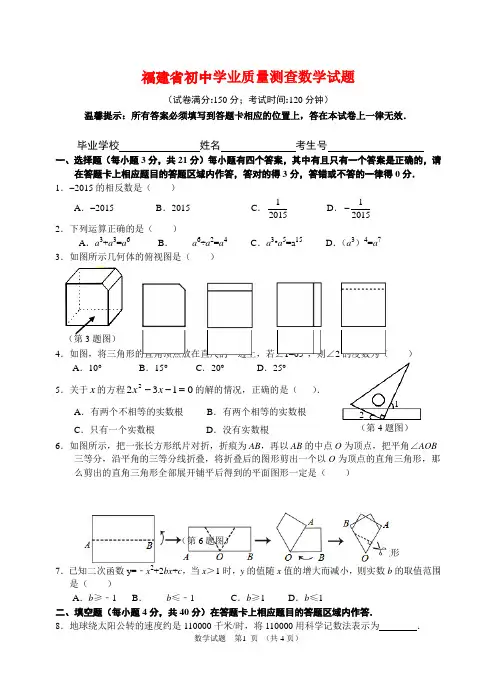
福建省初中学业质量测查数学试题(试卷满分:150分;考试时间:120分钟)温馨提示:所有答案必须填写到答题卡相应的位置上,答在本试卷上一律无效.毕业学校 姓名 考生号一、选择题(每小题3分,共21分)每小题有四个答案,其中有且只有一个答案是正确的,请在答题卡上相应题目的答题区域内作答,答对的得3分,答错或不答的一律得0分. 1.-2015的相反数是( )A .-2015B .2015C .12015 D .12015- 2.下列运算正确的是( )A .a 3+a 3=a 6B . a 6÷a 2=a 4C .a 3•a 5=a 15D .(a 3)4=a 73.如图所示几何体的俯视图是( )A .B .C .D . 4.如图,将三角形的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为( ) A .10° B .15° C .20° D .25° 5.关于x 的方程01322=--x x 的解的情况,正确的是( ).A .有两个不相等的实数根B .有两个相等的实数根C .只有一个实数根D .没有实数根6.如图所示,把一张长方形纸片对折,折痕为AB ,再以AB 的中点O 为顶点,把平角∠AOB三等分,沿平角的三等分线折叠,将折叠后的图形剪出一个以O 为顶点的直角三角形,那么剪出的直角三角形全部展开铺平后得到的平面图形一定是( )A .正三角形B .正方形C .正五边形D .正六边形7.已知二次函数y=﹣x 2+2bx +c ,当x >1时,y 的值随x 值的增大而减小,则实数b 的取值范围是( )A .b ≥﹣1B . b ≤﹣1C .b ≥1D .b ≤1二、填空题(每小题4分,共40分)在答题卡上相应题目的答题区域内作答.8.地球绕太阳公转的速度约是110000千米/时,将110000用科学记数法表示为 .(第3题图) (第4题图)(第6题图)219.若正n 边形的中心角等于24°,则这个正多边形的边数为 . 10.分解因式:x x 42+ = .11.若a <13<b ,且a ,b 为连续正整数,则b 2﹣a 2= .12. 计算:_______x yx y x y +=++.13.在《中国梦•我的梦》演讲比赛中,由6个评委对某选手打分,得分情况如下:8,9,7,8,9,10 (单位:分),则该选手得分的中位数是 分. 14. 不等式组⎩⎨⎧≤-≥+0201x x 的解集是 . 15.菱形ABCD 的边长AB =5cm ,则菱形ABCD 的周长为 cm .16.如图,P A 、PB 是⊙O 的切线,切点是A 、B ,已知60P ∠=︒,P A =63,那么AB 的长为 .17.如图放置的△OAB 1,△B 1A 1B 2,△B 2A 2B 3,…都是边长为2的等边三角形,边AO 在y 轴上,点B 1,B 2,B 3,…都在直线kx y =上,则(1)k = ,(2)A 2015的坐标是 . 三、解答题(共89分)在答题卡上相应题目的答题区域内作答. 18.(9分)计算:10)31(28)2(|3|-+⨯--+-π.19.(9分)先化简,再求值:)22(2)2(2-++a a a ,其中3=a .20.(9分)如图,已知:点B 、F 、C 、E 在一条直线上,∠B =∠E ,BF =CE ,AB =DE .求证:△ABC ≌△DEF .21.(9分)为了解我县八年级学生参加社会实践活动情况,随机抽查了部分八年级学生第一学期参加社会实践活动的天数,并用得到的数据绘制了两幅统计图,下面给出了两幅不完整的统计图(如图所示).A OP B(第16题图)ECABDFA 1A 2 A OB 1 B 2B3 AO BP (第17题图)请根据图中提供的信息,解答下列问题:(1)直接填写:a =____%,该扇形所对圆心角的度数为____度,并补全条形图;(2)如果全县共有八年级学生7000人,请你估计“活动时间不少于...7天”的学生人数大约有多少人?22.(9分)第14届亚洲艺术节计划于2015年11月底在泉州举行.现有20名志愿者准备参加某分会场的工作,其中男生8人,女生12人. (1)若从这20人中随机选取一人作为联络员,直接写出选到女生的概率;(2)若该分会场的某项工作只在甲、乙两人中选一人,他们准备以游戏的方式决定由谁参加,游戏规则如下:将四张牌面数字分别为2,3,4,5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则甲参加,否则乙参加.试问这个游戏公平吗?请用树状图或列表法说明理由.23.(9分)已知反比例函数xm y 1-=(m 为常数)的图象在第一、三象限内. (1)求m 的取值范围;(2)如图,若该反比例函数的图象经过平行四边形ABOD 的顶点D ,点A 、B 的坐标分别为a(0,3),(﹣2,0).①求出该反比例函数解析式;②设点P 是该反比例函数图象上的一点,且在ΔDOP 中,OD=OP ,求点P 的坐标. 24.(9分)甲,乙两辆汽车分别从A ,B 两地同时出发,沿同一条公路相向而行,乙车出发2小时后休息,与甲车相遇后,继续行驶.设甲,乙两车与B 地的路程分别为y 甲(km ),y 乙(km ),甲车行驶的时间为x (h ),y 甲,y 乙与x 之间的函数图象如图所示,结合图象解答下列问题: (1)乙车休息了 h ;(2)求乙车与甲车相遇后y 乙与x 的函数解析式,并写出自变量x 的取值范围;(3)当两车相距40km 时,求出x 的值.25.(13分)如图,已知抛物线c bx x y ++-=221图象经过A (﹣1,0),B (4,0)两点. (1)求抛物线的解析式;y/km y(2)若C (m ,m ﹣1)是抛物线上位于第一象限内的点,D 是线段AB 上的一个动点(不与端点A 、B 重合),过点D 分别作DE ∥BC 交AC 于E ,DF ∥AC 交BC 于F .①求证:四边形DECF 是矩形; ②试探究:在点D 运动过程中,DE 、DF 、CF 的长度之和是否发生变化?若不变,求出它的值;若变化,试说明变化情况.A O D BF EC x26.(13分)在平面直角坐标系中,O 为坐标原点,直线33+-=k kx y 交y 轴正半轴于点A ,交x 轴于点B (如图1)(1)不论k 取何值,直线AB 总经过一个定点C ,请直接写出点C 坐标; (2)当OC ⊥AB 时,求出此时直线AB 的解析式;(3)如图2,在(2)条件下,若D 为线段AB 上一动点(不与端点A 、B 重合),经过O 、D 、B 三点的圆与过点B 垂直于AB 的直线交于点E ,求ΔDOE 面积的最小值.(图1)(图2)参考答案及评分标准说明:(一)考生的正确解法与“参考答案”不同时,可参照“参考答案及评分标准”的精神进行评分.(二)如解答的某一步出现错误,这一错误没有改变后续部分的考查目的,可酌情给分,但原则上不超过后面应得的分数的二分之一;如属严重的概念性错误,就不给分.(三)以下解答各行右端所注分数表示正确做完该步应得的累计分数. 一、选择题(每小题3分,共21分) 1.B 2.B 3.C 4.D 5.A 6.A 7.D 二、填空题(每小题4分,共40分)8. 5101.1⨯ 9. 15 10. )4(+x x 11.7 12. 1 13. 8.5 14. 21≤≤-x 15. 20 16. π4 17.(1)33(2))2017,32015( 三、解答题(共89分) 18.(本题9分)解:原式=3+1-4+3…………………………………………………………8分 =3…………………………………………………………………… 9分 19.(本题9分)解:原式=a a a a 444422-+++…………………………………………………4分=452+a ………………………………………………………………6分当3=a 时,原式=4)3(52+⨯………………………………………7分=19…………………………………………………9分 20.(本题9分)证明:∵CE BF =, ∴CF CE CF BF +=+即EF BC =……………4分又∵E B DE AB ∠=∠=,……………7分 ∴△ABC ≌△DEF . ………………………9分21.(本题9分)解:(1)10,36°,补图如右;(填空各2分,补图2分, 共6分)(2)7000×(25%+10%+5%)=7000×40%=2800人. 答:“活动时间不少于7天”的学生人数大约有2800人……………………9分 22. (本题9分)ECA BDF解 :(1)P (女生)=53;……………………………………………………3分 (2)解法一: 画树状图…………………………………………………………………………6分由树状图可知,共有12种机会均等的情况,其中和为偶数的有4种情况,P ∴(甲参加)=31124=,P (乙参加)=32128=. P (甲参加)<P (乙参加), ∴这个游戏不公平. ……………………………………………………9分 解法二:列表(略)23. (本题9分)解:(1)根据题意得01>-m解得1>m …………………3分(2)①∵四边形ABOC 为平行四边形, ∴AD ∥OB ,AD =OB =2 又A 点坐标为(0,3)∴D 点坐标为(2,3)………………5分∴1-m =2×3=6∴反比例函数解析式为xy 6=………………6分 ②(法一)如图所示,以O 为圆心,OD 长为半径作圆O ,与双曲线xy 6=分别交于321,,,P P P D 四点. 根据图形的对称性,得点D (2,3)关于直线y =x 对称点1P 的坐标为(3,2);………………7分 点D (2,3)关于原点中心对称点2P 的坐标为(﹣2,﹣3);点1P (3,2)关于原点中心对称点3P 的坐标为(﹣3,﹣2). ………….8分 由于O 、D 、2P 三点共线.,所以符合题意的P 点只有两点, 其坐标分别为(3,2),(﹣3,﹣2). …………..9分(法二)2 第1张第2张 3 4 53 4 52 4 52 3 52 3 4和 5 6 7 5 7 8 6 7 9 7 8 9∵直线y =x 是反比例函数x y 6=图象的对称轴, D (2,3)在反比例函数xy 6=图象上, ∴点D (2,3)关于直线y =x 对称点的坐标为(3,2),则此时满足条件OP =OD 的P 点坐标为(3,2)………………..7分 ∵反比例函数xy 6=的图象是以原点为对称中心的中心对称图形 ∴当点P 与点D 关于原点中心对称,则OD =OP ,但此时O 、D 、P 三点共线. 而点(3,2)关于原点中心对称的点的坐标为(﹣3,﹣2)即此时满足条件OP =OD 的P 点坐标为(﹣3,﹣2)…………………8分综上,符合题意的P 点有两点,其坐标分别为(3,2),(﹣3,﹣2).………………9分 24. (本题9分)解:(1)0.5;………………………3分(2)设乙车与甲车相遇后y 乙与x 的函数解析式y 乙=kx +b ,y 乙=kx +b 图象过点(2.5,200),(5,400),得⎩⎨⎧=+=+4005,2005.2b k b k 解得⎩⎨⎧==0,80b k ∴乙车与甲车相遇后y 乙与x 的函数解析式y 乙=80x (2.5≤x ≤5);………………6分(其中自变量取值范围1分)(3)设乙车与甲车相遇前y 乙与x 的函数解析式y 乙=kx ,图象过点(2,200),所以200=2k 解得k =100 ∴乙车与甲车相遇前y 乙与x 的函数解析式y 乙=100x可求y 甲与x 的函数解析式y 甲=-80x +400…………………7分 ①当0≤x <2.5时,y 甲减y 乙等于40千米即﹣80x +400﹣100x =40,解得 x =2………………………8分 ②当2.5≤x ≤5时,y 乙减y 甲等于40千米即80x ﹣(﹣80x +400)=40,解得x =…………………9分综上,x =2或x =.25. (本题13分) 解:∵抛物线y=﹣221x +bx +c 图象经过A (﹣1,0),B (4,0)两点, 根据题意,得⎪⎩⎪⎨⎧++-=+--=c b c b 480,210 解得⎪⎩⎪⎨⎧==.2,23c b ∴抛物线的解析式为:223212++-=x x y ;…………3分(2)①证明:把C (m ,m ﹣1)代入223212++-=x x y 得 2232112++-=-m m m ,解得:m =3或m =﹣2,∵C (m ,m ﹣1)位于第一象限,∴⎩⎨⎧-01,0 m m ∴m >1,∴m =﹣2不合舍去,只取m =3, ∴点C 坐标为(3,2),…………4分(法一)如图,过C 点作CH ⊥AB ,垂足为H ,则∠AHC =∠BHC =90°, 由A (﹣1,0)、B (3,0)、C (3,2)得 AH =4,CH =2,BH =1,AB =5 ∵,2==BH CH CH AH ∠AHC =∠BHC =90°∴△AHC ∽△CHB ,∴∠ACH =∠CBH , ∵∠CBH +∠BCH =90°∴∠ACH +∠BCH =90°∴∠ACB =90°,…………6分 ∵DE ∥BC ,DF ∥AC ,即四边形DECF 是平行四边形,…………7分 ∴四边形DECF 是矩形;…………8分 (法二)∵202=AC ,52=BC ,AB =5, ∴222AB BC AC =+=25, ∴∠ACB =90°.以下解法同上.(法三)由1-=∙BC AC k k ,证得∠ACB =90°. 以下解法同上.(3)(法一) ∵DE ∥BC ∴ΔAED ∽ΔACB ∴AB AD BC ED = (1)…………9分同理:ABBDAC DF =(2) 设n AD =, 则n BD -=5由(1)得55n ED =………10分∴55nED FC ==由(2)得5)5(52n DF -=………11分 ∴52=++FC DF ED ………12分∴DE 、DF 、CF 的长度之和不变. …………13分(法二)∵DE ∥BC ∴ΔAED ∽ΔACB∴AB AD BC ED = (1)…………9分 同理:ABBDAC DF =(2) 由(1)+(2)得:1=+ACDF BC ED …………10分又∵5,52==BC AC ,CF =ED ∴522=+DF ED …………11分 ∴52=++FC DF ED ………12分∴DE 、DF 、CF 的长度之和不变. …………13分26. (本题13分)解:(1))3,3(C …………3分(2)(法一)如图,作CF ⊥OB 于F ,则3=OF ,CF =3 在Rt ΔOCF 中,tan ∠COF =333==OF CF∴∠COF = 60………4分又∵AB OC ⊥∴∠ABO = 30………5分在Rt ΔBCF 中,tan ∠ABO =33=BF CF ∴33=BF ∴34=OB ∴)0,34(B …………6分 把)0,34(B 代入33+-=k kx y ,得33-=k …………7分 ∴433+-=x y …………8分(法二)由BF OF CF ∙=2,得33=BF(法三)设B )0,(a ,由222OB CB OC =+,得22222)3(33)3(a a =-+++ 解得34=a(法四)可求直线OC 解析式为x y 3=,由AB OC ⊥,得13-=k ,∴33-=k(3)∵O 、D 、B 、E 四点共圆∴ 180=∠+∠DBE DOE ……………………9分又∵AB ⊥BE ∴ 90=∠ABE ∴ 90=∠DOE∵ 30=∠=∠ABO DEO ……………………10分在Rt ΔDOE 中,tan ∠DEO =33=OE OD ∴OD OE 3= ∴22321OD OE OD S DOE =∙=∆……………………11分 ∴当OD ⊥AB 时,ΔDOE 的面积最小,即点D 与点C 重合, 此时32==OC OD ……………………12分∴ΔDOE 面积的最小值为36.……………………13分。
厦门市湖滨中学2016—2017学年第一学期期中考试卷初二历史(试卷满分100分,考试时间60分钟)注意事项:1.全卷五大题,37小题,试卷共4页。
2.答案一律写在答卷上,否则不能得分。
一、单项选择(本大题共30小题,每小题2分,共60分,每小题只有一个选项符合题意)1.鸦片战争爆发的根本原因是( )A.中国人民虎门销烟 B.打开中国大门以倾销商品,掠夺原料C.林则徐下令停止中英贸易 D.占领香港岛作为侵略中国建立据点2.人民英雄纪念碑浮雕记载了近代重大革命斗争事件,最早的历史事件是( ) A.虎门销烟 B.五四运动 C.百万雄师过大江D.辛亥革命3.鸦片战争后中国的社会性质是( )A.仍然是独立的封建社会 B.半殖民地半封建社会C.殖民地社会 D.资本主义社会4.道光帝接受林则徐等人禁烟的主张是因为( )A.鸦片摧残人的身体 B.坚持闭关锁国政策C.鸦片输入威胁清朝统治 D.整顿吏治的需要5.鸦片战争后,外国人在中国长江口所获得的通商口岸为( )A.宁波 B.福州 C.广州 D.上海6.曾被称之为“万园之园”的圆明园如今只剩下断壁残垣,造成这种结果的罪魁祸首是( ) A.英美联军 B.英俄联军 C.英法联军 D.美俄联军7.19世纪上半期,西方最强大的资本主义是( )A.美国 B.法国 C.英国 D.西班牙8.太平天国建立起与清朝对峙的政权的标志是( )A.金田起义 B.定都天京 C.永安改制 D.天京陷落9.“洋枪队”协助清军攻打太平军说明了( )A.太平军要把外国人赶出中国 B.清政府雇佣了外国军队C.清军有了洋枪洋炮 D.外国侵略者和清政府勾结起来10.义和团运动兴起和发展的原因是( )A.西方列强掀起的瓜分中国的狂潮 B.自然灾害严重C.清政府的残暴统治 D.八国联军的侵略11.第二次鸦片战争期间,沙俄侵略中国的野心主要是( )A.扩大市场 B.攫取赔款 C.鸦片贸易 D.侵占领土12.下列关于第一、二次鸦片战争的说法正确的是( )①外国资本主义强国为打开中国市场而发动的②都是资本主义列强为瓜分中国发动的③都发生在19世纪④两次战争的侵略者都有英国A.①②③ B.①②③④ C.①②④ D.①③④13.“此日漫挥天下泪,有公足壮海军威”赞誉的此“公”是( )A.邓世昌 B.林则徐 C.左宝贵 D.丁汝昌14.《马关条约》的签订“表明外国资本主义对中国的经济侵略从此进入一个新的阶段”,最主要的表现是( )A.赔偿白银二亿两 B.割台湾及其附近岛屿给日本C.开放重庆沙市等为通商口 D.允许日本在中国开设工厂15.清政府完全成为列强统治中国的工具是在( )A.鸦片战争后 B.第二次鸦片战争后C.甲午中日战争后 D.八国联军侵华战争后16.洋务派主张利用西方的先进技术,欲达到的目的是( )A.发展中国科技 B.强兵富国、维护清朝的统治C.平定内乱 D.抵御外国的侵略17.小兰曾在洋务派创办的第一所新式学堂学习过,你知道这所学堂的名称吗( ) A.福建船政学堂 B.京师同文馆 C.万木草堂 D.北洋水师学堂18.若想了解李鸿章创办的民用企业的情况,可查阅哪个企业的资料( )A.江南制造总局 B.福州船政局 C.轮船招商局 D.湖北织布局19.一位记者在采访一位农民时问道:“目前,你最大的心愿是什么?”农民说:“我的心愿与洋务运动后期提出的口号一致。
厦门中考成绩折算方法中考成绩在学生的学业发展中扮演着重要的角色,对于学生升学和未来的发展具有决定性的影响。
由于不同的地区和学校所使用的评分标准有所不同,为了公平、公正地评价学生的中考成绩,厦门市制定了一套科学的折算方法,以确保学生的成绩能够得到准确而公正的评价。
本文将详细介绍厦门市中考成绩折算方法,并通过举例进行说明,以帮助大家更好地理解。
一、折算方法的目的和原则:为了保证中考成绩的准确性和公平性,厦门市制定了一套科学的折算方法。
该方法的目的是消除不同学校之间评分标准的差异,使得学生的成绩能够在不同学校之间公正比较。
折算方法的原则包括公平、科学、客观和可操作性,以确保学生的成绩能够真实反映他们的学业水平和潜力。
二、折算方法的步骤:1. 确定基准分数线:首先,厦门市教育局会根据全市中考的整体成绩水平,确定一条基准分数线。
该基准分数线是全市中考成绩的平均线,用于划定及格线和优秀线的分界点,并作为折算方法的参考。
2. 收集原始成绩数据:学校会将学生的原始中考成绩提交给教育局进行数据收集。
这些原始成绩包括各科目的得分情况以及相应的等级。
3. 数据标准化处理:为了将不同学校的成绩进行比较,需要对原始成绩进行标准化处理。
标准化处理的目的是将原始成绩转化为相对数值,使得各个学校的成绩能够在同一评价尺度下进行比较。
常见的标准化方法包括Z分数和T分数等。
4. 成绩折算:基于标准化后的成绩数据,采用折算公式对学生的成绩进行折算和调整。
具体的折算方法取决于不同的学校和学科,但都会考虑到原始成绩的权重和标准分数的相对分布情况。
5. 阈值调整:有些学校可能会对不同科目的成绩设置特定的阈值标准。
厦门市教育局会根据学生的成绩分布情况,适当调整阈值,以保证公平和合理。
三、举例说明:以某高中为例,该校使用折算方法对学生的语文和数学成绩进行评价。
学生甲的原始成绩如下:语文:88分数学:92分1. 根据厦门市教育局的要求,学校先将学生的原始成绩进行标准化处理。
2016年福建省厦门市中考数学试卷一、选择题(本大题 10小题,每小题4分,共40分)1. 1°等于( )A. 10' B . 12' C . 60' D . 100'22 .方程x - 2x=0的根是() A. x 1 =x 2=0 B . x 1=x 2=2 C. x 1=0, x 2=2 D. x 1=0, x 2= - 23.如图,点 E , F 在线段BC 上,△ ABF 与厶DCE 全等,点 A 与点D,点B 与点C 是对应顶点, AF 与过点C 作CF// BD 交DE 的延长线于点F ,则下列结论正确的是 (6.已知甲、乙两个函数图象上部分点的横坐标x 与对应的纵坐标y 分别如表所示,两个函数图象仅有一个交点,则交点的纵坐标y 是( ) 甲 B .- 5 V x w 3 C. x >- 5 D. x V 3/ AFB(2s<64 .不等式组(”,的解集是(A . - 5W x V 3 CF V BD D. EF > DEy 0 2A. 0B. 1C. 2D. 37 .已知△ ABC的周长是I , BC=l - 2AB,则下列直线一定为△ ABC的对称轴的是()A.\ ABC的边AB的垂直平分线B. Z ACB的平分线所在的直线C. A ABC的边BC上的中线所在的直线D. A ABC的边AC上的高所在的直线&已知压强的计算公式是段时间后,就好变钝,如果刀刃磨薄, 刀具就会变得锋利•下列说法中,能正确解释刀具变得锋利这一现象的是()A. 当受力面积一定时,压强随压力的增大而增大B. 当受力面积一定时,压强随压力的增大而减小C. 当压力一定时,压强随受力面积的减小而减小D. 当压力一定时,压强随受力面积的减小而增大9•动物学家通过大量的调查估计,某种动物活到现年20岁的这种动物活到25岁的概率是(A. 0.8B. 0.75 C . 0.6 D. 0.4820岁的概率为0.8,活到25岁的概率为0.6,则)10. 设681 X 2019- 681 X 2018=a, 2015X 2016- 2013 X 2018=b,呂?+[ 358+690+6T呂二£,贝a,b, c的大小关系是()A. b v c v aB. a v c v bC. b v a v cD. c v b v a、填空题(本大题有6小题,每小题4分,共24分)11. 不透明的袋子里装有2个白球,1个红球,这些球除颜色外无其他差别,从袋子中随机摸出1个球,则摸出白球的概率是________,我们知道,刀具在使12.化简:13 .如图,在△ ABC中,DE// BC,且AD=2 DB=3 则近似值公式得到 U2 _x3 二 M 2屋12 iW —- + ;…依此算法, 所得 匸的近似值会越来越精确.当k 「I 取得近似值』一时,近似公式中的a 是15.已知点P (m n )在抛物线y=ax 2- x - a 上,当m >- 1时,总有nW 1成立,则a 的取值范围是16.如图,在矩形 ABCD 中,AD=3以顶点D 为圆心,1为半径作O D,过边BC 上的一点P 作射线PQ M 连接AP,若AP+PQ 駆|,/ APB=/ QPC 则/ QPC 的大小约 sin11 ° 32' 1 ,tan36° 52'=三、解答题(共86分)17 .计算: 伽鲜(尹剳牛片gL5 18 .解方程组丿d , _ .4買+y 二-呂19.某公司内设四个部门,2015年各部门人数及相应的每人所创年利润如表所示,求该公司 年平均每人所创年利润.2015部门 人数 每人所创年利润/ 14•公元3世纪,我国古代数学家刘徽就能利用近似公式 計备得到的近似值•他的算法 是:先将回看出心^寸:由近似公式得到 厉切朽打二;再将匝看成J (上,由与O D 相切于点Q,且交边AD 于点611y=1,求此函数的解析式,并在平面直角坐标系中画出此22.如图,在△ ABC 中,/ ACB=90 , AB=5, BC=4,将厶ABC绕点C 顺时针旋转 90°,若点 A , B 的对应点分别是点 D, E ,画出旋转后的三角形,并求点 A 与点D之间的距离.(不要求尺规作图)后的时间x (小时)变化的图象(图象由线段 O A 与部分双曲线AB 组成)•并测得当 y=a 时,该药物才具有疗效.若成人用药 4小时,药物开始产生疗效,且用药后 9小时,药物仍具有疗效,则成 万元3627 16OC=OE / C=25,求证:AB// CD/ BCD 是钝角,AB=AD BD 平分/ ABC 若 CD=3 BD=V] 24.如图,是药品研究所所测得的某种新药在成人用药后,血液中的药物浓度 y (微克/毫升) 用药 D 20 函数图象.3,sin / DB人用药后,血液中药物浓则至少需要多长时间达到最大度?25.如图,在平面直角坐标系中xOy中,已知点A (1, m+1 , B (a, m+1), C (3, m+3), D( 1,m+a , m> 0, 1v a v 3,点P (n - m n)是四边形ABCD内的一点,且△卩人。
福建省厦门市2016年初中毕业及高中阶段各类学校招生考试物理答案解析一、选择题 1.【答案】C【解析】滑雪板面积很大、书包的背带很宽、坦克的履带很宽都是通过增大受力面积从而减小压强的;切果器的切片很薄是通过减小受力面积从而增大压强。
正确的是C 。
【考点】压强的改变方式。
2.【答案】D【解析】厦门岛内禁止燃放烟花爆竹,是从声源处减弱噪声,A 不合题意;鼓浪屿禁止商家导游使用扩音器,是从声源处减弱噪声,B 不符合题意;地铁施工时给机器加润滑油,是为了防止机器振动发声,是从声源处减弱噪声,C 不符合题意;部分BRT 路段两侧设有透明板墙,是从传播过程中减弱噪声,D 符合题意。
【提示】减弱噪声的途径有:在声源处减弱、在传播过程中减弱、在人耳处减弱。
【考点】减弱噪声的方法。
3.【答案】D【解析】空间实验室内适宜宇航员工作生活的气压与地球上的气压相近,大约为100000Pa ,正确选项为D 【考点】大气压强。
4.【答案】A【解析】此时荷叶上水珠中间厚,边缘薄,相当于凸透镜;当透过附在荷叶上的水珠观察荷叶时,叶子相当于在该水凸透镜的1倍焦距以内,即此时可以成一个正立、放大的虚像,故此时叶片上细密的纹理变得清晰可辨,故选A 。
【提示】解读凸透镜的成像规律:u 2f >,成倒立、缩小的实像;2f u f >>,成倒立、放大的实像;u f <,成正立、放大的虚像。
【考点】凸透镜成像的应用。
5.【答案】B【解析】剪开较硬的物体,需要省力的剪刀,因此需选用动力臂大于阻力臂的剪刀,即柄比刀口长的剪刀,故选B 。
【考点】杠杆的分类。
6.【答案】A【解析】当人在触摸静电球时,由于电子的转移,人身体就会带上电荷,即人的头发上会带上同种电荷,由于同种电荷相互排斥,此时人的头发会飘起来,故选A 。
【提示】解读在自然界中只有两种电荷,即正电荷和负电荷,且电荷间存在着相互作用规律,即同种电荷相互排斥,异种电荷相互吸引。
中考考试说明12篇中考考试说明12篇中考考试说明1 1:场地器材规格及设置要求考试的场地应在封闭的、标准400米田径场上进展,考试所需的标志线明晰,起点线和终点线应该设置明显的标志。
考试采用径赛电动计时系统,系统应符合田径竞赛规那么要求。
考试前考务人员必须对场地标准和器材的准确性进展检查。
将电动计时系统的硬件架设在耐久跑的起点和终点,起点架设实时监控系统,系统使用时会拍摄各组考生的起跑和终点的图像,考生对自己的成绩存在争议时可追溯查取。
2:考试操作标准及要求考务员负责将考生按小组带至起点,起点检录逐一核对考生身份(刷卡或条码枪扫描),派发号码背心或其它标识物,监视学生正确穿好号码背心或其它标识物,检查无误后进入考试程序。
学生上道准备好后,发令裁判与终点计时电脑操作员协调确定发令时机,发令裁判按下无线语音发令装置“发令”按钮,发令装置自动发出起跑语音口令,同时无线触发终点计时电脑开场计时,终点计时电脑操作员负责监视起跑计时启动以及跑步过程中的计时、计圈和图像采集,考生跑完全程计时系统自动锁定其成绩并记录冲刺图像;测试完毕后,学生成绩显示在成绩确认电脑上。
学生刷卡可以确认和保存成绩。
成绩按秒表的分、秒记录,缺乏一秒不计入成绩。
假如考生对成绩出现异议,可以回放测试图像进展追溯。
每个考生只有一次考试时机,每组考生人数假设干人。
考生应采用站立式起跑,弧形起跑线出发,起跑口令发出前越过起跑线为犯规。
起跑后不分跑道。
跑程中不得踏进跑道左侧跑道线,不得推、拉、阻挡别人跑进,不得由别人带跑。
3:考生的犯规行为a.发令前,踩踏或越过起跑线;b.跑进中踏进跑道左侧跑道线;c.跑进中推、拉、阻挡别人跑进;d.跑进中由别人领跑,或借入别人的力量跑进。
4:考生考前须知a.考生考试时穿胶底运动鞋,不得穿钉子鞋或皮鞋。
b. 跑程中不得踏进跑道左侧跑道线,不得推、拉、阻挡别人跑进,不得由别人带跑。
中考考试说明2 期中考试转眼过去,而我也在悲伤和欢乐中度过。
厦门市2016年初中生学业考试说明地理
厦门市教育科学研究院基教室制定
2016年3月
2016年福建省厦门市初中毕业、升学考试
地理学科考试说明
一、考试性质
初中地理学业考试是义务教育初中阶段的终结性省级考试,是一种标准参照考试,其目的是全面、准确地评价初中毕业生是否达到《义务教育地理课程标准(2011年版)》(以下简称《课标》)所规定的学业水平。
根据《厦门市2016年高中阶段各类学校招生工作方案》的规定,地理属于中考考试科目,考试成绩将按卷面成绩依考生总数的4:3:2: 1的比例分别折合为A、B、C、D四个等级,参与高中录取等级计算。
初中生地理学业考试结果,既是衡量学生是否达到毕业标准的主要依据,也是高中阶段学校招生的重要依据。
二、命题依据
以《课标》为指导,以《2016年福建省初中学业考试大纲(地理)》及本《考试说明》为依据进行命题。
三、命题原则
(一)导向性原则
坚持以立德树人为核心,强化考试内容的育人导向。
加强社会主义核心价值观的考查,指引学生培养正确的世界观、人生观和价值观;加强依法治国理念的考查,引导学生树立宪法意识和法治观念;加强中国优秀传统文化的考查,引导学生提高人文素养、传承民族精神、
弘扬爱国主义,树立民族自信心和自豪感;加强创新能力的考查,促进创新教育。
坚持以学生为本,立足基础,注重能力培养,做到区域性、综合性、思想性、生活性、实践性的统一,正确发挥考试的导向功能,转变教师的教学方式和学生的学习方式,推动初中学校全面实施新课程、培养学生的创新精神和实践能力。
(二)基础性原则
注重地理基础知识和基本技能的考查,主要包括学生对地理位置、地理概念、地理特征、地理空间分布、区域差异等方面的理解,以及学生能否在具体情境中调动已有地理基础知识,合理应用地理基本技能,解决地理问题。
淡化特殊的解题技巧,不出偏题、怪题。
(三)科学性原则
试题设计与本《考试说明》要求一致,具有较高的信度、效度。
试卷结构合理,内容科学严谨,文字简洁、规范,答案准确合理。
注重地理学科核心素养,考查人地协调观的形成、区域认知、综合思维和地理实践力。
有效地发挥各种类型题目的功能。
例如,考查学生对于地理事物的记忆能力,可以设计填图、填充、选择类试题;考查学生从具体情境中获取地理信息的能力,可以设计读图、阅读分析类试题;考查学生解决地理问题的能力,可以设计具有实际背景的试题;考查学生的探究、创造能力,可以设计开放性试题。
四、考试范围
地球与地图、世界地理、中国地理、厦门地理。
五、适用范围
2016年厦门市全日制义务教育初二(八年级)学生。
六、考试目标要求
(一)考查目标
1.知识目标
2.技能与能力目标
3.情感态度价值观目标
(二)能力层级
七、考试内容与要求
依据《课标》规定的课程内容与要求,确定以下考试内容与要求。
(一)地理基础知识(地理记忆能力)
(二)地理基本技能和能力
第一部分地球与地图⒈地球和地球仪
⒉地图
第二部分世界地理
⒉气候
⒊居民
⒋地域发展差异
第三部分中国地理⒈疆域与人口
认识区域部分建议主要讲授东北地区、新疆维吾尔自治区和课标要求的必学区域(北京、台湾、香港和澳门)。
第四部分厦门地理
运用地图,描述厦门市的地理位置,分析其特点。
【】
在厦门市政区空白图上,指出厦门市区级行政区。
【】
利用图文材料说明厦门市主要地理事物的变迁及其原因。
【】
举例分析自然资源、自然灾害对厦门市社会、经济等方面的影响。
【】
运用厦门市的人口资料与全国人口情况进行比较,说出厦门市人口数量和人口变化的特点。
【】
了解厦门市的对外联系现状,认识厦门市进一步改革开放的重要性。
在厦门市空白地图上指出对外联系的主要交通干线。
【】了解厦门市的发展规划。
厦门市规划发展成为“现代化国际性港口风景旅游城市”,从自然条件、自然资源、社会经济发展水平三方面,简要分析其具备的优越条件。
【】
八、试卷结构
(一)题型分值比例:单项选择题50%,综合题50%。
(二)内容分值比例:地球地图约15%;世界地理约30%;中国地理约45%~50%;厦门地理约5%~10%。
(三)试题易中难分值比例:控制在7∶2∶1左右。
试题按难度值分为容易题、中等题和难题。
难度值P≥的为容易题;难度值≤P <的为中等题;难度值P<的为难题。
九、其他说明
(一)整卷难度:控制在~。
(二)及格率:控制在~。
(三)试卷总分:100分。
(四)考试时间:60分钟。
(五)考试形式:闭卷笔答考试,分为试卷与答题卡两部分,考生必须将答案全部写在答题卡上。
(六)基本题型:单项选择题、非选择题。
1.单项选择题是以图文材料为背景设计的四选一型的单项选择题。
2.非选择题是以图文材料为背景设计的填图、填充、判断、连线、读图分析、阅读分析、绘图等题型的总称。
十、试题示例
选择题举例:
图7示意我国干湿地区分布,读图完成19~22题。
19.福建省位于()
A.干旱区 B.半干旱区
C.湿润地区 D.半湿润区
20.甲区域的年降水量大约为()
A.<100毫米B.100~200毫米
C.200~400毫米D.400~800毫米
21.乙区域的主要植被是()
A.森林 B.森林草原
C.草原 D.荒漠
22.M河流与N河流共同的水文特征是()
A.夏季汛期 B.流量较大
C.有结冰期 D.含沙量小
【命题意图与试题解析】
本题组意在用一幅中国干湿地区的分布图,
考查学生的四种能力。
即对省区空间分布的识记(记忆能力)、读图用图能力、逻辑推理能力和综合分析问题的能力。
第19题,难度较易,以学生生活的省区为例,了解省区的分布。
第20题,难度较大,要求学生能将所学知识进行综合概括,找出知识点之间的内在关联,运用一定的逻辑思维推理,推导出正确答案。
第21题,难度中等,命题的目的是让学生能根据图例得知图中甲、乙两区域所属干湿地区,判断其年降水量的多少,再结合不同降水量影响下形成的土地利用类型进行分析,最后得出乙区域的主要植被是什么这一结论。
第22题,难度较大,学生首先要有一定的知识储备,要掌握河流的水文特征,在此基础上能运用比较的方式,找出内外流河共性的
水文特征。
【参考答案】 19. C 20. D 21. C 22. A
非选择题举例:
29.图14示意长江水系,读图完成下列问题。
(10分)
(1)长江发源于青海省的_________山脉,注入________海。
(2)长江因__________价值高,被誉为“黄金水道”。
其上游蕴藏
丰富的可再生能源是_________。
这是因为长江上游________大,
而且_________也大。
(3)三峡水利枢纽是世界最大的水利枢纽,具有航运、
、
等综合效益。
(4)图中,L 河段泥沙淤积严重,造成这一现象的自然原因是河道
弯曲,流速________;人为原因是森林遭到破坏,______________
严重,导致含沙量增大。
【命题意图】
让学生通过阅读长江水系图和荆江河段形态示意图,了解长江的
源流概况及其在我国经济发展中的作用。
命题依据课程标准,以能力立意为导向,体现地理学科的特点。
整题的顺序先易后难,结构平衡,梯度合理,利于学生正常发挥。
图
【试题解析】
第1小题,考查长江源流概况,难度较低,让学生通过读图完成相关内容,旨在培养学生运用地图的能力。
第2小题考查长江的水文特征及影响,难度中等,旨在学生应用能力的提升,进而培养学生的地理思维能力。
第3小题考查长江三峡这一大型水利工程修建对中国经济发展所产生的综合影响,难度较高,具有一定的实践意义,可体现学生的地理实践能力。
第4小题考查长江流域的水文特征与人类活动对地理环境的影响,难度中等,旨在训练学生的应用能力和运用地图的能力。
【参考答案】
(1)唐古拉山脉、东海
(2)航运、水能、落差大、水量大
(3)防洪、发电、灌溉、养殖、旅游等
(4)流速减缓、水土流失加剧。