工程力学第7章 弯曲强度答案
- 格式:doc
- 大小:782.50 KB
- 文档页数:14


工程力学(第2版)第7章 弯 曲题 库: 主观题7-1 长度为250mm ,截面尺寸为0.8mm 25mm h b ⨯=⨯的薄钢板卷尺,由于两端外力偶的作用而弯成中心角为030的圆弧。
已知弹性模量52.110MPa E =⨯。
试求钢尺横截面上的最大正应力。
解:由题知302250mm 360πρ⋅= ,故480mm ρ= 卷尺最外层纤维应变最大,且为4max 0.428.3310480hερ-===⨯ 由拉压胡克定律可知 54max max 2.1108.3310176MPa E σε-==⨯⨯⨯=即钢尺横截面上的最大正应221(0.250.23)760.573kN /m 4q π=-⨯=力为176MPa .知识点:1.梁横截面的应力。
参考页: P145。
学习目标: 2(掌握梁横截面上的应力计算方法,会利用应力计算公式计算正应力) 难度: 1.0提示一:该题考察知识点:1. 梁横截面上的应力计算。
提示二:无 提示三:无 提示四(同题解) 题解:1、利用正应力计算公式计算正应力。
7-2 一外径为250mm ,壁厚为10mm ,长度l=12m 的铸铁水管,两端搁在支座上,管中充满着水,如图所示。
铸铁的容量3176kN /m γ=,水的容重3210kN /m γ=。
试求管内最大拉、压正应力的数值。
解:每米铸铁水管的重量 每米水柱的重量22220.2310.231100.415kN /m 44q y ππ=⨯⨯⨯=⨯⨯⨯=故水管所受均布荷载120.988kN /m q q q =+=在水管中部有弯矩最大值22max 110.9881217.784kN m 88M ql ==⨯⨯=⋅最大弯曲正应力为3max max343217.7841040.7MPa 2300.25[1()]250z M W σπ⨯⨯===⨯⨯-故管内最大拉、压正应力的数值为,max ,max 40.7MPa t c σσ==。
知识点:1.梁横截面的应力。
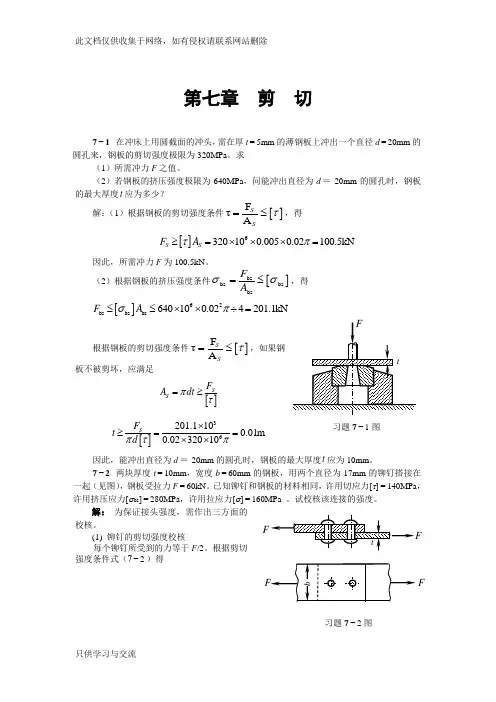
此文档仅供收集于网络,如有侵权请联系网站删除第七章 剪 切7−1 在冲床上用圆截面的冲头,需在厚t =5mm 的薄钢板上冲出一个直径d =20mm 的圆孔来,钢板的剪切强度极限为320MPa 。
求(1)所需冲力F 之值。
(2)若钢板的挤压强度极限为640MPa ,问能冲出直径为d =20mm 的圆孔时,钢板的最大厚度t 应为多少?解:(1)根据钢板的剪切强度条件[]F τA SSτ=≤,得 []6320100.0050.02100.5kN S S F A τπ≥=⨯⨯⨯=因此,所需冲力F 为100.5kN 。
(2)根据钢板的挤压强度条件[]bsbs bs bsF A σσ=≤,得 []62bs bs bs 640100.024201.1kNF A σπ≤≤⨯⨯÷=根据钢板的剪切强度条件[]F τA SSτ=≤,如果钢板不被剪坏,应满足[]SS F A dt πτ=≥[]36201.1100.01m 0.0232010S F t d πτπ⨯≥==⨯⨯因此,能冲出直径为d =20mm 的圆孔时,钢板的最大厚度t 应为10mm 。
7−2 两块厚度t =10mm ,宽度b =60mm 的钢板,用两个直径为17mm 的铆钉搭接在一起(见图),钢板受拉力F =60kN 。
已知铆钉和钢板的材料相同,许用切应力[τ]=140MPa ,许用挤压应力[σbs ]=280MPa ,许用拉应力[σ]=160MPa 。
试校核该连接的强度。
解: 为保证接头强度,需作出三方面的校核。
(1) 铆钉的剪切强度校核每个铆钉所受到的力等于F /2。
根据剪切强度条件式(7−2)得习题7−1图习题7−2图此文档仅供收集于网络,如有侵权请联系网站删除()[]2323τ/2/430101710/4266.1MPa S SF A F πd πτ-==⨯=⨯⨯⨯=≤满足剪切强度条件。
(2) 铆钉的挤压强度校核 上、下侧钢板与每个铆钉之间的挤压力均为F bs =F /2,由于上、下侧钢板厚度相同,所以只校核下侧钢板与每个铆钉之间的挤压强度,根据挤压强度条件式7−4得[]333bs F σA F /2d t301017101010288.2MPa bs bs bs σ--==⋅⨯=⨯⨯⨯⨯=≤满足挤压强度条件。

⼯程⼒学第7章答案第7章简单的弹性静⼒学问题7-1 有⼀横截⾯⾯积为A 的圆截⾯杆件受轴向拉⼒作⽤,若将其改为截⾯积仍为A 的空⼼圆截⾯杆件,其他条件不变,试判断以下结论的正确性:(A )轴⼒增⼤,正应⼒增⼤,轴向变形增⼤;(B )轴⼒减⼩,正应⼒减⼩,轴向变形减⼩;(C )轴⼒增⼤,正应⼒增⼤,轴向变形减⼩;(D )轴⼒、正应⼒、轴向变形均不发⽣变化。
正确答案是 D 。
7-2 韧性材料应变硬化之后,材料的⼒学性能发⽣下列变化:(A )屈服应⼒提⾼,弹性模量降低;(B )屈服应⼒提⾼,韧性降低;(C )屈服应⼒不变,弹性模量不变;(D )屈服应⼒不变,韧性不变。
正确答案是 B 。
7-3 关于材料的⼒学⼀般性能,有如下结论,试判断哪⼀个是正确的:(A )脆性材料的抗拉能⼒低于其抗压能⼒;(B )脆性材料的抗拉能⼒⾼于其抗压能⼒;(C )韧性材料的抗拉能⼒⾼于其抗压能⼒;(D )脆性材料的抗拉能⼒等于其抗压能⼒。
正确答案是 A 。
7-4 低碳钢材料在拉伸实验过程中,不发⽣明显的塑性变形时,承受的最⼤应⼒应当⼩于的数值,有以下四种答案,试判断哪⼀个是正确的:(A )⽐例极限;(B )屈服强度;(C )强度极限;(D )许⽤应⼒。
正确答案是 B 。
7-5 根据图⽰三种材料拉伸时的应⼒—应变曲线,得出的如下四种结论,试判断哪⼀种是正确的:(A )强度极限)3()2()1(b b b σσσ>=,弹性模量E(1)>E(2)>E(3),延伸率δ(1)>δ(2)>δ(3)⽐例极限;(B )强度极限)2()1()3(b b b σσσ<<,弹性模量E(2)>E(1)>E(3),延伸率δ(1)>δ(2)>δ(3)⽐例极限;(C )强度极限)3()1()2(b b b σσσ>>,弹性模量E(3)>E(1)>E(2),延伸率δ(3)>δ(2)>δ(1)⽐例极限;(D )强度极限)3()2()1(b b b σσσ>>,弹性模量E(2)>E(1)>E(3),延伸率δ(2)>δ(1)>δ(3)⽐例极限;正确答案是 B 。

第一章 绪论一、是非判断题1.1 材料力学的研究方法与理论力学的研究方法完全相同。
( ) 1.2 内力只作用在杆件截面的形心处。
( ) 1.3 杆件某截面上的内力是该截面上应力的代数和。
( ) 1.4 确定截面内力的截面法,适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。
( ) 1.5 根据各向同性假设,可认为材料的弹性常数在各方向都相同。
( ) 1.6 根据均匀性假设,可认为构件的弹性常数在各点处都相同。
( ) 1.7 同一截面上正应力ζ与切应力η必相互垂直。
( ) 1.8 同一截面上各点的正应力ζ必定大小相等,方向相同。
( ) 1.9 同一截面上各点的切应力η必相互平行。
( ) 1.10 应变分为正应变ε和切应变γ。
( ) 1.11 应变为无量纲量。
( ) 1.12 若物体各部分均无变形,则物体内各点的应变均为零。
( ) 1.13 若物体内各点的应变均为零,则物体无位移。
( ) 1.14 平衡状态弹性体的任意部分的内力都与外力保持平衡。
( )1.15 题1.15图所示结构中,AD 杆发生的变形为弯曲与压缩的组合变形。
( )1.16 题1.16图所示结构中,AB 杆将发生弯曲与压缩的组合变形。
( )二、填空题1.1 材料力学主要研究 受力后发生的 ,以及由此产生的 。
1.2 拉伸或压缩的受力特征是 ,变形特征是 。
1.3 剪切的受力特征是 ,变形特征是 。
1.4 扭转的受力特征是 ,变形特征是 。
B题1.15图题1.16图1.5 弯曲的受力特征是 ,变形特征是 。
1.6 组合受力与变形是指 。
1.7 构件的承载能力包括 , 和 三个方面。
1.8 所谓 ,是指材料或构件抵抗破坏的能力。
所谓 ,是指构件抵抗变形的能力。
所谓 ,是指材料或构件保持其原有平衡形式的能力。
1.9 根据固体材料的性能作如下三个基本假设 , , 。

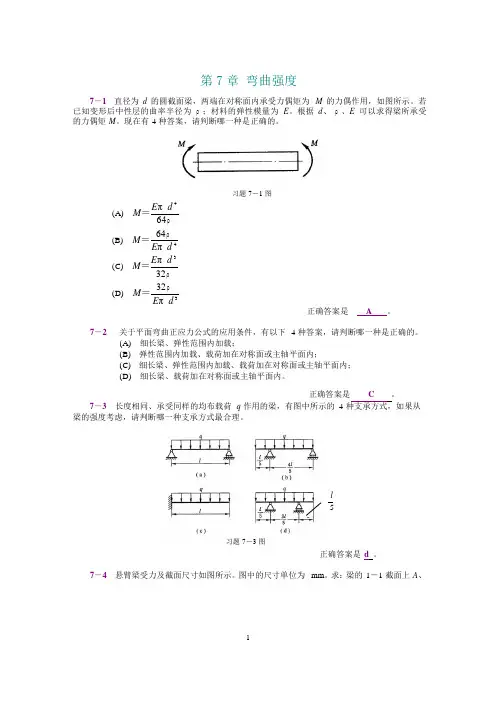
43第 7 章 弯曲强度7-1 直径为 d 的圆截面梁,两端在对称面内承受力偶矩为 M 的力偶作用,如图所示。
若已知变形后中性层的曲率半径为 ρ ;材料的弹性模量为 E 。
根据 d 、 ρ 、E 可以求得梁所承受 的力偶矩 M 。
现在有 4 种答案,请判断哪一种是正确的。
(A)M =E π d 习题 7-1 图(B) 64ρ M =64 ρ(C) E π d 4 M =E π d(D)32 ρ M = 32ρ E π d 3正确答案是 A 。
7-2关于平面弯曲正应力公式的应用条件,有以下 4 种答案,请判断哪一种是正确的。
(A) 细长梁、弹性范围内加载; (B) 弹性范围内加载、载荷加在对称面或主轴平面内; (C) 细长梁、弹性范围内加载、载荷加在对称面或主轴平面内; (D) 细长梁、载荷加在对称面或主轴平面内。
正确答案是 C _。
7-3 长度相同、承受同样的均布载荷 q 作用的梁,有图中所示的 4 种支承方式,如果从 梁的强度考虑,请判断哪一种支承方式最合理。
l 5习题 7-3 图正确答案是 d 。
7-4 悬臂梁受力及截面尺寸如图所示。
图中的尺寸单位为 mm 。
求:梁的 1-1 截面上 A 、−⎜ ⎟ A I zB 两点的正应力。
习题 7-4 图解:1. 计算梁的 1-1 截面上的弯矩:M = ⎛1×103N ×1m+600N/m ×1m ×1m ⎞ =−1300 N ⋅ m ⎝2 ⎠ 2. 确定梁的 1-1 截面上 A 、B 两点的正应力:A 点:⎛150 ×10−3 m ⎞ 1300 N ⋅ m ×⎜− 20 ×10−3m ⎟ σ = M z y = ⎝ 2 ⎠=2.54×106 Pa = 2.54 MPa (拉应力) I zB 点:100 ×10-3m ×(150 ×10-3m )3121300N ⋅ m ×⎜ 0.150m − 0.04m ⎟⎛ ⎞ σ = M z y ⎝ 2 ⎠ =1.62 ×106 Pa =1.62MPa(压应力) B ()127-5 简支梁如图所示。
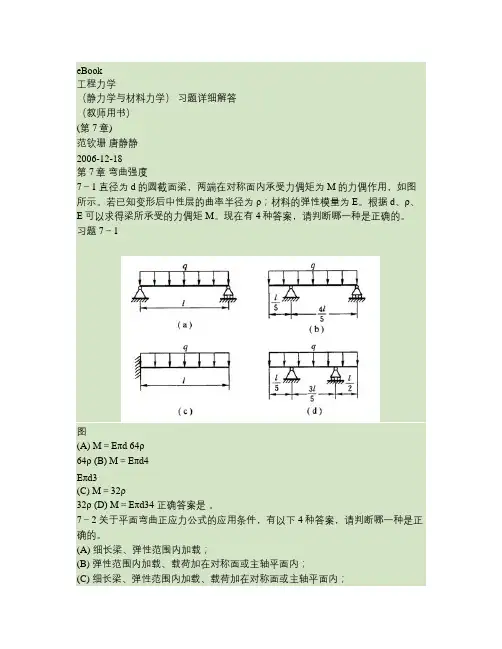
eBook工程力学(静力学与材料力学)习题详细解答(教师用书)(第7章)范钦珊唐静静2006-12-18第7章弯曲强度7-1 直径为d的圆截面梁,两端在对称面内承受力偶矩为M的力偶作用,如图所示。
若已知变形后中性层的曲率半径为ρ;材料的弹性模量为E。
根据d、ρ、E可以求得梁所承受的力偶矩M。
现在有4种答案,请判断哪一种是正确的。
习题7-1图(A) M=Eπd 64ρ64ρ (B) M=Eπd4Eπd3(C) M=32ρ32ρ (D) M=Eπd34 正确答案是。
7-2 关于平面弯曲正应力公式的应用条件,有以下4种答案,请判断哪一种是正确的。
(A) 细长梁、弹性范围内加载;(B) 弹性范围内加载、载荷加在对称面或主轴平面内;(C) 细长梁、弹性范围内加载、载荷加在对称面或主轴平面内;(D) 细长梁、载荷加在对称面或主轴平面内。
正确答案是 C _。
7-3 长度相同、承受同样的均布载荷q作用的梁,有图中所示的4种支承方式,如果从梁的强度考虑,请判断哪一种支承方式最合理。
l 5习题7-3图正确答案是7-4 悬臂梁受力及截面尺寸如图所示。
图中的尺寸单位为mm。
求:梁的1-1截面上A、 2B两点的正应力。
习题7-4图解:1. 计算梁的1-1截面上的弯矩:M=−⎜1×10N×1m+600N/m×1m×2. 确定梁的1-1截面上A、B两点的正应力:A点:⎛⎝31m⎞=−1300N⋅m 2⎟⎠⎛150×10−3m⎞−20×10−3m⎟1300N⋅m×⎜2My⎝⎠×106Pa=2.54MPa(拉应力)σA=z=3Iz100×10-3m×150×10-3m()12B点:⎛0.150m⎞1300N⋅m×⎜−0.04m⎟My⎝2⎠=1.62×106Pa=1.62MPa(压应力)σB=z=3Iz0.1m×0.15m127-5 简支梁如图所示。

第七章杆类构件的应力分析与强度计算习题7.1图示阶梯形圆截面杆AC ,承受轴向载荷1200 kN F =与2100 kN F =, AB 段的直径mm 401=d 。
如欲使BC 与AB 段的正应力相同,试求BC 段的直径。
题7.1图解:如图所示:物体仅受轴力的作用,在有两个作用力的情况下经分析受力情况有:AB 段受力:1NAB F F = BC 段受力:12NBC F F F =+AB 段正应力:1221440.04NAB NAB AB AB F F F A d σππ⨯===⨯ BC 段正应力:()12222244NBC NBC BCBC F F F F A d d σππ+⨯===⨯ 而BC 与AB 段的正应力相同 即,BC AB σσ=解出:249d mm ==7.2图示轴向受拉等截面杆,横截面面积2500 mm A =,载荷50 kN F =。
试求图示斜截面()o30=αm-m 上的正应力与切应力,以及杆内的最大正应力与最大切应力。
mm题7.2图解:拉杆横截面上的正应力605000010050010N F F Pa MPa A A σ︒-====⨯ 应用斜截面上的正应力和剪应力公式:2300cos σσα︒︒=030sin 22στα︒︒=有图示斜截面m-m 上的正应力与切应力为:3075MPa σ︒=3043.3MPa τ︒=当0=α时,正应力达到最大,其值为max 0100MPa σσ︒== 即:拉压杆的最大正应力发生在横截面上,其值为100MPa 。
当45=α时,切应力最大,其值为0max 502MPa στ︒==即拉压杆的最大切应力发生在与杆轴成45的斜截面上,其值为50MPa 。
7.3图示结构中AC 为钢杆,横截面面积21200 mm A =,许用应力[]1160 Mpa σ=;BC 为铜杆,横截面面积22300 mm A =,许用应力[]2100 Mpa σ=。
试求许可用载荷[]F 。
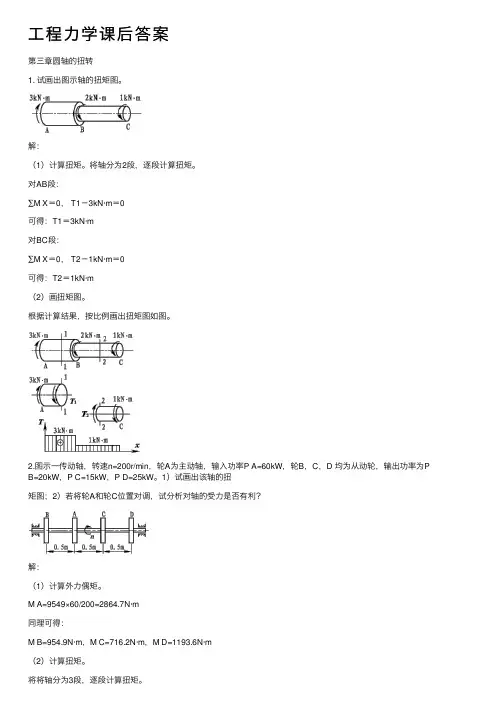
⼯程⼒学课后答案第三章圆轴的扭转1. 试画出图⽰轴的扭矩图。
解:(1)计算扭矩。
将轴分为2段,逐段计算扭矩。
对AB段:∑M X=0, T1-3kN·m=0可得:T1=3kN·m对BC段:∑M X=0, T2-1kN·m=0可得:T2=1kN·m(2)画扭矩图。
根据计算结果,按⽐例画出扭矩图如图。
2.图⽰⼀传动轴,转速n=200r/min,轮A为主动轴,输⼊功率P A=60kW,轮B,C,D 均为从动轮,输出功率为P B=20kW,P C=15kW,P D=25kW。
1)试画出该轴的扭矩图;2)若将轮A和轮C位置对调,试分析对轴的受⼒是否有利?解:(1)计算外⼒偶矩。
M A=9549×60/200=2864.7N·m同理可得:M B=954.9N·m,M C=716.2N·m,M D=1193.6N·m(2)计算扭矩。
将将轴分为3段,逐段计算扭矩。
对AB段:∑M x=0, T1+M B=0可得:T1=-954.9N·m对BC段:∑M x=0, T2+M B-M A=0可得:T2=1909.8N·m对BC段:∑M x=0, T3-M=0可得:T3=1193.6N·m(3)画扭矩图。
根据计算结果,按⽐例画出扭矩图如右图。
(4)将轮A和轮C位置对调后,由扭矩图可知最⼤绝对值扭矩较之原来有所降低,对轴的受⼒有利。
3. 圆轴的直径d=50mm,转速n=120r/min。
若该轴横截⾯的最⼤切应⼒τmax=60MPa,问圆轴传递的功率多⼤?解:W P=πd3/16=24543.7mm3由τmax=T/W P可得:T=1472.6N·m由M= T=9549×P/n可得:P=T×n/9549=18.5kW4. 在保证相同的外⼒偶矩作⽤产⽣相等的最⼤切应⼒的前提下,⽤内外径之⽐d/D=3/4的空⼼圆轴代替实⼼圆轴,问能够省多少材料?5. 阶梯轴AB如图所⽰,AC段直径d1=40mm,CB段直径d2=70mm,外⼒偶矩M B=1500N·m,M A=600N·m,M C=900N·m,G=80GPa,[τ]=60MPa,[φ/]=2(o)/m。
第七章 弯曲变形7-2 图示外伸梁AC ,承受均布载荷q 作用。
已知弯曲刚度EI 为常数,试计算横截面C 的挠度与转角,。
题7-2图 解:1. 建立挠曲轴近似微分方程并积分 支座A 与B 的支反力分别为23 ,2qaF qa F By Ay ==AB 段(0≤x 1≤a ):121122d d x EI qa x w -=121114d d C x EIqa x w +-= (a)11131112D x C x EIqa w ++-= (b)BC 段(0≤x 2≤a ):2222222d d x EI q x w -=232226d d C x EIq x w +-= (c)22242224D x C x EIq w ++-= (d)2. 确定积分常数梁的位移边界条件为 0 0 11==w x 处,在 (1)0 11==w a x 处,在(2)连续条件为2121 w w a x x ===处,在(3)221121d d d d x wx w a x x -===处,在(4)由式(b )、条件(1)与(2),得01=D , EIqa C 1231=由条件(4)、式(a )与(c ),得EI qa C 332=由条件(3)、式(b )与(d ),得EIqa D 24742-=3. 计算截面C 的挠度与转角将所得积分常数值代入式(c )与(d ),得CB 段的转角与挠度方程分别为EI qa x EI q 36332+-=2θEIqa x EI qa x EI q w 247324423422-+-=将x 2=0代入上述二式,即得截面C 的转角与挠度分别为() 33EI qa C =θ()↓-= 2474EIqa w C7-3 图示各梁,弯曲刚度EI 均为常数。
试根据梁的弯矩图与约束条件画出挠曲轴的大致形状。
题7-3图解:各梁的弯矩图及挠曲轴的大致形状示如图7-3。
图7-37-6 图示简支梁,左、右端各作用一个力偶矩分别为M 1与M 2的力偶。
一、单选题1、研究梁的变形的目的是()。
A.进行梁的正应力计算B.进行梁的刚度计算C.进行梁的稳定性计算D.进行梁的剪应力计算正确答案:B2、图示圆截面悬臂梁,若直径d增大1倍(其它条件不变),则梁的最大正应力、最大挠度分别降至原来的()。
A.1/2 1/4B.1/4 1/8C.1/8 1/8D.1/8 1/16正确答案:D3、下面关于梁、挠度和转角的讨论中,正确的结论是()。
A.挠度最大的截面转角为零B.挠度最大的截面转角最大C.转角为零的截面挠度最大D.挠度的一阶导数等于转角正确答案:D4、已知两悬臂梁的抗弯截面刚度EI相同,长度分别为l和2l,在自由端各作用F1和F2,若二者自由端的挠度相等,则F1/F2=()。
A.2B.4C.6D.8正确答案:D5、梁上弯矩为零处()。
A.梁的转角一定为零B.梁的挠度一定为零C.挠度一定为零,转角不一定为零D.梁的挠曲线的曲率一定为零正确答案:D6、已知等直梁在某段上的挠曲轴方程w(x)=–Cx4,C为常量,则在该段梁上()。
A.分布载荷是x的一次函数B.分布载荷是x的二次函数C.无分布载荷作用D.有均匀分布载荷作用正确答案:D7、在等直梁弯曲变形中,挠曲线曲率最大值发生在()。
A.剪力最大处B.转角最大处C.弯矩最大处D.挠度最大处正确答案:C8、材料相同的(a)悬臂梁和(b)悬臂梁,长度也相同,在自由端各作用2P和P,截面形状分别是b(宽)×2b(高)、b×b。
关于它们的最大挠度正确的是()。
A.(a)梁最大挠度是(b)梁的1/4倍B.(a)梁最大挠度是(b)梁的1/2倍C.(a)梁最大挠度与(b)梁的相等D.(a)梁最大挠度是(b)梁的2倍正确答案:A9、已知简支梁的EI为常数,在梁的左端和右端分别作用一力偶m1和m2今欲使梁的挠曲线在x=l/3处出现一拐点,则比值m1/m2为()。
A.2B.3C.1/2D.1/3正确答案:C10、两根梁尺寸,受力和支承情况完全相同,但材料不同,弹性模量分别为E1和E2,且E1=7E2,则两根梁的挠度之比y1/y2为()。
第七章 组合变形本章主要讨论建筑工程中常见的组合变形的强度计算问题。
其中斜弯曲、拉(压)与弯曲、偏心拉(压)组合变形的强度计算问题是本章的重点。
第一节 组合变形的概念前面的章节分别研究了杆件在轴向拉(压)、剪切、扭转、平面弯曲基本变形下的强度和刚度计算。
但在工程实际中,结构中一些杆件的受力情况是复杂的,往往同时发生两种或者两种以上的基本变形,这种由两种或两种以上的基本变形组合而成的变形称为组合变形。
例如,图7-1a 所示的烟囱,除自重引起的轴向压缩外,还有水平方向的风力引起的弯曲变形,即同时产生两种基本变形。
又如,图7-1b 所示的备有吊车的厂房柱,作用在立柱上的荷载1F 和2F ,其合力的作用线一般不在立柱轴线上,此时,立柱即发生压缩变形又发生弯曲变形。
再如,图7-1c 所示的曲拐轴,在荷载F 作用下,曲拐AB 段同时发生扭转和弯曲变形。
上述这些杆件的变形,都是结构杆件发生组合变形的工程实例。
图7-1由上一章梁的弯曲可知:外力沿横向作用在梁的纵向对称平面内,梁将发生平面弯曲变形。
那么,外力虽然沿梁的横向(垂直于轴线),但不作用在纵向对称平面内时,梁会发生怎样的变形呢?实验及理论研究得知,此时梁轴线变形后弯成的曲线已不在荷载的作用平面内,即不属于平面弯曲,这种弯曲称为斜弯曲。
若外力不沿梁的横向(斜交于轴线),但力作用仍在纵向对称平面内,梁将发生拉(压)与弯曲组合变形。
若作用外力虽然沿杆件轴向方向,但不与轴线重合,杆件也将发生拉(压)与弯曲组合变形,称为偏心拉(压)。
对发生组合变形的杆件计算应力和变形时,可将荷载进行简化或分解,使简化或分解后得到的静力等效的荷载,每类荷载各自只引起一种基本变形,分别计算,再进行叠加,就得到由原来的荷载所引起的组合变形的应力和变形,这就是组合变形的分析方法和组合变形计算的叠加原理。
这里需要强调的是:叠加原理是在满足小变形和力与位移成线性关系的条件下才适用。
本章将主要讨论斜弯曲、拉压与弯曲、偏心拉伸(压缩)组合变形的强度计算问题。
43第 7 章 弯曲强度7-1 直径为 d 的圆截面梁,两端在对称面内承受力偶矩为 M 的力偶作用,如图所示。
若已知变形后中性层的曲率半径为 ρ ;材料的弹性模量为 E 。
根据 d 、 ρ 、E 可以求得梁所承受 的力偶矩 M 。
现在有 4 种答案,请判断哪一种是正确的。
(A)M =E π d 习题 7-1 图(B) 64ρ M =64 ρ(C) E π d 4 M =E π d(D)32 ρ M = 32ρ E π d 3正确答案是 A 。
7-2关于平面弯曲正应力公式的应用条件,有以下 4 种答案,请判断哪一种是正确的。
(A) 细长梁、弹性范围内加载; (B) 弹性范围内加载、载荷加在对称面或主轴平面内; (C) 细长梁、弹性范围内加载、载荷加在对称面或主轴平面内; (D) 细长梁、载荷加在对称面或主轴平面内。
正确答案是 C _。
7-3 长度相同、承受同样的均布载荷 q 作用的梁,有图中所示的 4 种支承方式,如果从 梁的强度考虑,请判断哪一种支承方式最合理。
l 5习题 7-3 图正确答案是 d 。
7-4 悬臂梁受力及截面尺寸如图所示。
图中的尺寸单位为 mm 。
求:梁的 1-1 截面上 A 、−⎜ ⎟ A I zB 两点的正应力。
习题 7-4 图解:1. 计算梁的 1-1 截面上的弯矩:M = ⎛1×103N ×1m+600N/m ×1m ×1m ⎞ =−1300 N ⋅ m ⎝2 ⎠ 2. 确定梁的 1-1 截面上 A 、B 两点的正应力:A 点:⎛150 ×10−3 m ⎞ 1300 N ⋅ m ×⎜− 20 ×10−3m ⎟ σ = M z y = ⎝ 2 ⎠=2.54×106 Pa = 2.54 MPa (拉应力) I zB 点:100 ×10-3m ×(150 ×10-3m )3121300N ⋅ m ×⎜ 0.150m − 0.04m ⎟⎛ ⎞ σ = M z y ⎝ 2 ⎠ =1.62 ×106 Pa =1.62MPa(压应力) B ()127-5 简支梁如图所示。
试求I-I 截面上A 、B 两点处的正应力,并画出该截面上的正应力 分布图。
习题 7-5 图A(a)A(b)F R R B解:(1)求支座约束力F RA = 3.64kN,F RB = 4.36kN习题 7-5 解图(2)求I -I 截面的弯矩值(见习题7-5解图b )M I −I = 3.64kN ⋅ m(3)求所求点正应力σ = M I-I y AI z33 I = bh z12= 75 ×150 12= 21.1×106 mm 4 y A = (75 − 40) = 35mm 6∴σ = − 3.64 ×10 ×35 = −6.04MPaA 21.1×1066σ = 3.64 ×10 × 75 =12.94MPa B 21.1×1067-6 加热炉炉前机械操作装置如图所示,图中的尺寸单位为 mm 。
其操作臂由两根无缝 钢管所组成。
外伸端装有夹具,夹具与所夹持钢料的总重 F P =2200 N ,平均分配到两根钢管上。
求:梁内最大正应力(不考虑钢管自重)。
3习题 7-6 图解:1. 计算最大弯矩:−3 3M max = −2200N × 2395 ×10 m= −5.269 ×10 N ⋅ m2. 确定最大正应力:σ = M max = M max, α = 66mm = 0.611 max 32Wσ = M max =2 × πD 32 (1 −α 4 )5.268 N ⋅ m108mm = 24.71×106 Pa=24.71 MPa max2W =π (1= 08 ×10−3 m ) 2 × (1 − 0.6114 ) 327-7 图示矩形截面简支梁,承受均布载荷 q 作用。
若已知 q =2 kN/m ,l =3 m ,h =2b=240 mm 。
试求:截面竖放(图 c)和横放(图 b)时梁内的最大正应力,并加以比较。
习题 7-7 图解:1.计算最大弯矩:ql 22 ×103N/m ×(3m )2M max = = = 2.25 ×103 N ⋅ m8 82.确定最大正应力: 3平放: σ= M max = 2.25 ×10 N ⋅ m × 6= 3.91×106 Pa=3.91 MPamax 2−3 −3 2hb 6240 ×10 m ×(120 ×10 m)4⎝⎠竖放:σ= M max = 2.25 ×103 N ⋅ m ×6=1.95 ×106 Pa=1.95 MPamax2−3 −3 2bh 6120 ×10 m ×(240 ×10 m )3.比较平放与竖放时的最大正应力:σmax (平放) σmax (竖放) 3.91 1.95≈ 2.07-8 圆截面外伸梁,其外伸部分是空心的,梁的受力与尺寸如图所示。
图中尺寸单位为 mm 。
已知 F P =10kN ,q =5kN/m ,许用应力 [σ ]=140 MPa ,试校核梁的强度。
M解:画弯矩图如图所示:习题 7-8 图3σ ( ) Mmax1 = 32 ×30.65 ×10 N ⋅ m = 113.8 ×106 Pa=113.8 MPa< [σ ] max 实= W 1π (140 ×10-3m )3σ ( ) M max2 = 32 × 20 ×103 N ⋅ m = 100.3 ×106 Pa=100.3 MPa< [σ ] max 空= ⎡ ⎛ ⎞ ⎤W 2 π (140 ×10-3m )3 ⎢1 −⎢⎣ 100⎜140 ⎟ ⎥ 所以,梁的强度是安全的。
7-9 悬臂梁 AB 受力如图所示,其中 F P =10 kN ,M =70 kN ·m ,a =3 m 。
梁横截面的形状及尺寸均示于图中(单位为 mm),C 为截面形心,截面对中性轴的惯性矩 I z =1.02×108 mm 4,拉伸许用应力 [σ ]+=40 MPa , 压缩许用应力 [σ ]-=120 MPa 。
试校核梁的强度是否安全。
解:画弯矩图如图所示:σ σ σ σM (kN.m)C 截面习题 7-9 图3 −3+ max = 30 ×10 N ⋅ m ×96.4 ×10 m = 28.35 ×106Pa=28.35 MPa 1.02 ×108 ×10−12 m 43 −3D 截面- max = 30 ×10 N ⋅ m ×153.6 ×10 m = 45.17 ×106 Pa=45.17 MPa 1.02 ×108 ×10−12 m 43 −3+max = 40 ×10 N ⋅m ×153.6 ×10 m = 60.24 ×106 Pa=60.24 MPa> [σ ] 1.02 ×108 ×10−12 m 43 −3- max = 40 ×10 N ⋅ m ×96.4 ×10 m = 37.8 ×106 Pa=37.8 MPa 1.02 ×108 ×10−12 m 4所以,梁的强度不安全。
7-10 由 No.10 号工字钢制成的 ABD 梁,左端 A 处为固定铰链支座,B 点处用铰链与钢 制圆截面杆 BC 连接,BC 杆在 C 处用铰链悬挂。
已知圆截面杆直径 d =20 mm ,梁和杆的许用 应力均为 [σ ]=160 MPa ,试求:结构的许用均布载荷集度 [q ]。
Mmax P习题 7-10 图解:画弯矩图如图所示:对于梁:M max = 0.5qσ = M max ≤ [σ ], 0.5q ≤ [σ ] maxW W [σ ]W 160 ×106 × 49 ×10−6q ≤ = = 15.68 ×103 N/m=15.68 kN/m0.5 0.5对于杆:σ = F N ≤ [σ ],4F B = 4 × 2.25q ≤ [σ ] maxA πd 2 πd 2πd 2×[σ ] π ×(20 ×10-3 )2×160 ×106 q ≤== 22.34 ×103 N/m=22.34 kN/m4 × 2.254 × 2.25所以结构的许可载荷为[q ]= 15.68 kN/m7-11 图示外伸梁承受集中载荷 F P 作用,尺寸如图所示。
已知 F P =20 kN ,许用应力 [σ ]=160 MPa ,试选择工字钢的号码。
习题 7-11 图解:M = F ×1m=20×103 N ×1m=20 ×103 N ⋅ mσmax = M max W ≤ [σ ],F ×1m 20 ×103 ×1m W ≥ P= = 0.125 ×10-3 m 3=125 cm 3[σ ] 所以,选择 No.16 工字钢。
160 ×106Pa7-12 图示之 AB 为简支梁,当载荷 F P 直接作用在梁的跨度中点时,梁内最大弯曲正应 力超过许用应力 30%。
为减小 AB 梁内的最大正应力,在 AB 梁配置一辅助梁 CD ,CD 也可以看作是简支梁。
试求辅助梁的长度 a 。
解: 1.没有辅助梁时σmax= M max ≤ [σ ], W F P l 4 = 1.30 [σ ] Wσmax = Mmax ≤ [σ ], W F P l(3 − 2a ) 2 = [σ ] W F P l (3 − 2a ) F P l2 = 4 = [σ ] W 1.30 ×W 1.30 ×(3 − 2a ) = 3 a = 1.384 m7-13 一跳板左端铰接,中间为可移动支承。
为使体重不同的跳水者站在跳板前端在跳板中所产生的最大弯矩M zmax 均相同,问距离 a 应怎样变化?习题 7-13 图解:最大弯矩发生在可移动简支点B 处。