9矿井通风网络解算 (1)资料

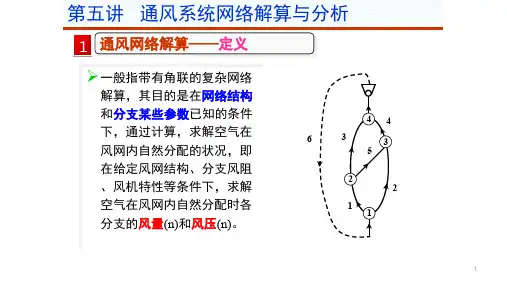
矿井通风网络解算基本算法之迭代法（Hardy-Cross）1. 矿井通风网络风量分配及复杂通风网路解算1.1 风量分配的基本定律风流在通风网路中流动时，都遵守风量平衡定律、风压平衡定律和阻力定律。

它们反映了通风网路中三个最主要通风参数——风量、风压和风阻间的相互关系，是复杂通风网路解算的理论基础。

1）通风阻力定律井巷中的正常风流一般均为紊流。

因此，通风网路中各分支都遵守紊流通风阻力定律，即（1）2）风量平衡定律风量平衡定律是指在通风网路中，流入与流出某节点或闭合回路的各分支的风量的代数和等于零，即（2）若对流入的风量取正值，则流出的风量取负值。

如图1（a）所示，节点⑥处的风量平衡方程为：如图1（b）所示，回路②-④-⑤-⑦-②的风量平衡方程为：图1 节点和闭合回路3）风压平衡定律风压平衡定律是指在通风网路的任一闭合回路中，各分支的风压（或阻力）的代数和等于零，即（3）若回路中顺时针流向的分支风压取正值，则逆时针流向的分支风压取负值。

如图1（b）中的回路②-④-⑤-⑦-②，有：当闭合回路中有通风机风压和自然风压作用时，各分支的风压代数和等于该回路中通风机风压与自然风压的代数和，即（4）式中，和分别为通风机风压和自然风压，其正负号取法与分支风压的正负号取法相同。

1.2 解算复杂通风网路的方法复杂通风网路是由众多分支组成的包含串、并、角联在内结构复杂的网路。

其各分支风量分配难以直接求解。

通过运用风量分配的基本定律建立数学方程式，然后用不同的数学手段，可求解出网路内各分支自然分配的风量。

这种以网路结构和分支风阻为条件，求解网路内风量自然分配的过程，称为通风网路解算，也称为自然分风计算。

目前解算通风网路使用较广泛的是回路法，即首先根据风量平衡定律假定初始风量，由回路风压平衡定律推导出风量修正计算式，逐步对风量进行校正，直至风压逐渐平衡，风量接近真值。

下面主要介绍回路法中使用最多的斯考德–恒斯雷法(Hard.Crross算法)。

矿井通风网络的解算摘要：矿井通风是矿山生产的重要环节之一。

安全、可靠、经济、实用的矿井通风系统对保证井下安全生产具有重要的意义。

随着计算机技术的飞速发展，现有的通风软件存在功能比较单一，针对这种情况，本文以Visual C++6.0为开发工具、SQL Server2000为后台数据库，进行了矿井通风网络解算的研究。

关键词：通风系统，网络解算1.引言矿井通风是矿山生产的一个重要环节。

安全、可靠、经济、实用的矿井通风系统，对保证井下安全生产具有重要意义。

煤矿生产过程的瓦斯爆炸、煤尘爆炸、矿井火灾、有毒气体窒息等灾害的发生都与矿井通风有直接关系[1]。

可以说通风状况的好坏直接影响工人的安全、健康和劳动效率，直接关系到煤矿的安全生产、经济效益和可持续发展。

随着煤矿产量增加，开采深度加大和机械化程度提高，需要加大风量，形成多进风井、多回风井的复杂通风系统。

如果矿井通风管理跟不上，事故隐患不能及时发现，矿井通风安全事故将会不断发生。

不但严重危害职工的健康和生命安全，而且破坏正常的通风系统，使安全生产无法正常进行。

因此，开展矿井通风网络解算、调节与评价的一体化系统研究，对保障矿井安全生产具有十分重要的理论意义和应用价值。

2.矿井通风网络的建模研究2.1流体网络建模数学模型是程序算法设计的灵魂。

能否选取恰当的方法，并建立起准确而全面的数学模型，是软件设计成功与否的决定性因素。

①数学模型对复杂的对象或系统进行计算或仿真时，首先要建立它的数学模型。

所谓数学模型就是由一系列数学方程(包括代数方程、微分方程)描述系统的每一个具体过程，最终组成一个联立方程组。

数学模型比较抽象，但它可以比较全面地反映一个复杂系统的性质。

当对一个系统的内部机理比较清楚时，就可以利用数学模型对其进行进一步的研究。

数学模型又可分为静态数学模型和动态数学模型。

②静态数学模型静态数学模型用来描述系统在稳定状态或平衡状态下各种输入变量与输出变量之间的关系。

第三章矿井通风网络理论与算法3.1矿井通风网络分析概述3.1.1矿井通风网络分析的目的和内容目的：主要是研究通风网络中个参数之间的相互关系（如h，Q，R等），各参数在特定的条件下的分布和变化规律，寻求解决通风实际问题的方法。

内容：最基本的内容可归纳为两个方面：一是网络解算（自然分风解算）。

二是网络调节（按需分风），取最优化调节方案。

3.1.2通风网络分析的方法主要有三大类：（1）图解法：是网络分析最早使用的方法（国内学者：唐海清、宋化沂、王冶、杨运良等，如平煤一矿网络的结算）。

（2）模拟法：电模拟、水模拟，五十年代比较流行，现已淘汰。

（3）数学分析法：是最早、最流行的方法之一。

对于一个矿井通风网络，根据风量、风压平衡定律，可列出一个足够数量的方程组来求解各巷道的风量。

但由于矿井中网络一般都比较复杂，因此列出的方程数量多，且为非线性，一般难以直接求出解析解。

如单角联这样的简单网络，就无法用一个公式来求出精确解。

因此，网络解算都采用数值分析方法---风量逐渐平衡试算法（渐近试算法，即斯考德-恒思雷法），需要列表进行大量繁杂的数值计算。

七十年代后，随着电子计算机的广泛应用，大量繁杂的数值计算可由计算机快速完成，这使得矿井通风网络分析的数值分析法得到了迅速的发展。

3.1.3通风网络分析的原则在应用矿井通风网络理论去分析和解决通风的实际问题，制定通风方案时要从通风网络结构的合理布局，通风设施的合理设置等多方面进行全面地考虑，以实现矿井通风的安全可靠、风流稳定、风速适宜（舒适）、经济合理。

（1）全局观点：矿井通风网络是一个有机的整体，各参数之间相互联系。

一是在选取分析对象时应把整个矿井作为一个整体来分析，而不应只对某个区域进行孤立的分析。

二是在分析评价一个通风方案的好坏时，要从系统全局出发去考虑。

（2）长远观点：矿井通风系统随着生产的发展而不断变化着，因此在考虑通风问题的解决方案时，应首先考虑长远计划，根据长远计划来选择解决当前问题的最佳方案。

第三节矿井火灾时期的风流控制矿井火灾时期的风流状态模拟的目的是正确的控制风流，以保证井下人员的安全撤离及救灾人员的安全工作，防止火灾事故的扩大，并有利于灭火工作的进行。

矿井火灾时期通风系统风流的控制的实质是：确定应施加于通风系统的各种控制的方式,位置和数量，以使通风系统的风流状态由某个已知的初态，在一定的时间内转移到所希望的某种状态。

这属于控制论中的大系统最优控制问题。

这一课题比火灾通风模拟更加复杂，目前仍处于研究初级阶段。

本节仅以对火灾通风模拟结果分析的角度，简述火灾时期风流控制的一些基本问题。

一、火灾时期受灾区域的确定矿井发生火灾后，矿井各部分的风流都将不同程度的受到影响，但通常所说的受灾区域主要是指火灾和烟流蔓延所及的区域。

火灾时期风流控制的一条重要原则就是尽量减少受灾区域的范围。

在实际发生火灾的矿井，目前一般是通过人员的实地侦查和监测系统的检测来确定受灾区域，这样往往只能是被动的了解已发生的情况。

当采用计算机对火灾时期的通风状态进行动态模拟时，可以迅速模拟得到火灾发生后不同时刻烟流在通风望网络中的蔓延状态。

结合图形显示输出，在通风系统图或网络图上采用不同颜色和线型可以表示出不同的烟流程度。

这样可以直观的看出矿井的受灾区域。

通过数值模拟还可以对烟流蔓延的趋势作出超前估计。

这对于正确选择遇险人员的撤离路线是非常重要的。

在矿井发生火灾后，针对具体情况，通过采取风流短路，局部减风或反风，防止角联分支风流反向，全矿反风等措施，疏导烟流和改变烟流蔓延路径，可以缩小烟流的蔓延范围，减少受灾区域范围或降低烟流蔓延的速度，为救灾赢得时间。

二火灾时期风流控制的基本要求和原则1 火灾时期风流控制的基本要求（1）保证矿井受灾区域内人员的安全撤离；（2）防止火灾的扩大，尽可能限制烟流在通风网络中的蔓延范围；（3）避免火灾气体或瓦斯达到爆炸危险的浓度；（4）有利于灭火和减少灾害损失。

2 火灾时期风流控制的一般原则（1）在火情不明或一时难于确定较好风流控制措施时，应首先保证矿井的正常通风，稳定风流方向，切忌随意调控风流；（2）发生火灾的分支，在确保可燃气体，瓦斯和煤尘不发生爆炸的前提下，应尽可能减少供风，以减弱火势和有利于灭火和封闭火区；（3）处于火源下风侧，并连接着工作地点或进风系统的角联分支，应保证其风向与烟流流向相反，以防烟流蔓延范围扩大；（4）处于烟流路线上，直接与总回风相连的风量调节分支，应打开其调节风门使风流段度，直接将烟流导入总回风中；（5）在矿井进风系统中发生火灾时，应进行全矿性反风。

矿井通风网络技术参照课本第五章内容第一节通风网络及矿井通风网络图一、矿井通风网络与网络图(一）矿井通风网络矿井开采中的图纸：采掘工程平面图、矿井通风系统图、矿井通风网络图。

矿井通风系统：是由通风机和通风网络两部分组成。

风流由入风井口进入矿井后，经过井下各用风场所，然后进入回风井，由回风井排出矿井，风流所经过的整个路线称为矿井通风系统。

用图论的方法对通风系统进行抽象描述，把通风系统变成一个由线、点及其属性组成的系统，称为通风网络。

１．分支（边、弧）分支是指表示一段通风井巷的有向线段，线段的方向代表井巷风流的方向。

每条分支可有一个编号，称为分支号。

如图中的每一条线段就代表一条分支。

用井巷的通风参数如风阻、风量和风压等，可对分支赋权。

不表示实际井巷的分支，如图中的连接进、回风井口的地面大气分支8，可用虚线表示(亦称为假分支)。

3. 路（通路、道路）是由若干条方向相同的分支首尾相连而成的线路。

如图中，1－2－5、1－2－4－6和1－3－6等均是通路。

6．独立回路由通风网络图的一棵树的若干条树枝及其余树中的一条余树枝形成的回路，称为独立回路。

如图（a）中的树与余树枝5、2、3可组成的三个独立回路分别是：5-6-4、2-4-6-7-8-1和3-6-7-8-1。

（1）树枝数为m-1，加上余树枝j等于风网中的分支数n，即n=m-1+j，j=n-m+1。

一个节点数为m，分支数为n的通风网路的余树枝数为n－m＋1。

（2）由n－m＋1条余树枝可形成n－m＋1个独立回路。

（二）矿井通风网络图矿井通风网络图：用直观的几何图形来表示的通风网络。

1. 特点：１）通风网络图只反映风流方向及节点与分支间的相互关系，节点位置与分支线的形状可以任意改变。

２）能清楚地反映风流的方向和分合关系，并且是进行各种通风计算的基础，因此是矿井通风管理的一种重要图件。

网络图两种类型：一种是与通风系统图形状基本一致的网络图；另一种是曲线形状的网络图。

第五章矿井通风网络中风量分配与调节本章主要内容及重点和难点1、风量分配基本定律----三大定律2、网络图及网络特性1)简单网络2)角联及复杂网络3、网络的动态分析4、矿井风量调节5、计算机解算复杂网络矿井通风系统是由纵横交错的井巷构成的一个复杂系统。

用图论的方法对通风系统进行抽象描述，把通风系统变成一个由线、点及其属性组成的系统，称为通风网络。

第一节风量分配基本规律一、矿井通风网络与网络图(一）矿井通风网络通风网络图：用直观的几何图形来表示通风网络。

1. 分支（边、弧）：表示一段通风井巷的有向线段，线段的方向代表井巷中的风流方向。

每条分支可有一个编号，称为分支号。

2. 节点（结点、顶点）：是两条或两条以上分支的交点。

3. 路（通路、道路）：是由若干条方向相同的分支首尾相连而成的线路。

如图中，1－2－5、1－2－4－6和1－3－6等均是通路。

4. 回路：由两条或两条以上分支首尾相连形成的闭合线路称为回路。

如图中，2－4－3、2－5－6－3和1－3－6－75、树：是指任意两节点间至少存在一条通路但不含回路的一类特殊图。

由于这类图的几何形状与树相似，故得名。

树中的分支称为树枝。

包含通风网络的全部节点的树称为其生成树，简称树。

（二）矿井通风网络图特点：1）通风网络图只反映风流方向及节点与分支间的相互关系，节点位置与分支线的形状可以任意改变。

2）能清楚地反映风流的方向和分合关系，并且是进行各种通风计算的基础，因此是矿井通风管理的一种重要图件。

网络图两种类型：一种是与通风系统图形状基本一致的网络图，如图5-1-3所示；另一种是曲线形状的网络图，如图5-1-4所示。

但一般常用曲线网络图。

绘制步骤：(1) 节点编号在通风系统图上给井巷的交汇点标上特定的节点号。

(2) 绘制草图在图纸上画出节点符号，并用单线条（直线或弧线）连接有风流连通的节点。

(3) 图形整理按照正确、美观的原则对网络图进行修改。

通风网络图的绘制原则：(1) 用风地点并排布置在网络图中部，进风节点位于其下边；回风节点在网络图的上部，风机出口节点在最上部；(2)分支方向基本都应由下至上；(3) 分支间的交叉尽可能少；(4) 网络图总的形状基本为“椭圆”形。

3.6 矿井通风网络解算的计算方法3.6.1算法概述3.6.1.1通风网络解算的内容通风网络解算就是在已知通风网络中的几何结构（网络图）、各分支风阻、各风机特性曲线、矿井的自然风压等基础数据的情况下，要求：（1） 计算网络中各分支的风量和阻力；（2） 计算各扇风机在该网络上工作时的工况参数。

除了计算矿井在设计和正常生产情况下的通风状况外，还可计算出矿井在冒顶、火灾、风机故障等非正常情况下和各种可预见的情况（如工作面贯通、采完封闭等）下网络的通风状况。

但不论在什么情况下，所计算的都是空气在网络中自然流动状况，所以矿井通风网络解算又称为自然分风计算。

3.6.1.2网络自然分风计算的数学模型在3.5节中已经给出了用不同形式描述的风压、风量平衡定律，它们是任何矿井通风网络分析问题的基本数学模型。

风量平衡定律：01=∙∑=nj j ijq b（i=1,2,3,…,m-1），BQ=0 （3-10）风压平衡定律：01=∑=nj ij i h c（i=1,2,3,…,b ） ，CH=0 （3-15）通风网络解算的目的就是要计算出同时满足以上两式的一组风量和一组风压：T Q =（q 1，q 2，q 3，…，q n ，） T H =（h 1，h 2，h 3，…，h n ，） 式（3-10）有m-1个独立风量方程，式（3-15）有n-m+1个独立风压方程式，两式联立有：独立方程数：（m-1）+(n-m+1)=n 个；又知在n 个未知风量中，只有n-m+1个是独立的。

在n 个未知风压中，只有m-1个是独立的。

因此：独立变量数：(n-m+1)+（m-1）=n 个所以两式联立后，独立方程数正好等于独立变量数，故方程组是有解的。

因在式（3-15）中j N j f j j j j h h h q r h --∆+=2，所以，所得方程组是非线性的。

对这样一个非线性方程组，一般均无法直接用解析法求解（除简单并联外）。

因而只能用数值解法求其数值解。

教学模块Ⅲ通风网络图及风量分配3.1 矿井通风网络中风流基本规律与风量分配矿井通风系统是由纵横交错的井巷构成的一个复杂系统。

由若干风道和交汇点构成的通风系统，是由线、点及其属性组成的，称为通风网络。

通风系统中各井巷分配的风量大小及其方向遵循一定规律。

在全矿井的风网中风量分配有两种，一是按需分配，二是自然分配。

前一种是根据井下各个用风地点的实际需要进行分配的方法，为了保证这种分配，必须采取一系列的控制措施，井下大部分网络中的风量是用这种方法进行分配的。

后一种是取决于通风网络中各网络的风阻比例关系，不加控制任风量自然地进行分配的方法，这种分配方法多半用于矿井的进风和回风通风网络中，但必须在保证井下各个用风地点实现按需分配风量的前提下进行。

3.1.1 风网的基本术语和形式3.1.1.1 通风网络的基本术语矿井通风网络：用直观的几何图形来表示通风网络就得到通风网络图。

对通风网络进行分析时，常用到以下一些术语：1．节点是指两条或两条以上分支的交点。

每个节点有惟一的编号，断面或支护方式不同的两条风道，其分界点有时也可称为节点。

2．分支(边、弧) 是两节点间的连线，在通风网络图上，每条分支可有一个编号，称为分支号，用单线表示分支。

其方向即为风流的方向，用箭头表示，箭头自始节点指向末节点。

若分支并不表示实际井巷，如连接进、回风井口的地面大气分支，则称为伪分支，常用虚线表示，由扇风机出口到进风井口的一段a—a。

3．路(通路) 是由若干方向相同的分支首尾相接而成的线路，即某一分支的末节点是下一分支的始节点。

4．回路和网孔是由若干方向并不都相同的分支所构成的闭合线路，其中有分支者叫基本回路，简称回路，无分支者叫网孔。

5．生成树它包括通风网络中全部节点和不构成回路或网孔的一部分分支。

每一种通风网络都可选出若干生成树。

由于这类图的几何形状与树相似，故得名。

树中的分支称为树枝。

3.1.1.2 矿井通风网络图通风网络图只反映风流方向及节点与分支间的相互关系，节点位置与分支线的形状可以任意改变，因此网络图的形状可以千变万化。

第五章通风网路中风量的分配第一节通风网路及矿井通风网路图一、通风网路的基本术语和概念１．分支分支是指表示一段通风井巷的有向线段，线段的方向代表井巷风流的方向。

每条分支可有一个编号，称为分支号。

如图5-1中的每一条线段就代表一条分支。

用井巷的通风参数如风阻、风量和风压等，可对分支赋权。

不表示实际井巷的分支，如图5-1中的连接进、回风井口的地面大气分支8，可用虚线表示。

图5-1 简单通风网路图２．节点节点是指两条或两条以上分支的交点。

每个节点有唯一的编号，称为节点号。

在网路图中用圆圈加节点号表示节点，如图5-1 中的①～⑥均为节点。

３．回路由两条或两条以上分支首尾相连形成的闭合线路，称为回路。

单一一个回路（其中没有分支），该回路又称网孔。

如图5-1 中，1-2-5-7-8、2-5-6-3和4-5-6等都是回路，其中4-5-6是网孔，而2-5-6-3不是网孔，因为其回路中有分支4。

４．树由包含通风网路图的全部节点且任意两节点间至少有一条通路和不形成回路的部分分支构成的一类特殊图，称为树；由网路图余下的分支构成的图，称为余树。

如图5-2所示各图中的实线图和虚线图就分别表示图5-1的树和余树。

可见，由同一个网路图生成的树各不相同。

组成树的分支称为树枝，组成余树的分支称为余树枝。

一个节点数为m，分支数为n的通风网路的余树枝数为n －m＋1。

图5-2 树和余树５．独立回路由通风网路图的一棵树及其余树中的一条余树枝形成的回路，称为独立回路。

如图5-2（a）中的树与余树枝5、2、3可组成的三个独立回路分别是：5-6-4、2-4-6-7-8-1和3-6-7-8-1。

由n－m＋1条余树枝可形成n－m＋1个独立回路。

二、通风网路图的绘制不按比例、不反映空间关系的矿井通风网路图，能清楚地反映风流的方向和分合关系，便于进行通风网路解算和通风系统分析，是矿井通风管理的重要图件之一。

通风网路图的形状是可以变化的。

为了更清晰地表达通风系统中各井巷间的联接关系及其通风特点，通风网路图的节点可以移位，分支可以曲直伸缩。

1.1.1 概述矿井通风的主要任务是根据各用风地点的需要供给新鲜风流。

新风在被送到各用风地点直至排出地面要经过许多巷道，这些进回风巷与用风巷地点形成矿井通风系统，按矿井的风流方向，依次相联而成的网状线路叫做通风网路。

在进行通风管理及设计工作中或改善矿井通风系统时，往往要进行网路解算。

解算网路的原理是依据风量平衡定律、风压平衡定律、阻力定律及已知参数列出方程组（独立方程的个数要和独立未知数的个数相等），然后求解。

由于未知数的个数众多，阻力定律又是二次方程，利用代数法解算甚为困难。

1931年，H〃柴操德提出几何法计算θ型网路风量；1938年，S〃威克斯提出了简单网路图解法；50年代，W〃马斯等提出了电力模拟法解算复杂的通风网路，后来又经历了通风网路（迭代）试算法。

以后这种试算法在使用中不断完善，特别是六十年代应用数字电子计算机解算通风网路以来，复杂网路迭代试算法得到了迅速发展和广泛的使用。

解算复杂的通风网路的迭代试算法可分为两类：一类是回路法，即由假定回路内分支风向和风量开始，逐步修正，使之满足风压平衡定律；一类是节点法，由假定风流节点的压力值，逐步修正压力分布值，使之满足风量平衡定律。

1.1.2 软件简介目前我矿使用的矿井通风网络解算软件原名"风丸"（以下皆称之为风丸），是由日本九州大学工学研究院井上雅弘博士编制，编制的主要计算机语言为V-Basic,它的主要工作原理：利用风量平衡定律、风压平衡定律、阻力定律及已知参数进行模拟解算，首先给出网路中各个回路风量的近似值，使它们满足风量平衡定律，然后利用风压平衡定律对初拟的回路风量逐一进行修正，这样经过多次反复迭代计算、修正，使风压逐渐平衡，风量逐渐接近于真值。

1.2 风丸软件的界面1.2.1软件应用环境风丸软件支持Windows 98以上计算机操作系统，对计算机的内存、CPU、硬盘、CD-ROM、打印机无特殊要求。

1.2.2 安装启动计算机，进入windows98（或以上）操作系统，插入软盘（带风丸软件的），直接将其拷进硬盘某一目录下即可，或者直接在软盘中使用。

矿井通风网络解算算法及优化算法研究摘要：受到目前矿产资源开采深度的不断向着纵深化发展，矿井通风问题也便更为了一项亟须解决的现状问题，这对于矿井管理工作而言难度也更加巨大。

矿井通风系统数字化发展是解决目前深层矿井通风问题的一种主要解决措施，传统的通风软件在解决这一问题时通常所采取的是节点风压与回路风量两种方法，然而这两种方法均存在着一定的缺陷与不足，难以适应于当前复杂矿井通风系统的实际需求。

关键词：矿井通风；网络解算；网络模型；三维可视化0引言早在1936年时，Cross H就提出了流体网络分析方法，从此以后，科研工作人员利用数值计算的方式及图论理论来处理矿井自然分风问题。

这在一定程度上解决了矿井通风系统多态流动的分析问题，低速风流、采空区风流以及高速风流等可以进行混合运算，获取到的数值也更接近实际数值。

同时，明确了算法的收敛性条件及定理。

本文针对矿井通风智能化系统中存在的问题，给出了以下解决思路及方式。

1系统整体设计矿井通风的有效与否直接关系着矿井生产作业的安全程度，在开展矿井通风安全管理工作时其通常会牵涉到相关的采矿工程、测量学、数据库、计算机等多门专业学科领域知识，矿井通风系统最为显著的一项特点即为井下多处需风地物理空间间距大，信息数据规模总量大，通风网络构造与巷道通风参数存在着动态变化性的特征。

因而，矿井通风可视化系统也便有着多学科综合且专业性较强的特性[1]。

在开展三维可视化矿井通风网络系统设计时，具体可将其分为以下三大部分内容：1.1网络解算基于图高效遍历、节点风压法、回路风量法所构成的矿井通风优化调控系统。

1.2数据可视化表达基于网络拓扑、网络分支、网络节点、通风设备、通风构筑物、多边形区域三角化、多层轮廓线三维重建所构成的矿井通风属性数据模型。

1.3系统开发基于数字孪生软件平台、功能插件所构成的三维矿井通风仿真系统。

2通风网络模型与解算在整个矿井通风网络解算系统当中所应用的解算方法有着极其重要的作用价值，将直接关乎着所建设的模型是否可体现出风网拓扑关系、运动规律及风流方向等特征，稳定程度与收敛速度也是影响整体程序稳定性及整体效率最关键的内容之一。

矿井通风网络节点风压解算法及其ＱＢＡＳＩＣ程序设计李济吾（南方冶金学院－赣州３４１０００）周基校（柿竹园多金属矿・郴州４２３００，Ｊ）摘要文中介绍了矿升通风同络自然分风用节点风压法解算方法的数学模型、算法及骶图．用高级语言ＱＢＡＳＩＣ编制了计算程序．在５８６微机上调试通过，并经实倒运算正确。

应用ＱＢＡＳＩｒ．＂语言编制程序简单方便，界面友好，易于修改，通用性强。

所编程序简单实用，功能较强．易为广大通风Ｉｉ作者接受．时提高矿山通风管理水平有一定指导意义。

关键词矿井通风，通风网络解算，ＱＢＡＳＩＣ语言。

矿井通风网络自然分风解算的实质是给定风网、分支风阻和分支通风动力的前提下求解分支风量和分支通风阻力。

其解算方法可分为两大类：风量法及风压法。

具体解算方法有数十种之多。

本文介绍一种节点风压法解算自然分风的基本原理及其用ＱＢＡＳＩＣ语言编制程序。

１节点风压法数学模型节点风压法是以节点的全压能力为基本未知量的风网解算方法，即先求解节点风压为未知量的方程组，再由节点风压计算各分支风量和通风阻力。

对于Ｂ条分支，Ｎ个节点的风网，其数学模型为：Ｎ—ｌ∑ａｉｉＰ．＝ＲｊＱｊｌＱＪｌ—Ｈｏ—Ｉ｛ｑ（产１，２．……，Ｂ）（１）Ｂ∑８ｋ，Ｑ．＝０】２Ｊ（ｋ＝ｌ，２．－…・，Ｎ一１）（２）式中ａ。

一关联矩阵Ａ中的第ｉ行第ｊ列元素；Ｐ．一ｉ节点的压力，只；Ｈ¨Ｈ，一；分支通风动力、位压差，Ｐａ；Ｒ．、Ｑ．一Ｊ分支风阻及风量。

由式（１）和（２）联立的方程组有定解。

该方程组为非线性方程组，要进行迭代计算才能求解。

将（１）式写成以Ｐ．为因变量，Ｑ．为函数的显函数形式，并代入（２）式，最终得到以Ｐ．（ｉ＝ｌ，２，…，Ｎ一１）为未知量的Ｎ～１个独立方程，由此求解Ｐ．，然后就可计算出分支通风阻力和风量，达到解算风网的目的。

迭代计算的数值算法不同，将得到不同算法。

下面用牛顿法进行迭代计算。

２牛顿法数学原理由（１）式可得：Ｑ＝／ＩＨｎ十Ｈｑ＋∑ａｕＰｉｆ／Ｒ１＋ＳｎＥ（Ｈｆｉ＋Ｈｅｉ十∑ａ…Ｐ）（Ｂ）将式（３）在Ｑ，ｏ，Ｐ．ｏ（ｊ＿１，２，…，矿井通风网络节点风压解算法及其ＱＢＡＳＩＣ程序设计Ｂ；ｉ＝１，２。