下载文档原格式
..... . ... 时Sr诫呎------------- --- 培训游戏大全（团体游戏篇103个游戏）一.备受攻击目的：体验被排挤的滋味内容：1. 抽出一人做箭靶。
2•在地上画一个圆圈，或用绳圈也可，箭靶”站在中间，其他人要拍打他最少3次。
但不可给箭靶”碰到，被碰到的人便要做箭靶”了。
备注：如有8人以上，分为两组为佳，这可易于走动。
变化：箭靶”可拉人入圈（这个圈一定要大一点），帮他一起捉人，即圈内人越来越多，直至所有人都入了圈为止。
二.毕加索目的：考沟通能力时间：10~20分钟材料：笔和纸内容：1. 组长先预备数张画了圆形的纸。
最好有多张。
2. 每两人配对比赛。
3. 开始前，每一组合背对背而坐。
4. 在指定时间内，一人负责讲圆形，另一人则负责画圆。
画圆的人，只可听不可问，也不可让讲的人看到。
5. 时间到，就看谁画得快而准。
6. 也可对换角色。
备注：1. 这游戏可看到各人不同的沟通问题。
2. 组长可在游戏后，讲解沟通的艺术和重要。
三.各抒己见目的：了解组员的时事触角，学习直言表达时间：15分钟材料：当日报纸内容：组长说：今日是时事论坛，有个人意见要尽情表达。
”1•选数则有意义又富争论性的新闻，请大家表达看法。
了解各组员的分析力，个人观点、立场等'、、、、'2. 组长不会下结论，但要赞赏组员表达及互相尊重的态度。
------------------- 时磊5说------ ---- -------- 四.旁若无人目的：考验组员的分析力、观察力、最终带出旁若无人的坏处时间：15分钟内容：组长说一两个人在你面前讲暗语，对你视若无睹，你感觉如何？”1. 两人一组，秘密地在房中选一件物品作为讨论目标。
在众人面前讨论时，不可提示物件名称。
其他组员听后尝试寻找出答案。
2. 轮流讨论竟猜。
3. 完结时，组长要指出旁若无人的沟通方式，是令别人难受的五.波涛汹涌目的：让气球停留在空中，激发欢乐时间：5~10分钟材料：气球多个内容：组长说：如果你心中有气，顶在胸口会好辛苦，我们为别人赶走这气好吗？”1. 每人一个不同颜色的气球。
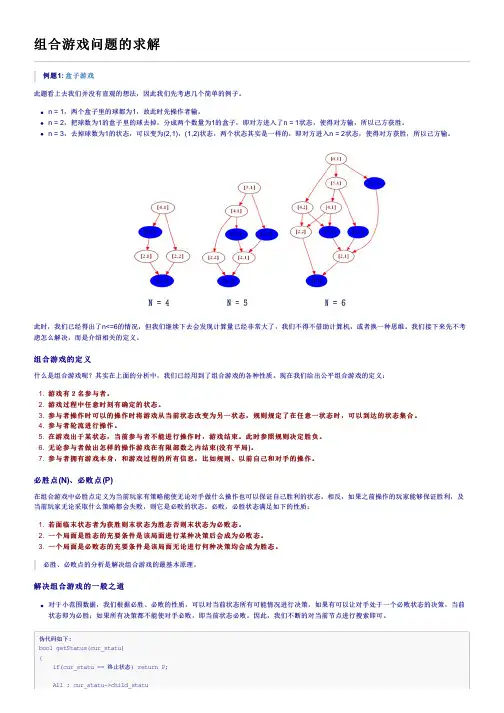
的状态，可以变为(2,1)，(1,2)状态，两个状态其实是一样的，即对方进入n = 2状态，使得对方获胜，所以己方输。
的情况，但我们继续下去会发现计算量已经非常大了，我们不得不借助计算机，或者换一种思维。
我们接下来先不考虑怎么解决，而是介绍相关的定义。
由下往上推，我们可以发现这么一个规律，终止节点sg = 0，终止节点为必败点，连接终止节点的点为必胜点，其。
于是乎，我们总结得出sg = 0的节点为必败点，sg > 0的点为必胜点。
证明也想当容易：
时，做任何一个决策，都会改变其中一个 sg 值，导致对应的二进制位发生变化，即会变成。
博弈论题⽬总结（三）——组合游戏进阶第⼆波题⽬⼤多都是sg组合游戏的基本变形，是对游戏规则的⼩改动。
容易提取出SG函数的模型，且SG函数的规律也⽐较简单⽽本⽂的题⽬需要较多的模型转化思想但博弈论的精髓还是打表翻硬币游戏⼀条直线上有很多硬币，有的正⾯朝上，有的反⾯朝上，每次可以翻⼀些硬币，但最右边的硬币必须由正变反，不能操作者输翻硬币可能会有奇奇怪怪的要求，⼀次翻好⼏个，⼀次翻连续的⼏个结论：正⾯朝上的⽯⼦之间互不影响，设正⾯朝上是1，反⾯朝上是0，那么SG(0101001)=SG(01)^SG(0001)^SG(0000001)证明见论⽂树形删边游戏SG(u)=xor{SG(v)+1}证明见jzh神犇的论⽂POJ 3710 Christmas Game环怎么处理啊？⼀个奇环可以分成等长的两条链，SG函数值为0，其他后继状态的SG函数值均>1，故奇环的SG函数值为1⼀个偶环只能分成异奇偶的两条链，SG函数值均>0，故奇环的SG函数值为0tarjan边双缩点搞⼀下就⾏了1 #include <cmath>2 #include <cstdio>3 #include <cstring>4 #include <algorithm>5#define N1 1056#define M1 5057#define ll long long8#define dd double9using namespace std;10const dd eps=1e-7;1112 template <typename _T> void read(_T &ret)13 {14 ret=0; _T fh=1; char c=getchar();15while(c<'0'||c>'9'){ if(c=='-') fh=-1; c=getchar(); }16while(c>='0'&&c<='9'){ ret=ret*10+c-'0'; c=getchar(); }17 ret=ret*fh;18 }19struct Edge{20int to[M1*2],nxt[M1*2],val[M1*2],head[N1],cte;21void ae(int u,int v,int w)22 {23 cte++; to[cte]=v; nxt[cte]=head[u];24 head[u]=cte; val[cte]=w;25 }26 }e,E;2728int T,n,m;29int low[N1],dfn[N1],use[N1],stk[N1],dad[N1],sum[N1],tim,num,tp;30void tarjan(int x,int fa)31 {32int j,v;33 low[x]=dfn[x]=++tim; stk[++tp]=x; use[x]=1;34for(j=e.head[x];j;j=e.nxt[j])35 {36 v=e.to[j]; if(e.val[j]==fa) continue;37if(!dfn[v]){38 tarjan(v,e.val[j]);39 low[x]=min(low[x],low[v]);40 }else if(use[x]){41 low[x]=min(low[x],dfn[v]);42 }43 }44if(low[x]==dfn[x])45 {46 num++;47while(stk[tp]!=x){ use[stk[tp]]=0; dad[stk[tp]]=num; sum[num]++; tp--; }48 use[x]=0; dad[x]=num; sum[num]++; tp--;49 }50 }5152void rebuild()53 {54int i,j,v;55for(i=1;i<=n;i++)56 {57for(j=e.head[i];j;j=e.nxt[j])58 {59 v=e.to[j];60if(dad[i]!=dad[v])61 E.ae(dad[i],dad[v],0);62 }63 }64 }6566int sg[N1],de;67void dfs(int x,int fa)68 {69int j,v;70for(j=E.head[x];j;j=E.nxt[j])71 {72 v=E.to[j]; if(v==fa) continue;73 dfs(v,x); sg[x]^=sg[v]+1;74 }75if(sum[x]>1 && (sum[x]&1)) sg[x]^=1;76 }7778void init()79 {80 memset(sg,0,sizeof(sg)); memset(low,0,sizeof(low));81 memset(sum,0,sizeof(sum)); memset(dfn,0,sizeof(dfn));82 memset(dad,0,sizeof(dad)); memset(use,0,sizeof(use));83 memset(&e,0,sizeof(e)); memset(&E,0,sizeof(E));84 tim=0; tp=0; num=0;85 }8687int N;88int main()89 {90int i,j,x,y;91while(scanf("%d",&N)!=EOF) {9293int ans=0;94while(N--)95 {96 init(); read(n); read(m);97for(i=1;i<=m;i++)98 {99 read(x); read(y); e.ae(x,y,i); e.ae(y,x,i);100 }101for(i=1;i<=n;i++) if(!dfn[i]) tarjan(i,-1);102 rebuild();103 dfs(dad[1],-1);104 ans^=sg[dad[1]];105 }106if(ans) puts("Sally"); else puts("Harry");107108 }109return0;110 }View CodeK倍动态减法游戏现在有⼀堆⽯⼦，两个⼈轮流取，后⼿取的⽯⼦数不能超过先⼿取的K倍，第⼀个⼈不能⼀下⼦把⽯⼦都取完，取最后⼀个⽯⼦的⼈赢，问谁能赢在探究“K倍动态减法游戏前”，先研究⼀下2倍动态减法游戏，即fibonacci博弈2倍动态减法游戏结论：当剩余⽯⼦数是斐波那契数时，先⼿必败简单证明如下⽯⼦数为2,3时，显然先⼿必败。
算法合集之《组合游戏略述——浅谈SG游戏的若干拓展及变形》组合游戏是一种数学游戏，它可以用来解决多个独立游戏的组合问题。
其中，SG游戏是一种特殊的组合游戏，它的规则比较简单，每一步可以选择一个盒子，然后将里面的石子取出，在该盒子里面放入石子，并将该盒子放入另一个没有被选中的盒子中。
游戏的目标是使对手无法进行有效的操作，即游戏状态无法转移到一个必败状态。
在这篇文章中，我们将讨论SG游戏的一些拓展及变形。
首先是SG游戏的拓展。
在原始的SG游戏中，只有两个玩家进行游戏。
但是，在实际应用中，有时候会需要更多的玩家参与游戏。
为了适应这种情况，可以将SG游戏扩展到多人版本。
例如，可以在游戏的每一步中，每个玩家选择一个盒子，并进行相应的操作。
这样，每个玩家都需要考虑其他玩家的策略，以及如何最大化自己的利益。
这种多人SG游戏的策略分析更加复杂，但也更加有趣。
其次是SG游戏的变形。
SG游戏中的石子数量是固定的，但是在实际应用中，可能会出现不同的石子数量。
例如，可以将每个盒子中的石子数量设置为随机数，或者是一个特定的数值。
这样，玩家在进行游戏时，需要考虑不同石子数量的影响，并调整自己的策略。
另外，可以考虑加入其他的游戏元素，例如限制玩家的操作次数或规定特殊的操作规则。
这些变形可以增加游戏的难度和趣味性。
最后，我们来讨论SG游戏的求解方法。
在SG游戏中，每一种游戏状态都可以用一个非负整数来表示，这个整数被称为SG函数值。
通过计算SG函数值，可以判断一个游戏状态是否为必胜状态。
基本的求解方法是递归算法。
首先，定义SG函数值为0的状态为必败状态，然后逐步求解其他状态的SG函数值。
具体的方法是，先计算所有可以转移到其他状态的状态的SG函数值，然后根据转移关系求出当前状态的SG函数值。
最后，根据SG函数值的计算结果判断游戏状态是否为必胜状态。
综上所述，SG游戏是一种有趣的组合游戏，通过拓展和变形可以增加游戏的难度和趣味性。
使用递归算法可以求解SG游戏的必胜状态。
博弈论基础之sg函数与nim 在算法竞赛中，博弈论题⽬往往是以icg。
通俗的说就是两⼈交替操作，每步都各⾃合法，合法性与选⼿⽆关，只与游戏有关。
往往我们需要求解在某⼀个游戏或⼏个游戏中的某个状态下，先⼿或后⼿谁会胜利的问题。
就⽐如经典的：⼏堆⽯⼦，两⼈可以分别拿若⼲个，⼀次只能选择⼀个⽯⼦堆操作，问给定状态下，先⼿胜利还是后⼿胜利？ ⽽nim与sg函数就是对于这类问题的解法，在我的理解看来，sg函数和nim分别对应不同阶段的决策：前者对于单个游戏决策，后着是将这些单个游戏综合起来的整体决策。
⼀、状态与转移 icg游戏往往可以分为两个部分，规则与局⾯。
⽽这两个分别对应了转移与状态。
规则决定了状态转移的合法性，状态是转移的基本。
什么是状态？状态是⼀个静态的局⾯。
就好⽐当下棋时的局⾯⼀样。
在游戏的每个阶段，不论是开始，中间，或是结束。
每⼀个局⾯都对应了⼀种状态。
什么是状态的转移？单个分开的局⾯⽆法构成⼀个完整的游戏，所以就需要从某⼀个状态转移到另⼀个状态，来进⾏⼀次操作。
举个例⼦：有5个⽯⼦放在⼀堆。
5个⽯⼦就是⼀种状态，在不受限制下，你可以改变这个状态。
例如：取⾛4个⽯⼦。
就是将5个⽯⼦这个状态转移到1个⽯⼦这个状态，操作就是取⾛4个⽯⼦。
⽽这个操作的合法性取决于游戏的规则。
例如：⼀次最多取3个⽯⼦。
那么上条操作取4个⽯⼦就是⼀次不合法的操作，意味着你不能从5这个状态直接转移到1这个状态。
那么对于5个⽯⼦，每次最多取三个，从中我们可以得到如下状态转移的图（有向）⼆、sg函数 概念 ⾸先，引⼊mex值的概念。
mex是指不属于集合中整数的最⼩正整数。
⽽sg值就是不属于后继集合的最⼩正整数。
例如上图中：0没有后继元素所以最⼩正整数为0，sg(0)=0； 1后继元素只有0，不属于后继集合的最⼩正整数为1，sg(1)=1; 同理可得sg(2)=2;sg(3)=3; 到4的时候，情况就发⽣了变化。
SG函数给定一个有向无环图和一个起始顶点上的一枚棋子，两名选手交替的将这枚棋子沿有向边进行移动，无法移动者判负。
事实上，这个游戏可以认为是所有Impartial Combinatorial Games的抽象模型。
也就是说，任何一个ICG都可以通过把每个局面看成一个顶点，对每个局面和它的子局面连一条有向边来抽象成这个“有向图游戏”。
下面我们就在有向无环图的顶点上定义Sprague-Garundy函数。
首先定义mex(minimal excludant)运算，这是施加于一个集合的运算，表示最小的不属于这个集合的非负整数。
例如mex{0,1,2,4}=3、mex{2,3,5}=0、mex{}=0。
对于一个给定的有向无环图，定义关于图的每个顶点的Sprague-Gar undy函数g如下：g(x)=mex{ g(y) | y是x的后继}。
来看一下SG函数的性质。
首先，所有的terminal position(终端态)所对应的顶点，也就是没有出边的顶点，其SG值为0，因为它的后继集合是空集。
然后对于一个g(x)=0的顶点x，它的所有后继y都满足g(y)!=0。
对于一个g(x)!=0的顶点，必定存在一个后继y满足g(y)=0。
以上这三句话表明，顶点x所代表的postion是P-position当且仅当g (x)=0（跟P-positioin/N-position的定义的那三句话是完全对应的）。
我们通过计算有向无环图的每个顶点的SG值，就可以对每种局面找到必胜策略了。
但SG函数的用途远没有这样简单。
如果将有向图游戏变复杂一点，比如说，有向图上并不是只有一枚棋子，而是有n枚棋子，每次可以任选一颗进行移动，这时，怎样找到必胜策略呢？让我们再来考虑一下顶点的SG值的意义。
当g(x)=k时，表明对于任意一个0<=i<k，都存在x的一个后继y满足g(y)=i。
也就是说，当某枚棋子的SG值是k时，我们可以把它变成0、变成1、……、变成k-1，但绝对不能保持k不变。
